基于支持向量机的设备故障诊断研究

刘一鸥

（西安外事学院 陕西 西安710077）

基于支持向量机的设备故障诊断研究

刘一鸥

（西安外事学院 陕西 西安710077）

支持向量机作为基于统计学理论的机器学习方法，在人工智能识别方面的研究起到了重要的作用。本文将支持向量机智能识别方法引入到机械设备的故障诊断当中，并对支持向量机模型起到关键作用的惩罚因子c和核参数g采用了交叉验证的方法进行最优化计算。建立了基于优化的支持向量机的机械设备故障诊断模型，并且进行了相关实验，实验表明，采用本文介绍的基于支持向量机的故障诊断方法可有效识别出机械设备的故障类型，对机械设备的故障诊断提供了有效的诊断方法。

支持向量机；交叉验证；机械设备；故障诊断

机器学习是指这样的过程：通过对样本的训练，寻找输入变量和输出变量的关系的一种近似估计，这种估计得够以较高的准确率来预测输出变量的结果。目前，研究者们建立了各种诸如KNN（K最近邻）算法、神经网络算法以及支持向量机算法等等一系列基于向量空间模型的训练算法和分类算法[1-2]。其中支持向量机 （Support Vector Machine）是由研究专家Cortes和Vapnik首先发现并提出的，在小样本、非线性及高维模式识别等领域中表现了较好的应用优势，并且也能够在函数拟合等其他机器学习中发挥积极的作用[3]。如文献[4]通过对风机传动系统中齿轮故障进行模拟试验，构建结构风险最优的支持向量机（SVM）网络，采用SVM对齿轮箱试验台齿轮故障进行诊断分类识别，取得较好的效果，说明SVM作为一种故障诊断方法的实用性。文献[5]提出了一种基于支持向量机的矿井通风机故障诊断方法。并且证明了支持向量机对有限的样本数据具有良好的学习能力。可快速并准确地诊断矿井通风机故障的目的。文献[6]针对转子系统故障信息的复杂性，提出将小波包分析和支持向量机相结合的转子系统早期故障诊断方法。该方法首先利用改进的小波包方法提取早期故障特征；然后将提取的特征向量输入基于支持向量机的分类器进行故障识别。实验分析结果表明，该方法在小样本情况下，能够有效识别转子系统的早期故障，具有很好的分类精度，而且能够实现旋转机械的多故障诊断。通过文献可以看出，采用支持向量机的方法可以有效的进行机械设备的故障诊断，在运用SVM做分类预测时，需要针对惩罚参数c和核函数参数g等调节相关参数，才能使得分类预测的准确率较高。交叉验证CV，（Cross Validation）思想的运用在一定程度上能够获得最优的参数，从而在学习和欠学习状态等不同状态下获得准确率较好的测试结果。相关的研究证明，运用交叉验证选择参数进行SVM训练所得到的模型要优于随机选取参数，分类效果也更好。而交叉验证的方式是目前较为有效的进行惩罚因子c和核参数g求取方法，因此本文在前人研究的基础上采用交叉验证方法进行机械设备故障识别模型的最优化建立。进而提高机械故障诊断的准确性。

1　理论背景介绍

1.1支持向量机理论

支持向量机 （Support Vector Machine，SVM）是由Cortes 和Vapnik首先发现并提出的，支持向量机方法的建立是基于统计学的VC维理论和结构风险最小原理来完成的，能够结合样本信息进行学习精度以及无错误识别样本能力之间获得最佳折衷，从而获取最优的推广能力[7-8]。其基本原理是（以二维数据为例，如图1所示）：在图1中若训练数据为分布在二维平面上的点，那么依据分类标准可聚集在不同的区域。这一算法的目标在于通过训练寻找各个分类的边界，其中直线代表线性划分，曲线代表非线性划分。

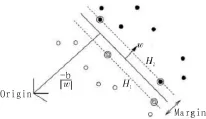
图1　线性划分示意图

支持向量机首要任务即为最简单的模式识别，即为超平面的二分类问题。先考虑两类线性可分情况。设X1，X2，…，Xn其中Xi∈Rd，i=1，…，n，n是n个d维训练样本，每个样本对应的标一记为y1，y2，…，yn，其中yi∈{1，-1}，i=1，…，n标明该向量属于两类中的哪一类[9]。若超平面wT·x＋b能将训练样本分开，则有：

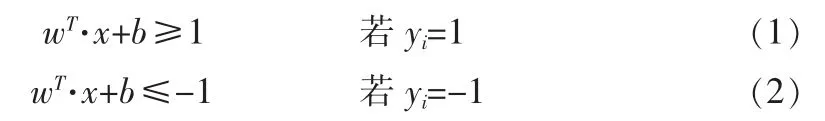
SVM的目标在于优中选优，如图1中选择最合适的分类面H1，H2分别代表能够通过各类样本中离分类线最近的点并且还能够与分类线的直线平行的分类线，H1和H2之间的距离则被称为是两类的分类空隙 （margin）。线性判别函数表示为g（x）=w·x＋b，分类面方程为:w·x＋b=0。实现所有样本正确分类，就是要求它满足

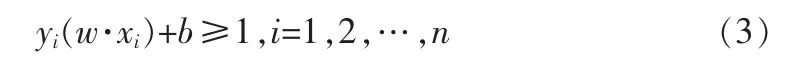
而式（3）中使等号成立所对应的样本，则被称为支持向量（Support Vectors）。因此问题转换为约束优化问题，其可采用拉格朗日方法进行求取，拉格朗日函数因此定义如下：

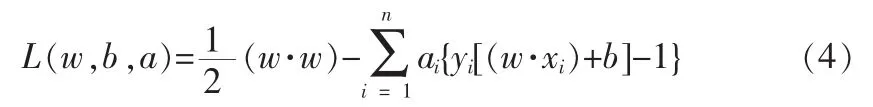
采用拉格朗日算法计算后则可获得最优分类函数是：

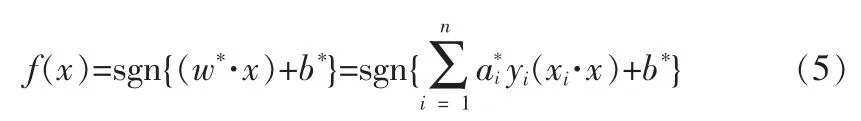
sgn（）为符号函数。如上所述，非支持向量的ai均为0，分析非线性划分问题，我们发现能够通过采用非线性变换中Φ：Rd→H实现向高维空间H中线性的转换。通常情况下，这种变换形式是较为复杂不易于实现的。然而，分析上述问题，我们发现，不管是目标函数还是分类函数的优化均只是涉及了向量的点积运算，即Φ（xi）·Φ（xj）的形式[10-11]。如果存在一个“核函数”K，满足：

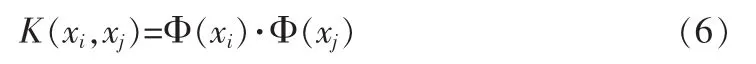
原空间中的函数则可以用来进行变换空间中的点积，进而避免映射Φ的具体形式常见的满足Mercer条件的核函数有[12]：

线性核函数：K（x，y）=x·y

多项式核函数：K（x，y）=（γx·y＋r）p，r＞0

高斯径向基函数：K（x，y）=exp（-γ‖x·y‖2），γ＞0

两层感知器核函数：K（x，y）=tanh（γx·y＋r）

1.2基于交叉验证的SVM优化算法

交叉验证（CV）是进行分类器性能验证常用的一种方法，核心思想在于将原始数据首先进行分组，其中一部分作为训练集，其余的部分作为验证集，然后再训练集对分类器进行相应的训练。并通过验证集进行训练模型的验证，从而获得准确率较高的性能指标[13-14]。其中K-交叉验证是交叉验证方法的衍生的一种模式，其计算过程为对原始数据被均分为K组，并针对分割好的K个子集一一进行验证，同时将剩余的K-1组子集作为训练集，因此，将得到K个模型，分类进行模型的验证，再取其平均值作为K-CV下分类器的性能指标。一般来说，SVM参数的优化选择未有统一的方法。目前，使用最多的即为在一定的范围内进行c和g取值，然后据此将训练集作为原始数据集再通过K-CV方法获得c和g下训练集进行分类验证的准确率，并最终将准确率最高的c和g确定为最理想的参数，然而，在实际应用中，也有可能出现多组分类准确率较高的情况，在这种情况下，则需要比较选择能够达到最高准确率的组合最小的那组。c和g做为最佳的参数，如果对应最小的有多组g，就选取搜索到的第一组c和g做为最佳的参数。究其原因，过高则有可能导致学习状态发生。因此，在所验证的最高分类准确率中，较小的惩罚参数的c和g则应该是更理想的参数。

1.3基于交叉验证方法的支持向量机模型优化建立流程

通过上述内容，本文设计基于交叉验证的基本流程如下：

1）所有特征值归一化；

2）选择较好的核函数；

3）使用K交叉验证（cross-validation）选择较好的参数（C 和gamma）；

4）用找到的参数来训练得到分类模型（model）；

5）载入分类模型对测试样本进行分类。

2　基于支持向量机的机械设备故障诊断实验

2.1机械设备故障特征数据处理

汽轮发电机是重要的机械设备，并且应用广泛，本文采用汽轮机的常见故障进行分析，汽轮发电机组典型的故障类型分别是不平衡、碰磨、松动共3类，故障数据从模拟转子实验台获得，从中选取5组已知类别的故障样本共90个进行训练。信号以频谱分析为基准，采集数据经过归一化作为输入征兆，其中部分数据如表1所示。其中频域征兆，A:≤0.5f1，B:（0.51～0.99） f1，C:1f1，D:2f1，E:（3～5）f1，F:odd f1，G:＞5f1其中，f1为转速工频。

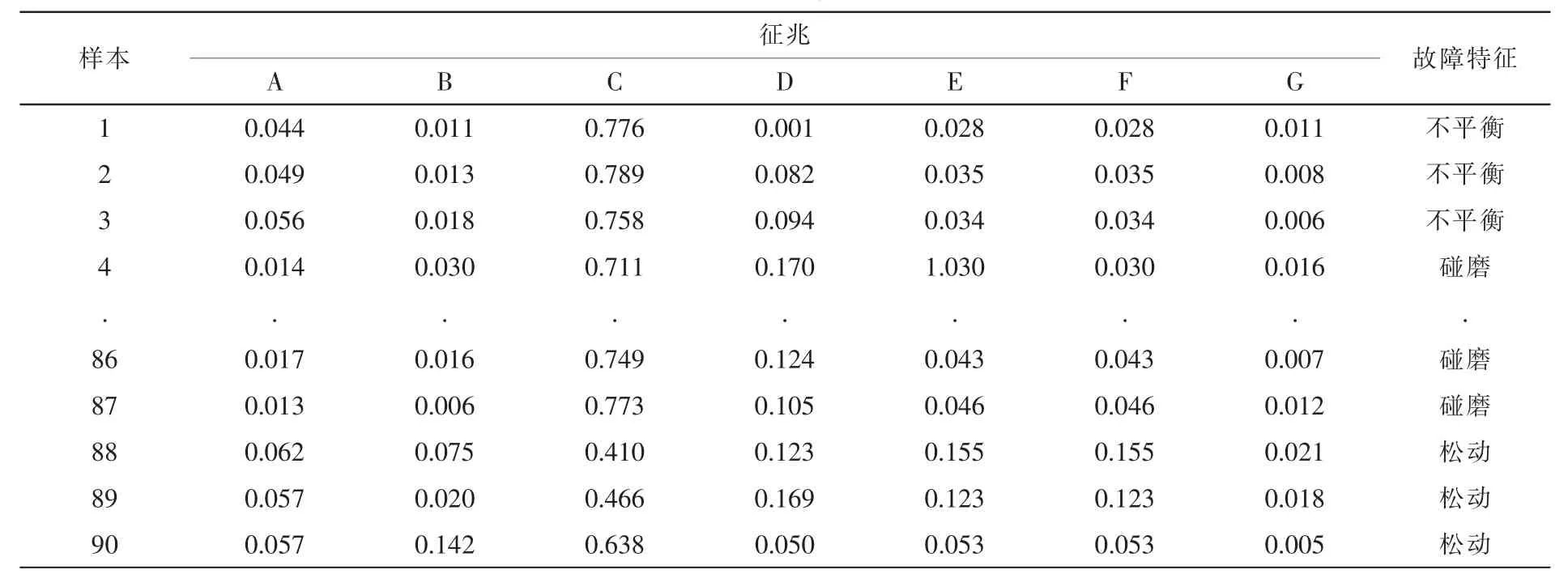
表1　汽轮机故障特征数据

2.2基于K-交叉验证的支持向量模型建立

经过了归一化处理的汽轮发电机故障数据则可进入SVM分类识别模块，首先将这90个样本进行分类，其中将故障数据的50%作为训练集，其余的作为测试集，并采用训练集进行SVM的训练获得分类模型，再通过测试集将获得的分类模型进行测试。训练过程中可分别选择4种不同的核函数进行SVM模型的建立，其中每种核函数下核参数c和特征参数g需要进行最优化计算，只有通过最优化计算后的核参数c和特征参数g构建出来的SVM模型才能实现最优的分类效果，文中采用前面介绍的K-CV方法进行核参数c和特征参数g的求取。其计算过程可以将c和g在一定范围内进行离散查找，直到查找到最优参数为止，这里将c和g在2的指数范围网格内进行查找。其中：cmin:惩罚参数c的变化范围的最小值（取以2为底的幂指数后），即c_min=2cmin，默认为-10。cmax；惩罚参数c的变化范围的最大值（取以2为底的幂指数后），即c_max=2cmax，默认值为10。gmin:惩罚参数c的变化范围的最小值（取以2为底的幂指数后），即g_min=2gmin，默认为-10。gmax；惩罚参数c的变化范围的最大值（取以2为底的幂指数后），即g_max=2gmax，默认值为10。c和g的搜索步长为1，应用LIBSVM工具箱则可进行核参数c和特征参数g交叉验证的选取[15-16]。文中对采用多项式核函数下的交叉验证选取结果，如图2所示。

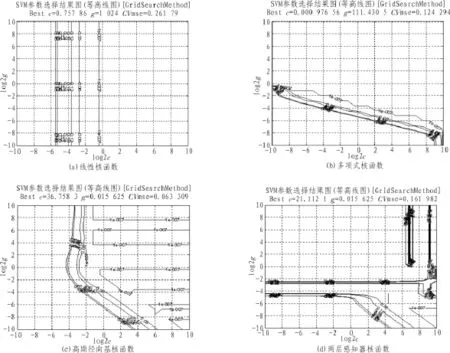
图2　不同核函数下K-CV验证结果

上述图形的含义是，横轴代表c取以2为底的对数后的值，Y轴代表g取以2为底的对数后的值，等高线代表取相应的c和g后所对应的K-CV方法的准确率，结合图能够看出c的范围为2-10到210，而g的范围为2-10到210。图2分别为4种不同核函数下进行交叉验证结果下的最优核参数c和特征参数g组合，从图中可以看出，在训练过程中采用线性核函数后进行K-CV交叉验证后当c=0.757 8，g=1 024时训练样本的误差为0.26。采用多项式核函数后进行K-CV交叉验证后当 c=0.000 97，g=111.43时训练样本的误差为0.124。采用高斯径向基核函数后进行K-CV交叉验证后当c=36.75，g=0.015时训练样本的误差为0.063。采用多项式核函数后进行K-CV交叉验证后当c=21.11，g=0.015时训练样本的误差为0.16。通过以上可以分析，对应不同核函数进行交叉验证时所获得的最优核参数c和特征参数g组合也有所不同。获取到最优参数组合后则表明已经训练完毕SVM模型，下一步则可将测试样本应用到SVM模型中进行验证该模型的可靠性。

2.3基于支持向量的机械设备故障诊断模型测试

将测试样本集带入到模型中进行模型测试，模型测试结果如表2所示。通过表2可以看出，采用不同核函数测试的结果不同，其中采用高斯径向基核函数进行测试结果的准确率最高可以达到93%，其次是采用多项式核函数的测试准确率为88%，之后是采用两层感知核函数预测的结果准确率为82%，最后的为采用线性核函数，其准确率仅为76%。同时支持向量机性能评价的另外一个指标为支持向量个数，其数量的多少直接反应了模型的建立的复杂程度和测试的时间，其中采用高斯径向基核函数进行SVM分类模型的建立只需要9个支持向量的个数，而采用多项式核函数则需要21个支持向量个数，通过测试时间也可以看出，采用9个支持向量个数的高斯径向基核函数测试过程时间只需要0.56 s，低于其他3种核函数。综上所示，通过对比可以看出，采用高斯径向基核函数和最优参数组合（c=36.75，g=0.015）进行交通标志识别的效果最好。

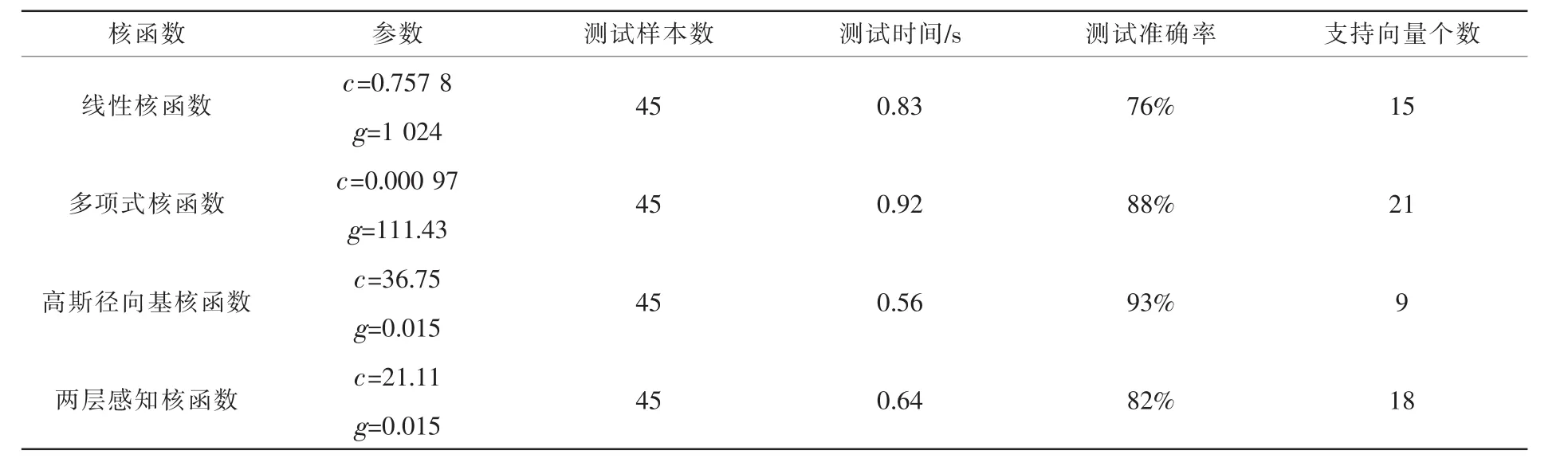
表2　SVM模型测试结果

为了对比采用SVM进行交通标志识别的优越性，文中将SVM测试结果与采用BP神经网络和KNN（K最近邻）算法和BP神经网络算法识别结果进行对比，其对比结果如表3所示。通过表3可以看出采用SVM进行汽轮发电机故障识别的准确率和测试时间都优于KNN算法和BP神经网络算法。因此采用SVM进行汽轮发电机具有最佳的效果。通过以上的实验可证明文中设计的基于SVM的汽轮发电机故障检测识别方法准确率可以达到93%，可以很好的满足机械设备的故障诊断识别。

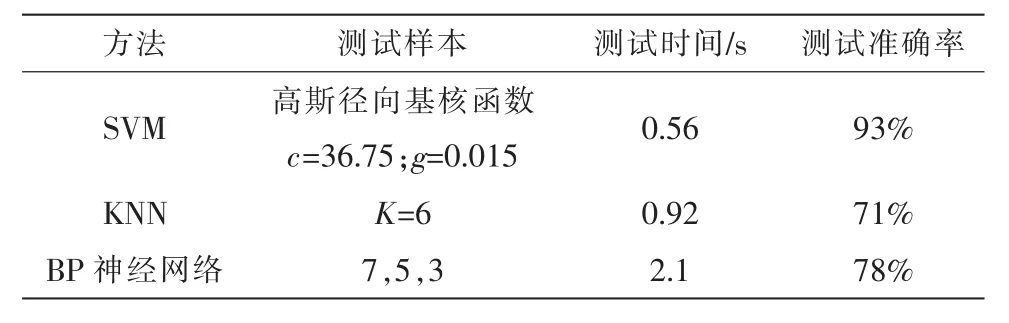
表3　3种机器学习方法识别结果

3　结　论

文中进行了基于SVM的机械设备故障诊断技术研究，其中介绍了基于统计学原理的SVM分类识别原理，并对SVM分类识别中的核参数c和特征参数g的计算采用了KCV交叉验证的方法进行最优参数计算，给出了SVM具体流程，最后进行了基于SVM的汽轮发电机故障诊断识别实验研究，实验结果表明：采用高斯径向基核函数和最优参数组合（c=36.75，g=0.015）进行汽轮发电机故障诊断识别的效果最好，同时与KNN和BP神经网络预测的结果进行了对比，最终确定了文中设计的采用SVM分类模型进行汽轮发电机故障诊断识别的效果最佳，准确度可达到93%，以很好的满足机械设备故障自动诊断识别要求。

[1]朱亚辉，黄襄念.SVM方法在模式识别应用领域中的发展与研究[J].现代计算机，2015（6）:20-24.

[2]蒋方纯，田盛丰，尹传环.机器学习置信度机制研究综述[J].北京交通大学学报，2014（3）:111-117.

[3]胡春玲.贝叶斯网络研究综述[J].合肥学院学报：自然科学版，2013（1）:33-40.

[4]占健，吴斌，王加祥.基于支持向量机的齿轮箱齿轮故障诊断[J].上海电机学院学报，2014（1）:5-10.

[5]石瑶，任清阳.基于支持向量机的矿井通风机故障诊断系统的研究[J].自动化与仪器仪表，2013（5）:18-20.

[6]牛伟，成娟，毛宁，等.基于支持向量机的转子系统早期故障诊断方法[J].测控技术，2014（9）:18-21.

[7]Cortes C，Vapnik V.Support-vector networks[J].Machine learning，1995，20（3）:273-297.

[8]林辉，王德成.支持向量机的参数优化及其在故障诊断中的应用[J].计算机科学，2010，37（4）:255-257.

[9]丁勇，秦晓明，何寒晖.支持向量机的参数优化及其文本分类中的应用[J].计算机仿真，2010，27（11）:187-190.

[10]董泽，李鹏，王学厚，等.基于粗糙集和支持向量机的汽轮机组故障诊断 [J].华北电力大学学报：自然科学版，2008 （2）:79-82.

[11]李锋，汤宝平，章国稳.基于舍一交叉验证优化最小二乘支持向量机的故障诊断模型 [J].振动与冲击，2010（9）:170-174.

[12]阎威武，朱宏栋，邵惠鹤.基于最小二乘支持向量机的软测量建模[J].系统仿真学报，2003（10）:1494-1496.

[13]江伟，罗毅，涂光瑜.基于多类支持向量机的变压器故障诊断模型[J].水电能源科学，2007（1）:52-55.

[14]郎宇宁，蔺娟如.基于支持向量机的多分类方法研究[J].中国西部科技，2010（17）:28-29.

[15]薛宁静.多类支持向量机分类器对比研究[J].计算机工程与设计，2011（5）:1792-1795.

[16]谢娟英，张兵权，汪万紫.基于双支持向量机的偏二叉树多类分类算法[J].南京大学学报：自然科学版，2011（4）:354-363.

Research on equipment fault diagnosis based on support vector machine

LIU Yi-ou
（Xi'an International University，Xi'an 710077，China）

Support vector machine as a machine learning method based on statistical theory，which plays an important role in the study of artificial intelligence.In this paper，a support vector machine intelligent recognition method is introduced to the mechanical fault diagnosis，and the penalty factor C and kernel factor g of the support vector machine model are optimized used the cross validation method.A fault diagnosis model based on the optimized support vector machine is established，and the related experiments are carried out.Experiments show that this method can effectively identify the fault types of mechanical equipment with the support vector machine method，which provides an effective diagnosis method for fault diagnosis of mechanical equipment.

support vector machine；cross validation；mechanical equipment；fault diagnosis

TN0

A

1674－6236（2016）22-0067-04

2015-11-25稿件编号：201511252

2015年陕西省教育厅科学研究项目（15JK2113）；2015年陕西省高等教育教学改革研究项目（15J37）；2016年西安市社会科学规划基金项目（16IN13）

刘一鸥（1978—），女，陕西西安人，硕士，讲师。研究方向：人工智能、软件工程。