考虑检修能力约束的动车组交路计划优化模型与算法
2016-12-05江政杰贺振欢童佳楠
江政杰, 聂 磊,贺振欢,童佳楠
(1.北京交通大学 交通运输学院,北京 100044;2.中铁二院工程集团有限责任公司 土木建筑设计 研究二院,四川 成都 610036)
考虑检修能力约束的动车组交路计划优化模型与算法
江政杰1, 聂 磊1,贺振欢1,童佳楠2
(1.北京交通大学 交通运输学院,北京 100044;2.中铁二院工程集团有限责任公司 土木建筑设计 研究二院,四川 成都 610036)
我国高速铁路动车段所数量较少且分布较为集中,动车组一级检修能力成为编制动车组交路计划的重要制约条件。鉴于此,对动车组交路计划编制问题建立考虑动车段所一级检修能力约束的多目标整数规划模型。首先,依据动车组交路接续规则和一级检修条件构造交路备选集,并将交路计划编制问题表达为集合划分问题;其次,采用基于重要性分级的分层序列法求解模型,即多目标模型被分解为主目标“动车组运用数量最小”,以及次目标“检修次数最少”的 2 个单目标整数规划模型,并采用传统的精确算法求解;最后,通过算例分析验证了模型与算法的有效性,为动车组交路计划的优化编制提供依据。
高速铁路;动车组交路;分层序列法;多目标整数规划
0引言
随着我国高速铁路的快速成网,动车组列车开行数量不断增加,动车组的运用和检修是否合理在很大程度上影响铁路部门的运营成本,动车段所的一级检修能力已经成为动车组列车开行的重要制约条件。因此,优化动车组交路计划,节省动车组运用数量,降低动车组检修成本,成为高速铁路运输组织面临的重要现实问题和技术难题。
在既有的研究中,我国大多数学者通过整数规划模型对动车组交路计划进行建模,并分别以动车组数量最少和动车组检修次数最少为优化目标;求解算法则有分枝定价算法等精确算法,以及粒子群算法、蚁群算法等智能算法。在精确算法方面,王莹等[1-2]通过研究动车组运用规程的特点,构建接续网络模型,并采用分支定价算法进行求解;LU C等[3]基于贪婪算法构造接续网络,并采用分支定界算法进行求解。在智能算法方面,李华等[4]、ZHOU Y等[5]基于给定成对列车运行图建立多目标整数规划模型,并采用改进的蚁群算法进行求解;王忠凯[6]将动车组交路计划抽象为带状态约束的旅行商问题,构建相应的接续网络,并且采用蚁群算法进行求解;李华等[7]、李建等[8]则主要基于列车运行图构造动车组交路网络,采用粒子群优化算法进行求解;苗建瑞等[9]将动车组交路计划归结为带补给的多旅行商问题,采用分层优化启发式算法进行求解;黄兴亮[10]分析影响动车组交路计划编制的因素,构建动车组交路计划编制与列车运行图协调优化的模型,并且采用改进的蚁群算法进行求解;陈然等[11]针对动车组列车网络化运行条件下的复杂情况,将编制动车组运用计划的经验加入专家系统,通过设计基于专家系统指导的最大最小蚁群算法对模型进行求解;余晓园等[12]分析高速铁路列车开行模式对动车组运用的影响,提出基于列车接续网络的动车组交路计划优化模型,并运用 Cplex 软件进行求解。
既有研究中大都以动车组数量和检修次数的线性加权最小为目标函数,但目标权重系数依赖于决策者的主观判断,在实际应用中难以客观地确定;并且对于2个定位不同的目标,加权目标实际意义不明确。因此,首先基于王昕[13]提出的思路,通过分析交路生成的可行性和合理性约束,建立动车组交路备选集,从而将问题通过多目标整数规划建模;进而,基于重要性将目标函数进行分级,并通过分层序列法对模型进行求解;最后通过算例验证模型的有效性。

图1 动车组交路计划示例
1问题描述
定义动车组交路段为单个动车组或重联动车组担当的列车或列车组合;动车组交路则由单个或若干个动车组交路段组成,在动车组列车运营过程中周期性地重复执行。动车组交路计划示例如图 1 所示。在同一个交路中,2 个相邻交路段中前一交路段的终到站必须与后续交路段的始发站一致;交路中最后 1 个交路段的终到站必须与第 1 个交路段的始发站一致。在图1中,动车组 L1 所担当交路段 1 的始发、终到站一致,因而交路段 1 构成单日交路;而交路段 2 的始发站和交路段 3 的终到站一致,并且交路段 2 和交路段 3 符合相邻的接续关系,因而交路段 2 和交路段 3 组成 1 个双日交路。动车组交路计划是根据动车组管理和检修规程规定、动车组配属情况,以及给定的列车运行图任务,制订需要完成的列车担当任务和动车组一级检修任务的动车组运用计划。
1.1动车组交路的数学描述
1.2构建动车组交路的约束条件
动车组交路计划是高速铁路/客运专线的基本运输计划之一,编制过程中的影响因素很多。为简化问题,主要考虑以下约束条件。
(1)接续条件。由同一动车组担当的相邻 2 个交路段的间隔时间必须大于动车组在车站进行接续作业需要的最小时间;由同一动车组担当的相邻 2个交路段中,前一交路段的终点必须和后一交路段的起点相同。假定 Rh1, w1和 Rh2, w2为符合接续条件的任意 2 个交路段,tmin为最小接续时间,则有

(2)一级检修条件。根据动车组检修规程,由同一动车组担当的交路段中,列车的累计走行里程不能超过规定的一级检修累计里程 (一般为4 000 km,允许上下浮动各 10%);同时,列车的累计运行时间不能超过规定的一级检修累计运行时间 48 h。以给定的 2 d 列车运行图为基础构造的动车组交路段必然满足规定的一级检修累计运行时间约束,因而只需满足一级检修累计里程约束。

2动车组交路计划优化模型
定义动车组交路备选集合为 Rf;cr为担当动车组交路 r 的动车组数量,组,r ∈ Rf;xr为 0-1 决策变量,如果动车组交路被选择,则 xr= 1,否则为 xr= 0;Q 为动车段所集合;bq, r表示交路 r 在动车段所 q 占用的一级检修能力,组,q ∈ Q;nq表示动车段所 q 的一级检修能力,组;L 为给定运行图中的所有运行线的集合;δl, r为 0-1 变量,表示交路 r 是否覆盖列车任务 l,l ∈ L,如果覆盖则 δl, r= 1,否则为 δl, r= 0;nr表示动车组交路 r 的检修次数,如果交路里程超过一级检修里程,则检修次数为 2 次,否则为 1 次。
以动车组数量最少为主要优化目标、以检修次数最少为次要优化目标构建多目标整数规划模型。
(1)以动车组数量最少为主要优化目标建立整数规划模型 (以下简称“M-1 模型”)。

式中:公式 ⑷ 为目标函数,表示以交路方案的动车组数量最少为目标;公式 ⑸ 为动车段所检修能力约束;公式 ⑹ 为列车任务覆盖约束,要求每个列车任务必须被覆盖,并且只覆盖 1 次。
(2)从 M-1 模型可以求出当前动车组交路方案下所需的最少动车组数量,以此为约束,以动车组检修次数最少为目标建立整数规划模型 (以下简称“M-2 模型”)。


式中:公式 ⑺ 表示所选择交路方案的总检修次数最少;公式 ⑻ 表示当前选择的交路方案所需的动车组数量不能超过 M-1 模型求解得到的最少动车组数量;公式 ⑼ 和 ⑽ 与模型 M-1 的约束定义一致。
3动车组交路计划优化模型求解
3.1交路备选集构造算法
交路备选集是指具有实际开行可能的、合理的动车组交路集合,它是以列车运行图为输入,以动车组一级检修里程和时间规定、动车段所检修能力为约束条件得到的备选交路集合。以 2 d 列车运行图为基础构造交路备选集,则担当任意可行交路的列车累计运行时间满足一级检修时间周期约束。交路备选集构造算法的流程如下。
(1)以单条运行线构造交路段,得到单条运行线构成的交路段集合 R1,置迭代次数 n = 1。
(2)逐层进行广度优先搜索过程,即以 n 条运行线构成的可行交路段集合 Rn构造 ( n + 1) 条运行线的可行交路段集合 Rn+1:遍历可行交路段集合 Rn,任取 Rn中的第 i 个交路段 Rn, i,再遍历集合 R1的任意交路段 R1,j,如果满足公式 ⑴ 和公式 ⑵ 的约束条件,则将交路段 R1,j拼接到交路段 Rn, i之后,构成 ( n + 1) 条运行线组成的可行交路段,并添加到集合 Rn+1。
(3)对于 ( n + 1) 条运行线构成的可行交路段集合 Rn+1,如果交路段的始发和终到站一致,则该交路段为合理交路,将该交路添加到交路备选集 Rf中。如果存在里程超过一级检修里程的交路,则进行超修程交路的修正,将该交路的检修次数增加1 次,并将该交路分解为不超修程的 2 个交路段,担当该交路段的动车组满足约束条件 ⑶ 的里程约束。
(4)每层循环结束后,将由 ( n + 1) 条运行线构成的可行交路段集合 Rn+1保存到 R 集合中,此时如果 Rn+1中仍然有交路段存在,令 n = n + 1,转到步骤(3),否则退出循环。
(5)为提高动车组运用效率,设定每个动车组的日均车公里数不少于 1 300 km,删除交路备选集 Rf中日均车公里小于 1 300 km 的交路,得出合理的交路备选集。
3.2整数规划模型求解
整数规划求解的流程如下。
(1)根据给定的交路备选集 Rf,利用模型M-1 求解出最少动车组使用数量。
(2)根据当前交路方案求出的最少动车组使用数量,利用模型 M-2 求出当前交路方案最少检修次数,如果无解,转到步骤(3);否则退出循环,得出最少检修次数。
(3)松弛公式 ⑻ 的约束上界 F1,使最少动车组数量加 1,如果当前动车组数量超过限定的最大动车组使用数量 Fmax,则当前交路方案无解,退出循环;否则转到步骤(2)。
多目标整数规划求解流程如图2所示。
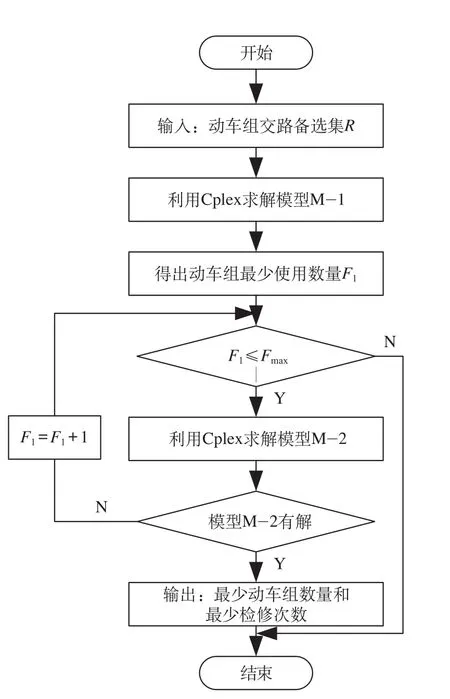
图2 多目标整数规划求解流程
4算例分析
以 2013年7月列车运行图上全部交路均在京广(北京西—广州南)、广深 (广州南—深圳北) 高速铁路上的高速和动车组列车作为研究对象,应用构建的模型和算法编制动车组交路计划,对模型进行验证。
4.1数据准备
(1)列车运行图数据。①始发、终到站包括北京西、石家庄、郑州东、济南西、西安北、信阳东、武汉、汉口、岳阳东、长沙南、广州南、深圳北站共 12 个。②各折返站的最小折返作业时间为tmin= 15 min。③开行列车 38 对/d,列车最高运行速度 300 km/h。
(2)动车组数据。①动车组一级检修里程为4 000±400 km。②动车段所检修能力。京广、广深高速铁路沿线设置的动车段所不仅承担 2 条线路上运行动车组的一级检修任务,而且还承担其他线路上的动车组检修任务。由于动车组交路的特点,每个动车段所每日实际检修的动车组数量不是定值,并且不同时段的动车段所检修能力占用情况也不同,因而应分时段考虑动车段所检修能力。实际上,由于动车组一级检修工作主要集中在 20 : 00 到次日 8 : 00 之间进行,该时段的检修能力最为紧张,因而以该时间段的动车段所一级检修能力作为检算数据。京广、广深高速铁路沿线动车段所检修能力如表1所示。

表1 京广、广深高速铁路沿线动车段所检修能力及检修数量计算结果 组
4.2计算结果
根据原运行图数据,完成算例中的全部列车运行任务实际共需要动车组 38 组,检修 36 次。依据设计的模型和算法重新编制动车组交路计划,共构造交路备选集 11 375 个,构造时间为 0.43 s;按照模型 M-1 求出最少动车组使用数量为 38 组,以此为约束条件按照模型 M-2 求解得出最少检修次数为 32 次,比原运行图规定的检修次数少 4 次,说明采用该模型能够进一步优化动车组交路计划。最后求解得到动车组交路共 31个,其中单日单条交路 24 条,两日交路 7 条,动车组日均车公里2 526 km,平均一级检修里程为 3 000 km。计算得到的各动车段所检修数量如表1所示,绘制的动车组交路如图3所示。
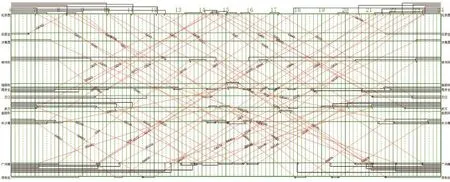
图3 动车组交路方案
5结束语
在动车组交路计划编制过程中考虑了动车段所的一级检修能力,运用多目标整数规划模型按照最少动车组数为主要优化目标,最少检修次数为次要目标,使用 Cplex 软件进行精确求解,得到满足约束条件的最少运用动车组数和最少检修次数。求解结果表明,该模型与算法可有效求解动车组交路计划编制问题,获得较优的可行解。但是,目前的动车组交路计划优化模型中考虑的约束较少,未考虑空车回送、动车组车型等条件;此外,在运行图结构固定的条件下动车组运用效率仍然存在提高空间。从优化角度出发,列车运行图与动车组交路计划应同步编制,协同优化,才能最终实现动车组运用与列车运行的最优结合。
[1] 王 莹,刘 军,苗建瑞. 基于列生成算法的动车组检修计划优化[J]. 中国铁道科学,2010,31 (2):115-120.
WANG Ying,LIU Jun,MIAO Jian-rui. Column Generation Algorithms based Optimization Method for Maintenance Scheduling of Multiple Unit[J]. China Railway Science,2010,31(2):115-120.
[2] 王 莹. 动车组运用计划和乘务计划的优化方法研究[D].北京:北京交通大学,2009.
[3] LU C, ZHOU L S, YUE Y X,et al. A Branch and Bound Algorithm for the Exact Solution of the Problem of EMU Circulation Scheduling in Railway Network[J]. Mathematical Problems in Engineering,2016 (2):1-14.
[4] 李 华,韩宝明,李得伟,等. 求解动车组交路计划的改进型蚁群算法[J]. 物流技术,2013,32(2):145-147,160.
LI Hua,HAN Bao-ming,LI De-wei,et al. Research on Improved Ant Colony Algorithm in EMU Routing Schemes[J]. Logistics Technology,2013,32(2):145-147,160.
[5] ZHOU Y,ZHOU L S,WANG Y,et al. Using Improved Ant Colony Algorithm to Investigate EMU Circulation Scheduling Problem[J]. Discrete Dynamics in Nature and Society,2014(2):1-13.
[6] 王忠凯. 动车组运用检修计划优化方法的研究[D]. 北京:中国铁道科学研究院,2012.
[7] 李 华,韩宝明,张 琦,等. 动车组交路计划优化模型与算法研究[J]. 铁道学报,2013,35(3):1-8.
LI Hua,HAN Bao-ming,ZHANG Qi,et al. Research on Optimization Model and Algorithm of EMU Circulation Plan[J]. Journal of the China Railway Society,2013, 35(3):1-8.
[8] 李 建,林柏梁,耿令乾,等. 基于交路接续的动车组运用计划优化模型与算法[J]. 交通运输系统工程与信息,2015,15(5):172-177,194.
LI Jian,LIN Bo-liang,GENG Ling-qian,et al. Optimization Model and Algorithm for Motor Trainset Utilization Scheduling based on Routes Connection[J]. Journal of Transportation Systems Engineering and Information Technology,2015,15(5):172-177,194.
[9] 苗建瑞,王 莹,杨肇夏. 基于最优接续网络的动车组交路计划优化模型与算法研究[J]. 铁道学报,2010,32(2):1-7.
MIAO Jian-rui,WANG Ying,YANG Zhao-xia. Research on the Optimization of EMU Circulation based on Optimized Connecting Network[J]. Journal of The China Railway Society,2010,32(2):1-7.
[10] 黄兴亮. 动车组交路计划编制优化理论与方法研究[D]. 成都:西南交通大学,2012.
[11] 陈 然,周磊山,乐逸祥,等. 基于专家系统的网络化动车组运用计划的编制[J]. 中国铁道科学,2016,37(1):108-116.
CHEN Ran,ZHOU Lei-shan,YUE Yi-xiang,et al. Network EMU Scheduling based on Expert System[J]. China Railway Science,2016,37(1):108-116.
[12] 余晓园,王 莹,李元凯. 高速铁路列车开行模式对动车组运用的影响研究[J]. 铁道运输与经济,2016,38(7):1-6,46.
YU Xiao-yuan,WANG Ying,LI Yuan-kai. Study on Influence of High-Speed Railway Train Operation Mode on Utilization of EMU[J]. RailwayTransport and Economy,2016,38(7):1-6,46.
[13] 王 昕. 高速铁路动车组交路与列车运行方案图协调优化方法研究[D]. 北京:北京交通大学,2015.
责任编辑:刘 新
Optimization Model and Algorithm for EMU Routing Plan with Constraint of Maintenance Capacity
JIANG Zheng-jie1, NIE Lei1, HE Zhen-huan1,TONG Jia-nan2
(1.School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China;2.The Second Civil Engineering Design & Research Institute,China Railway Eryuan Engineering Group CO.LTD, Chengdu 610036, Sichuan, China)
With less and unbalanced distribution of EMU depots in China, the capacity for Level-1 maintenance is becoming an important constraint of EMU routing plan. A multi-objective integer model for EMU routing plan is constructed with consideration of Level-1 maintenance capacity of EMU depot. Firstly, a potential set is constructed by considering the EMU route connection rule and the constraint of Level-1 maintenance condition, and the EMU routing plan is formulated as set partitioning problem. Secondly, based on the importance of the objectives, stratified sequencing method is used to decompose the multi-objective model into two single integral objective models by taking minimum number of EMU as the main objective and minimum maintenance as the secondary one, both of which can be solved by using the exact algorithm. Thirdly, a case study verifies the effectiveness of the optimization model and algorithm, and provides reference for the scheduling optimization of EMU routing plan.
High-Speed Railway; EMU Routing; Stratified Sequencing Method; Multi-Objective Integer Programming
1003-1421(2016)10-0077-06
U292.6
A
10.16668/j.cnki.issn.1003-1421.2016.10.16
2016-05-05
2016-08-29
国家自然科学基金资助项目(U1434207);中国铁路总公司科技研究开发计划课题(2013X014-C)
