考虑随机因素的编组站改编能力计算方法

谢迎春，佟 罡，冯俊杰

（1.辽宁铁道职业技术学院 铁道运输系，辽宁 锦州 121000；2.沈阳铁路局 调度所，辽宁 沈阳 110002）

考虑随机因素的编组站改编能力计算方法

谢迎春1，佟 罡2，冯俊杰1

（1.辽宁铁道职业技术学院 铁道运输系，辽宁 锦州 121000；2.沈阳铁路局 调度所，辽宁 沈阳 110002）

编组站调车作业组织是一项复杂的系统工程，调车作业组织会受到固定因素和不确定因素的影响。在阐述编组站改编能力传统计算公式的基础上，为把不确定因素准确地反映到计算过程中，使计算结果更加趋于准确，采用分析拟合法进行数据分析、样本直方图及函数拟合，并对传统计算公式进行优化处理，最后以沈阳铁路局沈阳西站下行编发场数据为基础，利用优化的方法来计算改编能力，验证了分析拟合法的有效性。

随机变量；改编能力；查标；拟合函数

0引言

编组站改编能力是铁路运输能力的重要组成部分，准确计算出编组站的改编能力，对于新建线路能力的确定、既有线扩能改造、技术站合理使用各种运输设备进行挖潜提效等具有重要意义。编组站改编能力是指在合理使用技术设备条件下，利用车站的固定设备 (驼峰和牵出线及调车场的调车线路)一昼夜内所能解体和编组各方向的货物列车数或车数。编组站改编能力包括驼峰解体能力和调车场尾部编组能力。车站设备确定之后，各项作业过程按照编组站作业计划进行，因而技术作业时间基本确定。另外一方面，由于作业人员素质和外界因素的影响，使得编组站工作也受到各种随机因素的干扰。车站技术作业时间是围绕某一确定值进行波动的随机变量，该变量既有确定性，也存在一定的随机性。

长期以来国内外的专家学者也在尝试将不确定的因素纳入到车站能力计算中来，并在车站能力的计算中取得了相应的研究成果。赵王梓等[1]提出车站技术作业占用固定设备时间数据的分析方法，通过定义参数 R 描述占用时间的随机性。方惠等[2]提出基于灰色系统理论的车站通过能力计算方法，采用序列弱化算子降低原始数据序列的波动性，根据区间估计思想与灰色系统理论计算车站通过能力方法。田亚明[3]通过设计编组站解编能力和调车线能力扩充决策变量构建编组站改编能力优化模型。唐涛[4]采用灰色理论计算车站改编能力，并以密地站为例进行验证。李映红等[5]分析现有技术站改编能力查定方法，提出了改进数据流程和数据处理系统的设计原则及功能。薛峰[6]采用灰色关联分析法，提出了改编能力关联分析模型。上述研究提供了将车站作为不确定系统的方法和思路，对研究编组站改编系统具有重要参考价值，在此基础上，运用统计学相关原理，以沈阳西站下行场为研究对象对随机因素下编组站改编能力的计算方法进行研究，重点确定采用双推单溜作业方案时的驼峰解体能力。

1传统的编组站改编能力计算方法

当编组站配备 2 台调车机车采用双推单溜作业方案时，驼峰解体能力 N解的计算公式为[7]

式中：∑t固为 2 台调车机车双推单溜时的固定作业时间；为采用双推单溜作业方案时解体 1 个车列平均占用驼峰的时间；为采用单推单溜作业方案时解体 1 个车列平均占用驼峰的时间；为驼峰调车机车应担当的取送作业中未占用或未中断使用驼峰的时间；为驼峰调车机车应担当的取送作业中占用或中断使用驼峰的时间；t客妨为 1 昼夜旅客列车横切峰前咽喉妨碍驼峰解体时间；t整备为调车机车整备作业时间；t交接，t吃饭分别为调车组人员交接班、吃饭的时间；t分解，t禁溜，t整场，t妨分别为调车作业中分解车列 (不包括解送禁溜车)、解送禁溜车、整场、交叉妨碍占用驼峰的平均时间；t间隔为驼峰间隔时间；t空程为调车机车自驼峰作业地点起动时起，经到达场入口咽喉折返与到达场车列连挂并完成试牵引时止的时间；t推为驼峰机车推送车列的时间；α空为空费系数，它反映了编组站改编设备的利用率及对改编作业的干扰状况，通常由经验值确定。目前在实践中，车站改编能力的确定主要采用传统的查标方法，即选择车流波动较小并且能反映编组站车流状况的时段，连续查标 3 昼夜，最终利用车站各项技术作业的平均时间进行定标。查标方法属于统计方法[8]，其结果必然受到样本偏差和小概率事件的影响，而且使用平均值计算改编能力不能反映随机因素的影响情况，因而提出科学合理的方法来解决样本偏差和小概率事件十分必要。

2考虑随机因素的编组站改编能力计算方法——分析拟合法

编组站是一个受固定因素和多种随机因素影响的复杂系统，在考虑随机因素影响时，需要把系统拆分为受固定因素或者单一随机因素影响的子模块。利用拟合工具对查标样本值进行处理，并通过概率分布函数来消除样本偏差，能够比较真实地反映出随机因素对改编系统的影响。

2.1数据分析

根据编组站各项作业时间受到固定因素影响程度的不同，可将其分为强约束生产时间、弱约束生产时间和随机约束生产时间 3 种情况。生产时间受到约束较强并且波动较小时，可以认为该生产时间为常量，称其为强约束生产时间；生产时间受到较弱的随机因素影响并且对改编系统影响较小时，称其为弱约束生产时间；生产时间受到较强的随机因素影响并且对改编系统影响较大时，称其为随机约束生产时间。

（1）强约束生产时间。①t交接，t整备，t吃饭根据实际情况而定，为强约束生产时间，属辅助生产时间范畴。强约束生产时间可以通过加强管理和督促得到强制执行，因而在计算改编能力时把其作为常量，其值以《车站工作细则》中的规定为准。②t取送是货场、专用线取送作业占用的总时间，为强约束生产时间，属于固定生产时间的范畴，通常取 3 昼夜取送作业时间的平均值，如果t取送波动较大则需要增加样本数量。

（2）弱约束生产时间。①t空程是单推单溜方式下调车机车单机挂车所用时间，主要由单机走行距离、平均速度、连挂作业的时间决定的，为弱约束生产时间。②t妨碍，t整场，t禁溜，t间隔这些生产时间受作业次数影响较大，并且每次作业时间也存在不确定性，为弱约束生产时间。但是，由于在计算能力时，t妨碍，t整场，t禁溜，t间隔产生的频次少，时间波动较小，采用直接计算法时还要把时间分摊到每一次的解体时间中，由于计算精度的关系，可以按照强约束生产时间处理。

（3）随机约束生产时间。t分解是指分解车列的时间，受调车钩数和车组大小影响，随机性较强，为随机约束生产时间。

2.2随机变量样本函数拟合

假设某一随机变量在查标过程中获得的样本值为集合 X = {x1，x2，…，xi，…xn}，则可通过绘制直方图的方式反映不同 xi出现的频次，并根据直方图来拟合曲线和概率密度函数。绘制直方图和函数拟合可以利用 MATLAB 或 ORIGIN 等工具完成。查标过程中调车作业会受到非正常因素的影响使样本中出现小概率事件；这些小概率事件是一些出现频次较低的特殊作业或是由偶然因素影响而产生的作业时间，可通过设置置信区间来消除小概率事件对编组站改编能力的影响。

2.3传统公式优化

（1）空费时间和空费系数的确定。空费时间指除了待业时间之外，作业中不能被利用的时间。由于作业衔接的关系，空费时间不可避免。空费时间的计算公式为

式中：t空为空费时间；t固为固定作业影响驼峰作业时间；t主为主要作业占用驼峰时间(包括间隔时间)；t待业为调车机车等待作业时间。

空费时间是一个受到作业次数和单次空费时间影响的随机变量。为了减少随机变量的影响，在能力计算中通常采用空费系数 α空进行修正。空费系数的计算公式为

由公式 ⑸ 和 ⑹ 可知，空费系数需要通过 1 d (1 440 min) 内的空费时间来确定，如果仅仅利用查标的数据确定空费系数，则会由于样本数量不足造成空费系数和实际差别较大，因而空费系数的确定需要查标之外的大量生产数据作为样本。

（2）随机约束生产时间优化。假设某一项随机约束生产时间查标样本为集合 T随机，在能力计算中该项随机约束生产时间利用 t随机来代替传统的样本平均值进行计算。

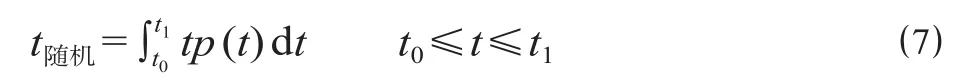
式中：p (t) 为 t随机的样本集合 T随机概率密度函数；t0，t1为概率密度置信区间。

（3）弱约束生产时间对能力影响较小，在计算中采用样本均值或按《车站行车工作细则》规定。

（4）强约束生产时间在计算中采用样本均值或《车站行车工作细则》规定。

（5）其余计算公式与传统公式相同。

3算例分析

沈阳铁路局沈阳西站为纵列式编组站，在驼峰进行解体、峰尾牵出线进行编组时，改编能力按照驼峰解体能力、尾部编组能力二者中较小者的 2 倍计算。以沈阳西站下行编发场数据为基础，利用优化的方法计算改编能力。

步骤 1：对原始数据进行分析归类。根据查标结果和《车站行车工作细则》，经过分析整理后得到以下结果。

随机约束生产时间：t分解= 9.91 min (均值)。

其他：α空= 0.05。

步骤 2：利用 ORIGIN 工具绘制随机约束生产时间 t分解的概率直方图，并拟合概率密度曲线如图1所示。利用 ORIGIN 工具输出拟合曲线的相关参数如图 2 所示。

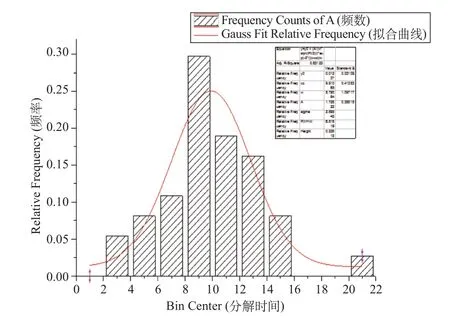
图1　t分解概率密度拟合曲线

图2　概率密度拟合函数及参数

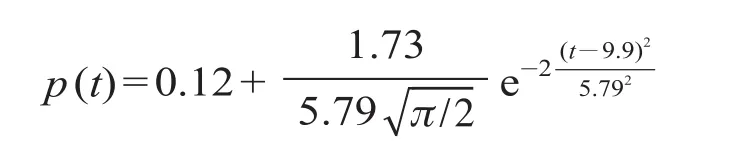
步骤 3：计算置信区间。通过图1 可以看出分解时间主要集中在 2～16 min 之间，分解时间小于2 min 的概率为 0.025，分解时间大于 18 min 的概率为 0.025，因而置信水平置信为 95% 时样本取值为{t |2≤t≤18}。

步骤 4：将拟合结果带入公式 ⑴—⑺ 进行计算。

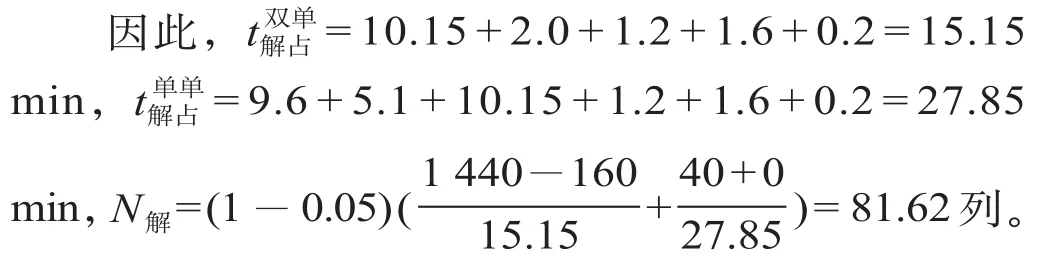
利用分析拟合法得出 t分解= 10.15 min，N解= 81.62 列。传统计算方法得出的 t分解= 9.91 min，N解= 82.93 列。通过比较可知，传统计算方法只是通过计算 t分解的样本均值而得出 N解；而分析拟合法通过拟合函数弥补了样本不足带来的误差，清晰地展现了样本的波动情况，并且对查标样本进行甄选，去掉了小概率事件的影响，采用样本加权平均值计算 N解。由于 t分解由拟合函数得出，可以通过 t分解分析出 N解的波动情况，从而较好地解释编组站改编量超过改编能力的现象。因此，通过分析拟合法计算的结果更为合理。

4结束语

在查标过程中如何处理编组站系统中随机因素的影响，准确查定编组站的真实能力，一直是一个技术难题。由于编组站改编系统涉及的随机因素较多，不同的随机因素对编组站改编系统的影响也不尽相同。因此，处理随机因素时应根据其产生作用的不同，分别进行处理，这样既简化了随机系统的复杂程度，又突出了重点的随机因素。由于在生产过程中特殊作业或者特殊因素影响会产生小概率事件，而这些小概率事件得出的生产数据并不符合实际情况，而采取分析拟合法可以计算出统计置信区间平均值，在计算过程中剔除小概率事件的影响，通过拟合曲线可以分析出随机因素的波动情况，最终确定合理的车站改编能力。对改编系统影响较弱的随机因素取值需要一个长期的生产数据采集过程，这些随机因素的确定及取值还有待进一步深入研究。

[1] 赵王梓，王慈光. 车站技术作业占用固定设备时间数据的分析[J]. 铁道运输与经济，2008，30(5)：83-85.

ZHAO Wang-zi，WANG Ci-guang. Analysis on Time Data of Fix Equipment Occupation during Station Technical Operation[J]. Railway Transport and Economy，2008，30(5)：83-85.

[2] 方 惠，王慈光，赵 亮. 基于灰色系统理论的车站通过能力计算方法研究[J]. 铁道运输与经济，2012，34(4)：28-34.

FANG Hui，WANG Ci-guang，ZHAO Liang. Research on Calculation Method of Station Passing Capacity based on Grey System Theory[J]. Railway Transport and Economy，2012，34(4)：28-34.

[3] 田亚明. 铁路网编组站改编能力配置优化模型[J]. 铁道学报，2013，35(6)：6-12.

TIAN Ya-ming. Rail Marshalling Yards Reclassification Capacity Configuration Optimization Model[J]. Journal of the China Railway Society，2013，35(6)：6-12.

[4] 唐 涛. 技术站改编能力查定及软件开发研究[D]. 成都：西南交通大学，2014.

TANG Tao. Study on Examination and Determination for Sorting Capacity of Technical Station and Software Development[D]. Chengdu：Southwest Jiaotong University，2014.

[5] 李映红，王慈光，唐优华，等. 技术站改编能力查定方法的改进[J]. 铁道运输与经济，2004，26(7)：78-80.

LI Ying-hong，WANG Ci-guang，TANG You-hua，et al. Improve on Examination &Determination Method for the Sorting Capacity of Technical Station[J]. Railway Transport and Economy，2004，26(7)：78-80.

[6] 薛 锋. 铁路编组站改编能力影响因素的灰色关联分析[J].西华大学学报(自然科学版)，2007，26(6)：89-92.

XUE Feng. Grey Relation Theory is Applied to Analyze Resorting Capacity of Marshalling Station[J]. Journal of Xihua University(Natural Science Edition)，2007，26(6)：89-92.

[7] 刘婉玲. 车站作业计划与统计[M]. 成都：西南交通大学出版社，2013.

[8] 盛 骤，谢式千，潘承毅，等. 概率论与数理统计[M]. 北京：高等教育出版社，2008.

责任编辑：吴文娟

The Computation Method about Sorting Capacity of Marshalling Station Considering Stochastic Factors

XIE Ying-chun1，TONG Gang2，FENG Jun-jie1

(1.Railway Transportation Department，Liaoning Railway Vocation and Technical College，Jinzhou 121000，Liaoning，China;2. Traffic Control Office，Shenyang Railway Administration，Shenyang 110002，Liaoning，China)

Shunting operation organization of marshalling station is a complex system engineering issue and it is affected by both fixed and uncertain factors. based on expounding the traditional calculation formula of marshalling station sorting capacity, this paper uses analysis of the fitting method for data analysis, sample histogram and function fitting and optimized the process of traditional calculation formula in order to reflect the uncertain factors into the calculation process correctly and make the calculation results tend to be more accurate. At last, the validity of the analysis fitting method is verified by using the optimization method and real data to calculate the sorting capacity of the down direction classification-departure yard of Shenyang West Railway Station.

Random Variables; Sorting Capacity; Capacity Calibration; Fitting Function

1003-1421(2016)10-0048-05

U291.4

B

10.16668/j.cnki.issn.1003-1421.2016.10.10

2016-05-27

2016-09-20

辽宁省教育厅科研项目(L2014582)