基于FRFT的指数滤波器的设计及其在地震信号处理中的应用

摘 要：研究了分数阶傅里叶变换的原理及其在地震面波压制方面的应用，分析了传统理想矩形滤波器在分数阶域对噪声压制后存在的问题。提出采用指数函数对地震面波进行压制，研究并设计了指数滤波器的函数模型，及指数陷波器的函数模型，并将该指数滤波器应用于地震信号处理中，实验证明，所设计的指数滤波器应用在分数阶傅里叶域，可有效实现对地震面波的压制，并有效的提高地震资料处理后同相轴的连续性。

关键词：分数阶傅里叶变换；滤波器；面波；同相轴

1 概述

线性调频[1]（LFM）信号广泛应用于地震、雷达、声纳等系统中，比如陆上反射地震勘探使用可控震源产生线性调频数字信号，合成孔径的雷达信号和目标回波方位的多普勒频移信号都属于LFM信号。这类信号属于典型的非平稳信号，分数阶傅里叶变换作为傅里叶变换的推广，广泛应用于非平稳信号的分析和处理，若将傅里叶变换看作从时间轴逆时针旋转？仔/2到频率轴，那么分数阶Fourier变换作为Fourier变换的广义形式，则可以旋转任意角度以展示出信号从时域逐步变化到频域的所有变化特征，为信号的时频分析提供了更大的选择空间。另外，分数阶傅里叶变换是一种线性变换，可避免多分量LFM信号而产生的交叉干扰信号项[2-7]。

正是由于分数阶Fourier变换在时频分析中的优点而逐渐受到众多科研工作者的青睐。现今，分数阶Fourier变换已经广泛应用于科学研究和工程技术的许多领域[8]，文章以地震面波的处理为背景，分析了传统滤波方法存在的问题，并提出一种新的滤波方法。

2 分数阶傅里叶变换

分数阶傅里叶变换是傅里叶变换的一种推广，从数学的角度来看，p阶分数阶傅里叶变换可以定义为时域信号x（t）的线性积分变换，对于旋转角？琢■，p为分数情形，定义[9-10]：

LFM信号有较大的时宽和频宽，单纯的在时域或频率滤波都得不到理想的结果，通过分数阶傅里叶变换，当LFM信号的调频率与旋转角度相一致时，可使LFM信号在该方向上形成冲击函数，具有最佳的时频聚集性，这时，利用在分数阶傅里叶域上的窄带滤波，就可以很好的提取LFM信号。

3 FRFT在地震信号处理中的应用

由于地震面波和有效波混杂在一起，面波的能量比有效波能量强，几乎淹没了有效波。只有选择一个合适的旋转角度，才能使面波和有效波在时频域实现分离。在处理过程中必须通过大量的试验找出的最佳变换阶数，然后在该分数阶域内设计滤波器去除面波，达到压制面波的效果。因此，使得数据处理过程变得复杂和不确定。

文中利用分数阶自相关结合分数阶傅里叶变换的方法来对地震信号进行处理，实现使地震有效波与面波干扰波的有效分离。具体方法如下：

（1）对采集的地震信号进行分数阶自相关变换，通过得到的峰值点确定有效信号调频斜率，从而确定分数阶傅里叶变换的最佳旋转阶数p。

（2）根据第一步获得的参数对原始信号进行分数阶傅里叶变换，在分数阶域设计理想窄带滤波器实现对面波的压制。

（3）进行分数阶傅里叶反变换，得到信号的时域表示。

4 理想窄带矩形滤波器的局限性分析

实验证明采用这种方法可以有效压制高强度的面波，但从处理后数据的进一步分析发现这种方法使得地震信号有效波同相轴的连续性变差，其问题来源于滤波方法的选择。

分数阶域的滤波通常采用理想滤波器对噪声进行遮隔处理，这将导致信号因截断而产生谱泄露，使得主谱线两边形成许多旁瓣，引起不同分量间的干扰，这不仅影响频率分辨率，严重时强信号的旁瓣可能湮灭弱信号的主谱线，或者将强信号谱的旁瓣误认为是另一信号的谱线，从而形成加信号，使谱分析产生交大的偏差。

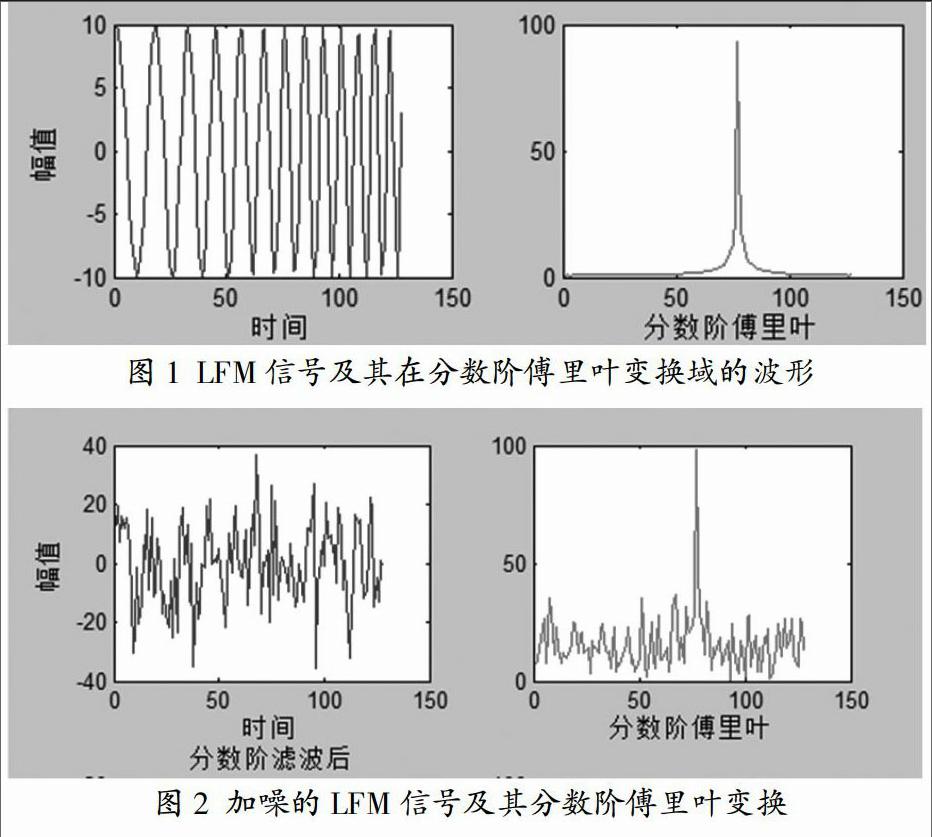
图1为理想LFM信号的时域波形及其在分数阶傅里叶变换域的波形，图2为加噪的LFM信号的时域波形及其在分数阶傅里叶变换域的波形，图3为该信号经过理想窄带滤波处理后的信号时域波形及分数阶傅里叶变换波形。通过图1和图3的对比可以发现，经过理想窄带滤波后，并没有很好的恢复原理想LFM信号的波形。原因就是某一阶次的分数阶傅里叶域的矩形波，经傅里叶逆变换回时域会使信号发生变形，形成很多旁瓣，阶次不同旁瓣的幅值也不同，这样的滤波函数与信号相乘使信号的幅值被调制而产生严重变形，从而不能很好的恢复提取信号的原来面貌。

5 压制面波的指数带陷滤波器

理想窄带矩形信号因截断效应而发生畸变使得被处理信号发生变形是不可避免的，但可通过取更长的数据作为滤波函数，使截断加宽，尽管这样会导致存储量和运算量增加。另外数据不要突然截断，也就是不要加矩形窗，而是缓慢截断，即采用幅值渐变的窗，使得窗谱的旁瓣能量更小，卷积后造成的泄露减小。

6 实验验证

以实际地震数据资料为研究对象，其中采集道数为64道，道间距为15米，采样点数为1280，采样间隔为0.004s。图7是处理前和处理后的对比结果。从滤波处理后的b图可以看到，面波得到了很好的压制，且同相轴的连续性也较好。

7 结束语

利用理想窄带滤波器在分数阶傅里叶域进行噪声压制后，再进行傅里叶逆变换回到时域时，因理想滤波器的截断效应，使得滤波处理后信号的波形发生变化。为解决这一问题，文中设计了指数形式的滤波函数，并通过试验证明该滤波函数可以有效的解决噪声压制后信号波形严重失真的问题。

参考文献

[1]Blacknell D， Freeman A， Quegan S， et al. Geometric accuracy in air borne SAR images [J]. IEEE Transations on Aerospace and Electronic Systems， 1989，25（2）：241-255.

[2]陈小龙，关键，刘宁波，等.基于FRFT的LFM信号自适应滤波算法及分析[J].现代雷达，2010，32（12）：48-59.

[3]彭建亮，彭真明，张杰，等.基于分数域自适应滤波的地震信号去噪方法[J].2012，27（4）：1730-1734.

[4]M.A.Kutay，H.Mozakats，et al.Optimal Filtering in Fractional Fourier Dominas[J].IEEE Trans Signal Processing，1997，45（5）：1129-1143

[5]M. Fatih Erden， M. Alper Kutay， and Haldun M. Ozaktas Repeated Filtering in Consecutive Fractional Fourier Domains and Its Application to Signal Restoration[J].IEEE Trans.Signal Processing，1999，47（5）：1458-1462.

[6]R.Sarikara，Yuqing，G.Saon. Fractional Fourier Transform Features for Speech Recognition[J].Processing of ICASSP04，vol.1.NJ，USA：IEEE，2004，529-532.

[7]P.Lainsleigh，N.Kehtarnavaz.Characterization of Transient Wandering

Tones by Dynamic Modeling of Fractional Fourier transform[J].Processingof ICASSP00，vol.2.NJ，USA：IEEE，2000，665-668.

[8]邵高平，安建平.基于FFT和FRFT的非平稳干扰估计和抑制[J].数据采集与处理，2010，25（2）：160-164.

[9]吴燕军，王华力，孙磊，等.基于FRFT的LFM信号检测与参数估计[J].军事通信技术，2012，33（4）：53-72.

[10]刘小河，王建英，杨美英.基于分数阶傅里叶变换的宽带LFM相干信号的DOA估计[J].数据采集与处理，2008，23（5）：547-550.

作者简介：雷立群（1977-），女，吉林省长春市人，单位：吉林农业科技学院机械工程学院，学历：硕士，研究方向：仪器科学与技术。