国际油气价格与汇率动态相依关系研究:基于一种新的时变最优Copula模型
2016-12-03刘炳越
姬 强,刘炳越,2,范 英
(1.中国科学院科技政策与管理科学研究所能源与环境政策研究中心,北京 100190;2.中国科学技术大学统计与金融系,安徽合肥 230026;3.北京航空航天大学经济管理学院,北京 100190)
国际油气价格与汇率动态相依关系研究:基于一种新的时变最优Copula模型
姬 强1,刘炳越1,2,范 英3
(1.中国科学院科技政策与管理科学研究所能源与环境政策研究中心,北京 100190;2.中国科学技术大学统计与金融系,安徽合肥 230026;3.北京航空航天大学经济管理学院,北京 100190)
本文提出一个新的时变最优Copula模型,可以准确识别二元时间序列任意时点最优的相依结构。该模型构造了半旋转copula以刻画非对称的反向相依关系,并引入独立性的无分布检验证实相依关系的存在性。同时,我们对能源商品市场(原油、天然气)、外汇市场间动态相依关系进行了实证分析,实证结果表明跨市场相依结构类型确实是时变的,突发事件往往是相依结构突变的主因。另外,时变最优Copula模型的主要优势在于不仅能够捕捉相依方向和相依强度的动态性,还能有效捕捉相依结构类型的动态性。
尾部相依;跨市场协同运动;时变最优Copula模型
1 引言
2008年金融危机爆发后,国际资本市场风险加大,市场间传染效应凸显,如何刻画跨市场动态相依关系,特别是极端事件下的相依结构成为构建资产投资组合和市场风险管理的重要内容。Copula模型由于可以捕捉非线性的相依关系以及尾部相依性(极端风险相依),成为度量市场协同运动的有力工具,在市场相依结构分析中得到了广泛的应用[1-5]。
关于copula方法的早期研究主要采用静态、单一copula方法,研究问题集中在股票、外汇、债券等金融领域以及风险管理领域[6-13]。而对copula方法的改进主要从两个方面展开:①构造多个copula的凸组合形成混合copula模型[14-15];②对单一copula相依参数构建时变方程[15-18]。由于以往的研究主要集中在金融市场内部,得到的结论通常是市场存在非对称的正向协同运动关系,这种非对称的正相依结构由已有的copula方法进行刻画非常合适。但是,跨市场间相依关系往往会呈现反向关系,比如美元汇率贬值往往会伴随以美元定价的大宗商品价格的上涨[19-21]。然而,大部分常用的非对称copula函数无法刻画此类反向协同运动关系,而对称的正态copula或t copula虽然能够刻画反向协同运动,但限定市场间相依结构具有对称性,很难刻画极端风险下的非对称现象。同时,采用只能度量同涨(跌)的上(下)尾相依函数进行分析,往往会忽略跨市场中可能存在的反向极值相依,从而得出不存在极端协同运动的结论,与实际情况不符。因此,本文主要解决如何确定跨市场动态相依结构以及尾相依度量等问题,特别是对市场间反向不对称相依关系进行有效刻画。
本文提出一种新的时变最优Copula模型,能够有效度量在市场极端风险下的跨市场动态相依关系。主要贡献如下:①构造半旋转Gumbel copula函数,对市场间非线性、非对称的反向协同运动进行刻画。②引入独立性的无分布检验,提出了数据驱动的时变最优Copula识别方法,准确识别每个时间点上的最优匹配的copula模型。③以能源市场(原油、天然气)、外汇市场(美元)为例,采用时变最优Copula模型分析跨市场间的正向和反向动态相依结构。
下文主要分为以下几部分:第二节,我们构建了时变最优Copula模型的理论框架;第三节,我们以能源市场、外汇市场为例进行实证分析;最后是结论。
2 模型方法
由于受到市场基本面、突发事件和外部信息流入等多维因素的交互影响,市场间相依结构是随时间动态变化的,其较高的复杂性意味着采用单一、静态的copula函数很难准确并完整地刻画这一动态特性。因此,本节首先根据Patton[22]的想法,构造了半旋转Gumbel函数,弥补了Gumbel copula(或旋转Gumbel)只能刻画正向相依结构以及上尾(或下尾)相依的不足。其次,在此基础上,提出数据驱动的时变最优Copula识别方法,对不同市场间的时变相依结构进行准确刻画。
2.1 copula函数建模
Copula是一个多元分布函数,其边缘分布是[0, 1]区间的均匀分布。二元copula的严格定义为:若随机变量U,V~Uniform(0, 1),则二维随机向量(U,V)的联合分布为一个copula函数,记为(U,V)~C。根据Sklar[23],二元随机向量(X,Y)的联合分布函数F可表示为:
F(x,y) = C(FX(x),FY(y))
(1)
其中FX和FY为(X, Y)的边缘分布,C是描述(X, Y)间相依结构的copula函数。若所有的累积分布函数可微,则(X,Y)的联合密度f可表示为:
f(x,y)=c(u,v)·fX(x)·fY(y)
(2)
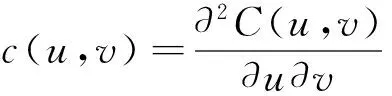
我们采用Kendall’sτ秩相关系数来刻画市场相依关系的强度和方向。同时,根据Joe[24],我们采用copula捕捉下尾和上尾相依函数以度量市场正向极端协同运动,即随机变量X、Y,其累积分布函数分别为FX、FY,对应的copula函数为C(u,v),则对于较小的α(比如0.05)。
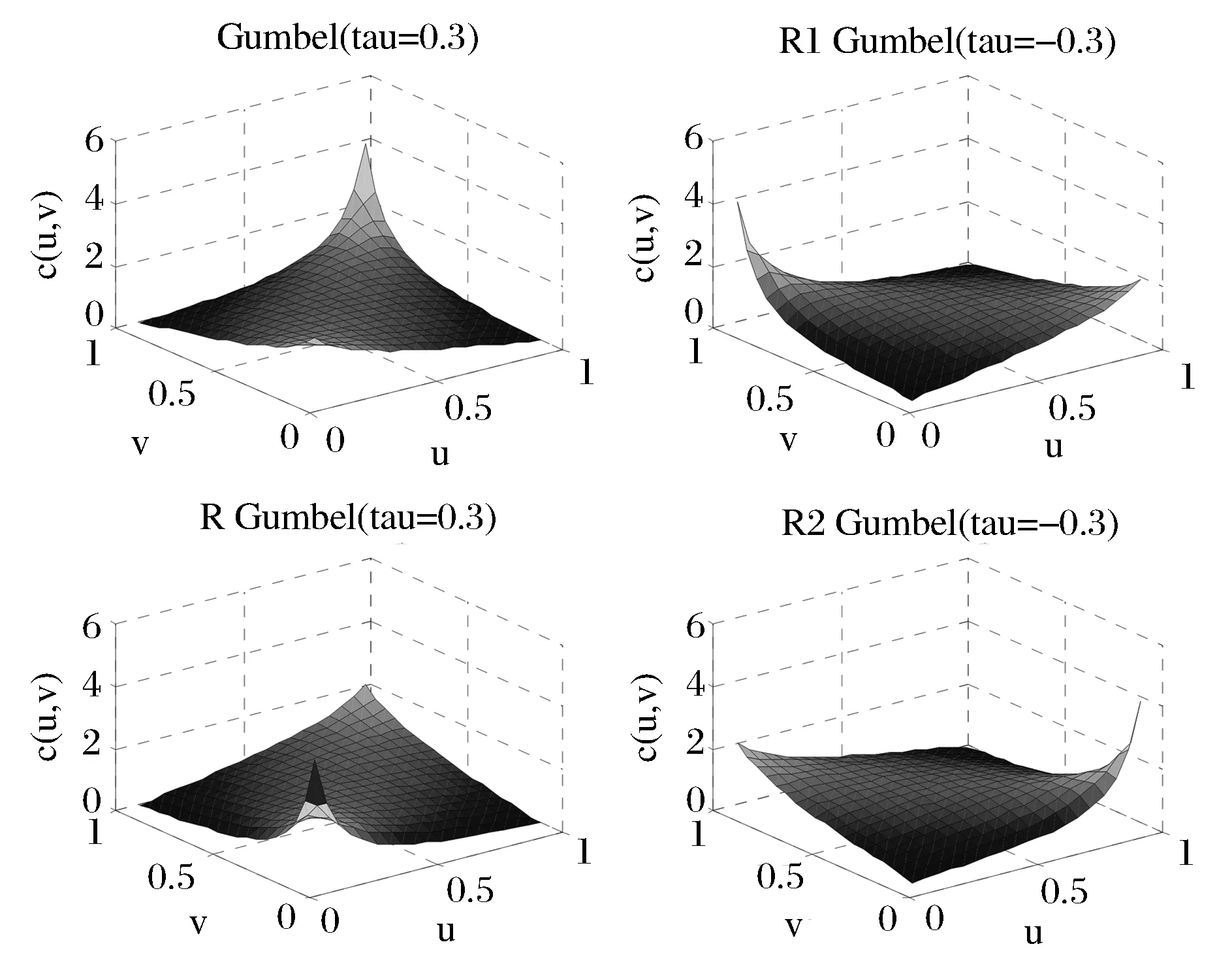
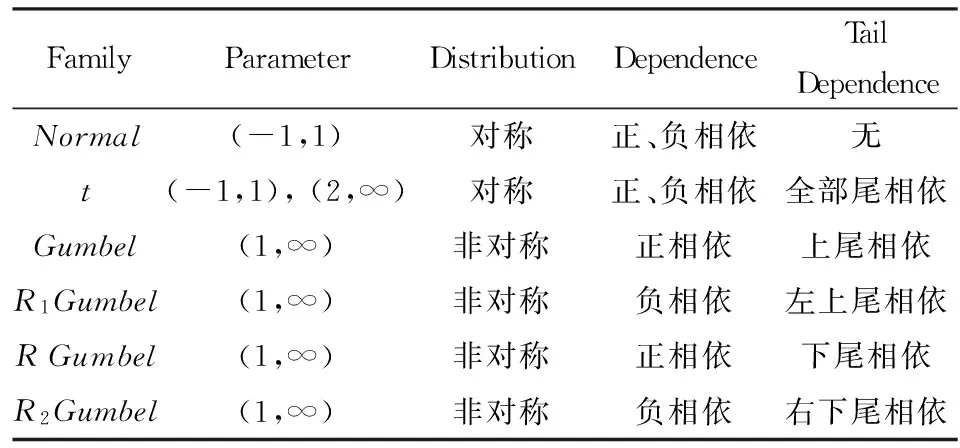
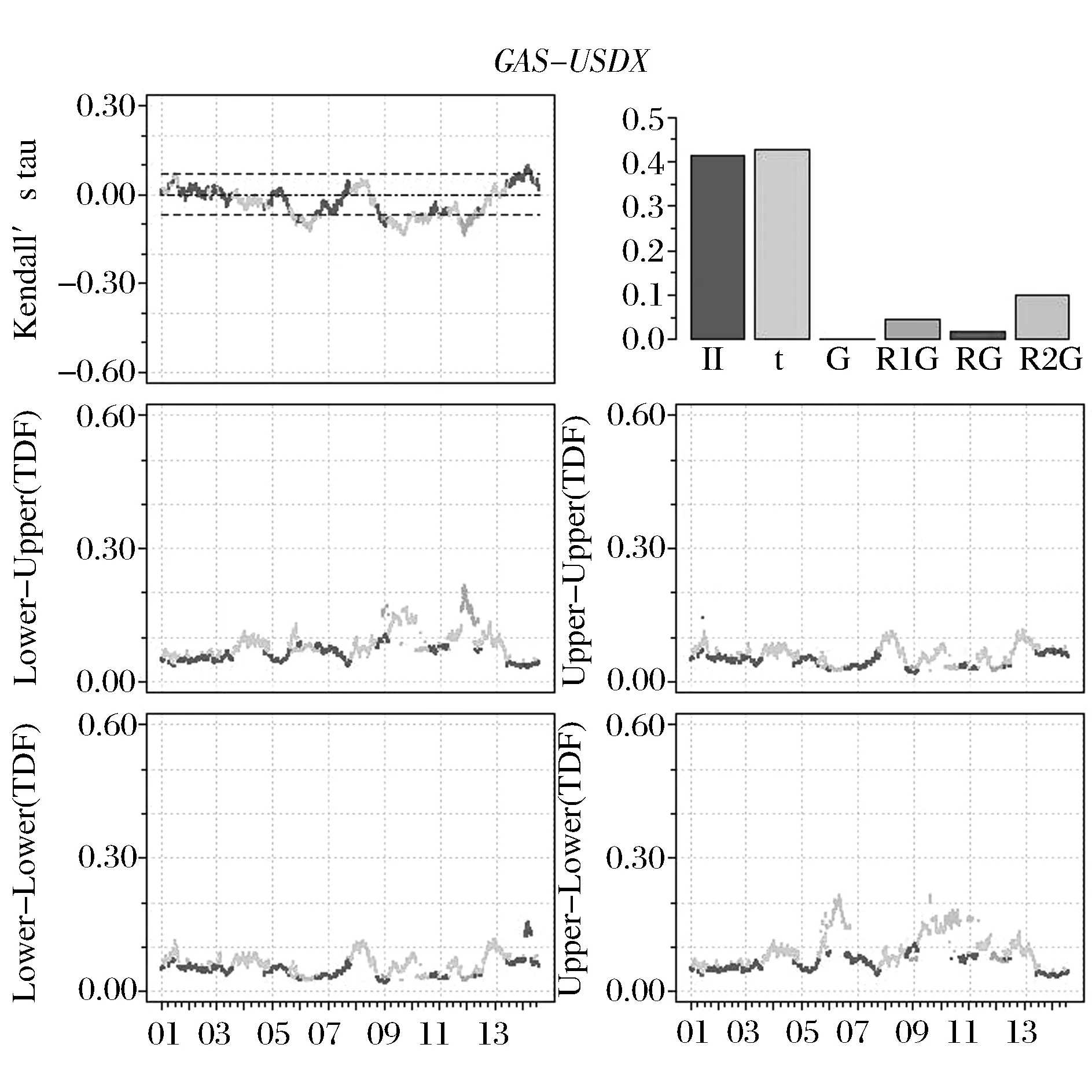
τLL(α) =Pr(X (3) (4) 另外,参照下尾和上尾相依形式,我们提出左上尾和右下尾相依函数以度量市场反向极端协同运动如下: τLU(α) = Pr(X (5) τUL(α) = Pr(X>FX-1(1-α) | Y (6) 其中,τLL(α)、τUU(α)、τLU(α)和τUL(α)分别表示下尾相依、上尾相依、左上尾相依以及右下尾相依。显然,下尾相依τLL(α) 和上尾相依τUU(α)仅能刻画市场间同向极端协同运动,而左上尾相依τLU(α)和右下尾相依τUL(α)则能度量市场间反向极端协同运动。为了捕捉跨市场间非对称的左上尾相依τLU(α)和右下尾相依τUL(α),本文对Gumbel copula函数进行了扩展(具体见2.1.1节)。 2.1.1 Copula半旋转变换及其相依性质 一般地,常用的copula函数有Normal、t、Gumbel等。其中,Normal copula和t copula均可以描述对称的正、负相依性,但Normal copula不具有尾部相依,而t copula具有对称的尾部相依。Gumbel copula可以描述非对称的正相依性,且具有上尾相依,而旋转Gumbel(生存Gumbel)能够捕捉下尾相依。为捕捉非对称的左上尾τLU(α)和右下尾相依τUL(α)等极端相依,我们构造了半旋转Gumbel copula函数如下。 可以证明,当U~Uniform(0,1)时,1-U~ Uniform(0,1)。为捕捉各种类型的跨市场相依关系,我们给出定理1~定理3的严格证明。其中,定理1给出了半旋转Gumbel copula分布的具体形式,定理2探讨了Gumbel类copula与Kendall’sτ秩相关系数的关系,定理3给出了左上尾、右下尾相依与copula函数之间的关系。 定理1:对于Gumbel copula分布COG(θ),如果二元随机向量(U, V)满足U, V~Uniform(0,1)且(U, V)~COG(θ),令ciG(u,v;θ)为copula CiG(u,v;θ)的密度函数(i∈{O,R1,R2}),则: (1-U,V)~CR1G(θ),CR1G(u,v;θ)=v-COG(1-u,v;θ), cR1G(u,v;θ) = cOG(1-u,v;θ), θ∈ΘG (7) (U,1-V)~CR2G(θ), CR2G(u,v;θ) = u-COG(u,1-v;θ), cR2G(u,v;θ) = cOG(u,1-v;θ), θ∈ΘG (8) 证明:记(U, V)~COG(θ),则COG(u,v;θ) = Pr(U≤u,V≤v)。令U′=1-U,V′=V,由copula定义,有(U′, V′)~CR1G(θ),则: CR1G(u,v;θ)=Pr(U′≤u,V′≤v)= Pr(1-U≤u,V≤v)=Pr(V≤v) -Pr(U<1-u,V≤v)=v-COG(1-u,v;θ) 同理, CR2G(u,v;θ) = u-COG(u,1-v;θ) cR1G(u,v;θ) = cOG(1-u,v;θ), θ∈ΘG cR2G(u,v;θ) = cOG(u,1-v;θ), θ∈ΘG. # 定理2:Copula CiG(θ)(i∈{O,R})只能拟合具有正相依关系的随机向量,而Copula CiG(θ) (i∈{R1,R2})只能拟合具有负相依关系的随机向量。 证明:根据引理1, 同理, 定理3:对于任一Cij, i∈{O,R1,R,R2}, j∈{N,t,G}(当i=O时, j∈{N,t,G};当i∈{R1,R,R2}时, j=G),对于较小的α(比如0.05),其尾相依函数可表示为: (9) (10) 证明:由copula,可以得到相应的随机变量X和Y均不超过给定的分位数的概率,即: C(u,v)=Pr(X≤FX-1(u),Y≤FY-1(v)), 因此,对任意给定的Cij(u,v;θ),i∈{O,R1,R,R2},j∈{N,t,G},其左上尾相依函数为: 同理, 2.1.2 Copula性质总结 本节通过copula密度函数图(图1~2)对各种copula函数的适用范围给出更直观的描述,并总结各copula函数的性质(详见表1)。Normal、t、R1Gumbel、R2Gumbel copula函数可以刻画跨市场反向协同运动;而Normal、t、Gumbel、R Gumbel copula可以刻画市场正向协同运动。其中,Normal copula没有尾相依性,t copula有对称的尾相依性,R1Gumbel、R2Gumbel、Gumbel和R Gumbel分别具有非对称的左上尾、右下尾、上尾和下尾相依。总之,我们的copula集合可以捕捉各种类型的跨市场相依结构。 图1 Normal和t copula密度函数 图2 Gumbel-类copula密度函数 FamilyParameterDistributionDependenceTailDependenceNormal(-1,1)对称正、负相依无t(-1,1),(2,∞)对称正、负相依全部尾相依Gumbel(1,∞)非对称正相依上尾相依R1Gumbel(1,∞)非对称负相依左上尾相依RGumbel(1,∞)非对称正相依下尾相依R2Gumbel(1,∞)非对称负相依右下尾相依 2.1.3 Copula参数估计及其拟合优度检验 (11) (12) 对于copula建模而言,除了参数估计外,另外一个重要的问题是检验真实的未知copula是否为已选的copula类型,从而有如下检验, T1: H0:C∈C={Cθ:θ∈Q} vs. H1: C∉C 其中Q为R上的开子集。如果真实的未知copula属于C,则存在唯一的θ∈Q,使得C∈C。进行T1检验需要基于如下函数, (13) 2.2 时变最优Copula建模 常用的时变copula模型大多是对单一copula的相依参数建模[15-18]。这些时变copula模型均为固定copula函数类型不变,而仅仅允许copula相依参数随时间动态变化。允许copula相依结构类型变化的研究中,Guégan和Zhang Jing[28]采用二元分割程序检测copula相依类型的变化,另外机制转移copula模型可以通过引入状态变量,描述不同机制下的相依结构类型[29-30]。本文提出数据驱动的时变最优Copula识别方法,其建模过程分为最优copula建模和时变建模两步。时变最优Copula建模过程如下。 2.2.1 最优copula建模过程 在最优copula建模过程中,要明确两点:第一,样本序列正、负相依关系的显著性。第二,对应于正、负相依关系的可选copula集。因此,首先需要根据样本对(X, Y)的相依关系进行统计推断。对于序列长度为n的随机向量(X, Y),我们建立如下两个检验: T2: H0: τ=0 vs. H1: τ<0 (14) T3: H0: τ=0 vs. H1: τ>0 (15) 因此,最优copula的求解算法如下: 步骤1:采用GARCH(1,1)模型拟合t时刻子样本(时间t为子样本最后一个点),进而得到[0,1]区间的均匀分布序列。 步骤5: 从{N,t}中选择t时刻最优的copula。 2.2.2 时变建模过程 滚动窗口分析是时间序列分析的常用方法,大量文献采用滚动窗口方法对经济现象或市场特征进行动态分析[32-35]。同样,我们采用滚动窗口分析完成时变最优Copula模型的时变建模过程。参考Fan Jianqing和Gu Juan[33]和Aloui等[35],将窗口长度固定为250天,近似一年的交易期。从实证结果来看,将窗宽选取为250天的简化处理并不妨碍我们得出一般化结论。另外,对于各时间窗口内最优拟合的copula是否能够准确刻画二元序列间相依关系,我们进行了拟合优度检验。 本节我们采用时变最优Copula模型对国际原油市场、天然气市场与美元汇率市场协同运动进行实证分析。采用copula模型进行能源市场与外汇市场间相依关系的研究还十分有限[36-38]。本文中,能源市场选取Brent原油价格(OIL)和Henry Hub天然气价格(GAS),数据来源于美国能源信息署;外汇市场选取美元指数(USDX),数据来源于美国联邦储备银行。样本期从2000年1月4日至2014年8月22日。 3.1 数据与描述性统计 表2展示了石油、天然气以及美元指数日收益序列的描述性统计。在整个样本期,这些序列均为偏态(非对称)分布,且具有明显的波动聚集现象,JB统计量均显著地拒绝了序列分布的正态性假设。各收益序列以及收益平方序列的Ljung-Box统计量表明各收益序列存在显著的条件异方差,LM检验统计量也表明各收益序列存在明显的ARCH效应。以上检验结果表明,我们对各收益序列构建GARCH(1,1)模型是合理的。 3.2 跨市场协同运动 整体来看,美元与原油呈强反向协动关系,美元与天然气呈弱反向协动关系,而原油与天然气市场呈正向协动关系(见图3~5)。2008年爆发的金融危机以及2011年的欧债危机,使得OIL-USDX、GAS-USDX、OIL-GAS市场收益间的阶段性协同运动显著增强,表现为Kendall’sτ秩相关系数的值在危机爆发期明显增大,并且伴随危机影响的消除逐渐减弱。在08年~12年的整个经济危机的大背景下,OIL-USDX、GAS-USDX市场协动关系呈“W”型,OIL-GAS则呈“M”型。这也反映了不同市场间信息传染效应的强弱与外生冲击的强度有直接关系。另外,与原油市场相比,天然气市场的全球化程度不高,且其影响机制和影响因素都相对复杂,因而GAS-USDX市场间的反向关系整体很微弱。 表2 各市场收益序列的描述性统计及ARCH效应检验 注:*, **分别表示在5%和1%的水平下显著。Q,Q2分别表示收益序列、收益平方序列的Ljung-Box检验统计量。ARCH表示ARCH效应的Lagrange Multiplier检验统计量。 在整个样本区间内,Normal和t copula所占比例较大,说明在大部分时间里市场间具有对称的相依结构。而在某些特殊时期,OIL-USDX和GAS-USDX市场对中最优的copula为R1Gumbel或R2Gumbel,表明能源市场与外汇市场间确实存在非对称的反向极端相依。比如,在短暂的2008年上半年的金融危机前夕,原油市场与美元市场间最优的相依结构为R2Gumbel,Brent原油市场收益倾向大幅上涨而美元市场倾向大幅下跌;而在2011年年中的欧债危机阶段,原油市场与美元市场间最优的相依结构为R1Gumbel,Brent原油市场收益处于下行风险而美元市场处于上行通道。上述实证结果与现实情况的吻合不仅表明左上尾和右下尾相依的存在性,同时验证了采用时变最优Copula模型研究跨市场极端相依的有效性。 综上,时变最优Copula实证结果表明,跨市场相依关系强度具有明显的动态特征;相依方向也不总是表现为正或负相依,有时会出现正、负相依模式的交替;整个样本期最优的copula相依结构也随时间动态变化。因而,本文提出的时变最优Copula模型能够很好地刻画市场间相依结构模式转变的动态性,准确捕捉市场间的动态相依关系。 图3 Brent原油与美元指数动态相依图 图4 Henry Hub天然气与美元指数动态相依图 图5 Brent原油与Henry Hub天然气动态相依图 3.3 TVOC模型的拟合优度检验 为检验TVOC是否在任意时点能够准确刻画市场间相依结构,我们采用2.1.3节中的拟合优度检验对每个窗口期最优的copula进行检验,其动态检验p值如图6所示。我们能够看出在绝大多数时间点最优copula的拟合优度检验p值均大于0.05,表明TVOC模型基本可以准确刻画跨市场动态相依特征。 图6 TVOC模型动态拟合优度检验P值 本文提出了一个新的研究市场动态相依结构的方法—时变最优Copula模型,该方法适用于跨市场动态相依性分析。 研究表明时变最优Copula模型能很好地描述极端风险下跨市场相依的动态特征,主要优势在于:1)构造的半旋转Gumbel模型能够有效地刻画跨市场非对称的反向相依关系,弥补了常用的copula函数(Normal、t、Gumbel)在这方面的缺陷。2)构造的时变最优Copula模型提供了一个动态copula函数集合,能够动态捕捉各种类型的跨市场相依模式,弥补了采用单一、静态copula函数在这方面的缺陷。3)时变最优Copula模型的动态性不仅包括了相依方向、相依强度的动态性,而且还包括相依结构类型的动态性。 实证结果表明,在不同条件下,市场间相依关系的特征及程度都是不同的。在经济平稳运行期,市场间大多具有对称的相依性,最优的copula通常为Normal和t copula。在此经济背景下,相依关系的方向、程度与资产属性及其内部经济关联有关。然而,上述因素导致的跨市场相依关系往往是弱相依的。相反,在极端事件情景下,市场相依常常是非对称的,这一时期的市场间相依关系主要由极端的外部冲击决定,因而市场收益间相依关系往往呈现明显增强的趋势,市场间风险溢出效应明显加大。 因此,本文提出的时变最优Copula模型能够刻画不同机理影响下的市场间相依关系,这对于市场投资者和风险管理者灵活调整投资组合策略,规避投资风险以及防范市场风险溢出乃至金融传染等方面具有重要的意义。而且,本文构造的半旋转copula在度量非线性非对称负相依关系方面具有较大的优势,能够为市场风险管理者构建投资组合进行风险对冲提供新的分析工具。 [1] Cherubini U, Luciano E, Vecchiato W. Copula methods in finance[M]. New Jersey:John Wiley & Sons, 2004. [2] 韦艳华, 张世英. 金融市场的相关性分析——Copula-GARCH模型及其应用 [J]. 系统工程, 2004, 22(4): 7-12. [3] Penzer J, Schmid F,Schmidt R.Measuring large comovements in financial markets [J]. Quantitative Finance, 2012, 12(7): 1037-1049. [4] Wu C C, Lin Z Y. An economic evaluation of stock-bond return comovements with copula-based GARCH models [J]. Quantitative Finance, 2014, 14(7): 1283-1296. [5] 亢娅丽, 朱磊, 范英. 基于Copula函数的EU ETS和电力市场间相关性分析 [J]. 中国管理科学, 2014, 22(S1): 814-821. [6] 吴振翔, 陈敏, 叶五一, 等. 基于Copula-GARCH的投资组合风险分析 [J]. 系统工程理论与实践, 2006, 26(3): 45-52. [7] Kole E, Koedijk K, Verbeek M. Selecting copulas for risk management [J]. Journal of Banking & Finance, 2007, 31(8): 2405-2423. [8] 韦艳华, 张世英. 多元Copula-GARCH模型及其在金融风险分析上的应用 [J]. 数理统计与管理, 2007, 26(3): 432-439. [9] 叶五一,缪柏其. 基于Copula变点检测的美国次级债金融危机传染分析 [J]. 中国管理科学, 2009, 17(3): 1-7. [10] Ning C. Dependence structure between the equity market and the foreign exchange market-a copula approach [J]. Journal of International Money and Finance, 2010, 29: 743-759. [11] 李建平, 丰吉闯, 宋浩, 等. 风险相关性下的信用风险、市场风险和操作风险集成度量 [J]. 中国管理科学, 2010, 18(1): 18-25. [12] 吴吉林. 基于机制转换Copula模型的股市量价尾部关系研究 [J]. 中国管理科学, 2012, 20(5): 16-23. [13] 叶五一, 李磊, 缪柏其. 高频连涨连跌收益率的相依结构以及CVaR分析 [J]. 中国管理科学, 2013, 21(1): 8-15. [14] Hu Ling. Dependence patterns across financial markets: a mixed copula approach [J]. Applied Financial Economics, 2006, 16(10): 717-729. [15] Patton AJ. Modelling asymmetric exchange rate dependence [J]. International Economic Review, 2006, 47(2): 527-556. [16] Creal D, Koopman S J, Lucas A. A general framework for observation driven time-varying parameter models[R]. Tinbergen Institute Discussion Paper, 2008. [17] Giacomini E, Härdle W, Spokoiny V. Inhomogeneous dependence modeling with time-varying copulae [J]. Journal of Business & Economic Statistics, 2009, 27(2): 224-234. [18] Hafner C M, Reznikova O. Efficient estimation of a semiparametric dynamic copula model [J]. Computational Statistics & Data Analysis, 2010, 54(11): 2609-2627. [19] Narayan P K, Narayan S, Prasad A. Understanding the oil price-exchange rate nexus for the Fiji islands [J]. Energy Economics, 2008, 30(5): 2686-2696. [20] Ji Qiang. System analysis approach for the identification of factors driving crude oil prices [J]. Computers & Industrial Engineering, 2012, 63(3): 615-625. [21] Ji Qiang, Fan Ying. How does oil price volatility affect non-energy commodity markets? [J].Applied Energy, 2012, 89(1): 273-280. [22] Patton A J. A review of copula models for economic time series [J]. Journal of Multivariate Analysis, 2012, 110(5): 4-18. [23] Sklar A. Fonctions de répartition à n dimensions et leurs marges [J]. Publications de l’Institut Statistique de l’Université Paris, 1959, 8: 229-231. [24] Joe H. Multivariate models and dependence concepts[M]. London: Chapman & Hall, 1997. [25] Nelsen R B. An introduction to copulas[M]. New York: Springer, 1999. [26] Fermanian J D, Scaillet O. Some statistical pitfalls in copula modeling for financial applications[R]. FAME Working Paper, 2004. [27] Kojadinovic I, Yan Jun, Holmes M. Fast large-sample goodness-of-fit tests for copulas [J]. Statistica Sinica, 2011,21(2): 841-871. [28] Guégan D, Zhang Jing. Change analysis of a dynamic copula for measuring dependence in multivariate financial data [J]. Quantitative Finance, 2010, 10(4): 421-430. [29] Okimoto T. New evidence of asymmetric dependence structures in international equity markets [J]. Journal of Financial and Quantitative Analysis, 2008, 43(3): 781-815. [30] Garcia R, Tsafack G. Dependence structure and extreme comovements in international equity and bond markets [J]. Journal of Banking & Finance, 2011, 35(8): 1954-1970. [31] Hollander M, Wolfe D A. Nonparametric statistical methods[M]. New York: John Wiley & Sons, 1973. [32] Swanson N R. Money and output viewed through a rolling window [J]. Journal of Monetary Economics, 1998, 41(3): 455-474. [33] Fan Jianqing, Gu Juan. Semiparametric estimation of Value at Risk [J]. The Econometrics Journal, 2003, 6(2): 261-290. [34] Hill J B. Efficient tests of long-run causation in trivariate VAR processes with a rolling window study of the money-income relationship [J]. Journal of Applied Econometrics, 2007, 22: 747-765. [35] Aloui R, Hammoudeh S, Nguyen D K. A time-varying copula approach to oil and stock market dependence: The case of transition economies [J]. Energy Economics, 2013, 39: 208-221. [36] Reboredo J C. Modelling oil price and exchange rate co-movements [J]. Journal of Policy Modeling, 2012, 34(3): 419-440. [37] Wu C C, Chung H, Chang Y H. The economic value of co-movement between oil price and exchange rate using copula-based GARCH models [J]. Energy Economics, 2012, 34(1): 270-282. [38] Aloui R, Aïssa M S B, Nguyen D K. Conditional dependence structure between oil prices and exchange rates: A copula-GARCH approach [J]. Journal of International Money and Finance, 2013, 32: 719-738. Dynamic Dependence Between International Oil, Natural Gas and Exchange Market Based on a New Time-varying Optimal Copula Model JI Qiang1, LIU Bing-yue1, 2, FAN Ying3 (1.Center for Energy and Environmental Policy research, Institute of Policy and Management,Chinese Academy of Sciences, Beijing 100190, China; 2.Department of Statistics and Finance, University of Science and Technology of China, Hefei 230026, China; 3.School of Economics & Management, Beihang University, Beijing 100191, China) In this paper, a new time-varying optimal copula model is proposed to precisely identify the optimal dependence structure of bivariate time series at every time point. In this model, half-rotated copulas, i.e.CR1G(u,v;θ)=v-COG(1-u,v;θ) andCR2G(u,v;θ)=u-COG(u,1-v;θ), are constructed to capture the asymmetric negative dependence, especially for the negative extreme dependence, i.e. lower-upper tailτLU(α)=Pr(X tail dependence; co-movement across markets; time-varying optimal copula 2015-08-12; 2016-03-28 国家自然科学基金资助项目(91546109,71133005,71203210) 简介:范英(1966-),女(汉族),河北阳原人,北京航空航天大学经济管理学院院长,博士生导师,研究方向:能源经济学、能源市场与碳市场、能源-环境-经济系统建模等,E-mail: ying_fan@263.net. 1003-207(2016)10-0001-09 10.16381/j.cnki.issn1003-207x.2016.10.001 F830 A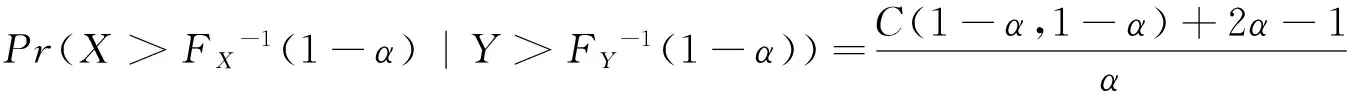

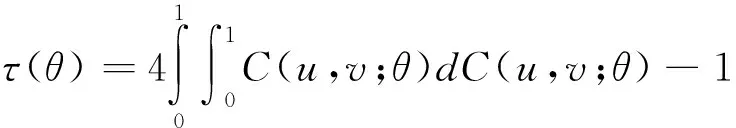


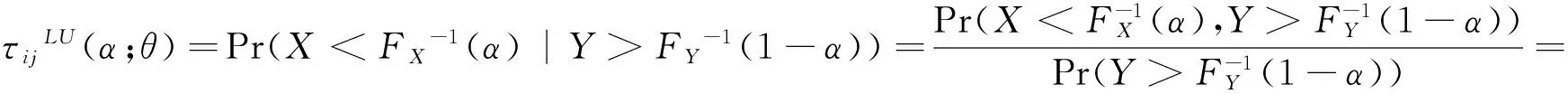




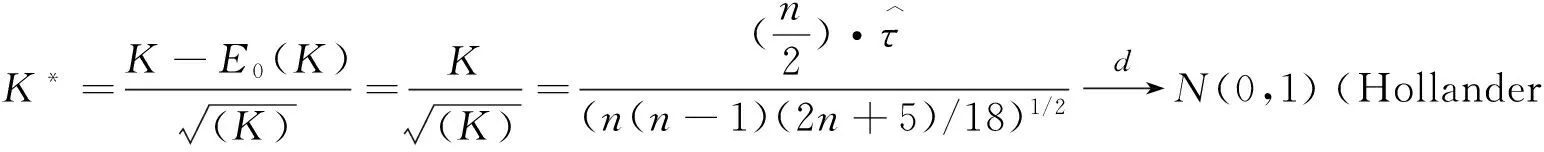

3 实证分析




4 结语
