H(curl)-椭圆问题自适应内罚间断有限元方法的收敛性分析

钟柳强, 程 婷, 邢小青

(华南师范大学数学科学学院, 广州 510631)



H(curl)-椭圆问题自适应内罚间断有限元方法的收敛性分析

钟柳强*, 程 婷, 邢小青*

(华南师范大学数学科学学院, 广州 510631)

针对H(curl)-椭圆问题的自适应内罚间断有限元方法,给出了相应的收敛性证明:把间断有限元空间分解成棱有限元空间及其正交补空间,然后结合误差的整体上界估计、关于加密网格之间的网格尺寸的2个条件以及后验误差指示子的单调性等性质,证明了在连续迭代过程中,关于误差函数的能量范数与尺度化的误差指示子之和是压缩的,即自适应内罚间断有限元方法是收敛的.

内罚间断有限元方法； 自适应算法； 后验误差指示子； 收敛性

有限元方法是现代科学计算与工程模拟中的重要数值方法之一,而间断有限元方法可视为传统(连续)有限元方法的一个发展与延拓[1-2]. 近年来,关于电磁场问题的间断有限元方法得到了学者们的重视： FEZOUI等[3]采用间断有限元的方法处理在非结构网格中时谐Maxwell 方程组问题的数值解,并得出了解收敛性以及稳定性的性质; WANG等[4]介绍了用隐式间断有限元方法求解在超材料介质中的时谐 Maxwell 方程组,并证明完全散度格式是无条件稳定的. 与此同时,自适应方法能够克服在一致加密过程中所导致自由度过度增长的情况,从而达到用最小的计算量获得较大的计算精度,但是之前关于电磁场问题的研究工作主要集中在棱有限元离散系统上,如针对变系数H(curl)-椭圆方程组和不定时谐麦克斯韦方程组,采用了一种不需要标记振荡项和加密单元不需要满足“内节点”性质的自适应棱有限元方法 (AEFEM). 并用该方法证明了 AEFEM 是收敛的[5-6].

基于间断有限元方法的特点,配合相应自适应有限元技术,能够提高计算电磁场的效率和求解精度. 本文将采用自适应内罚间断有限元方法 (AIPDG) 来求解H(curl)-椭圆问题,并研究相应的收敛性分析. 为此,首先给出连续的变分问题和相应内罚间断有限元方法离散变分系统,然后简介自适应有限元算法的每一个模块(其中后验误差估计的构造借鉴了文献[7]的思想),最后通过间断有限元空间的分解、误差的整体上界估计以及后验误差指示子的性质等,证明了自适应内罚间断有限元方法的收敛性,即在连续迭代过程中,关于误差函数的能量范数与尺度化的误差指示子之和是压缩的.

在本文中,除了特殊的常数外,为了避免重复使用一般的常数记号,采用记号、和≈，即当存在正常数C1、C2和C3,满足x1≤C1y1,x2≥C2y2,x3≤y3≤C3x3成立时,则简记为x1y1,x2y2,x3≈y3.

1 模型问题及有限元离散

本节给出连续的变分问题、间断有限元空间和若干记号，通过引入提升算子,得到了2种等价的离散变分形式.

1.1 连续变分问题

令Ω为3上的一个有界连通的多面体区域,其边界为∂Ω, n表示∂Ω上的单位外法向量. 本文研究如下H(curl;Ω)椭圆问题：

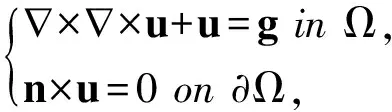
(1)

其中g(L2(Ω))3可表示为给定电磁场外源函数. 模型问题(1)可应用于几类经典电磁场问题的数值模拟,如描述涡流模型[8]、描述时域电磁场问题[9],对该问题进行相关研究具有一定的实际应用价值.

令L2(Ω)表示定义在Ω上的L2可积函数的集合. 引入如下标准的Sobolev空间：

H0(curl;Ω)={u(L2(Ω))3:×u(L2(Ω))3,

n×u=0 on ∂Ω}.

此时可得到模型问题(1)的连续变分问题:求uH0(curl;Ω),满足:

a(u,v)=(g,v) (∀vH0(curl;Ω)),

(2)

其中

a(u,v)=∫Ω((×u),(×v)+uv)dx,(g,v)=∫Ωgvdx.注意到双线性型a(·,·)是对称正定的,从而利用Lax-Milgram定理可知连续变分问题(2)是适定的.

1.2 有限元空间及若干定义

定义如下间断有限元空间:

Vh={v(L2(Ω))3:vT=v∣T(Pl(T))3,∀Th},

其中Pl(T)表示的是定义在T上次数不超过l的多项式集合,l≥1是某一个给定的整数.

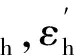
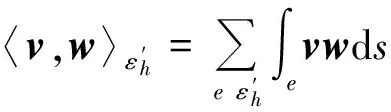
‖v‖Σh,‖v‖.

定义分片Sobolev函数空间

H1(Ω,h)={vL2(T):vT=v∣TH1(T),∀Th}.

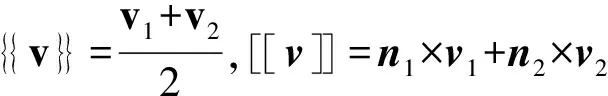
若e,则必仅存在某一个剖分单元Th,满足e∂T,此时定义:{{v}}=vT,[[v]]=n×vT,v(H1(Ω,h))3.

1.3 离散变分形式

与模型问题(1)相对应的对称内罚间断有限元方法为[10]:求uhVh,满足

aIP(uh,vh)=(g,vh)(∀vhVh),

(3)

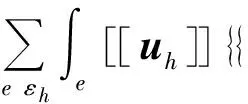
(4)

其中常数μ≥0表示内罚参数,he表示面e上的直径.

为了将式(4)的平均项和跳跃项上的部分面积分改写为体积分形式,需要引入提升算子[11-12],进而得到双线性型aIP(·,·)的另一等价形式ah(·,·).

∫Ωh(v)·wdx=<[[v]],{{w}}>εh(∀wVh).

(5)

引理1[12]4685存在一个仅依赖网格形状正则和多项式次数有关的常数CL，使得

‖h(v)‖L2(Ω)≤CL‖‖L2(εh).

定义在(H1(Ω,h))3×(H1(Ω,h))3的双线性型ah(·,·)和 泛函Fh(·)如下:ah(w,v)=(×w,×v)+(w,v)-(h(w),×v)-

(6)

和

Fh(v)=(g,v)(∀v(H1(Ω,h))3).

利用式(5),并比较式(4)和式(5),容易得到

ah(uh,wh)=aIP(uh,wh) (∀uh,whVh).

由此,可得到离散变分问题(3)的另一个等价形式,求uhVh,满足

ah(uh,vh)=Fh(vh) (∀vhVh).

(7)

在函数空间(H1(Ω,h))3上定义依赖于网格的能量范数:

(8)

下面的引理给出了ah(·,·)的连续性和强制性,其中关于连续性可参见文献[13]131的引理4.2,关于强制性可以参见文献[12]4686的式(15).

ah(w,v)≤Ccont‖w‖h‖v‖h(∀w,vVh),

(9)

同时存在常数μ0和Ccoer，使得对于μ≥μ0,有强制性结论:

ah(v,v)≥Ccoer‖v‖(∀vVh).

(10)

利用引理2及Lax-Milgram定理可证明离散变分问题(7)的解是存在且唯一的.

注2 为保证式(10)的强制性,μ需假设足够大. 值得注意的是本文证明 AIDPG 方法的收敛性时,对μ仍然需要假设足够大(见定理1).

注3 由引理2可知:ah(·,·)≈‖·‖,即双线性型形式与能量范数是等价.

2 自适应间断有限元法

自适应有限元方法的一般流程为[14]497:求解→估计→标记→加密.

uh=SOLVE(h,g).

本文总假设上述所求得的有限元解是精确的.

基于文献[7]的后验误差估计的设计思想,定义如下一种基于残量型的后验误差估计指示子,即对于任意的单元Th,eεh,在单元上的误差指示子为:

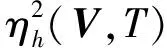
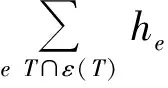
(11)

注意到由网格的形状正则有hT≈he(即它们是相容的).

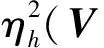
(12)

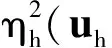
k+1=REEINE(k,k)

3 收敛性分析

本节首先给出间断有限元空间的分解及相关预备知识,然后利用误差的整体上界估计及后验误差指示子的性质等,证明了自适应内罚间断有限元方法的收敛性.

离散有限元空间Vh可分解为协调有限元空间和非协调有限元空间,即利用能量内积的正交分解,有

Vh⊕,

(13)

引理3(局部正交性)[7]19令uH0(curl;Ω)和uhVh分别是式(2)、(7)的解,则如下局部 Galerkin 正交性成立:

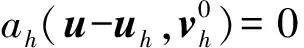
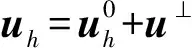
‖‖hμ1/2‖‖εh.

(14)

引理5[7]20令uhVh是式(7)的解,则存在一个常数μ1>μ0,其中μ0为引理2所给出的常数,对任意的μ>μ1,有

引理6[7]21令uH0(curl;Ω)和uhVh分别是式(2)和式(7)的解,存在一个由引理5所给出的常数μ1,使得对任意的μ>μ1,有

ah(u-uh,u-uh)≤CUη2(uh,h).

(15)

在给出自适应内罚间断有限元方法的收敛性之前,需要先介绍如下2个条件.

条件1 对1个单元剖分成2个单元的过程叫做单元加密,该过程由初始网格剖分0以及加密原则所决定. 如果T′是Th的细分,则存在常数0<βm≤βM<1满足βmhT≤hT′≤βMhT. 而且0上任意的加密剖分h的形状规则由0决定.

对于上述的自动加密满足的性质与剖分形式无关,因为对于加密单元的形状正则是保留上述性质的. BINEV等[16]讨论了依赖于初始标记0的加密剖分的情形,对于更多情形的讨论可参见文献[17].

事实上,对任意的eεh,必存在某一个Th，满足e∂T,且由网络的形状正则性有he≤ChT. 同理，对任意e*εh*,如存在某一个T*h*，满足e*∂h*及hT*≤Che*,特别地，若e*e,则T*由T加密得到，因此由条件1有：hThT*，从而证得he≤ChThT*≤Che*.

利用误差指示子的定义(12)和条件2,容易得到如下误差指示子的单调性.

ηh*(V,h*)≤ηh(V,h) (∀VVh).

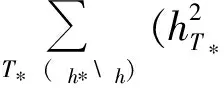
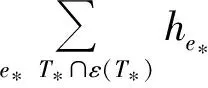
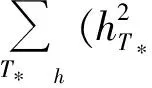
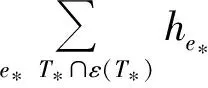
再两边开方即证得结论.

(1+ζ-1)Cer(‖×(V*-V)‖‖V*-V‖).

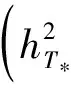
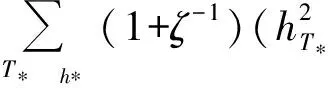
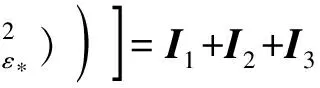
(16)

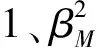
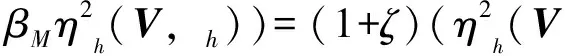
(17)

然后估计I2. 事实上,利用迹不等式及hT(0,1),则≤hT，从而可得:

I2‖×(V-V*)‖

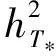
(18)

(19)

把式(17)～(19)代入式(16),则证得所需结论.

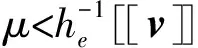
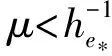
(h(v),‖h(v)‖T‖×v‖T≤

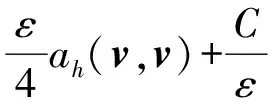
(20)

ah*(v,v)≤ah(v,v)+

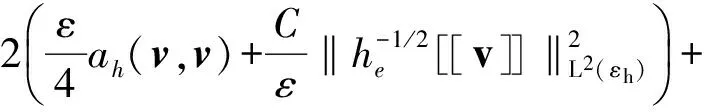
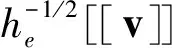
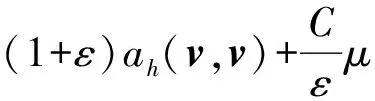
结论得证.

ah*(u-uh*,u-uh*)≤(1+ε)ah(u-uh,u-uh)-

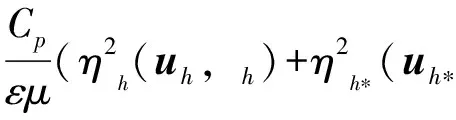
(21)

ah*(u-uh*,u-uh*)=

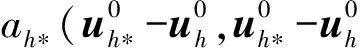
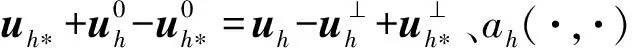
ah*(u-uh*,u-uh*)≤ah*(u-uh,u-uh)-

Ccoer(‖‖‖‖

Ccont‖‖

(22)

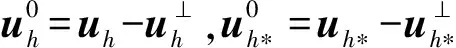
(23)

把式(23)代入到式(22),并且运用Young’s不等式可得:

a(u-uh*,u-uh*)≤(1+ε)a(u-uh,u-uh)-

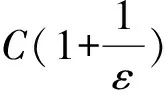
(24)

此处ε(0,1). 利用三角不等式和式(14),可得:

‖‖μ‖‖

(25)

最后把式(25)代入式(24),并利用引理9 (其中令vh=u-uh(H1(Ω,h))3),即证得本引理的结论.

有了上述准备工作,下面给出自适应内罚间断有限元方法的收敛性证明.

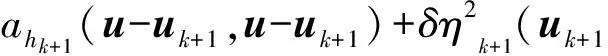
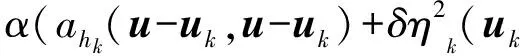
(26)

证明 为了推导过程的书写方便,简记Eku-uk、ak(·,·)a(·,·)和ηkη(uk,k)分别为自适应算法中第k步的误差、双线性型和误差估计指示子.

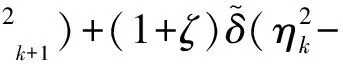
(27)

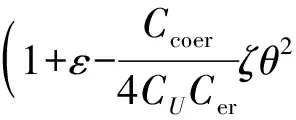
(28)

为简化系数,引入记号:Λ1)和Λ2,则式(28)简化为:

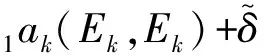
(29)

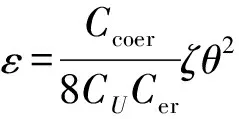
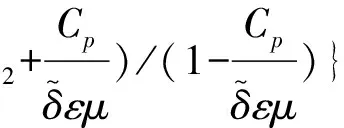
推论1 在定理1的假设条件下,有

‖u-uk‖≤CΞ,

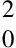
证明 利用强制性(10)以及定理1可知:Ccoer‖u-uk‖

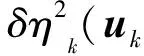
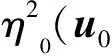
αk(Ccont‖u-u0‖,0)).

(30)

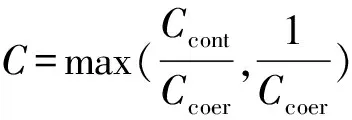
‖u-uk‖,

推论1表明,对于任意给定的充许误差精度,自适应内罚间断有限元方法总会在有限步内达到.

[1] RIVIERE B. Discontinuous Galerkin methods for solving elliptic and parabolic equations:theory and implementation[M]. Philadelphia:Society for Industrial and Applied Mathematics,2008.

[2] 张铁. 间断有限元理论与方法[M]. 北京：科学出版社,2012.

[3] FEZOUI L,LANTERI S,LOHRENGEL S,et al. Convergence and stability of a discontinuous Galerkin time-domain method for the 3D heterogeneous Maxwell equations on unstructured meshes[J]. Esaim Mathematical Modelling & Numerical Analysis,2005,39(6):1149-1176.[4] WANG J X,XIE Z Q,CHEN C M. Implicit DG method for time domain maxwell’s equations involving metamaterials[J]. Advances in Applied Mathematics and Mechanics,2015,7(6):796-817.

[5] ZHONG L Q,SHU S,CHEN L,et al. Convergence of adaptive edge finite element methods forH(curl)-elliptic problems[J]. Numerical Linear Algebra with Applications,2010,17(2/3):415-432.

[6] ZHONG L Q,CHEN L,SHU S,et al. Convergence and optimality of adaptive edge finite element methods for time-harmonic Maxwell equations[J]. Mathematics of Computation,2012,81(278):623-642.

[7] 邢小青,钟柳强.H(curl)-椭圆问题不连续 galerkin 法的后验误差估计[J]. 华南师范大学学报(自然科学版),2012,44(3):18-21.

XING X Q,ZHONG L Q. A posteriori error estimate of discontinuous Galerkin methods forH(curl)-elliptic problems[J]. Journal of South China Normal University(Natural Science Edition),2012,44(3):18-21.[8] BOSSAVIT A. Computational electromagnetism:variational formulation,complementarity,edge elments[M]. San Diego,CA:Academic Press,1998.

[9] HIPTMAIR R. Multigrid method for Maxwell’s equations[J]. SIAM Journal on Numerical Analysis,1999,36(1):204-225.

[10]ARNOLD D. An interior penalty finite element method with discontinuous elements[J]. SIAM Journal on Numerical Analysis,1982,19(4):742-760.

[11]BASSI F,REBAY S. A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations[J]. Journal of Computational Physics,1997,131(2):267-279.

[12]PERUGIA I,SCHOTZAU D,MONK P. Stabilized interior penalty methods for the time-harmonic maxwell equations[J]. Computer Methods in Applied Mechanics and Engineering,2002,191(41-42):4675-4697.

[13]HOUSTON P,PERUGIA I,SCHOTZAU D. An a posteriori error indicator for discontinuous galerkin discretizations ofH(curl)-elliptic partial differential equations[J]. IMA Journal of Numerical Analysis,2007,27(1):122-150.

[14]NOCHETTO R H,SIEBERT K G,VEESER A. Theory of adaptive finite element methods:an introduction[M]∥DEVORE R,KUNOTH A. Multiscale,nonlinear and adaptive approximation. Berlin:Springer,2009:409-542.

[15]DORFLER W. A convergent adaptive algorithm for poisson’s equation[J]. SIAM Journal on Numerical Analysis,1996,33(3):1106-1124.

[16]BINEV P,DAHMEN W,DEVORE R A. Adaptive finite element methods with convergence rates[J]. Numerische Mathematik,2004,97(2):219-268.

[17]BANSCH E. Local mesh refinement in 2 and 3 dimensions[J]. Impact of Computing in Science and Engineering,1991,3(3):181-191.

【中文责编：庄晓琼 英文责编：肖菁】

Convergence of Adaptive Interior Penalty Discontinuous Galerkin Methos for H(curl)-Elliptic Problems

ZHONG Liuqiang*, CHENG Ting, XING Xiaoqing*

(School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China)

The convergence of Adaptive Interior Penalty Discontinuous Galerkin methos (AIPDG) forH(curl)-elliptic problem is proved. To this end, the discontinuous finite element space is decomposed into the edge finite element and the corresponding orthogonal space, then the global upper bound, two conditions for the meshsizes between the refinement procedure, and the property of the error of estimator are established and combined. At last, the AIPDG is proved to be a contraction, for the sum of the norm of energy error estimation and the scaled error indicator, between two consecutive adaptive loops; namely, AIPDG is convergent.

Interior Penalty Discontinuous Galerkin method; adaptive algorithm; the error of estimator; convergence

2016-06-29 《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(11671159);广东省自然科学基金项目(2016A030313842);全国博士学位论文作者专项资金项目(201212);广东省高等学校优秀青年教师培养计划专项(Yq2013054);广州市珠江科技新星项目(2013J2200063)

O241.82

A

1000-5463(2016)05-0092-07

*通讯作者:钟柳强,教授,Email:zhong@scnu.edu.cn;邢小青,副教授,Email:xingxq@scnu.edu.cn.