基于反泄漏Fourier变换的地震数据重建方法
2016-12-02王天野白军辉王维红贺旎妮宋元东井洪亮
王天野, 白军辉, 王维红, 贺旎妮, 宋元东, 井洪亮
( 1. 东北石油大学 地球科学学院,黑龙江 大庆 163318; 2. 大庆油田有限责任公司 第三采油厂,黑龙江 大庆 163113; 3. 北京大学 地球与空间科学学院,北京 100871; 4. 东方地球物理公司 吐哈物探处,新疆 哈密 839009 )
基于反泄漏Fourier变换的地震数据重建方法
王天野1, 白军辉2, 王维红1, 贺旎妮3, 宋元东1, 井洪亮4
( 1. 东北石油大学 地球科学学院,黑龙江 大庆 163318; 2. 大庆油田有限责任公司 第三采油厂,黑龙江 大庆 163113; 3. 北京大学 地球与空间科学学院,北京 100871; 4. 东方地球物理公司 吐哈物探处,新疆 哈密 839009 )
应用反泄漏Fourier重建方法,对空间方向采样不规则的地震数据进行规则化重建,引入GPU加速算法,将非均匀Fourier变换部分转化为矩阵乘法形式,将矩阵乘法部分应用于GPU加速算法加速处理。理论模型与实际数据测试结果验证该方法的有效性及合理性。
数据重建; 规则化; Fourier变换; GPU; 地震数据采集
0 引言
在地震数据采集过程中,通常受障碍物、禁采区、海洋拖缆羽状漂移影响及经济条件等制约。地震数据在空间方向上的采集通常是稀疏的或不规则的,对后续偏移及多次波处理等产生影响。因此,对地震数据进行合理化重建、规则地震数据及合理恢复稀疏道尤为重要。
目前,基于变换域重建的地震数据重建方法分为Radon变换重建、Fourier变换重建及Curvelet变换重建。这类方法一般将数据进行正变换,在变换域中根据信号特点进行相应处理;再通过反变换将数据变换到原始数据域,通过正反变换实现地震数据重建。第一步,将数据以恰当的形式正变换估算得到变换域的系数。假使数据是不规则的,那么正变换计算得到的系数可能是不精确的。第二步,通过反变换合理重建理想规则数据。基于变换域的重建方法的优势是计算速度快,对输入数据可以在一定程度上稀疏采样,既可以较好地处理规则采样数据,又可以对非规则采样数据进行合理重建。当地震是有限带宽时重建效果更好。Fourier变换重建技术已经成功应用于一维、二维非规则采样数据重建。Duijndam A J W等[1]采用分频谱反演方法估计空间Fourier系数,并成功将Fourier重建方法应用于非规则采样地震数据的规则化问题和三维数据重建[2],可以解决参数选择等问题,但存在空间假频的地震数据而使重建效果变差。Liu B等[3]提出最小加权范数插值的Fourier重建方法,虽然可以对所得解进行优化,但没有解决数据存在假频的情况。孟小红[4]等将带限地震数据的重建归结为最小二乘反演问题,并将非均匀离散Fourier变换变为非均匀快速Fourier变换[5],有效提高计算效率,但抗假频能力不足。刘喜武等将非均匀Fourier变换与预测滤波方法结合,以解决抗假频重建问题[6]。高建军[7]等应用抗泄漏Fourier变换方法,有效解决不规则地震道假频问题,并结合贝叶斯反演对三维地震数据进行重建。Xu S[8]等应用过采样技术及权值求取方法,消除吉布斯现象及假频影响,并给出二维切片形式,以重建三维数据体。
CPU/GPU协同并行加速技术被广泛应用于地震处理的各个领域。如在多次波预测中,通过应用GPU加速处理矩阵乘法部分[9],可以大幅提高处理速度。在叠前偏移[10~13]及全波形反演中[14],GPU加速技术的应用使得数据的处理变得更为方便快捷。基于反泄露Fourier变换方法,笔者应用CPU/GPU并行加速算法提高运算效率,并验证方法的合理性和有效性。
1 方法原理
反泄漏Fourier变换的目的是对不规则地震数据进行重建,并能够压制波数域谱泄漏。由于时间方向是规则采样,因此可以应用FFT将时间域数据变换到频率域数据,以提高计算效率。在不规则网格中,单个频率的反泄漏Fourier变换公式[11]可以表示为
(1)
(2)
式(1-2)中:F(k)为波数k的Fourier系数;xn为采样点,ΔX=∑Δxn;Np为输入点的个数;fk(xl)为k的Fourier系数对采样点xn的函数值贡献。对于不规则数据,由于正交性被破坏,fk(xl)能量泄漏到其他频率成分中。
为了消除谱泄漏现象,首先对所有Fourier系数进行估计,确定最大能量及其对应位置;然后反变换到输入数据网格中,从原始数据中去除最大能量对应的贡献值,得到更新后的输入数据并反复迭代;最终得到消除谱泄漏的规则化数据。
去除表达式为
(3)
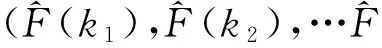
规则化重建表达式为
(4)
2 优化反泄漏算法
将反泄漏Fourier变换算子及输入数据拆分成矩阵相乘形式,并从主机端输入到GPU端,根据分块线程原则和矩阵乘法在GPU中的计算方法,合理分配内存及赋值处理。该算法原理见图1。

图1 GPU棋盘划分矩阵乘法流程示意Fig.1 GPU board division matrix multiplication process
将反泄漏变换公式拆分,正反变换矩阵相乘形式为
(5)
(6)
式(5-6)中:offset[i]为空间方向不规则采样间隔;offsetinter[i]为规则化后空间方向的采样间隔;dk为波数方向的采样间隔。
在科学计算方面,GPU具有高速度、高性能及较高的并行计算效率。利用GPU加速计算NDFT运算的矩阵乘法、GPU提供的CUFFT(基于CUDA语言的快速Fourier变换)函数库,以及乘除开方等快速计算函数优化算法指令,提高地震数据重建算法效率。
由图1可以看出,该方法对全局存储器的数据依次按照线程ID号,将A块数据依次放入BLOCK对应的共享存储器;然后BLOCK中每个Thread按照索引计算一个Csub,进行多次循环,每次循环后将数据加到上次循环得到的Csub上,直到所有数据在共享存储器中得到计算并将获得结果相加;最后得到的求和即为(0,0)块结果。
3 理论模型与实际数据测试
3.1 理论模型测试
为了测试文中算法的有效性,抽取多炮复杂Smaart模型单炮并进行模型试算,去除单炮数据部分道信息并进行抽稀处理,将数据变为非均匀采样形式(见图2)。该数据空间方向为361道,道间距为75 m,时间方向采样率为0.008 s。空间方向上随机抽出22道,最大道间距为225 m(见图2(a)),缺失道重建后成图(见图2(b))。其中不规则数据f-k谱见图2(c),规则化后数据f-k谱见图2(d)。
由图2(a)、(b)可以看出,经过文中算法处理后,图像缺失道数据的缺失信息得到有效补偿,重建后图像清晰、误差小,补偿后图像光滑连续,符合实际数据图形走向。由图2(c)、(d)可以看出,不规则缺失数据造成的能量泄露现象得到有效压制,能量收敛,波数方向0.3~0.4 m-1部分能量回归到有效能量中。规则化后f-k谱有效能量集中在小视速度范围内。因此,该算法对于复杂数据具有很好的恢复效果。


图2 Smaart模型理论数据测试结果Fig.2 Smaart model theoretical data test results
3.2 实际数据测试
为了验证该算法对复杂数据的适用性,对某油田海上叠前实际数据进行处理(见图3)。该数据道间距为20 m,共计800道。由于数据道数较大,对数据进行去除和前后统一处理,保留前200道。在规则的200道数据中随机抽出40道数据,其中最大道间距为60 m,抽稀后不规则数据见图3(a)。对去除后数据进行规则化处理,缺失道数据得到有效补偿,重建后规则数据见图3(b)。重建前f-k谱见图3(c),重建后f-k谱见图3(d)。
由图3可以看出,应用文中算法对复杂叠前不规则数据进行规则化重建,重建前、后时域数据中缺失道信息得到有效补偿,恢复后图像同相轴连续,与原始图像对比误差较小。f-k谱泄漏能量收敛,视速度较大部分的泄漏能量回归到有效能量中,有效部分能量集中在视速度较小位置。


图3 某油田海上叠前实际数据测试结果Fig.3 Test results for real data of oilfield
3.3 数据加速比
为测试基于CUDA的反泄漏地震数据重建算法的性能,在LINUX操作平台上应用C语言、结合CUDA语言编写程序,并进行测试。算法测试环境硬件参数见表1。
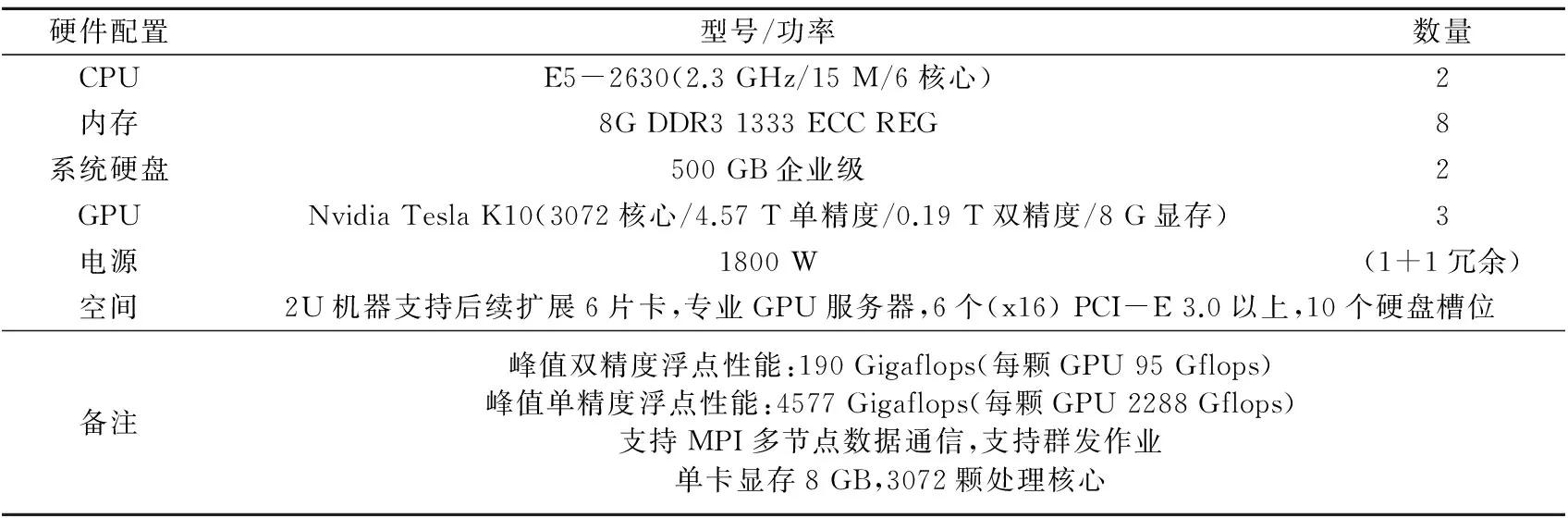
表1 算法测试环境硬件参数
采用文中算法分别对Smaart模型、叠前实际数据进行测试,得到程序运行加速比,将运行平均时间作为最后的运算时间,将最后的运算时间作为性能分析的依据。反泄漏离散Fourier变换部分分别应用CPU及CPU/GPU并行处理,两种数据在CPU上实现的总计算时间与在GPU上实现的总计算时间见表2,其中CPU运行时间与GPU运行时间之比为加速比。由表2可以看出,基于CUDA的反泄漏并行算法的有效性,程序在原基础上得到20~40倍的性能提升,数据处理的加速效果明显,在共享存储器中计算还可以将算法效率提升1.5倍。

表2 算法CPU和CPU/GPU程序测试运行时间
4 结论
(1)基于反泄漏Fourier变换的叠前地震数据规则化算法,可以对非规则网格采样数据进行规则化处理,对采样缺失数据进行插值重建,从而满足后续算法对规则网格数据的要求。应用CPU/GPU协同并行加速算法可以对不规则数据进行加速处理,对不规则及稀疏数据进行有效重建。该算法准确、易于实现,重建效果误差小、精度高,能够满足工业化处理需求。
(2)通过引用CPU/GPU协同并行加速算法,该算法将CPU中反复处理的乘法加法过程拆分成多线程运算形式并进行处理,在运算过程中大幅减少算法的时间复杂度,在大数据及三维数据中存在实现的可能性。
[1] Duijndam A J W, Schonewille M A, Hindriks C O H. Reconstruction of band-limited signals, irregularly sampled along one spatial direction [J]. Geophysics, 1999,64:524-538.
[2] Hindriks K, Ajw. D. Reconstruction of 3D seismic signals irregularly sampled along two spatial coordinates [J]. Geophysics, 2000,65(1):253-263.
[3] Liu B, Sacchi M D. Minimum weighted norm interpolation of seismic records [J]. Geophysics, 2004,69(10):1560-1568.
[4] 孟小红,郭良辉,张致付,等.基于非均匀快速傅里叶变换的最小二乘反演地震数据重建[J].地球物理学报,2008,51(1):235-241.
Meng Xiaohong, Guo Lianghui, Zhang Zhifu, et al. The nonuniform fast Fourier transform least square inversion of seismic data reconstruction based on [J]. Chinese Journal of Geophysics, 2008,51(1):235-241.
[5] Duijndam A J W, Schonewille M A. Nonuniform fast Fourier transform [J]. Geophysics, 1997,64(2):551.
[6] 刘喜武,刘洪,刘彬.反假频非均匀地震数据重建方法研究[J].地球物理学报,2004,47(2):299-305.
Liu Xiwu, Liu Hong, Liu Bin. Study on the reconstruction method of the non uniform seismic data in the anti false frequency [J]. Journal of Geophysics, 2004,47(2):299-305.
[7] 高建军,陈小宏,李景叶.三维不规则地震数据重建方法[J].石油地球物理勘探,2011,46(1):40-47.
Gao Jianjun, Chen Xiaohong, Li Jingye. Seismic data reconstruction method for 3D seismic data [J]. Oil Geophysical Prospecting, 2011,46(1):40-47.
[8] Xu S, Zhang Y, Lambaré G. Antileakage Fourier transform for seismic data regularization in higher dimensions [J]. Geophysics, 2010,75(4):87.
[9] 石颖,王维红,李莹,等.基于波动方程三维表面多次波预测方法研究[J].地球物理学报,2013,56(6):2023-2032.
Shi Ying, Wang Weihong, Li Ying, et al. Study on multi wave prediction method for 3D surface based on wave equation [J]. Journal of Geophysics, 2013,56(6):2023-2032.
[10] Clapp R G, Fu H, Lindtjorn O. Selecting the right hardware for reverse time migration [J]. Leading Edge, 2010,29(29):48-58.
[11] Knibbe H, Mulder W A, Oosterlee C W, et al. Closing the performance gap between an iterative frequency-domain solver and an explicit time-domain scheme for 3D migration on parallel architectures [J]. Geophysics, 2014,79(2):47-61.
[12] 郭雪豹,王建民,王维红,等.基于GPU并行加速的VSP数据逆时偏移[J].东北石油大学学报,2014,38(2):58-62.
Guo Xuebao, Wang Jianmin, Wang Weihong, et al. Reverse time migration of VSP data based on GPU parallel acceleration [J]. Journal of Northeast Petroleum University, 2014,38 (2):58-62.
[13] 田东升,王云专,李义鹏,等.单程和双程波动方程叠前深度偏移方法[J].东北石油大学学报,2014,38(4):39-44.
Tian Dongsheng, Wang Yunzhuan, Li Yipeng, et al. Journal of one-way and two-way wave equation prestack depth migration method [J]. Northeast Petroleum University, 2014,38(4):39-44.
[14] Yang P, Gao J, Wang B. A graphics processing unit implementation of time-domain full-waveform inversion [J]. Geophysics, 2015,80(3):31-39.
2016-07-07;编辑:任志平
黑龙江省自然科学基金面上项目(D2015011)
王天野(1992-),男,硕士研究生,主要从事地震资料数字处理方面的研究。
王维红,E-mail: wwhsy@sina.com
P631.4+14
A
2095-4107(2016)05-0102-06
DOI 10.3969/j.issn.2095-4107.2016.05.012
