n次微分分次Poisson模范畴*

吴学超,朱 卉,陈淼森

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)



n次微分分次Poisson模范畴*

吴学超,朱 卉,陈淼森

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

给出了左n次微分分次Poisson模的定义.令A是n次微分分次Poisson代数,根据A构造了一个新的微分分次代数B.同时证明了A上的左n次微分分次Poisson模范畴同构于B上的左微分分次模范畴.

微分分次Poisson代数;微分分次Poisson模;微分分次代数;李代数

0 引 言

Poisson代数的概念起源于Poisson几何,它可以简单地看成交换代数和李代数的结合.近年来,Poisson代数得到了很多不同形式的有趣的推广[1-7],例如分次Poisson代数[1]和双Poisson代数[2]等.文献[3]定义了n次微分分次Poisson代数，这类代数可以粗略地看成微分分次代数和n次微分分次李代数的结合.受此启发,本文提出了左n次微分分次Poisson模的概念.

本文的主要结果如下:

定理1 令(A,5,{,}A,dA)是n次微分分次Poisson代数,那么

1)可以构造另一个代数Ae,它是微分分次代数.定义

其中,a,b∈A为齐次元.

2)设DGP(A)为A上左n次微分分次模范畴,DG(Ae)为Ae上左微分分次模范畴，则

DGP(A)≅DG(Ae).

1 左n次微分分次Poisson模

本节将给出左n次微分分次Poisson模的定义.

定义1[3]设(A,5)是Z-分次K-向量空间.若有K-齐次线性映射{,}:A⊗A→A,|{,}|=n满足:

1)(分次反对称性){a,b}=-(-1)(|a|+n)(|b|+n){b,a};

2)(分次Jacobi恒等式){a,{b,c}}={{a,b},c}+(-1)(|a|+n)(|b|+n){b,{a,c}},a,b,c∈A为齐次元,

则称(A,{,})为n次分次李代数.

若在此基础上,有K-线性映射d:A→A,|d|=1,满足d2=0和

则称(A,{,},d)为n次微分分次李代数.

定义2[3]设(A,·)是Z-分次代数.若

1)(A,{,})是n次分次李代数,

2)a·b=(-1)|a||b|b·a,

3){a,b·c}={a,b}·c+(-1)(|a|+n)|b|b·{a,c},

其中a,b,c∈A为齐次元,则称(A,·,{,})为n次分次Poisson代数.

若在此基础上,有K-线性映射d:A→A,|d|=1满足d2=0和

4)d(a·b)=d(a)·b+(-1)|a|a·d(b),

5)d({a,b})={d(a),b}+(-1)(|a|+n){a,d(b)},

则称(A,·,{,},d)为n次微分分次Poisson代数.

定义3 令(A,·,{,},d)是n次微分分次Poisson代数,称

为A上的左n次微分分次Poisson模,如果M满足以下条件:

1)(M,*,∂)是微分分次代数A上的左微分分次模,等价于

①有K-双线性映射_*_:A⊗M→M,|_*_|=0,使得M在A上是左分次模,即Ai*Mj⊆Mi+j,i,j∈Z;

②有K-线性映射∂:M→M,|∂|=1,满足∂2=0且

其中:a∈A为齐次元;m∈M.

2)(M,*,{,})是在n次微分分次Poisson代数上的左n次分次Poisson模,即有另一个双线性括号{,}M:A⊗M→M,|{,}M|=n,满足:

①{a,b*m}M={a,b}A*m+(-1)(|a|+n)|b|b*{a,m}M;

②{a5b,m}M=a*{b,m}M+(-1)|a||b|b*{a,m}M;

③{a,{b,m}M}M={{a,b}A,m}M+(-1)(|a|+n)(|b|+n){b,{a,m}M}M.

其中:a,b∈A为齐次元;m∈M.

3)线性映射∂作用于{,}M,即

其中:a∈A为齐次元;m∈M.

记(M,*,{,}M,∂)为A上的左n次微分分次Poisson模.

注1 类似可以定义右n次微分分次Poisson模.

2 定理1的证明

为简便起见,在不引起混淆的情形下常省去下标,所取的元素都是对应代数中的齐次元.

要证明定理1,需要证明以下引理.

引理1Ae是微分分次代数.

证明 根据Ae的构造,容易看出Ae是Z-分次代数.令∂:Ae→Ae是线性映射,|∂|=1,

其中,a∈A为齐次元,使得分次莱布尼茨法则成立,即

则以上定义满足M的Ae-模构造.事实上,取a,b∈A为齐次元,x∈M,有

mab5x=(ab)5x=a(bx)=(mamb)x;

hab5x={(ab),x}M=a{b,x}M+(-1)|a||b|b{a,x}M=mahbx+(-1)|a||b|mbhax=

(mahb+(-1)|a||b|mbha)5x;

m{a,b}5x={a,b}A5x={a,bx}M-(-1)(|a|+n)|b|b5{a,x}M=

{a,mbx}M-(-1)(|a|+n)|b|mbhax=hambx-(-1)(|a|+n)|b|mbhax=

(hamb-(-1)(|a|+n)|b|mbha)5x;

h{a,b}5x={{a,b}A,x}M={a,{b,x}M}M-(-1)(|a|+n)(|b|+n){b,{a,x}M}M=

(hahb-(-1)(|a|+n)(|b|+n)hbha)x.

所以,M是左微分分次模.又由于

∂(ma5x)=∂(a5x)=d(a)5x+(-1)|a|a5∂(x)=md(a)5x+(-1)|a|ma5∂(x)=

∂(ma)5x+(-1)|a|ma5∂(x),

∂(ha5x)=∂({a,x}M)={d(a),x}M+(-1)(|a|+n){a,∂(x)}=

hd(a)5x+(-1)(|a|+n)ha5∂(x)=∂(ha)5x+(-1)(|a|+n)ha5∂(x),

所以,M是Ae上的左微分分次模.引理2证毕.

引理3 令(A,*,{,}A,d)是n次微分分次Poisson代数,且(M,∂)是Ae上的左微分分次模,那么M可以看成是A上的左n次微分分次Poisson模.

证明 ∀a∈A为齐次元,x∈M,定义

下证(M,*,{,}M,∂)是A上的左n次微分分次Poisson模.

事实上,∂:M→M,|∂|=1,满足∂2=0.取a,b∈A为齐次元,x∈M,有

∂(a*x)=∂(max)=∂(ma)5x+(-1)|a|ma5∂(x)=md(a)5x+(-1)|a|ma5∂(x)=

d(a)*x+(-1)|a|a*∂(x);

{a,b*x}M={a,mbx}M=hambx=(m{a,b}A+(-1)(|a|+n)|b|mbha)5x=

{a,b}A*x+(-1)(|a|+n)|b|b*{a,x}M;

{ab,x}M=hab5x=(mahb+(-1)|a||b|mbha)5x=a*{b,x}M+(-1)|a||b|b*{a,x}M;

{a,{b,x}M}M=hahbx=(h{a,b}A+(-1)(|a|+n)(|b|+n)hbha)5x=

{{a,b}A,x}M+(-1)(|a|+n)(|b|+n){b,{a,x}M}M;

∂({a,x}M)=∂(ha5x)=∂(ha)5x+(-1)(|a|+n)ha5∂(x)=

hd(a)5x+(-1)(|a|+n)ha5∂(x)={d(a),x}M+(-1)(|a|+n){a,∂(x)}M.

引理3证毕.

证明 1)取任意齐次元ma,ha∈Ae,x∈M.由于f是左n次微分分次PoissonA-模映射,

且

2)取任意齐次元a∈A,x∈M.由于g是左微分分次Ae-模映射,

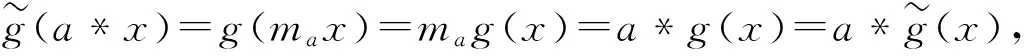
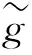
定理1的证明 由引理1可知,Ae是微分分次代数,根据引理1～4,只需证DGP(A)≅DG(Ae).

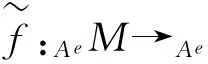
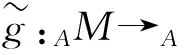
易证F和G是2个共变函子,使GF=1DGP(A)且FG=1DG(Ae),则DGP(A)≅DG(Ae).定理1证毕.

致谢：感谢吕家凤副教授的悉心指导.

[1]Cattaneo A S,Fiorenza D,Longoni R.Graded Poisson algebras[J].Enc Math Phy,2006,2(6):560-567.

[2]Van den Bereer M.Double Poisson algebras[J].Trans Amer Math Soc,2008,360(11):5711-5769.

[3]吴学超,朱卉,陈淼森.n次微分分次Poisson代数的张量积[J].浙江大学学报：理学版,2015,42(4):391-395.

[4]Beltran J V,Monterde J.Graded Poisson structures on the algebra of differential forms[J].Comment Math Helv,1995,70(2):383-402.

[5]Xu P.Noncommutative Poisson algebras[J].Amer J Math,1994,116(1):101-125.

[6]鲍炎红，李华.关于Poisson包络代数的注记[J].安徽大学学报：自然科学版,2013,37(1):23-27.

[7]Oh S Q.Poisson enveloping algebras[J].Comm Algebra,1999,5(3):2181-2186.

(责任编辑 陶立方)

The category ofn-differential graded Poisson module

WU Xuechao,ZHU Hui,CHEN Miaosen

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

The notion of a leftn-differential graded Poisson module was given.SupposedAis ann-differential graded Poisson algebra,a new differential graded algebraBwas constructed.The categories of leftn-differential graded Poisson modules overAis isomorphic to the categories of left differential graded modules overBwas proved.

graded Poisson algebras; graded Poisson module; differential graded algebra; Lie algebras

10.16218/j.issn.1001-5051.2016.01.007

��2015-06-07；

2015-09-04

国家自然科学基金资助项目(11571316)

吴学超(1990-),女,浙江义乌人,硕士研究生.研究方向：代数学.通信作者：陈淼森.E-mail:mschen@zjnu.cn

O153

A

1001-5051(2016)01-038-05