回归课本的层次与原则

乔安国+李想玲

关于高考复习，我相信同学们听得最多的一个词就是“回归课本”，但到底什么是回归课本？如何回归课本？许多人都说不出个所以然来. 下面，结合立体几何部分的高考题来谈一谈回归课本的几个层次与原则.

回归课本的四个层次

1. 通过回归课本熟记公式、定理及常用结论

高考复习尤其是第一轮复习有一个重要的任务就是查漏补缺，回归课本首先要做的就是系统地检查对相关公式、定理及常用结论的记忆是否准确、是否熟练.

答案 C

点评 本题考查空间几何体的三视图与体积，其中台体的体积公式容易忘记，会为本题的解答带来困难. 同学们在做这道题目的时候，若对台体的体积公式比较生疏，就应该回归课本，去温习一下台体的体积公式，并以此展开，系统思考一下空间几何体的体积公式的推导与记忆方法.

2. 通过回归课本构建完善的知识体系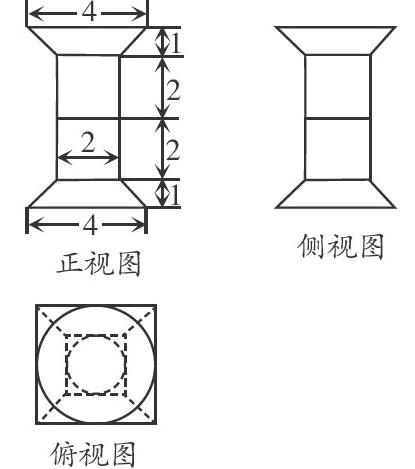

由于高中数学需要掌握的知识点很多，在有限的时间内要达到这个目标，就需要从宏观上全面系统地掌握所学知识，把握知识间的内在联系，构建起一棵知识之树，这样才能更深刻地理解所学知识，提高学习效率. 例如构建线线平行、线面平行和面面平行的关系图.

例2 如图，在三棱锥中，D，E，F分别为棱的中点. 已知求证： 直线平面.

点评 本题的目标是要证明直线平面，有两种方法可选. 一是在平面中找（作）一条直线，证明直线与这条直线平行，利用线面平行的判定定理推出直线平面；二是在图形中找（作）一个经过直线的平面，证明该平面与平面平行，利用线面平行的定义证明直线平面. 分析题中给出的条件，易证，选择第一种方法更佳.

3. 通过回归课本发掘课本中知识的生长点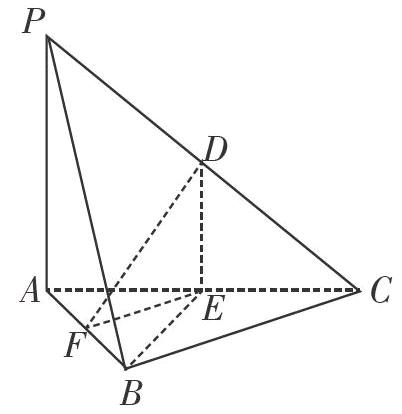

回归课本绝不是要拘泥于教材，而是在吃透教材的基础上发挥我们的主观能动性，对教材内容进行个性化的解读和处理，发现知识的生长点. 仔细分析历年来各地高考数学试题，可以发现许多考题都可以在课本中找到它的原型. 这些题都在考查基本概念、基本方法，而这些基本概念、基本方法又在我们的课本中，这样将高考数学试题源于课本又高于课本的命题原则表现得淋漓尽致. 因此回归课本的方式绝对不是单纯地看书，必须要带着一双善于发现的眼睛.

例3 如图，在棱长为2的正方体中，E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为_________.

答案

点评 本题取材于人教A版必修二第139页习题B组第3题. 这是一道探究题，在两条异面直线上分别取了一个点，探究这两个点连线距离的最小值. 在探究中，若我们能带着发现问题的眼睛，就可以同时探究一下其中一条直线上的点到另一直线的距离，这就是本例的解题方法. 进一步，我们还可以探究一下两条异面直线之间 的距离的解题方法.

例4 如图，是圆的直径，点是圆上异于的点，垂直于圆所在的平面，且.

（1）若为线段的中点，求证：平面；

（2）求三棱锥体积的最大值；

（3）若，点在线段上，求的最小值.

答案 （1）略 （2） （3）

点评 本题图形与人教A版必修二第74页习题B组第4题的图形是一样的，在分析问题时，都必须注意到这一条件的应用. 在看课本上这道习题的时候，我们完全可以将圆的各种内接多边形作为底面，在圆面外取一点（例4就是取在圆心的正上方）来构造棱锥；然后在里面研究线面平行、垂直关系的证明以及空间角度与距离的计算. 若能如此发掘，再来解答例4就是轻而易举的事情.

4. 通过回归课本提炼思想方法并加以延伸

数学课本中的习题都是经过教材编写专家们精心选择的，具有一定的典型性和代表性，不仅反映了相关数学知识的本质属性，而且还蕴含着重要的数学思想方法，对培养分析问题、解决问题的能力有着极为重要的作用.

（1）证明：平面；

（2）求直线与平面所成角的正弦值.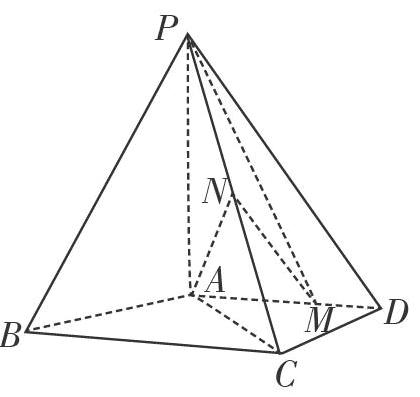

答案 （1）略 （2）

点评 本题以四棱锥为载体，四棱锥有一条侧棱与底面垂直，证明线面平行和计算直线与平面所成角的正弦；而人教A版选修2-1第109页的例4，同样是以四棱锥为载体，四棱锥有一条侧棱与底面垂直，证明线面平行、线面垂直和计算二面角的大小，两者的解题方法基本一样. 在四棱锥有一条侧棱与底面垂直的情况下，其中有哪些线面垂直？如何建立空间直角坐标系？哪些平面的法向量可以直接取？以此为载体，将相关问题的解决方法考虑清楚，就能触类旁通、举一反三.

回归课本的三个原则

1. 需要性原则

在需要的时候回归课本，不是为了回归课本而回归课本. 何时是需要的时候？在高三复习的整个阶段都是，都有需要看书的时候，而不单单是最后一个月. 当然最后一个月必须要回归课本. 何时是需要的时候？在做错题目的时候，基本知识有遗忘的时候，题目不会做的时候，归纳总结的时候等等.

2. 目的性原则

在需要性原则中，我们是在解决问题的过程中遇到困难，被动地回归课本；而目的性原则是我们有计划地主动带着问题回归课本. 回归课本的目的，要么是搞懂或者记住某个知识点，要么是为了温习某种方法，要么是为了归纳总结知识体系. 总之，回归课本必须奔着一个目的而去.

3. 实践性原则

回归课本看书时，一定要和做题结合起来. 在解题时回归课本，厘清概念、掌握方法、领会思想；在回归课本时做题，学以致用. 在经常考的地方认真看，边看书边记忆；在经常出题的地方认真做，边做题边思考；把历次考试的试卷、历年高考真题试卷、复习资料摆在课桌的右上方，觉得需要翻题目的时候就翻一下，边翻边体会. 这样我们就能把课本用活，提高备考效率.