堆石微裂缝扩展规律及其影响因素
2016-12-01迟世春
邵 磊,余 挺,迟世春
(1.中国电建集团 成都勘测设计研究院有限公司,成都 610072;2.大连理工大学 建设工程学部,辽宁 大连 116024)
堆石微裂缝扩展规律及其影响因素
邵 磊1,余 挺1,迟世春2
(1.中国电建集团 成都勘测设计研究院有限公司,成都 610072;2.大连理工大学 建设工程学部,辽宁 大连 116024)
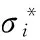
堆石料;亚临界裂缝扩展模型;颗粒破碎;应力强度因子;相对湿度
1 研究背景
在岩石断裂力学理论中,岩石是含有微缺陷和不连续节理面的材料,在外部荷载与外部环境的共同作用下,微缺陷会逐渐发展形成微裂缝[1]。微裂缝的发展受外部环境(主要是相对湿度和应力条件)、应力强度因子及其断裂韧度控制。在长时间或循环加载条件下,当裂缝尖端的应力强度因子小于其起裂韧度时,微裂缝不发展;当应力强度因子大于起裂韧度且小于断裂韧度时,裂缝以极慢的速度扩展;当应力强度因子接近或超过断裂韧度时,裂缝的扩展速度发生突变,岩石迅速断裂[1-2]。当应力强度因子小于断裂韧度时,裂缝随着时间扩展的现象被称为亚临界裂缝扩展,国内外很多学者对此展开了相关研究。如肖洪天等[3-4]采用双扭试件和自行研制的加载装置,对三峡船闸花岗岩进行了亚临界裂纹扩展的试验研究,并获得了该岩石的裂纹扩展速度与应力强度因子的关系;袁海平等[5]采用双扭试件常位移松弛法,得出金川软弱复杂矿岩亚临界裂纹扩展速度与应力强度因子之间的关系;李江腾等[6]研究了大理岩、花岗岩的裂纹扩展速率与应力强度因子的关系及断裂韧度,并确定了裂纹扩展停滞速度和门槛值。进一步地,Nare等[7-8]发现岩石裂纹扩展速度受裂纹扩展方向、蒸汽压和试件导向槽截面形式的影响,并利用应力腐蚀理论解释了蒸汽压影响亚临界裂纹扩展速度的原因。
微裂缝随时间扩展最终导致岩块破裂。这一结论在一系列岩石强度试验中岩石颗粒的破碎现象得到了证实(Wilkins(1980)[9], Wiederhorn等(1980)[10])。Oldecop等(2001,2007)[1-2]据此开展了堆石料的流变机理研究,推导了考虑流变的堆石料压缩系数,并指出堆石料流变是由于堆石颗粒破碎引起颗粒重排调整所致。这一理论对水位上升引发堆石湿化以及降雨引起堆石集中变形也给出了合理解释。这是因为岩石颗粒含水率增加会降低岩块的断裂韧度,增加裂缝的扩展速度,引起堆石料颗粒的集中破碎与重排,从而造成短期内集中变形[1-2]。但Oldecop等人没有进行堆石颗粒裂缝慢速扩展—破碎—重排的定量化研究,后期变形的机理分析亦不够深入。邵磊等[11-12]在Oldecop等(2001,2007)[1-2]研究工作的基础上,采用三维颗粒流方法模拟了筑坝堆石料受力变形中不断进行的颗粒裂缝扩展—破碎—重排—应力调整过程,探讨了堆石流变机理,为研究堆石流变性质及机理开辟了一条新途径。本文进一步开展了堆石颗粒微裂缝扩展的影响因素研究,有助于深化对堆石料微裂缝扩展规律的认识,使亚临界裂缝扩展理论在细观力学模拟中能得到更好的应用。
2 亚临界裂缝扩展计算原理
2.1 应力强度因子
Broek (1986)[13]由线弹性断裂力学得到裂缝尖端的应力强度因子Ki的计算公式,即
(1)
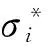
Tada等[14]给出了βi的经验公式为
(2)
式中:α=2ai/R,R为颗粒半径。
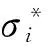
(3)
式中:A为圆柱体或者立方体的最大截面面积;P为点荷载。
曲嘉[15]通过试验研究给出了圆球体混凝土试样的劈拉强度公式为
(4)
上式可简化为
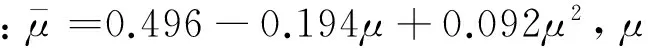
通过式(1)至式(3),可以求出含有初始裂缝i(初始半长度为ai)的圆球颗粒在对称点荷载P作用下裂缝尖端的应力强度因子Ki。
2.2 裂缝扩展速度
岩石作为一种含有缺陷的脆性材料,其破坏过程实质上就是微裂纹产生、扩展及贯通的过程,应力腐蚀机制能很好地说明亚临界裂纹的扩展[1]。在建立岩石类材料裂纹亚临界扩展速度关系时,通常考虑裂纹扩展速度与裂纹尖端的应力强度因子之间的关系,其中适合岩石材料的应力腐蚀理论是Charles理论[16],最通用的Charles方程为
(5)
式中:Vi为裂纹扩展速度;E*为活化焓(热力学函数);a为裂纹长度;t为时间;R0为气体常数;T为绝对温度;v0,n为材料属性。
当温度T恒定时,可将Charles方程表示为K-V空间的幂函数和lgK-lgV空间的线性函数,即
(6)
式中:A,a,b均为常数;A=10a;b=n,称之为应力腐蚀因子或亚临界裂纹扩展指数。通常将岩石加工成规则形状试件,利用双扭试件测试获得岩石亚临界裂纹扩展Charles理论的相关参数。如肖洪天等[3-4]从三峡永久船闸工地取回的花岗岩岩芯,经切割、磨平,加工成双扭试件,从而测得其裂缝扩展参数A,n,以及断裂韧度Kc。
此外,Charles(1958)[16]还通过拟合大量材料的应力腐蚀试验曲线,得到描述裂缝扩展速度Vi与应力强度因子Ki的经验公式,即
(7)
式中V0是材料属性。
2.3 裂缝扩展计算原理
根据式(7),处于亚临界扩展状态的裂缝,其半长度ai、扩展速度Vi及扩展时间t之间的关系为
(8)
即
(9)
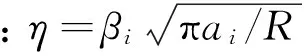
在裂缝的扩展过程中,变量有裂缝半长度ai,同时考虑外部环境的改变,外力P也可看作一个变量,其余均为常量。因此式(9)可写为
(10)
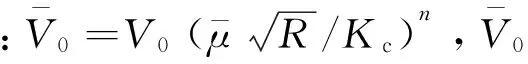
(11)
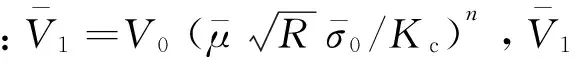
在这种情况下,对于给定粒径的某颗粒内的一条裂缝,其半长度ai仅是几何条件参数η和时间t的函数,即
(12)
10.096α4-20.778α5+20.134α6-7.507α7)]n。
(13)
裂缝长度ai是时间t的函数,即ai=ai(t),因此,α是时间t的函数,即α=α(t)。n的取值范围为[14,200]。
则式(13)可表示为如下形式:
(14)
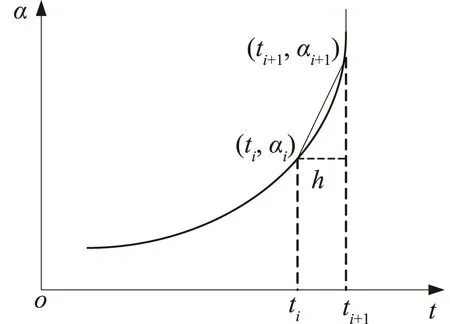
图1 斜率变化示意图Fig.1 Sketch of slope change
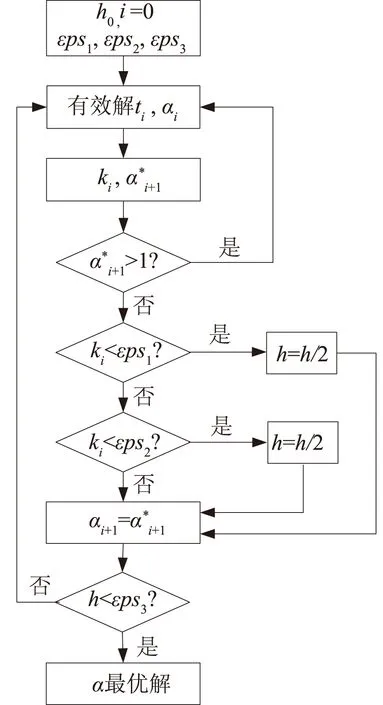
图2 计算流程Fig.2 Flow chart for calculation
裂缝扩展公式(13)是一个具有很强奇异性的常微分方程。该公式的特点是:早期的解增量缓慢,增加到某一个值后,增量迅速增加,甚至发生突变,如图1所示。因此,如何高效地选择迭代步长及寻找迭代最优解是解决该问题的关键。拟采用四阶精度的Runge-Kutta法迭代求解,并且迭代步长采用自适应步长更新,计算流程如图2所示。
现将自适应步长四阶精度Runge-Kutta法迭代说明如下。
(1) 设置算法参数:设初始步长h0=10-10,斜率下限εps1=0.1,斜率上限εps2=10,自适应步长下限εps3=10-4。
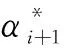
3 裂缝扩展规律及影响因素分析
3.1 颗粒体几何条件的影响
选择一组粒径为40 mm的圆球颗粒,初始裂缝半长度a0i分别为0.2,0.4,1.0,2.0,3.0,4.0 mm,初始裂缝长度与粒径的比值α0分布范围为[0.01,0.20],外荷载P=15 kN,裂缝面上的应力σ*=5.413 MPa,该应力值大于颗粒体系受到的应力(见表1)。因为颗粒体系内部力链结构引起的接触力不均匀分布,粗力链结构内的颗粒承受的接触力要大于作用于颗粒体系边界的总荷载。Nakawa等(2001)[17]指出单个砂颗粒的破碎强度是砂试样屈服强度的2~15倍。因此,认为本例选取的应力值可以代表室内单轴流变试验中堆石颗粒的真实应力水平。Charles参数n=14,V0=0.1 m/s。
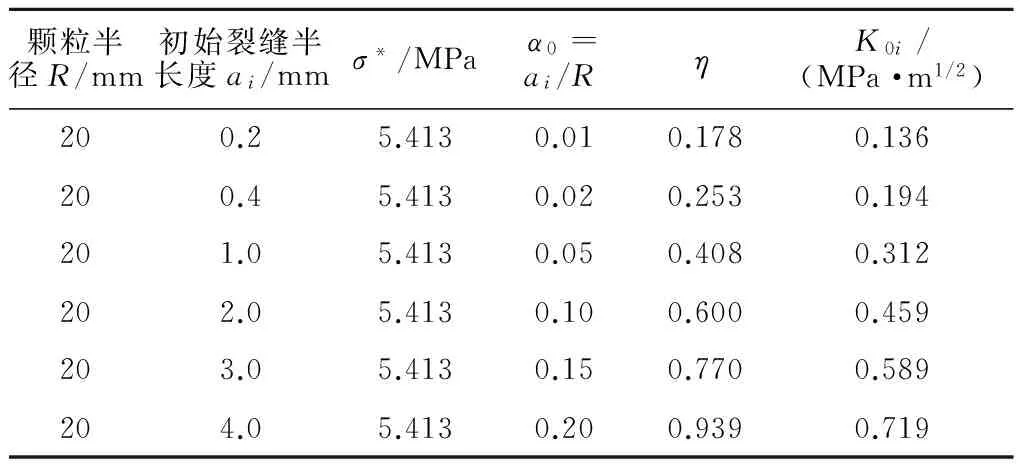
表1 亚临界裂缝扩展的计算参数(P=15 kN)
图3(a)给出了裂缝长度与粒径的比值α随时间的发展过程,可见裂缝扩展分为2个阶段:①当裂缝初始长度和颗粒粒径相比很小时,裂缝以一个相对较小且恒定的速度扩展;②裂缝扩展速度突然增大,导致颗粒在一个很短的时间内破裂。从图3(a)中还可看出,初始裂缝长度越大,裂缝扩展至颗粒破碎的时间越短。在恒定应力条件下,当初始裂缝长度在较小的范围内变化时,裂缝扩展至颗粒破碎的时间范围分布大得多。
图3(b)和图3(c)分别显出了对应不同α0工况下表征裂缝扩展几何相关性的无量纲参数η和应力强度因子随时间的发展过程(P=15 kN)。
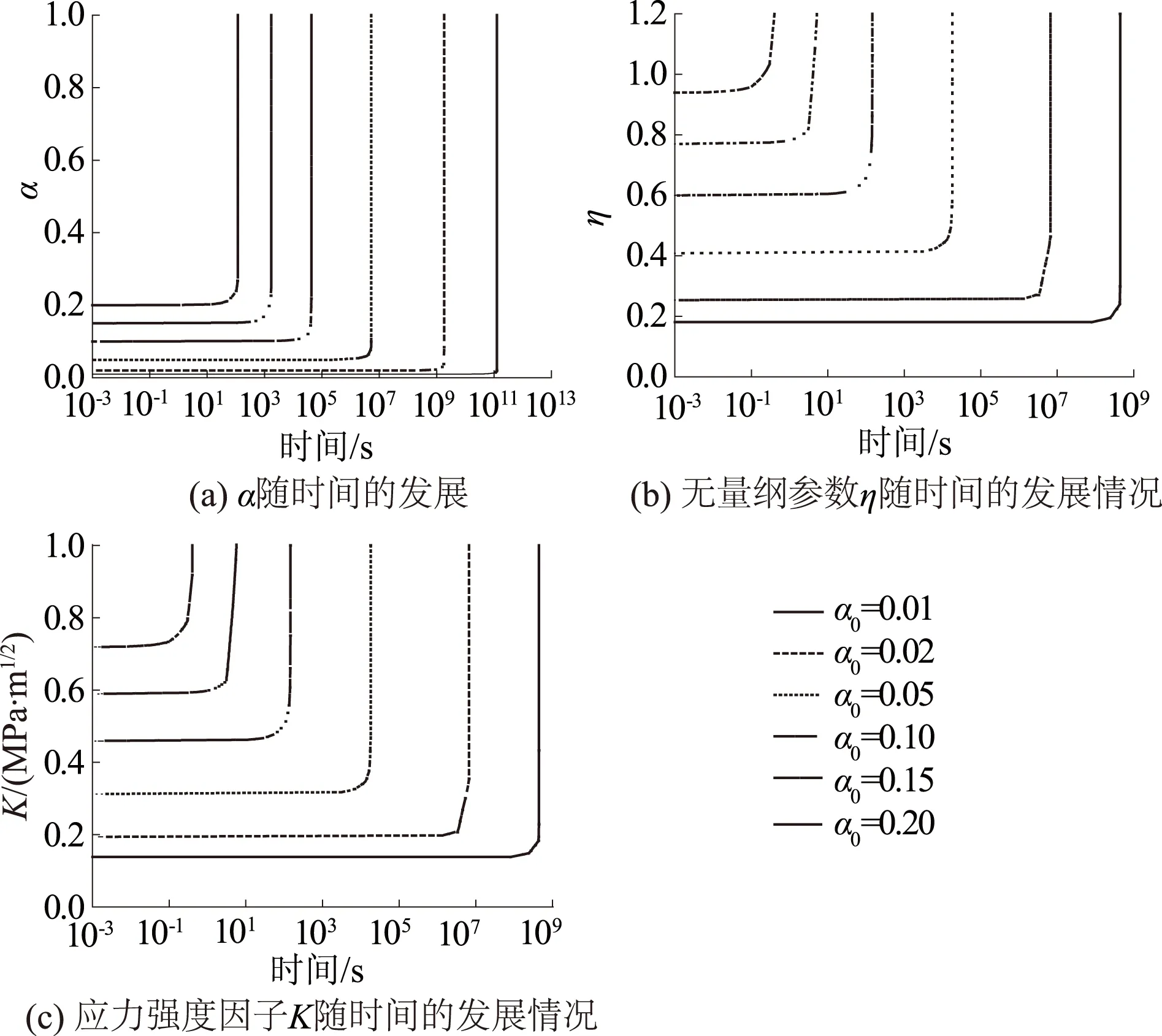
图3 颗粒体不同几何参数随时间的发展情况Fig.3 Evolution of different geometric parameters of particle vs.time
对比图3(c)显示的应力强度因子发展过程和图3(a)显示的裂缝长度扩展过程,可以看出,当外力保持恒定,在裂缝缓慢扩展的过程中,应力强度因子的变化也很缓慢,原因是图3(b)所示的表征应力强度因子几何相关性的无量纲参数η增长非常缓慢,几乎是一个常数。实际上即使应力强度因子很小时(小于起裂韧度),裂缝也在扩展,但是速度非常小;当裂缝长度比α扩展到一定程度后,应力强度因子也会进入突变期,但由于裂缝扩展速度太小,持续时间非常长,所以没有考虑的价值。同时在这漫长的扩展过程中,外部环境定然发生改变,因此一般都认为应力强度因子较小(小于起裂韧度)时,裂缝不扩展。
因此,从裂缝增长角度分析,当初始裂缝长度较小时,裂缝的扩展时间非常长,裂缝的扩展速度几乎可以忽略不计,而随着初始裂缝长度增大,裂缝的扩展速度大大增加,破碎的时间大为缩短。
3.2 应力条件与几何条件的耦合影响
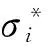
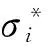
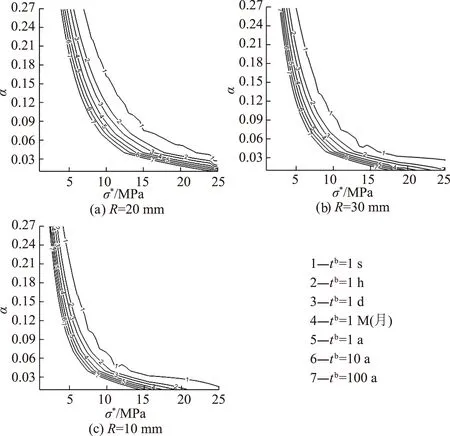
图4 裂缝面上的应力σ*和初始裂缝参数α与裂缝存活时间tb的关系Fig.4 Relationship of initial crack parameter α, the stressσ* at the surface of crack and survival time tb
3.3 湿度条件的影响
应力腐蚀是裂缝扩展的内因,应力腐蚀机制中,水的作用由相对湿度(或含水率)控制,在热力学中湿度和总吸力之间存在一一对应关系,故相对湿度对裂缝的扩展有较大影响。Atkinson(1984)[18]通过搜集和整理大量岩石材料的应力腐蚀试验数据,总结相对湿度对起韧裂度、裂缝扩展速度的影响为:相对湿度的影响主要是降低堆石的起裂韧度和断韧裂度,加速裂缝的扩展。应用Charles模型研究裂缝的应力腐蚀机制,相对湿度(含水率)通过材料参数n来反映,Alonso等(2009)[19]给出了材料参数n和相对湿度RH的关系,见图5。相对湿度越小,表明越干燥,n越大。根据图5所示的n和RH的关系,建立了不同湿度(含水率)条件下裂缝扩展规律的关系曲线,如图6所示,算例中α=[0.01,0.30],R=20 mm,σ*=5 MPa。
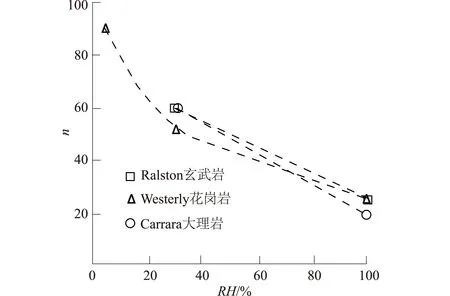
图5 材料参数n和RH的关系[19]Fig.5 Relationship between material parameter n and relative humidity RH[19]
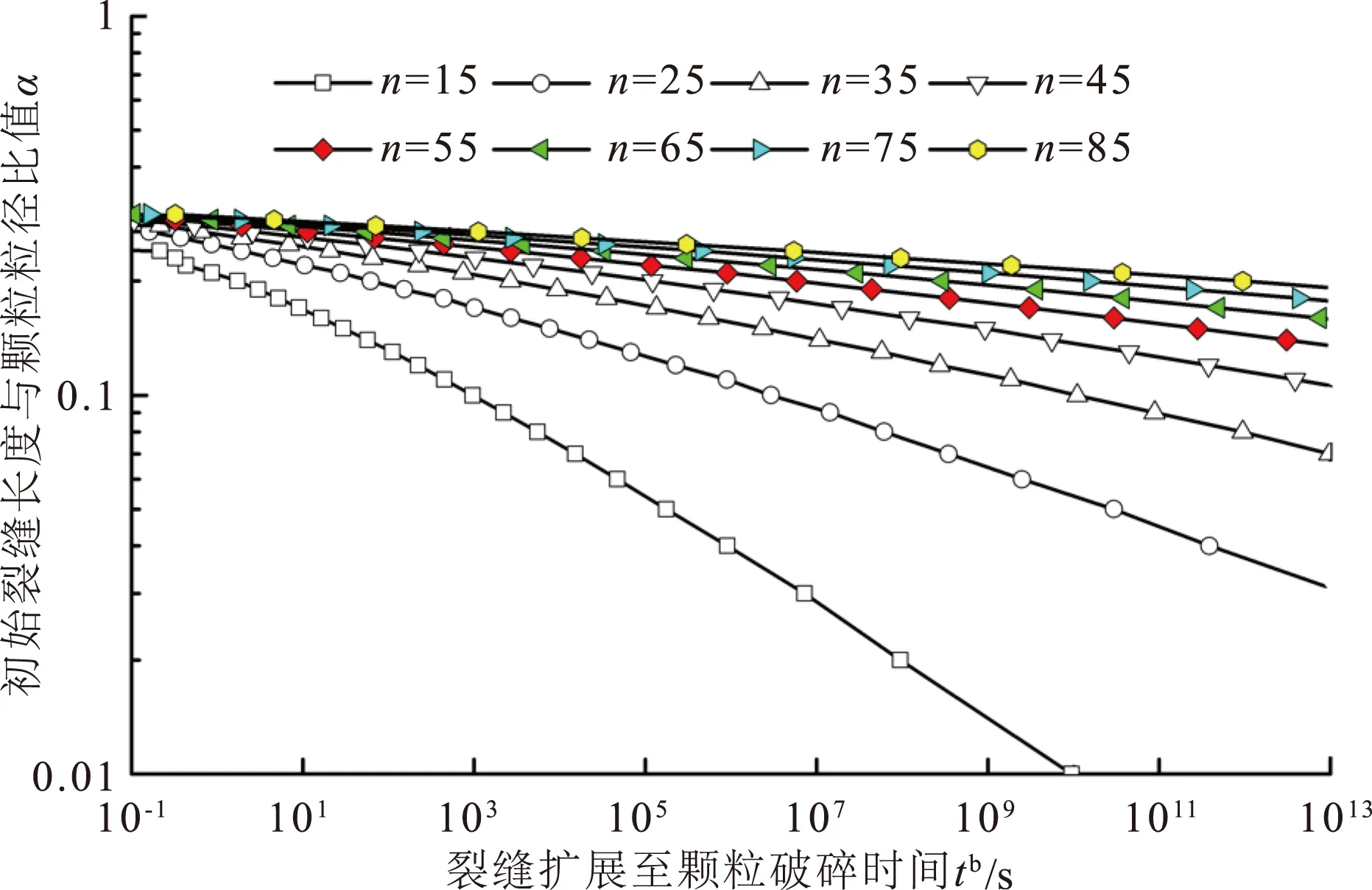
图6 不同相对湿度条件下α与tb的关系Fig.6 Relationship between survival time tb and α in the presence of different relative humidities
从图6可以看出,随着相对湿度的增大,对应某一初始α的裂缝扩展至破碎的时间tb大为缩短。以α=0.1为例,n从25减小到15后,破碎时间tb从107s数量级缩短到103s数量级。随着n的逐步增大,试样由饱和趋于干燥,起裂的初始裂缝长度相应增加;当n足够大时,只有当初始裂缝长度与颗粒粒径相比足够大,裂缝才扩展。同时,n在增大的过程中,α与tb的关系由非线性逐渐趋向于线性。另外,当初始裂缝几何尺寸α足够大时,相对湿度对裂缝扩展的影响趋于减弱,当α超过0.3后,相对湿度的影响几乎可以忽略。
由上述分析可知:相对湿度的增大可以促进微裂缝的扩展,缩短裂缝扩展至颗粒破碎的时间。当初始裂缝长度与颗粒粒径相比足够大时,相对湿度不再是影响裂缝扩展的主要影响因素。
4 结论与展望
本文根据岩石亚临界裂缝扩展理论,分析了堆石裂缝的扩展规律,探讨裂缝面上的应力、颗粒及所含裂缝的几何特征、相对湿度等因素对应力强度因子、裂缝扩展规律的影响,得到了以下一些认识:
(1) 几何、应力与湿度条件对裂缝扩展规律有一定的影响。
初始裂缝长度越大(α越大)、裂缝面上应力越大,裂缝越易处于激活的亚临界扩展状态,裂缝扩展至颗粒破碎的时间越短。
裂缝初始长度越长,越易在较小应力下扩展。换言之,α越大,裂缝对裂缝面上应力的要求越不敏感,即一个较小的应力增量就会导致破碎时间较大程度的缩短。
相对湿度增大,可降低堆石的起裂韧度和断韧裂度,促进微小裂缝的扩展,缩短裂缝扩展至颗粒破碎的时间。随着试样由饱和趋于干燥,起裂的初始裂缝长度相应增加。当初始裂缝长度与颗粒粒径相比足够大时,相对湿度不再是影响裂缝扩展的主要因素。
[1] OLDECOP L A, ALONSO E E. A Model for Rockfill Compressibility[J]. Geotechnique, 2001,51(2):127-139.
[2] OLDECOP L A, ALONSO E E. Theoretical Investigation of the Time-dependent Behaviour of Rockfill[J]. Geotechnique, 2007,57(5):423-435.
[3] 肖洪天,周维垣,杨若琼. 岩石裂纹流变扩展的细观机理分析[J]. 岩石力学与工程学报,1999,18(6):623-626.
[4] 肖洪天,周维垣,李白英. 岩石裂纹亚临界扩展机制及试验研究[J]. 工程力学,1999, (增刊):484-488.
[5] 袁海平,曹 平,周正义. 金川矿岩亚临界裂纹扩展试验研究[J]. 中南大学学报(自然科学版),2006, 37(2):381-384.
[6] 李江腾,曹 平,袁海平. 岩石亚临界裂纹扩展试验及门槛值研究[J]. 岩土工程学报,2006, 28(3):415-418.
[7] NARE Y, KANEKO K. Study of Subcritical Crack Growth in Andesite Using the Double Torsion test[J]. International Journal of Rock Mechanics and Mining Sciences, 2005,42:521-530.
[8] NARE Y, KANEKO K. Subcritical Crack Growth in Anisotropic Rock[J]. International Journal of Rock Mechanics and Mining Sciences, 43(3):437-553.
[9] WILKINS B J S. Slow Crack Growth and Delayed Failure of Granite[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1980, 17:365-369.
[10]WIEDERHORN S. M, FULLER E R,THOMSON R. Micromechanisms of Crack Growth in Ceramics and Glasses in Corrosive Environments[J]. Metal Science, 1980, 14(8): 450-458.
[11]邵 磊,迟世春,王振兴. 基于裂缝扩展的堆石料流变细观模型[J]. 岩土工程学报,2013,35(1):66-75.
[12]邵 磊,迟世春. 堆石料单轴流变试验的颗粒流模拟[J]. 岩土力学, 2013, 34(5):1487-1500.[13]BROEK D. Elementary Engineering Fracture Mechanics[M]. Dordrecht: Martinus Nijhoff,1986.[14]TADA H, PARIS P,IRWIN G R. The Stress Analysis of Cracks Handbook[M]. 2nd ed. St Louis, MO: Paris Productions, 1985.
[15]曲 嘉. 钢纤维混凝土劈拉强度的实验研究[D]. 哈尔滨:哈尔滨工程大学,2010.
[16]CHARLES R J. Static Fatigue of Glass[J]. Journal of Applied Physics, 1958,29(11): 1549-1560.
[17]NAKAGAWA S,MYER L R. Mechanical and Acoustic Properties of Weakly Cemented Granular Rocks[C]∥ELSWORTH D, TINUCCI J P, HEASLEY K A. Proceedings of 38th U.S. Symposium on Rock Mechanics: Rock Mechanics in the National Interest. (Vol.1), Washington D.C.,USA, July 7-10,2001:3-10.
[18]ATKINSON B K. Subcritical Crack Growth in Geological Materials[J]. Journal of Geophysical Research, 1984,:4077-4114.
[19]ALONSO E E , OLDECOP L. Long Term Behaviour and Size Effects of Coarse Granular Media[M]. Mechanics of Natural Solids, 2009: 255-281.
(编辑:黄 玲)
Subcritical Crack Expansion of Rockfill Particleand Its Influencing Factors
SHAO Lei1,YU Ting1,CHI Shi-chun2
(1.PowerChina Chengdu Engineering Corporation Limited, Chengdu 610072, China; 2.Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China)
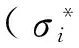
rockfill particle;sub-critical model of crack expansion; particle breakage;stress intensity factor; relative humidity
2014-08-02;
2014-11-11
国家重点基础研究发展计划(973)项目(2013CB036400);国家自然科学基金项目(50879007,50979014,51179024)
邵 磊(1983-),男,河北张家口人,工程师,博士,主要从事筑坝堆石料流变及高土石坝抗震研究方面的工作,(电话)028-87392840(电子信箱)sl-fly@163.com。
10.11988/ckyyb.20140636
2016,33(01):115-120
TU345
A
1001-5485(2016)01-0115-06
