基于AR（1）模型的纯保费的Monte Carlo模拟研究

关清元，洪梦莹

（武夷学院数学与计算机学院，福建武夷山354300）

基于AR（1）模型的纯保费的Monte Carlo模拟研究

关清元，洪梦莹

（武夷学院数学与计算机学院，福建武夷山354300）

把随机利率，转化成年利率，然后用AR（1）模型进行拟合，并利用SPSS软件对拟合做出检验。经检验拟合效果比较好，模型可用。以当前热销的前海人寿保险有限公司的万能保险为实证分析，用Monte Carlo模拟的方法，借助MATLAB软件求出了趸缴纯保费，并预测了在3σ原则下的纯保费区间。

年平均加权利率；AR（1）模型；SPSS软件；Monte Carlo模拟；3σ原则

在国内，运用MonteCarlo技术对纯保费所做的研究不多。1997年蒋庆荣[7]在《随机利率下的终身寿险》中得到了终身寿险的纯保费的计算公式；2001年，良艳怀,玛恩民[8]在《随机利率下综合人寿保险模型》中，考虑了随机过程函数，给出了综合人寿保险模型；2003年王丽艳,柳扬[9]在《随机利率下的准备金与寿险风险分析》中采用了Bayes方法，得到了死亡率的经验分布；2005年东明[10]在《申汇养老保险中隐性债务的双随机模型》中采用了Wiener Process model对养老保险隐性债务进行建模。

以上这些论文没有考虑用AR过程来模拟,运用适当的方法证明了用AR过程来建模，在现实生活中是可行的，然后采用Monte Carlo模拟的方法得到了特定条件下纯保费的分布区间。在实证分析中，运用Matlab软件并结合Spss软件，首次对万能保险的趸缴纯保费，进行了大量快速的模拟，对提高万能保险趸缴纯保费的精度进行了新的尝试。

1 随机利率下的AR(1)模型

1.1 数据处理

中国人民银行官方网站：一年期定期存款利率的调整如表1所示：

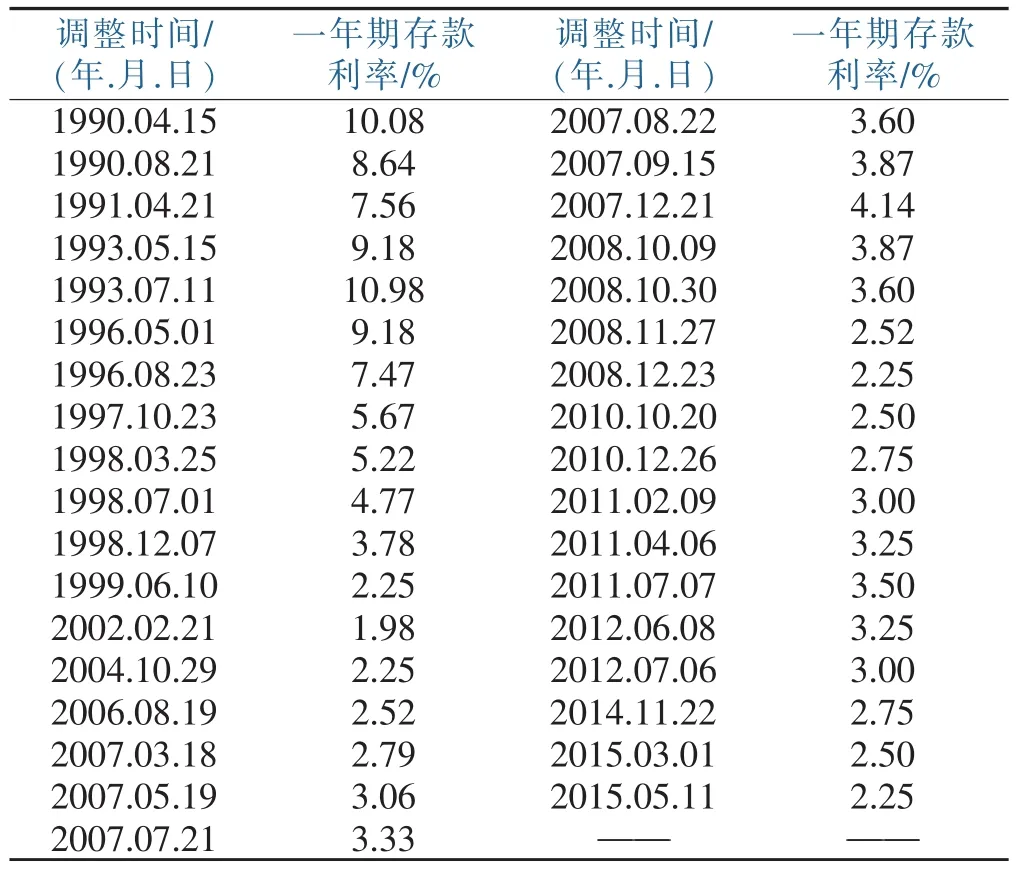
表1 存款利率

由于每次调整，都会相应的维持一个时间区间，即可以把这些时间点看成是一个连续的时点序列。所以下面采用按照时间段加权的方法[11]，将其转化为一个整数年的利率，公式为,其中表示当年的平均利率水平，ik表示当年第k个利率水平，fk则表示第k个利率水平所维持的天数。由此计算可得各年的年平均利率如表2所示：

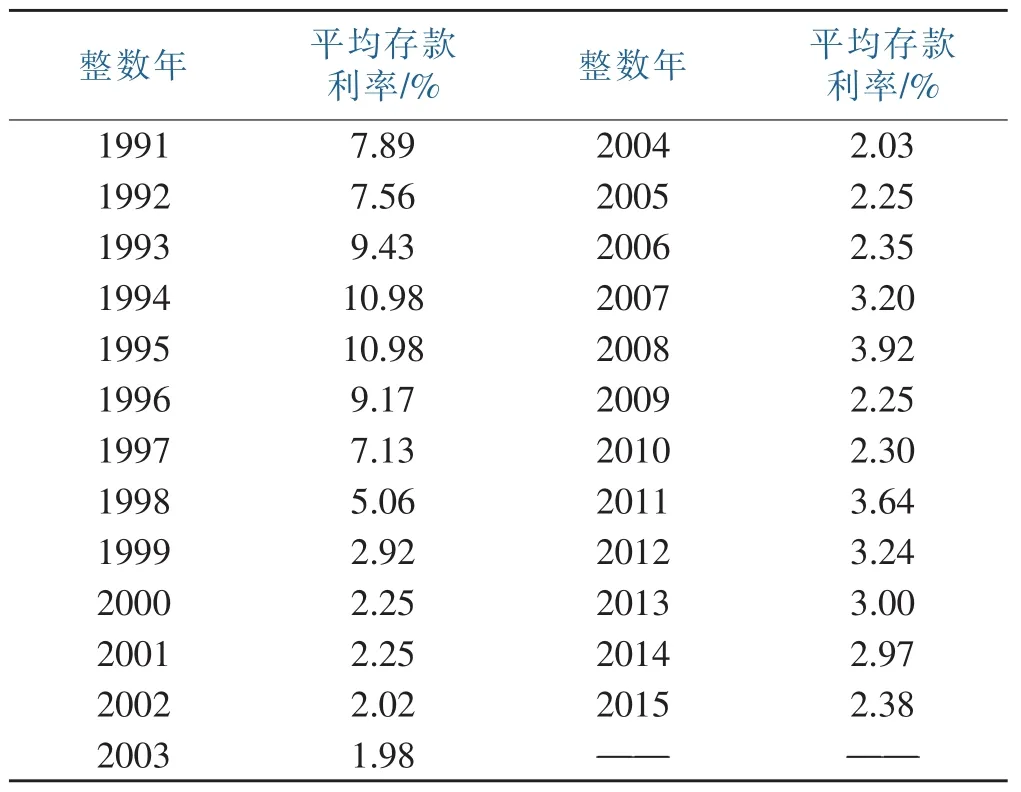
表2 年平均利率

1.2 利率模型的拟合

根据设定的情景条件，对5个影响因素每隔0.5 h采集一次样本数据，采用调查问卷法得到影响因素的定性判定数据。各因素风险状态划分为强+(A)，强(B)，中等(C)，弱(D)，弱-(E)5个状态。

由于AR（1）模型是回归模型的范畴，用SPSS软件做散点图如下：

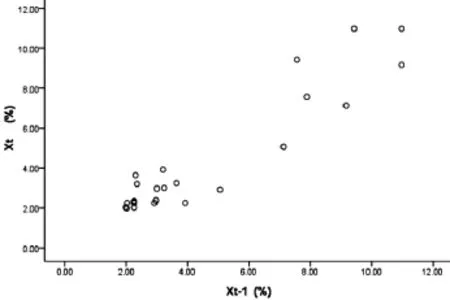
图1 前一年利率Xt-1与后一年利率Xt的关系散点图

从图1可以看出：Xt-1与Xt在较大程度上呈线性关系。所以初步判断对其用AR（1）模型来拟合是可行的。

下面用SPSS软件对Xt-1与Xt的数量关系来进一步地求解，从而求出AR（1）模型的参数。以下为SPSS的分析结果表：

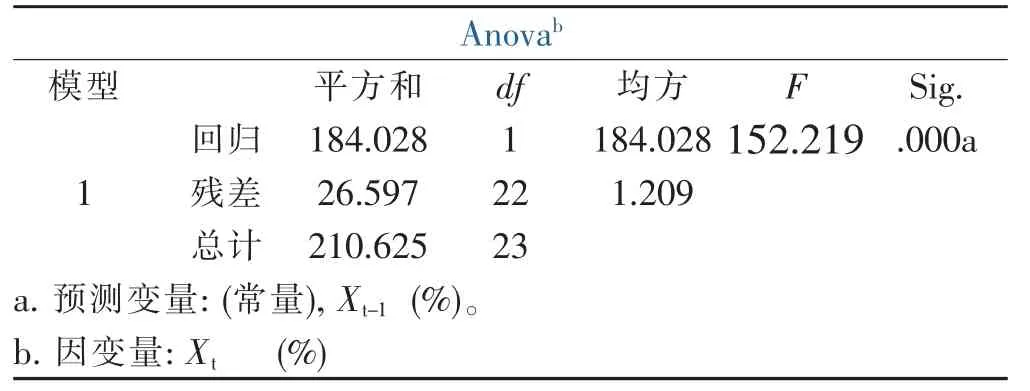
表3 回归变异图

由表3可以看出，Regression为184.028，Residual Total为26.597，对应的F统计量的值为152.219，且152.219fF0.05（1，22）=4.30,又因为显著性水平sig.= 0.000≺0.05所以可以认为所建立的回归方程有效。

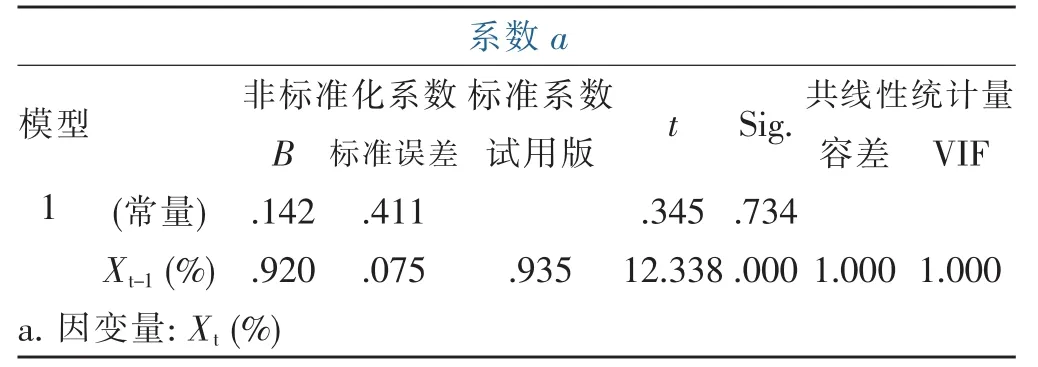
表4 回归系数表

由表4可以看出，非标准化的Regression coefficient的估计值为0.920，标准Error为0.075，标准化的Regression coefficient为0.935，回归系数显著性检验的t统计量的值为且12.338，且12.338≻t0.025（22）= 2.074,对应的显著性水平sig.=0.000≺0.05,故可以认为方程是显著的。

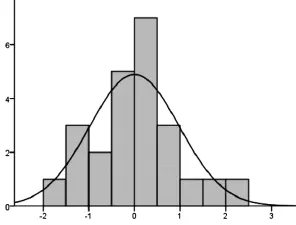
图2 标准化残差直方图

图2，反映了残差的分布情况，根据图形来看，残差项基本符合标准正态分布。

综上所述，可得利率模型为：

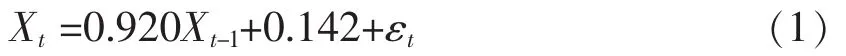
2 前海人寿万能保险的montecarlo模拟实证

考虑到现在大多数人倾向于购买万能保险，且据一些保险公司透露，在销售的所有保险产品中，万能险的比例已经达到了30%～40%。万能保险既能够提供人身保障，又能够作为投资。

以前海人寿保险股份有限公司销售的万能险为例，由于万能险的保险额度设计有多种，本文特根据《万能保险精算规定》做出如下假设：提供2.5%的结算收益率保底。

某男50岁投保前海人寿万能保险，保险期间是10年，该男在保险期内身故，在年末公司支付1万元的身故保险金；如生存至期满，同样可获得1万元的满期保险金。试分析该男的趸缴纯保费[12]。以当前2.38%的利率水平为基础，对未来10a的利率情形进行随机模拟，得出趸缴纯保费的可能值，对上述过程进行6000次MonteCarlo模拟，得出结果。

根据万能保险的趸缴纯保费公式：

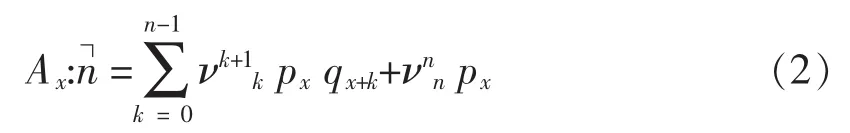
而在每年是变化利率的情况下，此式演变为:

根据中国人寿保险业男性经验生命表（2000～2003）可得：

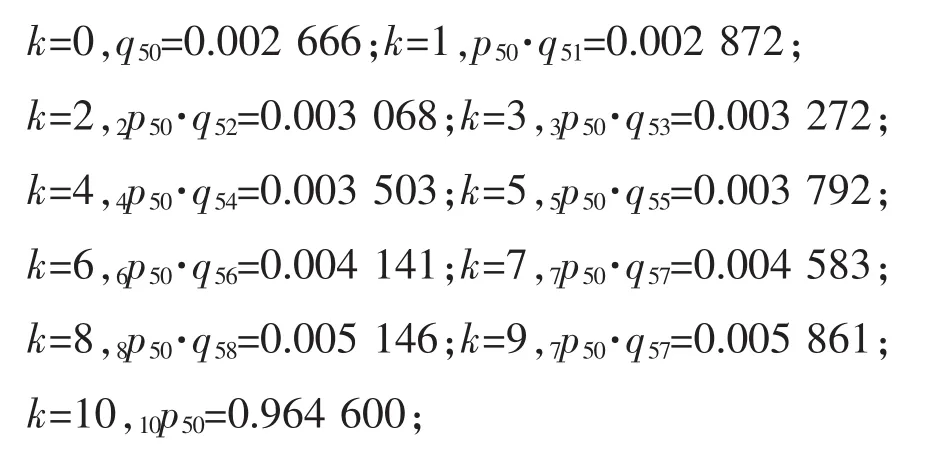
前海人寿10年期万能保险趸缴纯保费Monte Carlo仿真的MATLAB代码为:

forj=1:6000;

fori=1:9;

x(1)=2.38;

x(i+1)=x(i)*0.920+0.142+randn(1,1);

end;

y(j)=0.002666/(1+x(1)/100)+0.002872/(1+x(1)/100)/(1+x (2)/100)+0.003068/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/ 100)+0.003272/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/ (1+x(4)/100)+0.003503/(1+x(1)/100)/(1+x(2)/100)/(1+x(3) /100)/(1+x(4)/100)/(1+x(5)/100)+0.003792/(1+x(1)/100)/ (1+x(2)/100)/(1+x(3)/100)/(1+x(4)/100)/(1+x(5)/100)/(1+x (6)/100)+0.004141/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/ 100)/(1+x(4)/100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100) +0.004583/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/(1+x (4)/100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100)/(1+x(8)/ 100)+0.005146/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/ (1+x(4)/100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100)/(1+x (8)/100)/(1+x(9)/100)+0.005861/(1+x(1)/100)/(1+x(2)/ 100)/(1+x(3)/100)/(1+x(4)/100)/(1+x(5)/100)/(1+x(6)/100)/ (1+x(7)/100)/(1+x(8)/100)/(1+x(9)/100)/(1+x(10)/100)+ 0.9646/(1+x(1)/100)/(1+x(2)/100)/(1+x(3)/100)/(1+x(4)/ 100)/(1+x(5)/100)/(1+x(6)/100)/(1+x(7)/100)/(1+x(8)/100)/ (1+x(9)/100)/(1+x(10)/100)

end;

y

mean(y)

std(y)

通过此代码，可以得到在Monte Carlo模拟下的平均趸缴纯保费mean（y）=8162元，标准差std(y)= 1070,则根据正态分布的3σ原则，可得趸缴纯保费以68.26%的概率落在区间[7092,9232]上,以99.74%的概率落在区间[4952,11372]上。又根据此险种的保底收益率，可得实际趸缴纯保费以68.26%的概率落在区间[5540,7212]上,以99.74%的概率落在区间[3 868,8883]上。

3 小结

根据每个时间点的利率数据进行时间加权平均、AR(1)模型的构建以及用spss去做拟合的检验。最后用Monte Carlo模拟的方法对前海人寿保险公司一款热销的万能保险产品进行趸缴纯保费的实证分析，此测算是借助MATLAB软件平台所做。对人寿保险公司的其他的一些产品，可以类似的进行拟合化的控制预测，对保险公司定价风险的控制提供了新的思路，对于保险公司产品设计、运营和监控具有一定的借鉴意义。

[1]Milevsky M A.The presnt value of a stochastic perpetuity and the gamma distribution[J].Insurance:Mathematics and Economics,1997(20):243-250.

[2]Milevsky M A.Martingales scale functions and stochastic life annuities a not[J].Insurance:Mathematics and Economics, 1999(24):149-154.

[3]Kaas R,Dhaene J,Goovaerts M J.Upper and lower bounds for sums of variables[J].Insurance:Mathematics and Economics, 2007(27):151-168.

[4]De A,Goovaerts M J,Dhaene J,et al.Bounds for present value funcions with stochastic interest rates and stochastic volatility [J].Insurance:Mathernatics and Econornics,2002(31):87-110.

[5]Perry D，Stadje W·Function space intenration for annuities [J].Insurance:Mathematics and Economics,2001(29):73-82.

[6]Perry D,Stadje W,Yosef R.Annuities with controlled random interest[J].Insurance:Mathematics and Economics,2003(32): 245-253.

[7]蒋庆荣.随机利率下的终身寿险[J].杭州大学学报（自然科学版）,1997(2):8-14.

[8]良艳怀,玛恩民.随机利率下综合人寿保险模型[J].大连理工大学学报,2001(5):29-31.

[9]王丽燕.随机利率下的准备金与寿险风险分析[J].大连大学学报,2003(4):17-35.

[10]东明,郭亚军,杨怀东.社会养老保险中隐性债务的双随机模型[J].系统工程学报,2005(6):570-577,643.

[11]贾怀勤.应用统计[M].北京：对外经贸教育出版社,1994: 45-54.

[12]杨静平.寿险精算基础[M].北京：北京大学出版社，2010.

（责任编辑：夏婷婷）

Simulation of Pure Premium of Carlo Monte Based on AR(1)M ode

GUAN Qingyuan，HONG Mengyin
(School of Mathematics and Computer Science,Wuyi University,Wuyishan,Fujian 354300)

In this paper,it changes random interest rate into annual interest rate.Then it uses the AR(1)model to fit the rate.And it tests the fitting by using the SPSS Software model.lt calculates the net single premium by using matlab software and it predicts the pure premium interval of the principle of“three”,taking for example universal life insurance,hotly sold by sea life insurance company, by using the method of Monte Carlo simulation.

average weighted interest rate;AR(1)model;SPSS software;Monte Carlo simulation;threeσprinciple

F224；F842

A

1674－2109(2016)09－0073－04

2016-03-24

武夷学院科技类项目(XD201405)；国家级大学生创新训练项目(201410397002)。

关清元(1981-)，男，汉族，讲师，主要从事计算数学、保险精算方向研究。