3D MIMO信道建模与仿真验证

2016-12-01赵雄文张梦媛张蕊李树林乐科

电信科学 2016年8期

赵雄文，张梦媛，张蕊，李树，林乐科

（1.华北电力大学，北京 102206；2.中国电波传播研究所电波环境特性及模化技术国防科技重点实验室，山东青岛266107；3.东南大学移动通信国家重点实验室，江苏南京 210096）

3D MIMO信道建模与仿真验证

赵雄文1，2，3，张梦媛1，张蕊2，李树1，林乐科2

现有的多输入多输出（MIMO）信道仿真模型主要基于二维（2D）平面，不能反映实际的三维（3D）电波传播环境。在WINNER 2D模型的基础上研究建立3D MIMO信道仿真平台。加入空间垂直维后，天线方向图需要从2D扩展至3D，并对3D天线阵列构成的MIMO系统进行建模。利用实验数据对城市微小区场景进行仿真验证，可以看出三维MIMO信道参数仿真与实验结果符合较好。3D MIMO信道间的相关性要比2D大，但3D MIMO的信道容量相比2D会有比较大的提升。

3D MIMO；信道仿真；信道参数；信道相关性；信道容量

1 引言

多输入多输出（multi-input multi-output，MIMO）信道模型在第四代（4G）和第五代（5G）移动通信链路和系统级仿真中都有重要的应用价值。3GPP SCM、WINNER和COST2100 信道仿真模型［1-3］已广泛应用于第三代（3G）移动通信和LTE信道仿真中，但它们都是二维（two dimensional，2D）模型，没有考虑电波和天线在垂直面内的影响。随着LTE-Advanced（以下简称LTE-A）和 5G的发展，三维（three dimensional，3D）MIMO信道建模和仿真成为目前国内外研究的热点［4-6］，初步研究结果表明，将MIMO信道模型从二维扩展至三维是非常必要的。

目前国际标准化组织3GPP TSG-RAN-WG1提出了基于WINNER的 3D MIMO模型［4］，主要通过空间电波垂直面的引入进行模型扩展工作，对坐标系、天线方向图、二维天线阵列、新的路径损耗模型、小尺度衰落模型等内容都做了相应修改，提供了三维城市微小区（3D urban micro cell，3D-UMi）和三维城市宏小区（3D urban macro cell，3D-UMa）场景完整的特征参数表，但目前还未提供信道软件仿真平台。参考文献［6］介绍了WINNER+信道模型，同时也介绍了将WINNER信道模型由二维扩展到三维的思路。国内对3D MIMO信道的建模和仿真也做了相关的研究，参考文献［7］对3D MIMO模型垂直面角度的分布和电波在三维空间的传播特性进行了研究；参考文献［8］对3D MIMO的关键技术和原理进行了综述性介绍。在信道测试方面，参考文献［9］针对 UMi、UMa以及室外到室内（outdoor-to-indoor，O2I）场景进行了3D MIMO测量，分析了电波到达角和离开角在水平面和垂直面的统计特性。

本文基于参考文献［4］建立了3D MIMO信道仿真平台，将坐标系、天线方向图、终端和基站（base station，BS）高度、散射体垂直角度等内容扩展至三维空间，通过仿真得到3D MIMO信道冲激响应矩阵，开展信道参数的提取工作。基于WINNER项目中典型场景下大量的三维实测数据，对所建3D MIMO仿真平台进行验证。最后对2D和3D信道模型的空间相关性和信道容量进行了对比。

2 3D MIMO信道建模

2.1 天线阵列

3D MIMO天线阵列模型支持任意结构的天线阵列，在系统布局中，定义两个坐标系：全局坐标系（global coordinate system，GCS）和局部坐标系（local coordinate system，LCS），分别用于全局拓扑和天线阵列的定位。在3D模型中，GCS和LCS须扩展至三维，引入z轴与高度角，并重新定义坐标转换矩阵，GCS和LCS转换如图1所示。

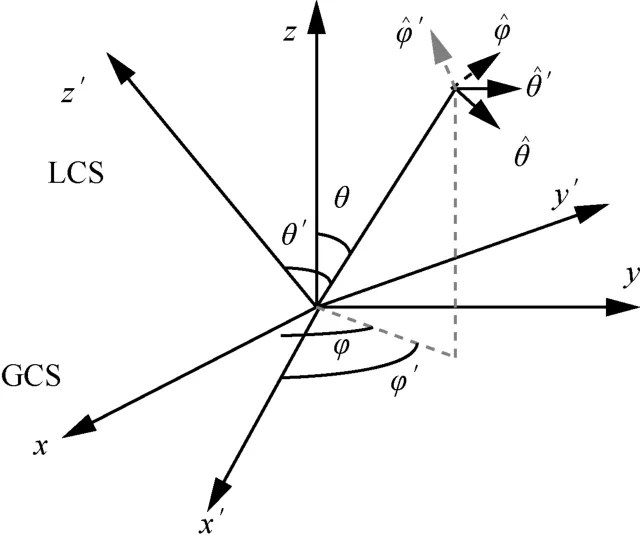
图1 全局坐标系与局部坐标系转换示意

从 GCS（x，y，z）到 LCS（x＇，y＇，z＇）的旋转可定义旋转矢量rot=［α，β，γ］，其中，α、β、γ 分别表示 ACS 坐标系相对于 LCS坐标系的x、y、z轴的旋转弧度，则转换矩阵为：

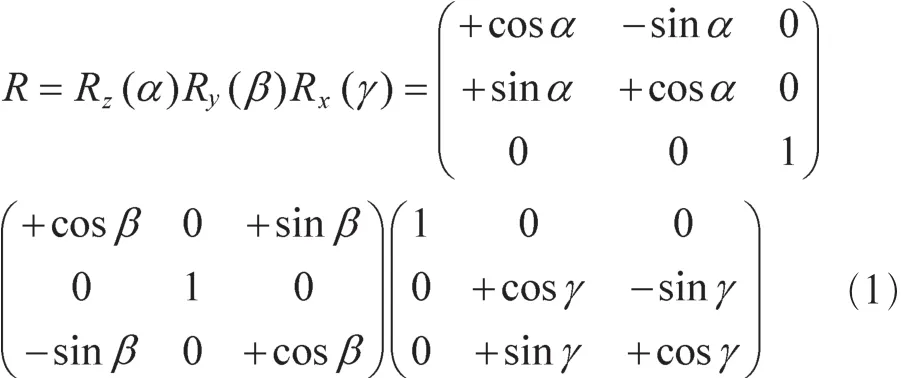
天线具有在一定方向辐射电磁波的能力，使用天线方向图来表示。为便于分析，本文信道建模中考虑的天线阵是均匀线性阵列（uniform linear array，ULA）和均匀圆形阵列（uniform circular array，UCA）。对于每个天线单元，天线方向图包含了天线的极化方向和大小，需扩展至三维并用F（θ，φ）表示：

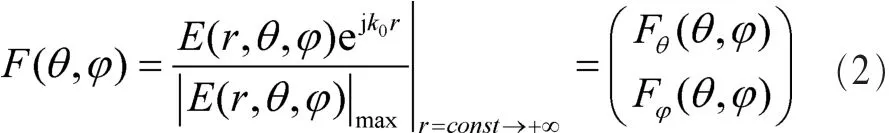
其中，E（r，θ，φ）为电场矢量，（r，θ，φ）代表电场矢量在球面坐标系中的位置，k0为波数。

假设全局坐标系中的天线仰角和方位角方向图分别为 Fθ（θ，φ）和 Fφ（θ，φ），局部坐标系中的天线仰角和方位角方向图分别为 Fθ＇（θ＇，φ＇）和 Fφ＇（θ＇，φ＇），则它们之间的关系定义如下：

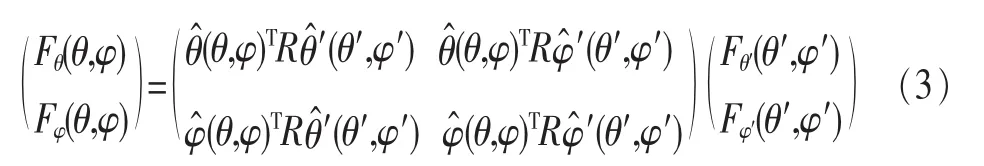
其中，^θ和^φ为全局坐标系中的单位矢量，^θ＇和^φ＇为局部坐标系中的单位矢量。

2.2 信道系数

在得到天线阵列响应后，需要生成3D MIMO信道脉冲响应，3D MIMO信道系数建模仍采用3GPP仿真方法，即基于几何基础的随机信道仿真方法［1］，利用式（4）生成信道系数：

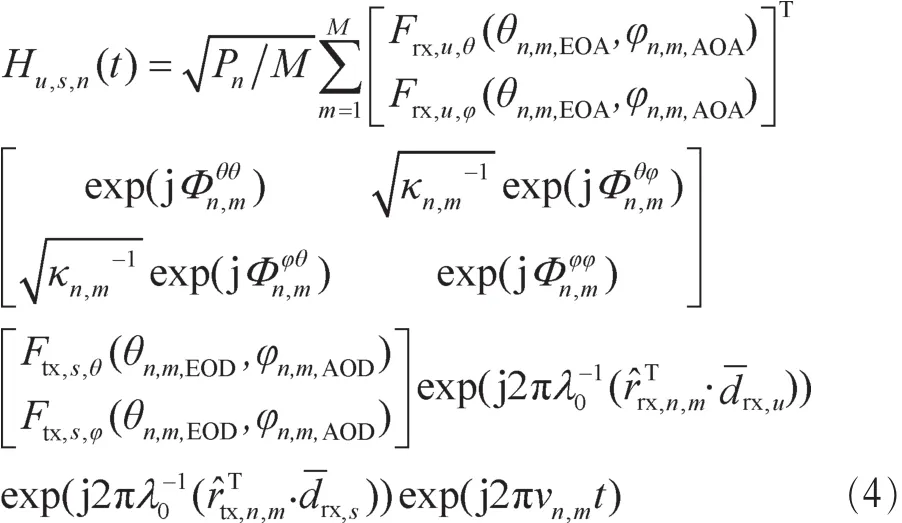
其中，s为发射阵列天线单元，u为接收阵列天线单元。M是第n个簇的子径数目，Pn为第n个簇的功率，为簇n的第m条子径的交叉极化功率比，为极化天线的初始相位。Frx，u，θ和 Frx，u，φ是接收天线单元 u 的垂直与水平天线方向图，Ftx，s，θ和 Ftx，s，φ是发射天线单元 s 的垂直与水平天线方向图。θn，m，EOA、θn，m，EOD、φn，m，AOA和 φn，m，AOD分别为簇 n的第m条子径的垂直到达角、垂直离开角、水平到达角和水平离开角。r^rx，n，m和r^tx，n，m分别是是收发端附近簇 n 的第 m条子径在球坐标上的单位向量，drx，u和dtx，s分别是接收阵列天线单元u和发射阵列天线单元s的位置矢量。利用式（4）开展3D MIMO仿真，主要步骤如下所示。

步骤1 选择场景和全局坐标系，并定义垂直角θ、方位角 φ，给出基站和移动台（mobile station，MS）的位置、天线阵列参数；根据实际场景测试得到的信道参数，确定基站和移动端的水平到达角和离开角、垂直到达角和离开角；最后给出移动端相对于全局坐标系的移动速度和移动方向以及系统的中心频率。

步骤2 基于实测信道参数分布和路径损耗模型，在视距（line of sight，LOS）和非视距（non line of sight，NLOS）传播条件下，计算基站到移动端链路的路径损耗，随机产生时延扩展、角度扩展、莱斯因子K和阴影衰落等大尺度参数。

步骤3 基于簇分布产生第n个簇功率Pn，并产生该簇中不同多径分量的多径功率、额外时延和相位；通过子径的随机配对生成交叉极化功率比（cross polarization power ratio，XPR）。

步骤4 随机初始化相位生成信道系数，为每个多径以及不同极化组合生成随机初始化相位，然后生成发射端到接收端所有簇的信道系数。

3 3D MIMO信道仿真模型的实验验证

3.1 信道测量和环境

本文选取UMi场景，对3D MIMO信道模型进行仿真验证。测试中心频率为5.25 GHz，带宽为100 MHz，信道测量参数设置见表 1［2］。

表1 系统测试参数

3.2 大尺度参数的验证

大尺度参数可以有效地描述无线信道的特征，本文对3D MIMO信道的仿真研究基于以下大尺度参数：均方根时延扩展（delay spread，DS）、水平离开角均方根角度扩展（azimuth spread of departure，ASD）、水平到达角均方根角度扩展（azimuth spread of arrival，ASA）、垂直离开角均方根角度扩展（elevation spread of departure，ESD）、垂直到达角均方根角度扩展（elevation spread of arrival，ESA）和莱斯因子K。选取LOS场景和NLOS场景下信道测量获取的参数作为输入参数进行仿真，仿真参数设置见表 2［2，6］。

表2 系统仿真参数设置（LOS／NLOS）

将表2的参数输入仿真平台，并设置UMi环境和天线参数等，生成相关大尺度参数和信道系数，将仿真生成的参数值与WINNER 3D实验测量值进行比较。图2为LOS和NLOS场景下的均方根时延扩展的累积概率分布函数（cumulative distribution function，CDF）的比较，可以看出，本文仿真与实验结果符合较好。图3（a）和图3（b）分别是基站和移动台ASD和ASA仿真和实验结果的比较。图4（a）和图 4（b）分别是基站和移动台 ESD和 ESA仿真和实验结果的比较。结果表明，本文仿真值同测量值比较接近。在UMi场景下，移动站的水平角和垂直角扩展比基站的大，在NLOS情形下角度扩展比LOS时大。

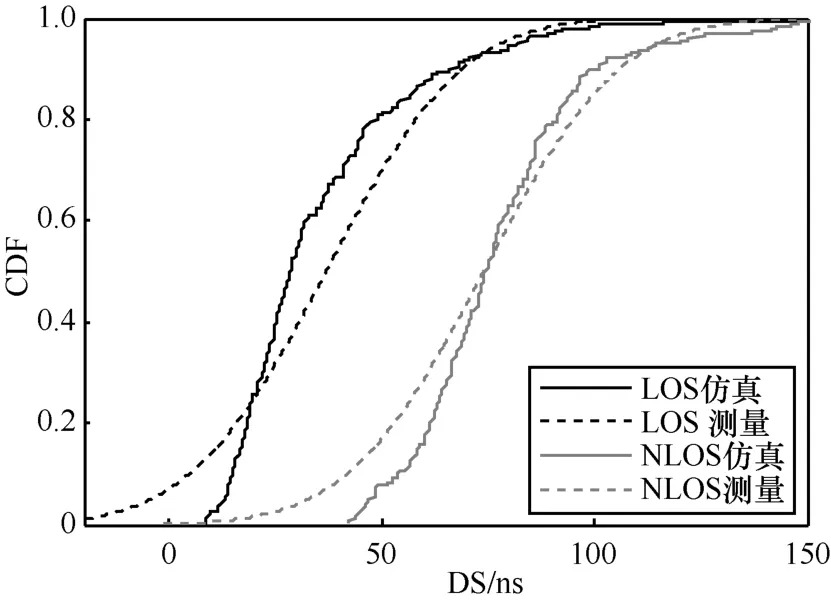
图2 均方根时延扩展比较

本文还仿真了阴影衰落（shadow fading，SF）和莱斯因子K，其结果也与实验一致。表3是大尺度ASD、ASA、ESD、ESA、SF、DS和莱斯因子K间相关性仿真与实验结果的比较。可以看出本文仿真与实验结果的一致性。

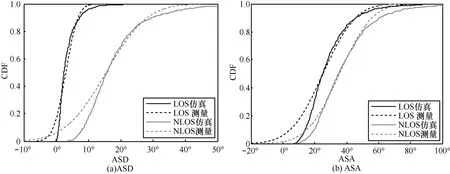
图3 BS和MS水平面均方根角度扩展比较

图4 BS和MS垂直面均方根角度扩展比较

3GPP和北京邮电大学等都在典型场景下进行了三维信道测量［4，5，7，9］，参考文献［5］得到 3D MIMO 的一些仿真结果，参考文献［7，9］主要研究了垂直维度的均方根角度扩展等参数，但这些参考文献中没有给出3D MIMO信道仿真需要的天线增益、大尺度输入参数及它们的相关性。因此本文主要基于参考文献［5，9］中的UMi场景下 3D MIMO仿真输入参数作为本文3D仿真平台的输入，生成信道冲激响应矩阵，根据仿真信道矩阵提取信道大尺度参数，研究它们的统计特性和相关性，再与参考文献［5，9］中的测量值进行比较。表4给出本文仿真输入的ESD与ESA与参考文献［5，9］测试结果的比较，可以看出本文仿真输入结果与参考文献［5］的结果非常接近，但与参考文献［9］有较大区别。主要原因是参考文献［5］和本文所采用的实验数据都基于欧洲WINNER项目典型城市UMi场景，而参考文献［9］基于国内城市UMi场景，不同的UMi场景会导致大尺度参数统计规律的变化。

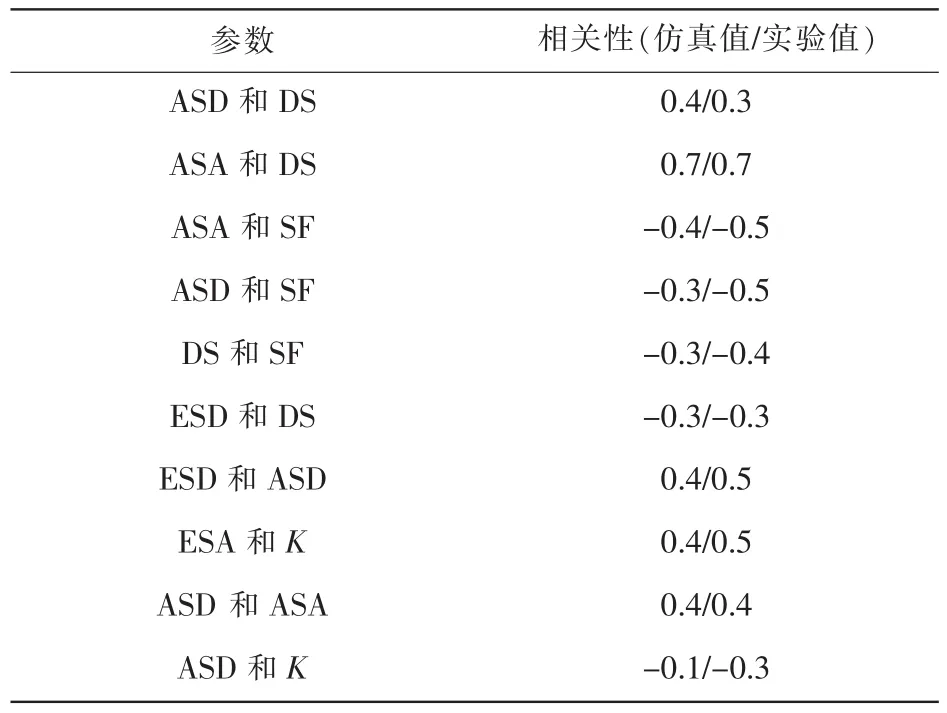
表3 参数间的相关性

4 3D MIMO与2D MIMO信道仿真比较

第3节中开展了大尺度信道参数3D MIMO仿真和实验结果的比较研究，那么3D MIMO和2D MIMO的信道参数和函数到底有多大区别，本节主要开展这方面的研究。仿真的环境仍然为UMi场景，载频为5.25 GHz，带宽为100 MHz，收发端天线类型和天线数目可自行配置。通过在该场景下对3D MIMO与2D MIMO的均方根时延等大尺度参数、MIMO空间相关性和信道容量进行比较分析，仿真中2D MIMO与3D MIMO的仿真参数在水平方向上相同，3D MIMO在垂直维上需要输入均方根角度扩展等参数。

4.1 均方根时延扩展

图5给出了UMi场景下3D与2D的均方根时延扩展仿真结果比较。可以看出，2D和3D均方根时延扩展区别不大，3D比2D略大，视距场景下结果几乎重合，非视距场景下两者差别最大有5 ns。进一步研究表明，3D MIMO和2D MIMO仿真结果对阴影衰落和莱斯因子影响也不大。

图5 2D MIMO与3D MIMO均方根时延扩展比较

4.2 信道空间相关性

对于三维均匀线性阵列和均匀圆形阵列天线，阵元m和n之间的空间衰落相关函数可表示为［10］：

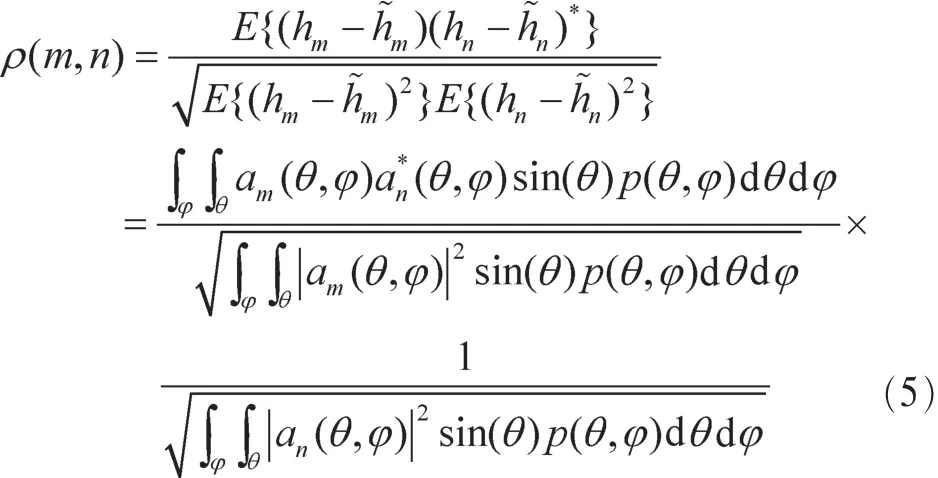
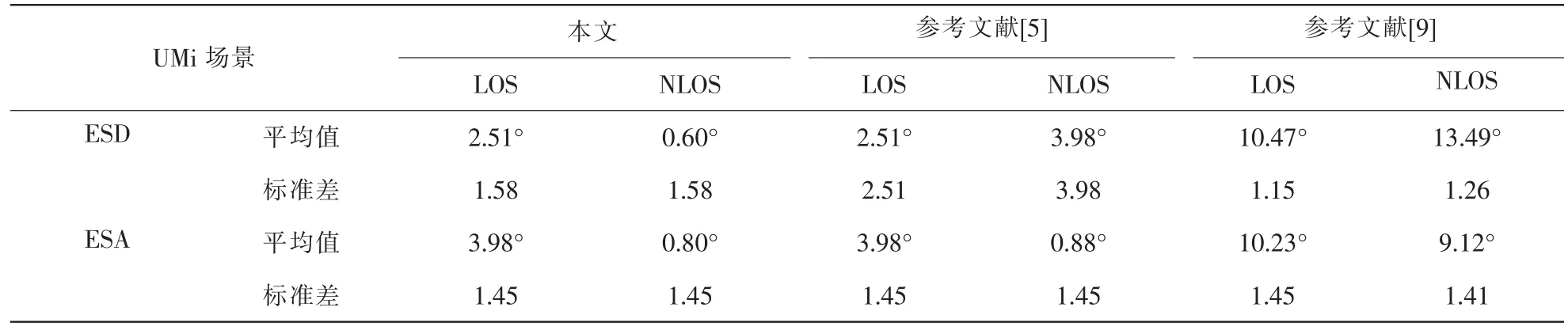
表4 UMi场景下的垂直面均方根角度扩展比较

其中，E［·］表示期望，（·）*表示共轭复数，hm和 hn分别表示m和n个天线的信道脉冲响应的平均值。p（θ，φ）是多径分量到达角的概率密度函数，假设水平到达角和垂直到达角相互独立且服从均匀分布，则 p（θ，φ）可分解为 p（θ）p（φ）。水平到达角 φ 在［φ0-Δφ，φ0+Δφ］间均匀分布，其中，φ0、Δφ分别是水平到达角的平均值和角度扩展；垂直到达角θ在［θ0-Δθ，θ0+Δθ］间均匀分布，其中，θ0、Δθ分别是垂直到达角的平均值和角度扩展，am（θ，φ）为第m个到达天线阵列的空间导向矢量，ULA的空间导向矢量为：

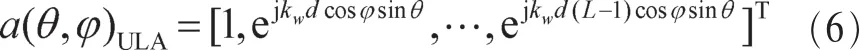
其中，φ是入射信号与水平面的夹角；θ是入射信号与垂直面的夹角；kw=2π／λ，d 为天线阵元间距；λ 为波长；L为接收端天线数目；［·］T表示矩阵转置。对于半径为r的UCA，其空间导向矢量为：

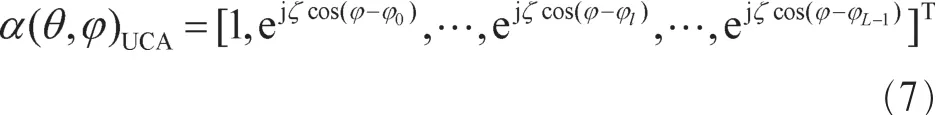
其中，ζ=kwrsinθ，φl=2πl／L，l=0，1，…，L-1。

本文选取表2中的非视距场景对均匀线性阵列和均匀圆形阵列的相关性进行仿真比较。对于二维阵列，取水平到达角平均均方根角度扩展为35.5°，水平到达角的均值为0°，对于三维阵列，增加了垂直面到达角影响，仿真中选取均方根角度扩展为7.6°，垂直到达角均值为0°。阵元和间的距离从0变化到波长的4倍，图6是2D和3D的ULA和UCA的m和n间信道相关性的比较。从图6可看出，3D天线阵列的信道相关系数比2D大，考虑垂直面内的电波贡献时，其信道的空间相关性增大。当天线单元间隔半个波长时，2D和3D ULA信道相关系数分别约为0.2和0.5，2D和3D UCA信道相关系数分别约为0.1和 0.9。

下面对仿真平台生成的3D MIMO和2D MIMO信道矩阵进行信道相关性的仿真对比。本文计算了UMi NLOS场景下8×8的MIMO信道相关性，其中，ULA和UCA天线单元之间的间隔为半个波长。从图7可以看出，当两个天线单元间隔增大时，其信道相关性变小。3D MIMO天线的互信道相关系数比2D MIMO大。两个天线单元信道互相关系数在3D时最大值大于0.9，而在2D ULA时其最大值小于0.7，在2D UCA时其最大值约为0.8。对MIMO信道相关性的仿真结果与理论计算较为吻合。

4.3 信道容量

3D MIMO信道容量不仅受收发端天线数目的影响，还会受到其传播信道的的影响。N个发射天线和M个接收天线的MIMO信道容量计算式为［11］：

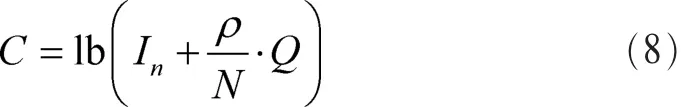
其中，ρ为信噪比，n为M和N的最小值，当N≥M时，Q=X·XH，当 N＜M 时，Q=XH·X，X 为归一化信道。

依据2D MIMO和3D MIMO的仿真矩阵，本文对ULA 2×2、4×4和 8×8阵列的 2D MIMO 和 3D MIMO 信道容量进行了仿真比较，仿真结果如图8所示。从图8可看出，2D MIMO和3D MIMO的信道容量均随着天线数目的增加而增加。当信噪比为30 dB时，对于8×8的MIMO系统，3D MIMO 的信道容量比 2D MIMO 提高了 9～10 bit／（s·Hz）；对于4×4的MIMO系统，3D MIMO的信道容量比2D MIMO提高了 5～6 bit／（s·Hz）；对于 2×2 的 MIMO 系统，3D MIMO比 2D MIMO 提高了 3～4 bit／（s·Hz）的信道容量。因此垂直面内电波的贡献对信道容量有较大影响。对于UCA阵列，3D MIMO对信道容量和ULA有类似的改善。

5 结束语

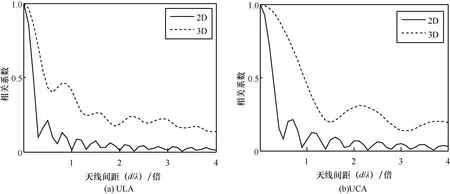
图6 2D MIMO与3D MIMO信道相关性理论分析比较

本文在WINNER信道模型的基础上开展了对3D MIMO信道建模和仿真研究，针对城市微小区场景进行了仿真验证，并对3D MIMO和2D MIMO信道模型进行了仿真分析，比较了该场景下它们的均方根时延扩展、空间相关性和信道容量。仿真结果表明：考虑电波空间垂直维度，其均方根时延扩展、阴影衰落和莱斯因子变化较小，信道的相关性将变大，但总的信道容量会有较大幅度的提升，主要原因是3D环境存在更多的散射体，子信道的总数会增加。由于缺乏3D MIMO实测数据，本文关于信道的相关性和容量只开展了理论和仿真比较研究，其结论还有待于实验结果的进一步验证。

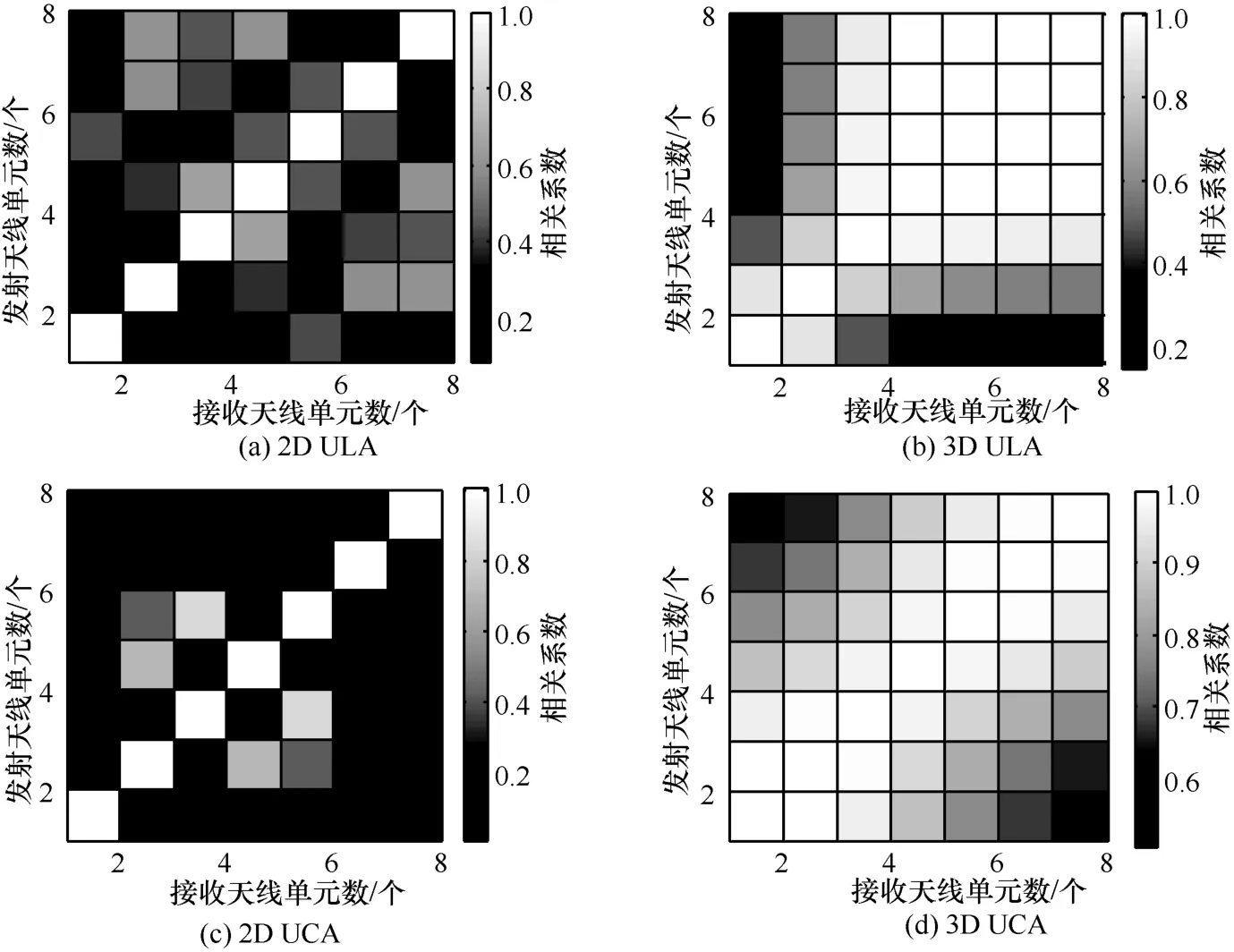
图7 2D MIMO与3D MIMO信道相关性仿真比较

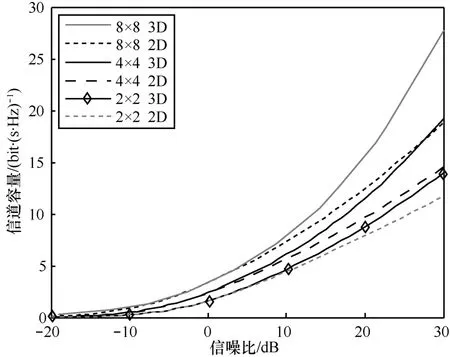
图8 2D MIMO与3D MIMO信道容量比较

［1］3GPP.Spatial channel model for multiple input multiple output simulations：TR 25.996 V6.1.0［S］.2003.

［2］PEKKA K，JUHA M，LASSI H，et al.WINNER II channel models ［EB／OL］. （2007-11-30）［2016-04-03］.http：／／max.book118.com／html／2016／0327／38935798.shtm.

［3］LIU L F，CLAUDE O，HANEDA K，et al.The COST 2100 MIMO channel model［J］.IEEE Wireless Communications，2012，19（6）：92-99.

［4］3GPP.Spatial channel model for MIMO simulations：TR 25.996 V11.0.0［S］.2012.

［5］3GPP.Study on 3D channel model for LTE：TR 36.873 ［S］.2015.

［6］JUHA M，PEKKA K，LASSI H，et al.WINNER+final channel models，deliverable D5.3 V1.0［EB／OL］. （2007-11-30）［2014-04-16］.http：／／wenku.baidu.com／link？url=aJd8OeoqXHH-xINmsvgFVqj68 PCMCK_RIgOUvZyYgVDXL68 nTEYVY9RO8id5 h6tvmIlTNDEz V8kMgt6SlsPeSIWfjF0n_ES5H3VruAmM7Gm.

［7］ZHANG J H，PAN C，PEI F，et al.Three-dimensional fading channel models：a survey of elevation angle research ［J］.IEEE Communications Magazine，2014，52（6）：218-226.

［8］XIANG C，BO Y，LIU Q Y，et al.Communication in the real world：3D MIMO［J］.IEEE Wireless Communications，2014，21（4）：136-144.

［9］裴峰.基于测量的3D MIMO空域信道建模方法研究［D］.北京：北京邮电大学，2013.PEI F.3D MIMO spatial channel modeling research based on radio channel measurement ［D］.Beijing：Beijing University of Posts and Telecommunications，2013.

［10］SU K Y，THOMPSON J S.Three-dimensional spatial fading correlation models for compact MIMO receivers ［J］.IEEE Transactions on Wireless Communication，2005，4（6）：2856-2869.

［11］PAN S，DURRANI S，BIALKOWSKI M E.Capacity of doubly MIMO systems for spatial channel model scenarios［D］.Canberra：the Australian National University，2006.

3D MIMO channel modeling and simulations

ZHAO Xiongwen1，2，3，ZHANG Mengyuan1，ZHANG Rui2，LI Shu1，LIN Leke2
1.North China Electric Power University，Beijing 102206，China 2.National Key Laboratory of Electromagnetic Environment，China Research Institute of Radiowave Propagation，Qingdao 266107，China 3.National Key Laboratory of Mobile Communications，Southeast University，Nanjing 210096，China

The existing MIMO channel simulation models are based on two-dimensional （2D）plane and can’t match with a three-dimensional （3D）radio propagation environment.A 3D MIMO channel simulation platform based on WINNER channel model was set up.After adding the vertical dimension in the model，the array patterns should be extended from 2D to 3D and 3D MIMO channel simulations were implemented.The simulation results of 3D MIMO channel parameters were validated by comparisons with the 3D measurements for an urban micro cell，good agreements could be observed.Simulation results show that the 3D channel correlation is bigger than 2D，however，its capacity has bigger improvement compared with 2D.

3D MIMO，channel simulation，channel parameter，spatial correlation，channel capacity

s：Open Research Fund of National Key Laboratory of Electromagnetic Environment （No.201400009），Open Research Fund of National Mobile Communications Research Laboratory，Southeast University （No.2016D09）

TN011

10.11959／j.issn.1000-0801.2016210

2016-06-02；

2016-08-01

电波环境特性及模化技术国防科技重点实验室开放研究基金资助项目（No.201400009）；东南大学移动通信国家重点实验室开放研究基金资助项目（No.2016D09）