地球敏感器成像仿真与检测方法

张笃周

(1.哈尔滨工业大学 航天学院，150001 哈尔滨；2.北京控制工程研究所，100190 北京)



地球敏感器成像仿真与检测方法

张笃周1,2

(1.哈尔滨工业大学 航天学院，150001 哈尔滨；2.北京控制工程研究所，100190 北京)

针对地球敏感器的设计与仿真需求，研究了地球椭球成像、大气轮廓、晨昏线及背景星空成像，实现了高精度地球敏感器成像仿真；并在此基础上比较实验了圆拟合、椭圆拟合等不同地球边界拟合及地心检测算法的性能，根据系统在轨运行特点，提出了分步地球图像检测算法.一方面克服单纯圆拟合方法带来的地球扁率误差，另一方面利用轨道先验知识克服椭圆拟合过程中的长轴不稳定性.仿真实验证明，该方法有效地提高了敏感器检测精度及系统鲁棒性，并且时间复杂度低，满足在轨要求，能够有效促进各型地球敏感器的性能提升.

地球敏感器；成像仿真；椭圆拟合；目标检测；误差分析

多视场星/地球敏感器通过在透镜系统前安装分束装置，将视场偏转为多个方向，通过共用成像系及信号处理系统，实现对恒星、地球的同时成像、检测，降低了设备体积和功耗，已在当前航天领域得到广泛应用.近年来，国内众多科研机构在该领域进行了深入的研究和实践，先后研制了涵盖不同轨道高度、不同视场形式、不同成像波长等多种地球[1-3]、月球敏感器[4].“对视场成像进行精确仿真，并进行有针对性的算法设计”已成为各类成像式敏感器设计过程中的共性、关键性问题.文献[5-6]首次系统讨论了大气散射的计算模型，根据大气密度变化来仿真大气散射效果，能够有效仿真敏感器观测结果.文献[7-9]则进一步改进了散射模型并应用到不同星球大气的仿真中.在地球敏感器成像检测方法中，文献[10]利用低分辨可见光成像，通过检验地球中心到边缘的距离搜索最优圆心，方法稳定可靠.当前，随着CCD传感器性能的不断提高，新型星敏感器的分辨率已经达到1 024×1 024以上，以地球同步轨道为例，地球扁率造成的边界偏移可达3像素左右，采用已有圆拟合模型无法克服偏移误差，只有构建有效的椭圆拟合算法才能进一步提升地心矢量的检测精度.文献[11]为进一步提高地心检测精度，提出根据已知轨道参数，估计地球长轴方向，利用长轴信息将椭圆边界点映射到圆周上，一定程度上提高了拟合精度.文献[12-13]在物理仿真的基础上，研究了针对微小卫星的可见光地球敏感器，相对于物理仿真，本文研究通过软件仿真，以进一步研究敏感器对于地球表面、轮廓特征、星月背景干扰的适应性.本文在系统分析敏感器成像检测的关键环节的基础上，借鉴航天员模拟器等[7]已有仿真方法，着重研究高精度椭球成像模型、地球大气轮廓成像仿真、晨昏线仿真方法，构建了具有通用性的地球敏感器成像仿真平台，并应用到北京控制工程研究所某型敏感器研发中，依托该平台对不同地心检测算法进行比较分析，根据系统在轨运行特点，提出了一种分步地球图像检测算法，一方面克服单纯圆拟合方法带来的地球扁率误差，另一方面利用轨道先验知识克服椭圆拟合过程中的长轴不稳定性.有效缩短地球敏感器的研制周期、显著提升了检测性能及系统可靠性.

1 地球敏感器仿真计算模型

如图1所示，地球敏感器仿真计算可分为“地球光学建模”、“相机成像建模”、“图像检测算法”3部分.其中相机成像建模是一个通用问题，本文着重讨论与敏感器问题具体相关的地球光学建模及相应的图像检测算法.

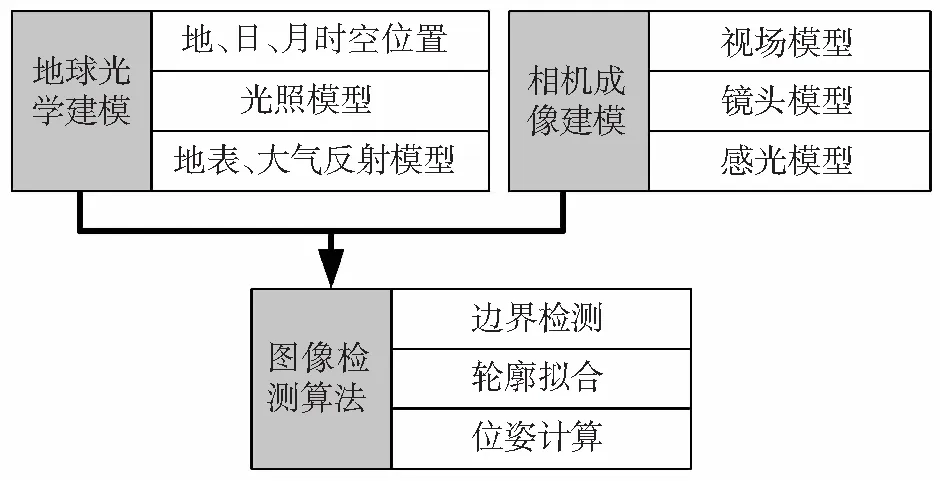
图1 地球敏感器仿真

1.1 地球敏感器成像仿真

成像式地球敏感器首先检测地球轮廓边缘，然后进行拟合，从而得到地球地心矢量.对于大气轮廓成像的准确仿真，是各型敏感器设计实验的难点和关键.文献[5]系统地讨论了地表反射、大气散射作用下的成像仿真，较好模拟了外太空对地观测形态，文献[7]则在此基础上进一步探讨了通过GPU提高算法实时性，并用于航天员训练仿真.本文在借鉴文献[7]的基础上，根据地球敏感器的检测特点，一方面忽略水面、云层建模等对于精度影响较小的地物目标仿真，另一方面加入了对于地球轮廓的精确描述，构建适用于敏感器算法测试的图像仿真系统，主要考虑3方面因素：

1)地球形状. 地球是一个低扁率的椭球体，不考虑地球扁率的情况下，将导致敏感器精度下降，因此在仿真过程中，必须呈现不同视角下椭球轮廓投影.

2)地、日、月时空位置及光照模型.地、日、月的空间位置及太阳光照模型是地球轮廓、晨昏线仿真的基础.通过月球及恒星仿真，模拟背景星空对敏感器的干扰.

3)地表、大气反射模型.由于地球大气的存在，形成了一个对太阳光线反射、散射、吸收的复杂过程，造成地球轮廓边界的模糊过渡，这一干扰直接影响地球轮廓的检测精度.

1.2 地心检测算法研究

地心检测算法主要分为边界点检测、圆/椭圆拟合两部分.在边界点检测过程中，关键在于克服地球大气轮廓造成的光晕干扰.圆拟合、椭圆拟合等一般性问题在图像处理、应用数学等领域已得到深入研究，具体到地球边缘拟合上，具有以下特点：地球扁率低，加之受到大气轮廓的干扰，采用圆拟合鲁棒性高而精度低，采用椭圆拟合精度高但鲁棒性低.如何利用轨道特点及先验知识，从系统的角度提升地心矢量的计算精度是敏感器图像处理算法的关键.

实际应用中，轨道参数误差将对检测算法精度产生影响.本文基于图像仿真平台，模拟不同参数误差下的成像状态，进而比较分析不同拟合算法精度及鲁棒性，为算法的优化选择提供数据支持.

2 地球成像仿真数学模型

如图2所示，构造地球椭球模型，然后基于光路可逆原理，将像素v逐点映射到椭球模型上，获取像素亮度.映射过程分为3种状态：1)映射到地球表面u，则根据u点的光照状态确定亮度；2)映射到大气边缘，则根据大气边缘光照部分u1-u2散射状态确定亮度；3)当v点未能映射到地球上，则为图像背景(月球、恒星)部分.

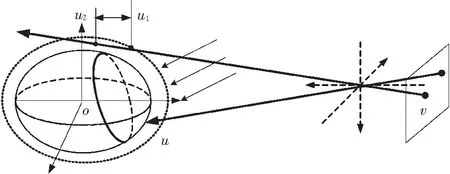
图2 椭球轮廓成像

本系统中，儒略日、恒星时计算采用International Astronomical Union提供的开源代码SOFA.太阳轨道计算采用Paul Schlyter的中等精度计算方法，月球轨道计算采用Astronomical Algorithms所述算法实现，地球纹理及星表可根据需要进行更换.图像仿真的关键就在于从v到u的轮廓投影及u点的亮度估计.

2.1 轮廓投影

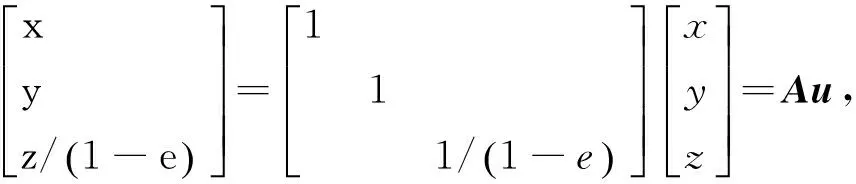
设敏感器坐标到目标本体坐标系的变换为uo=Tos(us-dos)，令mo=Tosdos，则有

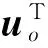
(1)

整理得到关于α的二次方程

令：

要使α有解，解得到成像区域方程为

(2)

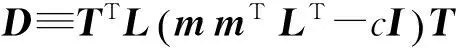
(3)

时，v属于成像区域，对应的球坐标为

2.2 亮度估计

影响成像亮度的因素主要有:1)太阳距离及入射角度；2)u处的光线吸收性质.

曲面法向量为

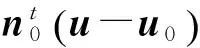
式中s为太阳中心向量，当cosβ=0时为晨昏线.当无遮挡时，该处光强为Icosβ，亮度I的计算采用文献[5-6]中的方法

地球大气轮廓是一个与地球扁率相同，半径增加的椭球，适用以上方程.采用以下步骤计算大气成像：

1)大气边缘判断.根据式(2)计算像点是否属于大气轮廓且不属于地球表面;

2)亮度估计.如果属于大气边缘，则根据式(3)中的D值，估计大气厚度(方程两根间的距离).

2.3 成像仿真试验

如图3所示，成像仿真流程分为背景星空仿真、地、月、日仿真、视场叠加3部分.

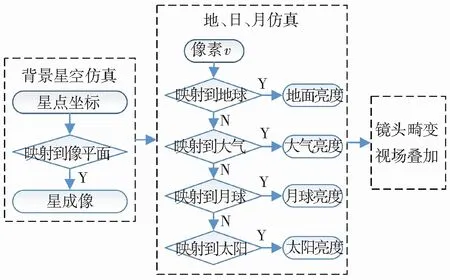
图3 地球成像仿真流程示意

背景星空仿真中，利用星表计算个星点坐标是否能投射到像平面上，如果能，则根据星等进行亮度仿真.地、日、月仿真中，根据轮廓投影描述的光路可逆过程，逐像素计算点v的投影坐标，顺序判断是否映射到地球、大气轮廓、月球、太阳，并按映射类型进行亮度仿真.最后进行镜头畸变及多视场叠加.

通过修改矩阵L，可以仿真地、日、月等不同任意形式的二次曲面.采用从像点到地球的逐点映射模型，其优点在于可以以任意精度生成仿真图像，敏感器图像仿真的关键就在于地球轮廓的准确描述.因此v点映射到地球轮廓附近时，对其进行亚像素插值，获取高分辨的图像，然后滑动滤波获取逼真的平滑边界.

仿真效果如图4所示，从图4(a)、(b)对比可以看出，相对于google Earth，该算法能够生成更加真实、平滑的大气轮廓.从图4(c)、(d)对比中，可以看出，算法能有效仿真晨昏线，但云层、气旋等大气变化则相对单调，进一步改进中，可以构建单独的云层贴图与地形纹理贴图配合使用.

该方法的缺点在于需要逐点计算、运算量大，利用Intel i7 2.4 G CPU不做深度优化的情况下，单帧1 024×1 024图像仿真时间为0.4 s，测试前，通常需要根据预设参数，事先生成样本集，不适用于一些实时性高的场合.

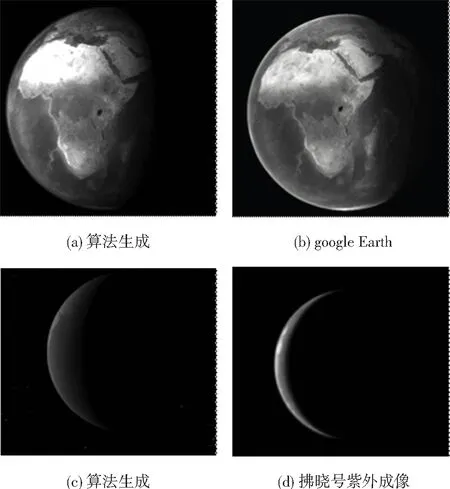
图4 仿真图像示意

3 地心检测

地球敏感器的测量原理及过程详见文献[14-15]，本文重点研究地球图像中的地心检测问题，流程如图5所示，主要分为“初步圆拟合”和“二次椭圆拟合”两个过程.

初步圆拟合中，快速搜索到若干地球轮廓边界点，进行圆拟合，获取初步圆心半径；二次椭圆拟合中，搜索圆周轮廓边界，剔除野点后进行椭圆拟合，以获得高精度的地心坐标及地球半径.

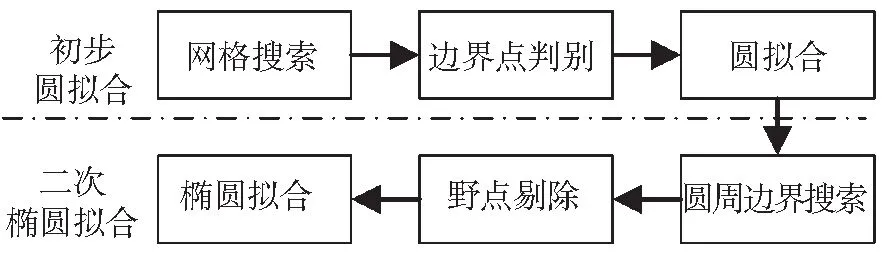
图5 地心检测流程示意

3.1 地心初定位

网格搜索如图6(a)所示，在图像上以一定间隔利用Sobel算子做水平/垂直搜索，找到候选边界点.然后对各点邻域特征进行进一步判别.文献[7]对判别规则进行了详细讨论，主要包括：前景点数、背景点数、前景背景灰度均值差、前景背景中心距离，利用这些规则可以剔除大部分的恒星干扰、地球纹理干扰以及晨昏线干扰.

判别出有效边界点后，进行圆拟合，以初步确定圆心、半径.该环节的关键在于保证各种干扰环境下的算法的鲁棒性.因此采用Hough变换的思想进行计算：任意3点拟合一个圆，检测其他点到该圆心的距离，小于误差阈值则投票，投票最多的圆为拟合结果，其优点在于鲁棒性强、野点超过70%时也能有效拟合，因而能有效识别、剔除晨昏线.

该方法的缺点在于运算量大，算法实现过程中，根据轨道先验，仅选取相互距离较大的点进行拟合测试，并采用部分投票等方法，能减少运算量.

在敏感器连续运行过程中，利用前后帧图像的相关性，即可获得圆心大致位置信息.初定位仅用于初始帧的检测，实时性要求不高，因此采用该运算量大、但鲁棒性高的算法是恰当的.

3.2 二次拟合

圆周边界搜索如图6(b)所示，获取地球轮廓大致位置信息后，在轮廓附近，顺序获取地球边界点.相比网格搜索得到的边界点，顺序边界点具有以下优点：仅在轮廓附近搜索、干扰少；边界点彼此相邻、相关有序.

利用这些信息，在圆周边界点中进一步甄选出最稳定、可靠的点进行椭圆拟合：1)边界强度统计.对边界强度进行直方图统计，剔除异常点;2)边界位置判别.计算边界点到圆心之间距离，剔除异常点；3)相关性判别.相邻边界点的边界强度及到圆心距离不应产生跳变，否则剔除.

利用椭圆模型进行拟合，可以克服圆拟合带来的扁率误差.但由于地球扁率低，直接椭圆拟合难以准确估计椭圆长轴方向，导致精度严重下降，尤其是在地球可见弧段较短时，无法保证鲁棒性，因此需要引入先验知识，给出长轴方向后，再进行拟合.

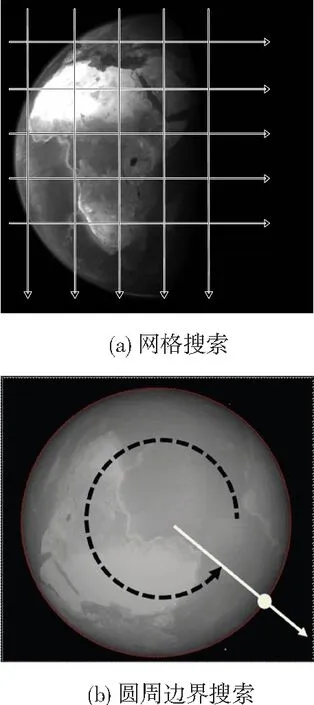
图6 地球边界检测示意

4 地心检测试验

针对某型高轨道卫星为例进行试验，对比实验已知长轴方向和未知长轴方向下的椭圆最小二乘拟合，参数设定如下：地球敏感器设定为正交双视场传感器，图像分辨率1 024×1 024.网格搜索设定为36×36，圆周边界搜索设定为360个点.

利用图像仿真生成样本：为测试在卫星偏航角未知，即图像中地球椭圆模型长短轴方向未知的情况下，算法的精度.设定卫星偏航角设定为0.5°、1.0°、2.0°、3.0°产生4组样本，以模拟卫星轨道的误差.

敏感器大部分时间不能得到完整的地球边缘，且不同时刻对应的弧长不同、不同的季节对应的弧段位置不同，考虑不同季节太阳照射位置不同，将弧段位置分为春、夏、秋、冬4个季节，每个季节样本1 000张，合计4 000张；考虑不同轨道高度，设定为3～4×104km，每间隔2 000km为一级，每组合计6级共计24 000张样本.

根据样本可见轮廓的长短进行分类，可见轮廓大于2/3的为整圆，1/3～2/3的为半圆，统计圆心坐标误差及半径误差.分别对3种方法进行实验：1)最小二乘圆拟合实验，结果见表1；2)未知轨道先验知识的椭圆拟合：假设椭圆长轴方向未知、扁率未知，直接进行五参数椭圆拟合测试，结果见表2；3)已知轨道先验知识的椭圆拟合：假设椭圆长轴方向已知、偏航角为0、扁率已知.进行三参数椭圆拟合，结果见表3.

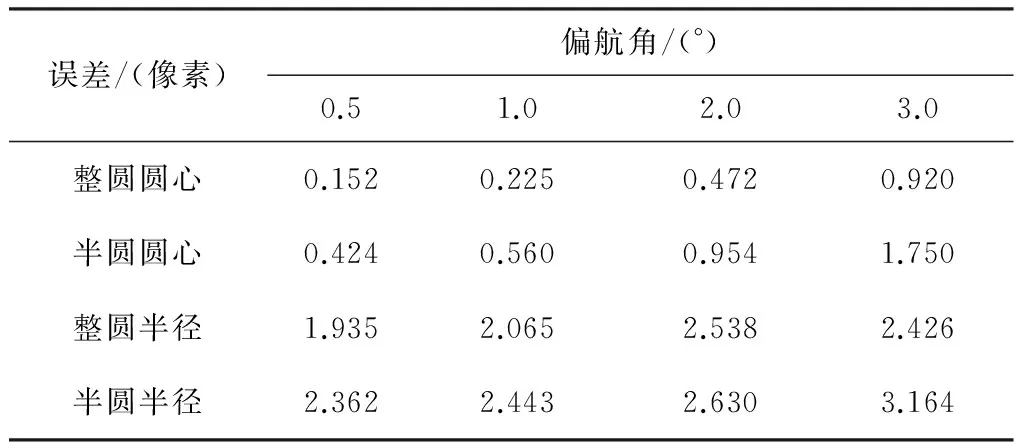
表1 算法1——圆拟合误差

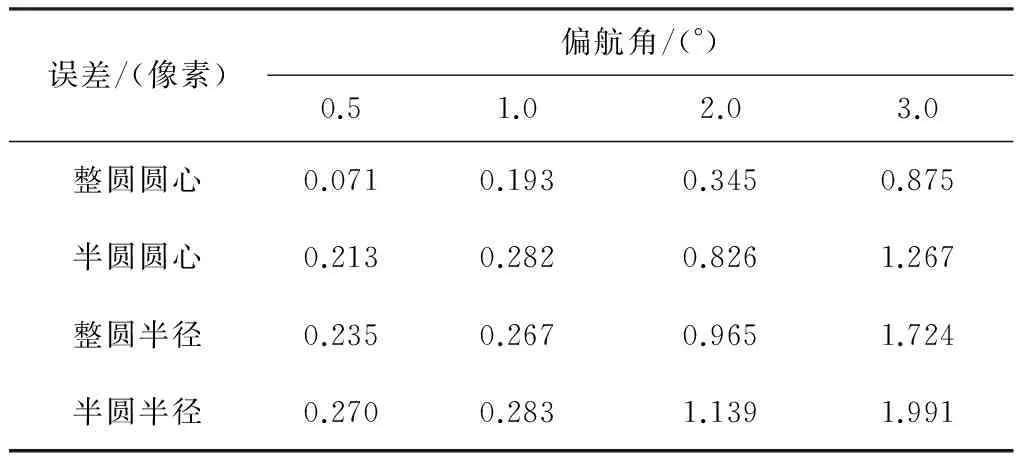
表2 算法2——未知长轴方向的二次拟合误差

通过以上算法比较看出，圆拟合方法对于整圆圆心估计精度尚可，但对于半径估计误差较大，尤其是偏航角增大时.与之相比，对于算法2当长短轴未知时，直接进行椭圆拟合精度较差，尤其是半圆情况下.这与已有文献[10-11]中提出的椭圆鲁棒性差的观点是一致的.分析其原因，由于椭圆拟合未能正确找到长轴方向，错误椭圆模型非但不能带来拟合精度的提高，相反将导致误差放大，这也是已有文献中，不建议直接采用椭圆拟合的原因.对于算法3，利用了轨道先验知识，并模拟了实际的误差状态，在小角度偏航角的情况下，利用先验知识确定轨道长轴及扁率.在长轴方向误差较小时，椭圆模型依然能提高拟合精度.因此在实际应用中，利用先验知识可以有效保证椭圆算法鲁棒性.

表3 算法3——已知长轴方向的二次拟合误差

实验过程中，根据轮廓长度(有效边界点数)与圆周长度的比例，统计不同比例下的地球中心拟合误差及地球半径拟合误差，如图7所示.从图7中可以看出，当可见轮廓超过40%时，现有算法能较准确计算中心，当可见轮廓超过80%，误差基本控制在0.1像素以下.当可见轮廓少于30%时误差迅速增大.半径拟合误差在可见轮廓大于35%时基本保持稳定.可见轮廓小于30%时，误差增大，但相对中心误差增速较缓慢，可见在可见轮廓较低时，中心误差是算法的主要问题.

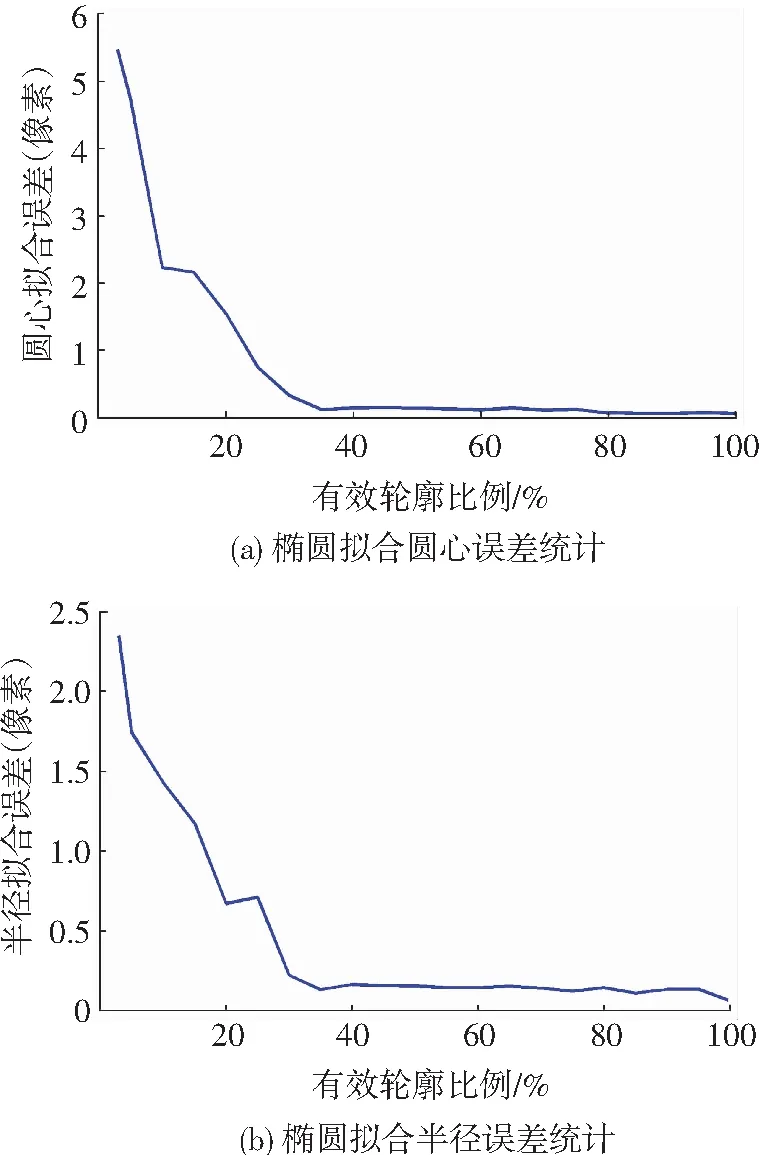
图7 拟合误差统计分析

5 结 论

1)针对地球敏感器检测算法的特点，研究地球椭球成像、大气轮廓、晨昏线及背景星空成像，构建了高精度地球成像仿真平台.

2)在地球成像仿真平台上，验证测试了针对不同应用场合的敏感器算法，并根据卫星在轨运行特点，提出了分步地球图像检测算法.该方法一方面克服单纯圆拟合方法带来的地球扁率误差，另一方面利用轨道先验知识克服椭圆拟合过程中的长轴不稳定性.实验证明，在卫星存在小角度偏航角误差的情况下，采用椭圆拟合依然能够有效提高了敏感器检测精度及系统鲁棒性.通过构建该图像仿真及算法测试平台，将有效缩短各型敏感器的研发周期、保障产品质量.

[1] 孙俊, 张世杰, 李葆华. 利用地球紫外和恒星可见光的卫星自主导航[J]. 光学精密工程, 2013, 21(5): 1192-1198.

[2] 叶生龙, 魏新国, 樊巧云,等. 多视场星敏感器工作模式设计[J]. 北京航空航天大学学报, 2010, 36(10): 1244-1247.

[3] 沈国权, 王昊, 郭振东,等. 面向微小卫星的红外静态焦平面地球敏感器设计[J]. 传感技术学报, 2012, 25(5): 571-576.

[4] 黄欣, 王立, 卢欣. 嫦娥一号卫星紫外月球敏感器[J]. 空间控制技术与应用, 2008, 34(1): 51-55.

[5] NISHITA T, SIRAI T, RADAMURA K, et al. Display of the earth taking into account atmospheric scattering[C]// Proceedings of the 20thAnnual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 1993: 175-182.

[6] CORNETTE W M, SHANKS J G. Physical reasonable analytic expression for the signle-scattering phase function[J]. Applied Optics, 1992, 31(16): 3152- 3160.

[7] 杜芳, 张炎, 晁建刚,等.基于GPU的地球大气散射现象可视化仿真[J].系统仿真学报, 2009, 21(s2): 147-150.

[8] 刘维敏, 蓝朝桢, 卢战伟, 等. 火星大气实时仿真技术研究[J]. 深空探测研究, 2008, 6(4): 15-18.

[9] 廖瑛, 刘光明, 文援兰. 卫星星敏感器视场建模与仿真研究 [J] .系统仿真学报, 2006, 18(s2) :38-44.

[10]SEKIGUYCHIT, YAMAMOTO T, IWAMARU Y. Three-axis attitude estimation experiments using ccd earth sensor[J]. Journal of Space Technology & Science A Publication of Japanese Rocket Society， 2004, 20(1):16-23.

[11]KUHL C T F．Combined Earth-/Star Sensor for attitude and orbit determination of geostationary satellites [D]. University Stuttgart: Institute for Flugmechanik und Flugregelung, 2005.

[12]郭振东，王昊，应鹏，等.面向微小卫星的可见光地球敏感器设计[J].传感技术学报，2012，25(10):1400-1405.

[13]SI M,BENYETTOV M,BENTOUTOU Y,et al. Three-axis active control system for gravity gradient stabilized microsatellite[J].Acta Astronautica,2009,64(7/8):769-809.

[14]钱勇.高精度三轴稳定卫星姿态确定和控制系统研究[D]．西安：西北工业大学，2002.

[15]王鹏.基于星载敏感器的卫星自主导航及安全确定方法研究[D].哈尔滨：哈尔滨工业大学，2008.

(编辑 张 红)

Imaging simulation and processing of Earth sensor

ZHANG Duzhou1,2

(1.School of Astronautics, Harbin Institute of Technology, 150001 Harbin，China; 2.Beijing Institute of Control Engineering, 100190 Beijing，China)

An imaging simulation system of Earth Sensor is investigated, including the imaging of earth, atmosphere, twilight lines and background stars. To improve the simulation accuracy, the outline of earth is described as an ellipsoid rather than a sphere, and the scattering of atmosphere is taken into account. Based on the simulator, a hierarchical ellipse fitting algorithm is studied, in which the ellipse model is constructed to reduce the fitting error caused by the flat rate of earth, and the orbit a priori knowledge is used to improve the fitting robustness. Numerical simulations demonstrate the effectiveness of the approach proposed.

Earth sensor；imaging simulation；ellipse fitting；target detection；error analysis

10.11918/j.issn.0367-6234.2016.04.007

2014-10-17.

国家自然科学基金(61402133).

张笃周(1960—)，男，研究员.

张笃周, zhangdz60@126.com.

V19

A

0367-6234(2016)04-0042-06