功率连接型数模混合仿真系统接口特性分析

周艳华,聂冰青

(1.东北电力大学 电气工程学院,吉林 吉林 132012； 2.国电南京自动化股份有限公司,南京 211100)



功率连接型数模混合仿真系统接口特性分析

周艳华1,聂冰青2

(1.东北电力大学 电气工程学院,吉林 吉林 132012； 2.国电南京自动化股份有限公司,南京 211100)

为解决功率连接型数模混合仿真中闭环稳定性与仿真精确性两个关键问题,提出基于系统传递函数的稳定性分析方法和精确性评估方法。介绍并比较了5种接口算法的特性,研究论证了其稳定性与精确性的优劣。在Matlab/Simulink中搭建了简单电路数字仿真子系统与物理被试系统的模型,对5种接口算法的稳定性与精确性进行了离线仿真,结果表明特定应用中阻尼阻抗法相比于其他算法可行性更高。

功率连接型数模混合仿真;接口算法;稳定性;精确性

随着计算机技术的快速发展,数模混合仿真(hardware-in-the-loop, HIL)技术在电力电子及电力系统领域得到越来越广泛的应用。由于数模混合仿真技术是一种先进的实验/测试方法,因此可在虚拟环境中反复、安全、经济地模拟新型的物理装置原型[1]。

目前大部分数模混合仿真应用均以控制装置作为物理被试系统。数字仿真系统与物理被试系统之间传输的信号为低功率的控制信号,变化范围为+10～-10 V,由A/D、D/A装置准确转换,称为信号型数模混合仿真(control hardware—in-the-loop, CHIL)。而实际应用中一些功率设备,如电动机也需要被测试。这种情况下的物理被试系统会发出或吸收有功功率,此时接口设备需包含功率放大及功率转换装置,称之为功率连接型数模混合仿真(power hardware-in-the-loop, PHIL)[2]。

在功率连接型数模混合仿真系统中,尤其是对于高功率设备,功率接口带来的误差(如延时和失真等)会引起严重不稳定问题和不准确的仿真结果。文献[3-6]介绍了将功率连接型数模混合仿真作为一种便捷工具来解决电力系统各种问题的初步试验,而未研究接口算法对系统稳定性的影响。文献[7]提出了一种基于一阶近似的新型接口算法,但未对该算法的稳定性进行详尽的理论分析。文献[8-9]提出一种一般性的实验步骤,然而只停留在理论研究层面,很难应用于实践中。以上研究均针对独立系统和特定问题,对如何实现功率连接型数模混合仿真,尤其是接口算法的选择缺乏一般性的分析。因此,本文论述了引起功率连接型数模混合仿真不稳定问题的根本原因,并比较了常用的5种接口算法,提出只有选择合适的接口算法才能得到最优仿真结果。

1 功率连接型数模混合仿真不稳定问题

闭环稳定性是功率连接型数模混合仿真中的关键问题。仿真的不稳定性不仅导致仿真结果错误,甚至会造成测试设备和物理被试系统的损坏。引起不稳定的主要原因包括接口延时、有限带宽、接口功率放大器产生的谐波等。以一个简单的功率连接型数模混合仿真系统为例(如图1所示),对其稳定性进行分析。

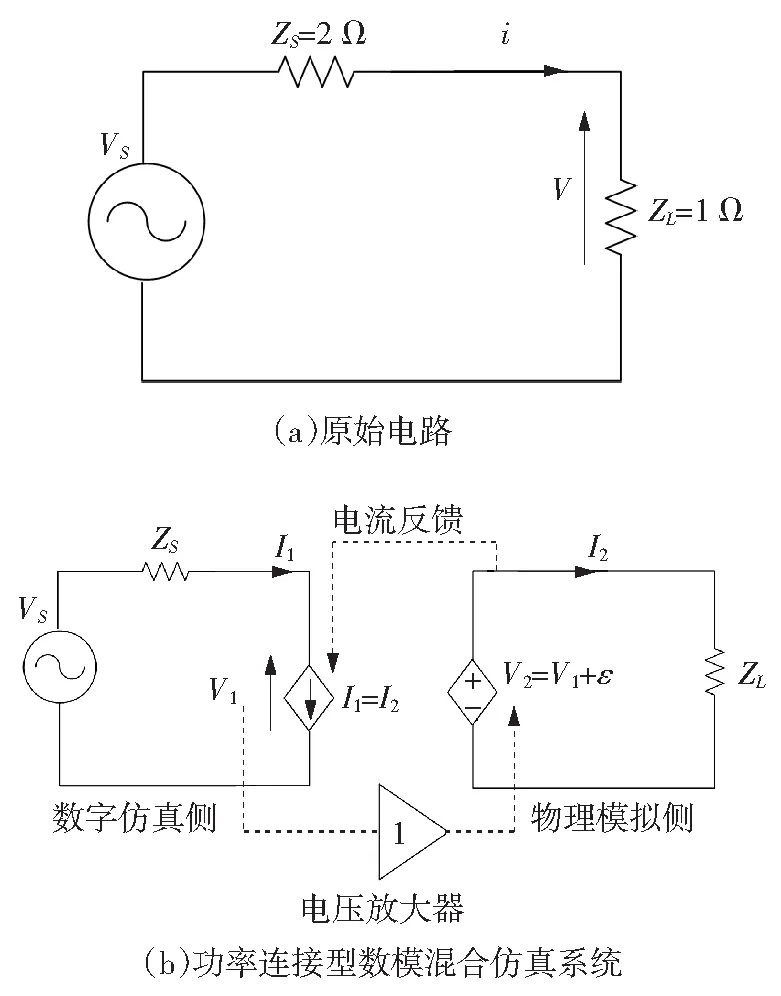
图1 数模混合仿真系统不稳定问题分析电路

原始电路为分压式电路,PHIL电路中,负载阻抗ZL为实际的硬件电阻,而电压源VS和阻抗ZS都是由数字仿真实现。为了实现这个接口,采用一个电压放大器将“数字电压V1”变为“实际的电压V2”,并加在负载电阻两端。流过负载电阻的实际电流I2通过传感器测量并反馈至数字侧,即数字侧电流源I1。尽管原始分压电路稳定,但解耦后的PHIL电路并不稳定。

假设时间tk时,V2的电压放大器产生一个误差ε,即Δv2=ε。I2=V2/ZL,则电流I2对应的误差为Δi2(tk)=ε/ZL。当电流Δi2反馈回数字侧时,进一步导致v1的更大误差,即

Δi2(tk)=ε/ZL

V1=Vs-Zs×I1

Δv1(tk+1)=-(Zs/ZL)ε

下一仿真步长更新后的V1值包含上一步长的误差Δv1,Δv1被进一步放大,系数为-(ZS/ZL)。如果ZS/ZL>1,误差的幅值将不断增大,最终导致系统失稳。

1.1 功率连接型数模混合仿真稳定性分析

功率连接型数模混合仿真系统可表示成传递函数的形式,如图2所示。

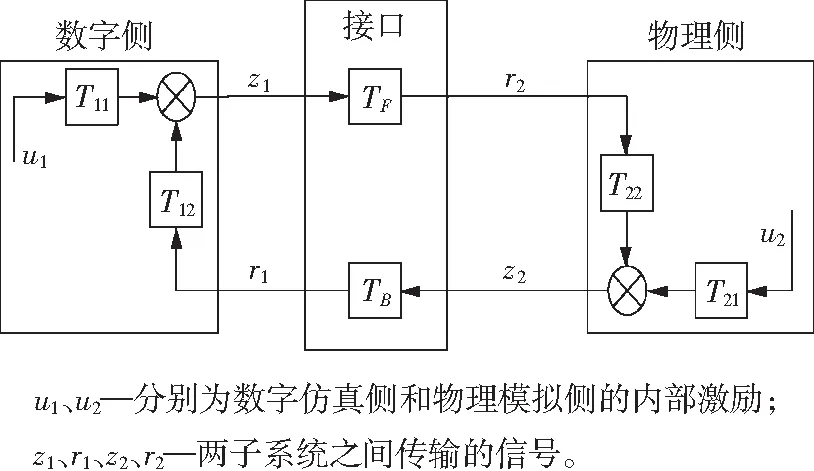
图2 传递函数形式的功率连接型数模混合仿真系统

为保证功率连接型数模混合仿真系统稳定,数字仿真子系统与物理被试子系统都必须是稳定的系统,且反馈回路必须只含有负实部的极点,即开环传递函数GOL=T12TBT22TF需满足奈奎斯特稳定判据。

将上述分析应用于图1所示系统,假设功率接口为理想接口,电压放大器以一个微小延时Δt来表示,可得到以下关系:

u1=Vs,T11=1,T12=-Zs,z1=V1

r2=V2,TF=e-sΔt,u2=0,T21=0

T22=1/ZL,z2=I2,r1=I1,TB=1

代入开环传递函数表达式可得

ZS/ZL的值为2,e-sΔt代表当系统频率增加时一个固定的相位差。开环传递函数的奈奎斯特曲线为一组半径不同的圆,无限次包含(-1,0)点,表明系统不稳定。

1.2 功率连接型数模混合仿真系统精确性分析

稳定的功率连接型数模混合系统并不能确保该系统在实际应用中可行。除稳定之外,必须保证该系统精确。由于缺乏判断精确性的参考标准,因此判断一个系统是否精确较为困难。而评估功率连接型数模混合仿真系统精确性的一个可行方法是评估考虑接口扰动时系统传递函数的响应。

假设图1所示系统中v1代表系统的状态。由于绝大多数系统的误差来源于接口电压放大器,将电压误差视为扰动并研究扰动与v1之间的传递函数,即

分析可知,正常带宽范围内TF接近于单位增益,系统的开环传递函数GOL幅值越小,系统越精确。

2 接口算法

将图1所示原始分压电路按图3所示系统进行数模混合仿真。放大的信号不再是v1,而是电流i1。测量加在负载上的电压v2并反馈至数字仿真系统。

此时系统的开环传递函数为

GOL的幅值为0.5,系统稳定。表明采用不同结构的接口拓扑可提高系统的精确性与稳定性。为区分不同拓扑结构的接口,引入接口算法的概念。接口算法定义了两个重要的特征:一是传输信号的类型,如电流、电压、功率等;二是传输信号的方式,如增益、低通滤波等。

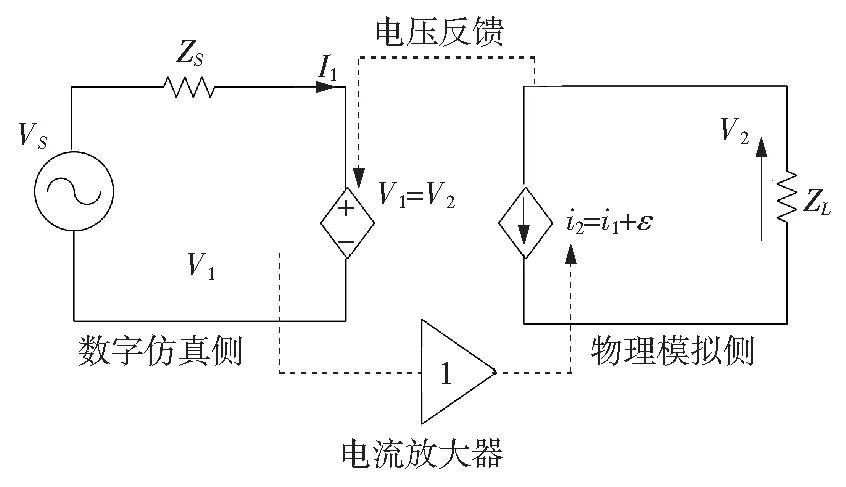
图3 放大接口电流的数模混合仿真系统

2.1 理想变压器法(ITM)

理想变压器法是进行功率连接型数模混合仿真最传统、最直接的方法之一。根据放大信号的不同分为电压型理想变压器法(见图1)和电流型理想变压器法(见图3)。假设PHIL系统误差只来源于接口放大设备的延时,则基于ITM法的系统开环传递函数可表示为

其中,ZL和ZS分别为物理被试系统和数字仿真系统的等效阻抗。该等效在实际中是可行的,因为任何时刻电力系统都可以表示成戴维南或诺顿形式。该接口的稳定性取决于ZS/ZL的值。

2.2 时变一阶近似法(TFA)

TFA是基于假设PHIL系统物理被试系统,可以视为一个一阶RL电路或一阶RC电路。结合以往历史实验数据,该模型的回归系数可以在线升级解决。在数字侧进行补偿以纠正接口带来的误差。

以RL电路为例,假设物理被试系统存在下述一阶等式:

根据梯形近似法,电流i2的值可由上一仿真步长中的电压v1和电流i2计算得到,即

i2(k)≈αv1(k-1)+βi2(k-1)

i2(k)=Geqv1(k-1)+Ieq

α、β可由下式计算:

RL型时变一阶近似法结构如图4所示。

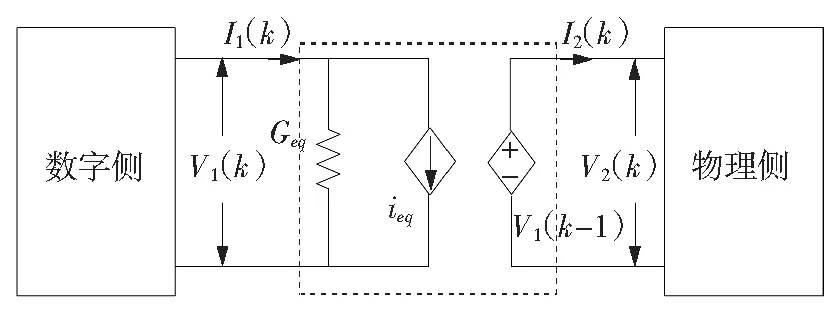
图4 时变一阶近似法接口结构

RC型时变一阶近似法与RL型特性相似。TFA算法本质上是一种预测方法,通过建立物理被试系统的模型来预测系统状态的变化。因此,和其他任何一种预测型方法一样,时变一阶近似法在处理非线性系统及高频信号时存在缺陷。

2.3 传输线模型法(TLM)

输电线模型是利用连接电感或电容对输电线路进行等效的一种方法。由于传输线可进一步用Bergeron模型表示(从电路任何一端看,线路为独立的戴维南或诺顿电路,只能看到另一端当前的参数),因此该方法适用于解耦大规模电力系统,且方便进行计算。

应用传输线模型的功率连接型数模混合仿真系统结构如图5所示。

图5 传输线法接口结构

将连接电容或电感以传输线路的Bergeron模型代替,等效电阻R1k可由下式计算得到:

式中Δt为线路行波传输时间,在功率连接型数模混合仿真中变成了接口延时。

传输线模型算法的等效传递函数为

由于TLM是严格基于梯形近似的,因此它非常稳定,然而在功率连接型数模混合仿真中很难实现。首先,该算法以一个电阻R1k代替了连接电容或电感,在高功率的数模混合仿真中,电阻将消耗大量功率。其次,R1k的参数与连接电容或电感的参数有关,当仿真系统发生变化时,R1k值随其变化,以致实现不够灵活,耗费巨大成本。最后,接口延时Δt与负载状态和信号的频率有关,假设Δt为固定值,则会导致仿真精度降低。

2.4 部分电路复制法(PCD)

PCD法来源于稀疏技术。文献[10]将该方法应用于大型电路仿真软件SPICE。PCD法将原始电路分割成多个子电路,使用迭代法求解。部分电路复制法的结构如图6所示。原始电路中的连接阻抗zab在数字侧和物理侧被重复。

图6 部分电路复制法接口结构

PCD法的开环传递函数为

(1)

由式(1)可知,对于电阻性网络,部分电路复制法比理想变压器法的稳定性更好,原因在于PCD法更容易使开环传递函数的幅值小于1。假设该方法在特定的应用中收敛,仿真精度可由足够的迭代次数保证。但在实际仿真中,每个仿真步长只能迭代一次,因此每次迭代的误差必须尽可能小。为保证仿真精度,连接阻抗zab的数值应比za和zb的值大。实际应用很难满足上述条件,因此部分电路复制法的精度一般较低。

2.5 阻尼阻抗法(DIM)

阻尼阻抗法是介于理想变压器法和部分电路复制法之间的一种方法,通过插入一个阻尼阻抗z*来实现。阻尼阻抗法的结构如图7所示。

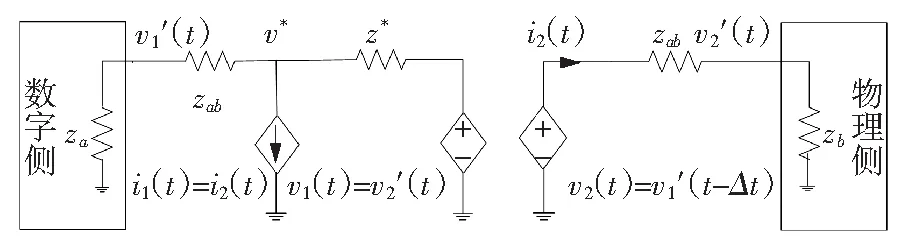
图7 阻尼阻抗法结构

由图7可知,当阻尼阻抗z*等于0时,电压v*等于v1,DIM法与PCD法相同;当z*无穷大时,DIM法变成了ITM法。根据阻尼阻抗z*的取值不同,DIM法的稳定性介于部分电路复制法和理想变压器法之间。z*的最优取值可由DIM法的开环传递函数求得:

(2)

由式(2)可知,当z*=Zb时,开环传递函数的幅值为零,则系统高度稳定。然而,很难获得Zb的准确值,因为这要求物理被试系统为理想模型,所以实际应用中并不存在。但可由上一步仿真结果计算出Zb的近似值,可由仿真得到的v2′和i2的有效值计算出Zb的平均值。尽管阻抗元件的增加会带来损耗,但阻尼阻抗法仍很大程度地改善了系统稳定性和精确性。

3 仿真验证

3.1 仿真算例

以图8所示的简单电路为例,在Matlab/Simulink中分别搭建了数字仿真子系统与物理被试子系统模型,进行了数模混合仿真的离线验证,并与理论分析进行了对比。仿真步长设为60 μs,接口延时取500 μs。

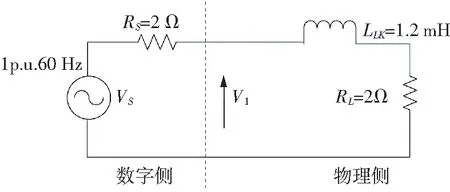
图8 用于数模混合仿真的简单电路

系统稳态运行时的波形如图9所示。

图9 RS=2 Ω时,不同接口算法的数模混合仿真对比图及局部放大图

由图9可知,传输线法和部分电路复制法波形误差较大,而其他算法的结果相对准确。当RS的值增加到5 Ω时,传输线法和理想变压器法使系统仿真不稳定。同时传输线法和部分电路复制法的仿真结果仍然误差较大,而阻尼阻抗法依然保持较高的稳定性与精度,如图10所示。

3.2 分析对比

通过理论分析与仿真验证,将5种接口算法的特性总结如下:

图10RS=5 Ω时,不同接口算法下的数模混合仿真对比图及局部放大图

Fig.10RS=5 Ω, comparison chart and partial discharge of different interface algorithm for digital analog mixed simulation

1) 理想变压器法作为最传统、最直接的方法,精度高但稳定性相对较低。

2) 传输线法和部分电路复制法具有较高的稳定性,但其精确性过度依赖于连接元件的参数及电源电阻和负载电阻的比例。此外,传输线模型要求原始电路中存在连接电容或电感进行等效解耦,并在数模混合仿真的数字仿真系统及物理被试系统中加入电阻元件,在许多应用中,电阻元件的增加限制了该方法的可行性。

3) 时变一阶近似法使用预测方法以补偿接口延时,但该方法稳定性较低,且接口中存在大量噪声,实现起来不够灵活。

4) 阻尼阻抗法结合了理想变压器法和部分电路复制法的优点。当z*接近物理被试系统的阻抗值时,该方法具有较高的稳定性与精确性,适用于绝大多数功率连接型数模混合仿真系统。

4 结 语

为保证功率连接型数模混合仿真的可靠性与安全性,本文提出通过奈奎斯特稳定判据判断系统稳定性方法。详细分析并比较了5种接口算法特性。在Matlab/Simulink中搭建了简单电路数字仿真子系统与物理被试系统的模型,对5种接口算法的稳定性与精确性进行了离线仿真。结果表明:尽管不存在适用于所有功率连接型数模混合仿真的最优接口算法,但与其他算法相比,阻尼阻抗法的稳定性与精确性更高。

[1] 周俊,郭剑波,朱艺颖,等.特高压交直流电网数模混合实时仿真系统[J].电力自动化设备,2011,31(9):18-21.

ZHOU Jun,GUO Jianbo,ZHU Yiying, et al.Digital-analog hybrid real time simulation system of UHVDC and UHVAC power grid[J]. Electric Power Automation Equipment 2011,31(9):18-21.

[2] 胡昱宙,张沛超,包海龙,等.功率连接型数字物理混合仿真系统(一)接口算法特性[J].电力系统自动化,2013,7(37):36-42.

HU Yuzhou,ZHANG Peichao,BAO Hailong, et al.Power hardware-in-the-loop simulation system. part one characteristics of interface algorithms[J]. Automation of Electric Power Systems,2013,7(37:):36-42.

[3] ACHA E, ANAYA-LARA O, PARLE J, et al. Real-time simulator for power quality disturbance applications[J].Harmonics Quality Power,2000,4(3): 763-768.

[4] ZHU W, PEKAREK S, JATSKEVICH J, et al. A model-in-the-loop interface to emulate source dynamics in a zonal DC distribution system[J].IEEE Trans.Power Eletron,2005,2(20):438-445.

[5] VIEHWEIDER A, LAUSS G, FELIX L. Stabilization of power hardware-in-the-Loop simulations of electric energy syste-ms[J]. Simulation Modelling Practice and Theory, 2011,19(7):1699-1708.

[6] REN W, STEURER M, BALDWIN T L. An effective method for evaluating the accuracy of power hardware-in-the-loop simulations[J]. IEEE Transactions on Industry Applications,2009,45(4):1484-1490.

[7] 刘云,蒋卫平,印永华,等.高压交直流大电网的数模混合实时仿真系统建模[J].力系统自动化,2008,32(12):52-56.

LIU Yun, JIANG Weiping, YIN Yonghua, et al.Modeling of analogue-digital hybrid real-time simulation system applied in the UHV AC/DC great power grid[J].Automation of Electric Power Systems,2008,32(12):52-56.

[8] 陈磊,闵勇,叶骏,等.数字物理混合仿真系统的建模及理论分析[J].电力系统自动化,2009,33(23):9-13.

CHEN Lei,MIN Yong,YE Jun, et al. Modeling and theoretical analysis of Hardware-in-the-loop Simulation[J]. Automation of Electric Power Systems,2009,33(23):9-13.

[9] DMITRIEV-ZDOROV V B. Generalized coupling as a way to improve the convergence in relaxation-based sovers[J].Proc.Euro Daceuro VHDL,1996,16(20):15-20.

(责任编辑 侯世春)

Analysis of power hardware-in-the-loop simulation system interface characteristics

ZHOU Yanhua1, NIE Bingqing2

(1.College of Electrical Engineering, Northeast Dianli University,Jilin 132012,China; 2.Guodian Nanjing Automation CO,Ltd., Nanjing 211100, China)

The closed-loop stability and the simulation accuracy are two paramount issues in power hardware-in-the-loop (HIL) simulation. In order to solve the issues, the stability analysis and accuracy evaluation based on system transfer function were proposed. Five different interface algorithms were described, and their respective characteristics with respect to the system stability were compared. Through Matlab/Simulink simulations, the models of simple circuit digital simulation subsystem and physical tested system were established to simulate the stability and accuracy of the five interface algorithms offline. The results show the feasibility of damping and impedance method is higher than that of others in specific application.

power hardware-in-the-loop(HIL) simulation; interface algorithm; stability; accuracy

2015-06-23。

周艳华(1989—)，女，硕士研究生，研究方向为电力系统仿真。

TM743

A

2095-6843(2016)01-0028-06