一种配电网单体项目投资效益评价方法研究

刘胜利，高 英，姜金虹

(国网浙江平湖市供电公司，浙江 嘉兴 314200)



一种配电网单体项目投资效益评价方法研究

刘胜利，高 英，姜金虹

(国网浙江平湖市供电公司，浙江 嘉兴 314200)

目前配电网评价体系的研究主要着重于规划成效、综合评价、可靠性等全网或整体评价方面的内容，缺乏对单体项目投资效益评价方法的研究，项目的可行性研究报告也缺乏对投资效益的论证。介绍了针对上述问题，从安全性、可靠性、经济性等方面建立的一种35 kV及以下配电网单体项目投资效益评价方法。

配电网；单体项目；投资效益评价

随着经济和社会的发展，电力的需求不断提高，近年来，35 kV及以下配电网建设与改造需求规模持续上升, 而用于配电网建设与改造的投资有限，需要充分利用每一分投资，使其产生效益最大化。如何科学评价单体项目投资效益，合理安排投资项目，注重投入产出效益，避免低效、无效投资，成为供电企业亟待深入研究和解决的问题。传统的配电网项目的可行性研究报告仅侧重于项目的必要性与可行性的论证，缺乏对项目的投资效益的论证；目前有较多文献对配网评价模型或体系进行研究，文献[1-3]研究了配电网综合评价体系、模型；而针对研究配电网投资效益评价与决策模型方面的文献较少，文献[4] 研究了配电网规划评价指标体系和综合评价模型；文献[5-11]研究了电网安全性评估、经济性运行、协调性评估、可靠性评估等方面的问题；文献[12]针对35 kV和110 kV这两个电压等级配电网投资从项目效益和管理效益两个方面构建配网投资效益评价指标和体系，但只能用于配电网投资效益的后评价且主要针对高压配电网；文献[13-15]对电网投资决策、经济性、外部效益等方面做了一定研究，但缺乏单体配网项目投资效益的评价。以上文献主要着重于规划成效、综合评价、可靠性等全网或整体评价方面的内容，缺乏对单体项目投资效益评价方法的研究。本文针对上述问题，从安全性、可靠性、经济性等方面建立一种科学的、合理的、实用的、量化的35 kV及以下配电网单体项目投资效益评价方法。该方法包括单体项目投资效益评价新指标，计算单体项目各指标得分的评分函数，计算单体项目投资效益得分的公式，单体项目投资效益评价得分的标准分。运用该方法对历史年单体项目进行后评价；对在建或拟建的年度配电网总体投资效益和单体项目投资效益进行预测，根据投资效益评价得分高低判断各单体项目投资效益优良，安排单体项目投资优先顺序。

1 评价方法构架

配电网单体项目投资效益评价方法包括三部分内容：

(1)指标体系与权重。科学合理的指标体系与权重是投资效益评价的基础和评价目标的具体化实现。合理选取指标，保证指标体系的完整性与指标间的相互独立性，同时对每个指标进行详细定义并给出计算方法[1]。

(2)各指标得分的评分函数。用于计算某一单体项目各指标投资效益得分。

(3)单体项目投资效益的综合得分计算公式与标准分。其中综合得分计算公式用于计算某一单体项目投资效益各指标综合得分；标准分为配电网单体项目投资综合得分的基准分，用于衡量某一单体项目投资效益得分是否达标以及与标准分的差距。

2 指标体系

在构建指标体系时按照系统、科学和实用的原则选择考核指标，使其能够全面、准确、有效地反映配电网运行的主要状态和实际情况。

配电网规划是配电网年度投资建设计划的依据，为了实现投资效益的最大化，需要对配电网规划的科学合理性进行检验，因此对配电网规划成效进行评价就成为了配电网投资效益评价的重要内容之一。此外，从供电公司经营管理的角度来讲，投资计划和投资效益也是重点关注的内容。本文构建评价指标体系根据上述内容，紧紧围绕配电网投资效益这一核心评价目标，多方面收集资料作为指标源，并梳理出相应的评价指标。参照层次分析方法建立初步的评价指标体系，通过配电网项目关联性分析、专家打分等方式构建出指标体系。最后选取得分较高的指标作为最终评价指标,共选取19个二级指标，如表1所示。

表1 指标体系

3 指标权重

指标权重的设定是投资效益评价模型中的重要环节。赋权方法有主客观之分，常见权重计算方法有德尔菲法、层次分析法、变异系数法、熵权法、人工神经网络等。

德尔菲法与层次分析法同属于主观赋权方法，变异系数法、熵权法、人工神经网络等方法属于客观赋权方法。虽然客观方法能够最小限度地减少人为因素的干预，但是无法获得统一的权重标准，因此必须采用主观性的赋权方法。德尔菲法具有直观的特点，宜实际操作，与层次分析法相比较，更适合电网企业投资效益指标的权重确定。本文采用德尔菲法来设定指标权重。最终确定标层的规划成效、投资计划和投资效益，分别赋权值为0.3、0.3和0.4。指标权重值如表2所示。

表2 指标权重

4 指标评分函数

通过分数可以直观比较不同配电网的优劣，简单地采用五分位法来进行衡量不够科学。指标评分函数的归一化方法有最大值法、差值法、模糊数学法等，各种方法归一化计算结果一般不影响评价结论，都满足要求，本文综合采用以上方法。其基本步骤是：

(1)确定各指标的隶属度函数类型。隶属度函数可以是线性的，也可以是非线性的，视指标数据的分布情况来拟合。因为单位电网投资额与其投资效果评分关系可用多种函数表示，为得到两个变量间的最优函数，可使用线性(Linear)、二次函数(Quadratic)、三次函数(Cubic)、对数函数(Logarithmic)、指数函数(Exponential)、S 函数、幂函数(Power)等函数形式对其之间的关系进行拟合。

这些函数的拟合程度都较高，其中以三次函数的拟合程度最高。二次函数与三次函数的拟合程度相近，随着配电网建设发展的深入，很多指标值的改进将会越来越困难，或者每一点的改进所需要的投入将更多，因此评价判据应能体现出这一特点(线性函数不能体现这一特点)，同时为计算方便并考虑实际曲线的可能趋势，最终采用二次函数作为该电网现阶段电量需求与电网投资总额的关系函数。即有：

y=ax2+bx+c

(1)

式中x——指标值；

y——分数；

a,b——二次、一次项系数；

c——随机误差项。

(2)确定各评分函数的二次函数曲线。先设定各指标最大值对应的评分为100分(逆向指标为0分)，标准值对应的评分为70分，最小值对应的评分为0分(逆向指标为100分)。再研究出各指标的最大值、标准值、最小值。由以上3个坐标点即可确定评分函数的二次函数曲线。

由于单体项目投资效益评价指标为本文首次提出，无成熟的应用经验，故采用矩阵可分析法得出各个指标的最大值、标准值、最小值。矩阵为：

(2)

式中xij——第i个对象的第j个指标的数值。

按式(2)计算历史年配电网总体投资和单体项目投资效益评价指标数值，剔除不合理数据后，按数值大小把数据分成若干组，统计数据落入各组的频数，根据频数确定指标的标准值、最大值、最小值。由于篇幅有限，本文只列出部分指标的标准值、最大值、最小值，如表3所示。

表3 指标值

由以上3个坐标点确定各评分函数的二次函数曲线。由于篇幅有限，本文只列出部分指标评分函数，如表4所示。

表4 部分指标评分函数

5 投资效益综合评分

根据表4给出的评分函数可以计算出评价对象的指标得分，然后根据层次分析法向上计算得到某单体项目投资效益评价得分，式为：

(3)

式中Yj——指标的评分；

Wj——该指标权重。

6 投资效益评价标准分

6.1 理论依据

按式(3)计算出某单体项目投资效益综合评分结果后，对该项目投资投资效益水平有了直观的认识，但却很难得知该水平与标准投资效益的差异，因此投资效益评价标准分的研究具有重要意义。

标准分的研究，按照统计学中的正态分布曲线、标准差、六西格玛理论来实现。该理论简要介绍如下。

6.1.1 正态分布曲线

正态分布(Normal distribution)又名高斯分布(Gaussian distribution)，是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。若随机变量x服从一个数学期望为μ、方差为σ2的高斯分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。因其曲线呈钟形，因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ=0,σ=1的正态分布。正态分布曲线如图1所示：

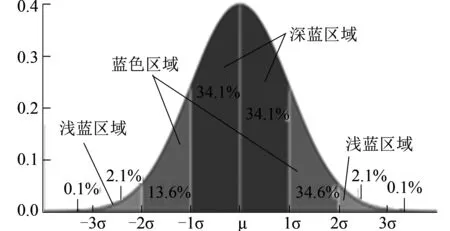
图1 正态分布图

深蓝区域是距平均值小于一个标准差之内的数值范围。在正态分布中，此范围所占比率为全部数值之 68.26%。根据正态分布，两个标准差之内(深蓝，蓝)的比率为 95.45%。根据正态分布，正负3个标准差之内(深蓝，蓝，浅蓝)的比率为 99.73%。

6.1.2 标准差和六西格玛

一组数据中，所有数减去其平均值的平方和，所得结果除以该组数的个数(或个数减一，即变异数)，再把所得值开根号，最后所得值就是这组数据的标准差。计算标准差的作用：

(1)表示变量分布的离散程度。标准差小，说明变量较多地分布在平均数的附近，比较密集。

(2)概括估计变量的次数分布，即各类观测值在总体中所占比例。

(3)估计平均数的标准误差。

(4)进行平均数的区间估计和变异系数的计算。

在描述一组数据资料时，集中量常用x表示，变异量常用S表示，样本观察值分布如下：

(1)在x±1S的范围内，观察值个数约占全部总数的68.26%。

(2)在x±2S的范围内，观察值约占总数的95.45%。

(3)在x±3S的范围内，观察值约占99.73%。

全距近似等于6倍标准差，可用(全距/6)粗略估计标准差。

6.2 标准分

在研究单体项目投资效益评价标准分时，利用标准差、正态分布曲线的性质，把占68.26%的基区作为主体。对国网平湖市供电公司历年131个配电网单体项目投资效益评价综合得分进行研究，最高分MAX(x)为63.5，最低分MIN(x)为17.1，其它结果如下：

全距：R=MAX(x)- MIN(x)=63.5-17.1(分)。

标准差：S=R/6=7.7(分)。

平均分：Savg=30.8(分)。

集中量x±1S的范围为30.8±.7，即23.1～38.5。根据正态分布曲线性质，分值在23.1～38.5之间占比为68.26%，所以，将单体项目投资效益评价标准分为23.1分。

7 算列

以国网浙江平湖市供电公司2015年配电网项目为算列，各单体项目投资效益评价得分如表5所示。表5中各单体项目顺序为按评价得分高低排列，最高分为56.7分，最低分为17.2分。有9个项目分数低于标准分23.1分，说明这9个项目投资效益未达到标准，可以考虑不安排实施或暂缓。另外22个项目分数高于标准分23.1分，说明投资效益达到标准，可根据得分高低顺序排定项目年度实施优先顺序，也可为年底申报增减投资项目提供依据。

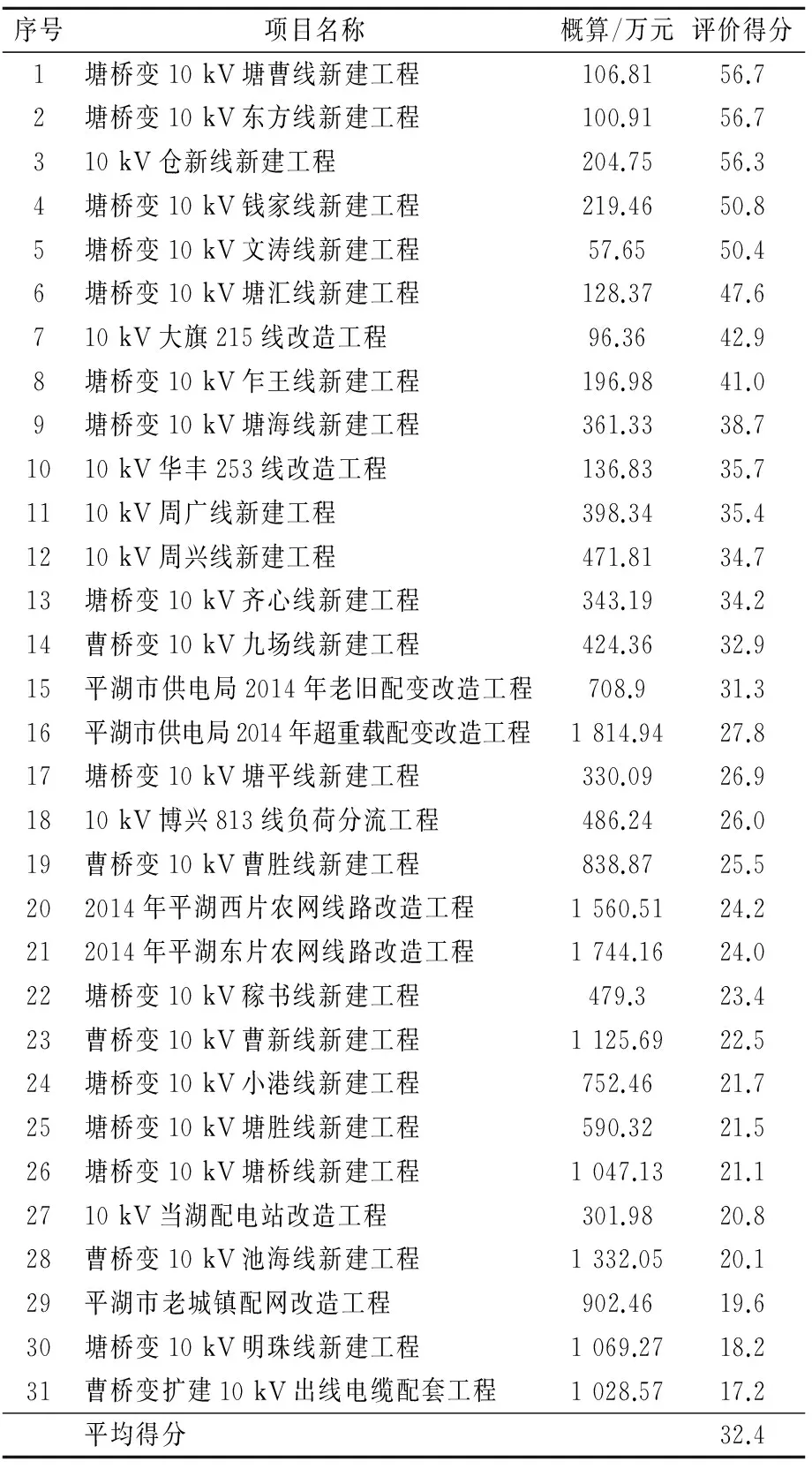
表5 2015年各单体项目投资效益评价得分

8 结语

本文从安全性、可靠性、经济性等方面建立一种科学的、合理的、实用的、量化的35 kV及以下配电网单体项目投资效益评价方法。提出19项用于评价单体项目投资效益的新指标，研究出计算单体项目各指标得分的评分函数，首次提出单体项目投资效益的得分公式，研究出单体项目投资效益评价得分的标准分。根据投资效益评价得分高低判断各单体项目投资效益优良，安排单体项目投资优先顺序。实例验证，该方法科学实用性，对建立配电网单体项目投资效益评价体系和以投资效益为导向的投资决策工作体系有重要意义。

[1] 韩震焘, 黄志伟, 葛少云, 等. 城市配电网综合评价体系[J]. 电网技术, 2012, 36(8): 95-99.

HAN Zhen-tao, HUANG Zhi-wei, GE Shao-yun, et al. A comprehensive evaluation system of urban distribution network[J]. Power System Technology, 2012, 36(8): 95-99.

[2] 肖 峻, 崔艳妍, 王建民, 等. 配电网规划的综合评价指标体系与方法[J]. 电力系统自动化, 2008, 32(15): 36-40.

XIAO Jun, CUI Yan-yan, WANG Jian-min, et al. A hierarchical performance assessment method on the distribution network planning[J]. Automation of Electric Power Systems, 2008, 32(15): 36-40.

[3] 王 琬, 刘宗岐, 曾 博, 等. 大都市电网综合指标体系与评价模型[J]. 现代电力, 2011, 28(4): 24-28.

WANG Wan, LIU Zong-qi, ZENG Bo, et al. Comprehensive index system and evaluation model of power grid for metropolitan cities[J]. Modern Electric Power, 2011, 28(4): 24-28.

[4] 羌丁建, 寿 挺, 朱铁铭, 等. 高压配电网规划评价指标体系与综合评价模型[J]. 电力系统保护与控制, 2013, 41(21): 52-57.

QIANG Ding-jian, SHOU Ting, ZHU Tie-ming, et al. An evaluation index system and comprehensive evaluation model on high-voltage distribution network planning [J]. System Protection and Control, 2013, 41(21): 52-57.

[5] 刘若溪, 张建华, 吴迪. 基于风险理论的配电网静态安全性评估指标研究[J]. 电力系统保护与控制, 2011, 39(15): 89-95.

LIU Ruo-xi, ZHANG jian-hua, WU Di. Research on static security index of distribution network based on risk theory[J]. System Protection and Control, 2011, 39(15): 89-95.

[6] 马丽叶, 卢志刚, 常 磊, 等. 基于灰色关联度的输电网经济运行指标体系研究[J]. 电力系统保护与控制, 2011, 39(12): 22-26.

MA Li-ye, LU Zhi-gang, CHANG Lei, et al. Study of index system of economic operation of grid based on gray correlation degree[J]. Power System Protection and Control, 2011, 39( 12): 22-26.

[7] 李金超, 牛东晓, 李金颖, 等. 基于GRA 与PCA 的电网发展协调性评估研究[J]. 电力系统保护与控制, 2010, 38(18): 49-53.

LI Jin-chao, NIU Dong-xiao, LI Jin-ying, et al. Evaluation of the power grid development coordination based on the GRA and PCA method[J]. Power System Protection and Control, 2010, 38(18): 49-53.

[8] 刘书铭, 李琼林, 陈栋新, 等. 中高压配电网非线性用户的电能质量特性研究[J]. 电力系统保护与控制, 2012, 40(15): 150-155.

LIU Shu-ming, LI Qiong-lin, CHEN Dong-xin, et al. Study of power quality characteristics of nonlinear electric user in medium-high voltage distribution networks[J]. Power System Protection and Control, 2012, 40(15): 150-155.

[9] 李晓辉, 徐 晶, 李 达, 等. 基于层次分析的配电网可靠性评估指标体系[J]. 电力系统及其自动化学报, 2009, 21(3): 69-74.

LI Xiao-hui, XU Jing, LI Da, et al. Index system of reliability evaluation for distribution network based on analytic hierarchy process[J]. Proceedings of the CSU-EPSA, 2009, 21(3): 69-74.

[10] 王成山, 王赛一, 葛少云, 等. 中压配电网不同接线模式经济性和可靠性分析[J]. 电力系统自动化, 2002, 26(24): 34-39.

WANG Cheng-shan, WANG Sai-yi, GE Shao-yun, et al. Economy and reliability analysis of different connection modes in MV distribution systems[J]. Automation of Electric Power Systems, 2002, 26(24): 34-39.

[11] 张功林, 林 韩, 温步瀛, 等. 中压配网主干线可靠性与经济性评估[J]. 华东电力, 2009, 37(8): 1355-1360.

ZHANG Gong-lin, LIN Han, WEN Bu-ying, et al. Evaluation of the reliability and economy of the main lines of middle voltage power distributing network[J]. East China Electric Power, 2009, 37( 8): 1355-1360.

[12]李 娟, 李晓辉, 刘树勇, 等. 基于理想解法和灰色关联度的配电网投资效益评价[J]. 华东电力, 2012, 40(1): 0013-0017.

LI Juan, LI Xiao-hui, LIU Shu-yong, et al. Investment Benefit Evaluation for Distribution Network Based on TOPSIS and Grey Correlation Degree [J]. East China Electric Power, 2012, 40(1): 0013-0017.

[13]田 廓, 张怡, 王尔康, 等. 电网建设项目投资决策评价研究[J]. 华东电力, 2009, 37(10): 1623-1626.

TIAN Kuo, ZHANG Yi, WANG Er-kang, et al. Evaluation of investment portfolio for grid projects[J]. East China Electric Power, 2009, 37(10) : 1623-1626.

[14]闫庆友, 颉 超. 基于实物期权的电网项目投资决策经济性评价[J].水电能源科学, 2010, 28(10): 145-147.

YAN Qing-you, XIE Chao. Study on Economic Evaluation for grid investment based on real option method[J]. Water Resources and Power, 2010, 28( 10) : 145-147.

[15]董 军, 蒋 雪. 计及外部效益的城市配电网项目评价研究[J]. 华北电力大学学报, 2010, 37(5): 62-67.

DONG Jun, JIANG Xue. Comprehensive assessment of urban distribution network expansion considering externality[J]. Journal of North China Electric Power University, 2010, 37( 5): 62-67.

(本文编辑：严 加)

Evaluation Method for Distribution Network Single Project Investment Effectiveness

LIU Sheng-li, GAO Ying, JIANG Jin-hong

(State Grid Zhejiang Pinghu Power Supply Company, Jiaxing 314200, China)

Currently, the research on the distribution network evaluation system pays attention to the whole or overall grid evaluation content such as planning effectiveness, comprehensive evaluation, reliability, etc. The research on single project investment effectiveness evaluation method is insuffiecient. The Project feasibility study reports also fail to demonstrate the project investment efficiency. Therefore, this paper establishes an investment effectiveness evaluation model for 35kV or below distribution network single project considering the safety, reliability and economic efficiency.

distribution network; single project; investment effectiveness evaluation

10.11973/dlyny201605004

刘胜利(1981)，男，工程师，研究方向为电力系统规划设计、电网项目投资分析。

TM715

B

2095-1256(2016)05-0548-06

2016-03-17