实数序列的通项公式问题

东洪平

(陇南师范高等专科学校数学系,甘肃成县 742500)



实数序列的通项公式问题

东洪平

(陇南师范高等专科学校数学系,甘肃成县 742500)

讨论实数序列的通项公式，证明了任意实数序列可以通过[0,+∞)上任意次连续可微函数给出其通项公式，任意单调有界实数序列可以通过(-∞,+∞)上的解析函数给出其通项公式.

实数序列；单调有界数列；通项公式

0 引言

在中学数学中，常常给定一个数列所满足的关系式，要求写出该数列的通项公式.受这类问题的启发，本文提出一个更加一般性的问题：

要回答这个问题，我们首先需要澄清一些基本概念.

定义1 一个数列l是指定义在一个可数有序集S上的一个实值函数f(n)(n∈S)，很多情况下这个有序集合就取自然数集的一个子集[1-2].

不失一般性，不妨取

(1)

能否给出函数f的表达式？这样一来问题似乎又显得有点平凡，因为理论上(1)式本身就可以看成是函数f的一个表达式，但是如果将函数f限定在某个特定的函数类中，问题就有点不平凡了.事实上，回答这个看似简单的问题，其难度远远超出我们的预料.本文将紧紧围绕这一问题进行深入探讨.

1 主要结果

在一个特定的函数类中寻找给定数列的通项公式，其更为严格的数学描述如下：

解答问题2的关键在于函数族F的选取.

1.1 连续函数族和连续可微函数族的情形

先在连续函数族中考虑这一问题，此时可取F=C[0,+∞)，我们有

证明 只考虑N=+∞，即l是无穷数列的情形.为方便起见，补充a0=0，定义函数

(2)

n=0,1,2,…，则f(x)即为所求.

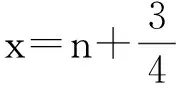
由此可知f在(2)式中区间的每一个端点处连续，从而f∈F.易见f(n)=an(1≤n<+∞). 】

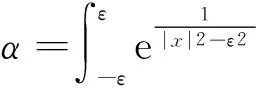
设f(x)是由(2)式所定义的函数，对x<0，补充定义f(x)=0，则f(x)是(-∞,+∞)上的连续函数.令

我们证明g(x)即为所求.

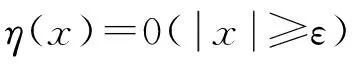
(3)

所以对任意有界区间I=[a,b]，当x∈I时，我们有

(4)

(4)式左端作为含参量x的积分关于x∈I一致收敛，由数学分析知识[3-4]可知,g在I上任意次连续可微，再由I的任意性可知，g是(-∞,+∞)上任意次连续可微的函数.

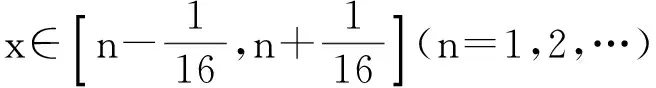
注意到

则由上式和函数f(x)的定义，我们有

特别地，g(n)=an,所以g满足要求. 】

注1:定理2的证明用到了偏微分方程理论中经典的“磨光技术”[5].

1.2 解析函数族的情形

若N<+∞，即l是有穷数列，则上述问题的回答是肯定的，此时令

则f(x)为多项式，且

从而f(x)给出了数列的通项公式.

但当N=+∞时，问题要困难得多，我们至今没有一般性的结论.不过对于单调数列，我们仍然获得了一个有意思的结果.

类似可定义单调递增数列.

数列l称为单调递减的，若存在[0,+∞)上的连续函数f(x)使得f(n)=an，且

(5)

另一方面，若函数f(x)满足条件(5)，则很容易构造[0,+∞)上一个新的单调递减的连续函数g(x)使得g(n)=f(n)(1≤n≤N)，因此数列l的单调性又可以直接用单调函数来定义.

定义3 数列l称为单调递减的，若存在[0,+∞)上的单调递减的连续函数g(x)，使得g(n)=an(1≤n≤N).

我们从函数sinπx的幂级数表示

(6)

入手.由Euler对正弦函数的无穷乘积表示[6-7]，有

从而

(7)

上式右边的无穷乘积在[0,+∞)上是收敛的，且

(8)

令

(9)

则

此外，我们有

将(6)式代入(9)式，有

(10)

将(10)式右边的无穷乘积展开，可得

(11)

其中

(12)

分别比较(7)和(10)式以及(8)和(12)式可知，(10)和(11)式右边在[0,+∞)上均收敛.令

(13)

则

交换求和符号，可得

其中

(14)

下面考虑(13)到(14)式中运算的合理性问题，为此只需说明其中级数的收敛性即可.

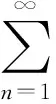
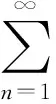
在每一个整数点x=n处，有

故f(x)即为所求.

(ii) 一般情形.

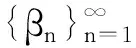
注2:定理3的一个等价陈述是：设g(x)是[0,+∞)上的单调有界连续函数，则存在一个(-∞,+∞)上的解析函数f(x)满足f(n)=g(n),n=1,2,….

注3:就中学数学而言，自然是期望能够在初等函数族F中给出问题2的一个回答.对此，目前我们似乎还看不到希望.

致谢：作者衷心感谢审稿人仔细审阅了该文初稿并提出了大量宝贵的修改意见,正是这些意见帮助我们大大提高了论文质量，并激发我们改进了关于单调数列的相关结果.本文在写作过程中，也曾得到天津大学理学院博士生导师李德生教授的指导，在此一并表示感谢！

[1]DWARDGE.Introduction to Analysis[M].NewYork：AmericanMathematicalSociety,2009.

[2] JAMES R M.Topology:AFirstCourse[M].Upper Saddle River,New Jesey:Prentice-Hall,Englewood Cliffs,1975.

[3] 陈传璋，金福临，朱学炎，等.数学分析[M].北京：高等教育出版社，1983.

[4] 伍胜健.数学分析[M].北京：北京大学出版社，2010.

[5] EVANS L C.PartialDifferentialEquations[M].New York:American Mathematical Society,1998.

[6] EBERLEIN W F.On Euler’s infinite product for the sine[J].JMathAnalAppl,1977,58(1):147.

[7] KANOVEI V G.The correctness of Euler’s method for the factorization of the sine function into an infinite product[J].RussMathSurv,1988,43(4):65.

(责任编辑 马宇鸿)

On the formulas of general terms of real sequences

DONG Hong-ping

(Department of Mathematics，Longnan Teachers College，Chengxian 742500,Gansu,China)

This paper is concerned with the formulas of general terms of sequences of real numbers.It is proved that for any sequence of real numbers,the formula of general terms of the sequence can be given via continuously differentiable functions on [0,+∞),and for any bounded monotone sequence of real numbers,its general term formula can be obtained by using analytic functions on (-∞,+∞).

sequence of real numbers；monotonically bounded sequence;formulas of general terms

10.16783/j.cnki.nwnuz.2016.01.004

2014-12-06;修改稿收到日期:2015-06-17

东洪平(1963—)，男，甘肃成县人，副教授.主要研究方向为数学分析.

E-mail:donghongping@163.com

O 174.1

A

1001-988Ⅹ(2016)01-0017-04