基于M-V法、Wahl法和有限元法的汽轮机隔板的强度对比分析

杨光辉， 陈庆波

(北京科技大学机械工程学院，北京 100083)

基于M-V法、Wahl法和有限元法的汽轮机隔板的强度对比分析

杨光辉， 陈庆波

(北京科技大学机械工程学院，北京 100083)

长期处于高温高压的汽轮机隔板只有在一定强度和刚度下，才能安全进行生产工作。分别基于经典算法Wahl法、M-V法和有限元法，对某亚临界状态机组隔板进行强度分析和对比。结果表明，隔板最大应力在靠近中分面叶片的进气叶根处，最大应变在中分面内径内环处，板体最大应力在垂直于中分面的内环内径处，其中有限元法和 Wahl法误差较小，验证了有限元方法的可行性。

汽轮机隔板；有限元；Wahl法；强度分析

隔板用于固定静叶片和防止汽轮机各个级间漏气，所以在汽轮机中起着至关重要的作用。随着大容量、高参数的汽轮机组被广泛地使用，高压缸中的隔板处于非常恶劣的环境下，不仅有高温还有很高的压力差，使隔板会产生一定的挠度。隔板挠度最大的地方在中分面靠近内径处，如果隔板没有足够的强度和刚度，那么由正常工作产生的挠度会大于动静叶之间的间隙，这样动静隔板相碰便会发生非常大的事故。因此，合理正确地分析隔板的应力和挠度对汽轮机隔板的安全工作起着重要的作用。基于大型有限元软件ANSYS Workbench 15.0对隔板进行有限元分析，并将其与经典算法——Wahl法和M-V法进行了比较，验证了有限元法对高压隔板计算的可行性。

1 M-V法

M-V法又称 Sm ith法，是最早采用的隔板计算方法，首先被英国M-V透平制造厂用于计算隔板强度。其对于隔板计算作了如下假定[1]：

(1) 隔板外缘固定在完全刚性的支座上；

(2) 隔板上承受均匀分布的蒸汽载荷；

(3) 支反力沿支承周边分布依照正弦曲线规律(与实际情况不符)；

(4) 在计算隔板本身的应力和挠度时，假定静叶绝对刚性；在计算静叶应力和挠度时，假设隔板外缘和板体是绝对刚性的；

(5) 隔板受力后隔板的径向截面形状保持不变；

(6) 不考虑隔板本身的曲率，即计算时对于力和变形的关系利用直梁公式。

隔板体最大应力，在垂直于隔板中分面的内径处，其值为

隔板体最大挠度，在隔板中分面内径处，其值为

式中，Δp为隔板两侧最大压差；D为气缸内径；S为隔板体厚度；J为隔板的计算惯性矩；E为工作温度下隔板材料的弹性模量；Kσ为应力计算系数；KD为挠度计算系数。

该方法还可以计算静叶中的最大应力和最大挠度(此时假定隔板体为绝对刚性)，其公式如下：

静叶片的最大挠度为

静叶片最大应力为

式中，Dm为静叶平均直径(m)；Dg为汽封处内径；l为静叶高度(m)；Z为静叶数；E为静叶材料工作温度时弹性模量(MPa)；I为静叶横截面对X-X轴的惯性矩(m4)；W为静叶截面对X-X轴的截面系数(m3)，W=I/e，其中e为离中性轴X-X最边缘的距离。

则在靠近隔板中分面汽封内径处的最大挠度的计算公式由fmax和两部分组成

已知Δp=0.92 MPa，D=1.708 m，Dm=1.369 m，Dg=0.750 m ， l=0.170 m ， S=0.119 m ，J=5.673368×10–5m4，由以上公式可以求得

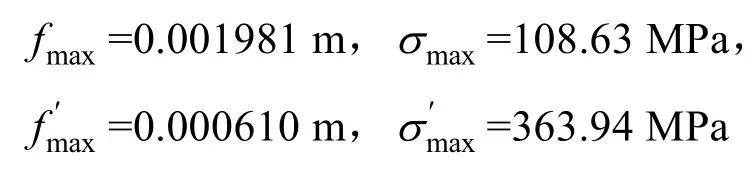
隔板体最大挠度为

隔板体最大应力为σmax=108.63 MPa。

2 Wahl法

与M-V法相比，Wahl法基于更加严格的理论前提。其不考虑静叶的存在，把隔板当作一整块半圆环，利用曲梁斜弯曲理论的近似解法，得到隔板的受力状态。由于高压级隔板的静叶往往比较短，因此Wahl法对计算静叶较短的高压隔板的计算与实际情况比较吻合，但是其缺点就是无法计算叶片的最大应力。Wahl提出在隔板的内、外径差别不是特别大时，即 d/ D0≥ 0.4，隔板在受力后其径向截面不发生变形[2]。

在中心截面r=r0处，隔板的挠度最大，此处的最大挠度为

式中，c1、c2、λ1、λ2为待求系数；r0为气缸内环的内半径；r=r0+a； a=(R -r0)/2；R为外环的外半径；；a1=2e-a； e=(r1-r0)/2；r1=r+a；Jx为截面对O1x轴的惯性矩；E为弹性模量；；C为隔板的扭转刚度； B =2eΔ p( r+ e) + q0r0；；

其中：Δp为压差；q0和m0为汽封处转化而来的均布载荷和均布力矩。

最大弯应力发生在隔板内环垂直于中分面的靠近内径的位置

式中

其中，S为隔板的厚度；K为应力沿径向截面分布不均匀的系数；J为截面对O1x轴的惯性矩。

由以上公式可以求得：

隔板体最大挠度为Δ=1.21 mm；

隔板体最大应力为σmax=14.8 MPa。

3 有限元法

3.1 模型的建立

某汽轮机厂的亚临界状态气缸，机组的额定蒸汽压力为16.67 MPa，主蒸汽温度为538 ℃，隔板的参数设为：外环外径为1 838 mm，外环内径为1 518 mm，内环外径为1 220 mm，内环内径为795 mm，静叶高度为 170 mm，静叶最大宽度为32 mm，静叶数量为46片。

在ANSYS Workbench 15.0建立了一个静力学分析项目，将 SolidWorks建立的模型导入到DM(DesignModeler)模块中，定义材料的属性如下：①静叶叶片及焊接块：弹性模量为1.607×105MPa，泊松比为 0.3；②隔板内外圈：弹性模量为1.696×105MPa，泊松比为0.3。如图1所示，对模型进行网格划分，内外环以及焊接块由于形状比较简单，采用扫略的方式，静叶部分采用四面体单元进行划分，节点数为423 638，单元数为127 499。

图1 隔板网格划分模型

3.2 位移边界条件设定

图2为隔板的边界条件示意图，图中向右为x正方向，向上为y正方向，垂直xy平面向外方向为z正方向。由于隔板的外缘支承在气缸或隔板套的隔板槽中，所以轴向约束 uz=0；隔板外环由紧固螺栓联接固定在气缸或隔板套上，上下两半对称，则对称约束uy=0，不转动所以Ry=0；隔板顶部有定位键，防止隔板在蒸汽压力下移动旋转，所以外环环面ux=0[3]。

图2 隔板边界条件示意图

3.3 力的边界条件设定

汽轮机受力情况比较复杂，这是因汽轮机的工作原理所致，即隔板内环和外环受到前后压力差的作用。蒸汽通过喷嘴叶栅，蒸汽流速增大、流速方向改变，同时蒸汽对隔板静叶必然产生一定的反作用力。如图 3所示，由动量定理可知，单个静叶流道内蒸汽受到轴向、周向作用力分别为[4]

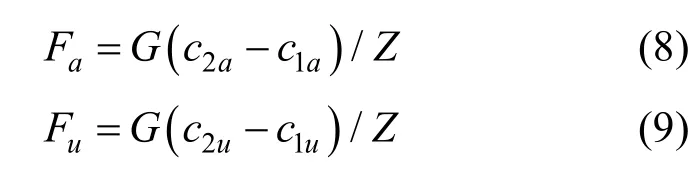
式中，c1为进气速度；c1a、c1u分别为c1的轴向、周向分量；c2为出气速度；c2a、c2u分别为c2的轴向、周向分量；Z为隔板叶片数；G为蒸汽流量。

在Ansys Workbench 15.0中采用Fluid Flow (CFX)进行流体分析，建立两个静叶喷嘴的流体模型，采用的是扫掠方式划分网格，其中共计68 000个节点，60 909个单元。图3所示模型的左右为叶片的内弧和背弧壁，上下为隔板内外环壁，前面为进气侧，后边为出气侧。

模型设定为稳态计算，求解方程为Navier-Stokrs方程，湍流模型选择k-ε模型。流体的进口条件设定为蒸汽流量10.63 kg/s，出口边界条件设定为蒸汽压力15.76 MPa，壁面为绝热无滑移条件[4]。

图3 静叶单通道计算模型

图 4所示为计算得到的流场压力分布云图，可以看出从进气侧到出气侧，随着静叶叶片弦长的增加蒸汽压力在不断的减小，在流场最后出口附近出现负压。进口压力约为16.64 MPa，出口压力约为15.72 MPa，进出口的蒸汽压差为0.92 MPa。

图4 流场压力分布云图

图 5所示为计算得到的流场速度矢量分布云图，可以看出进口速度的轴向分量差不多为零，只有轴向速度分量，随着静叶叶片弦长的增加，蒸汽的速度也在不断地增加。

图5 流场速度矢量图

由表1以及式(8)、(9)可以算出整个隔板的受力情况，其中隔板体内环和外环受到前后压差的压力，静叶片受到蒸汽气流的反作用力，具体数值见表2。

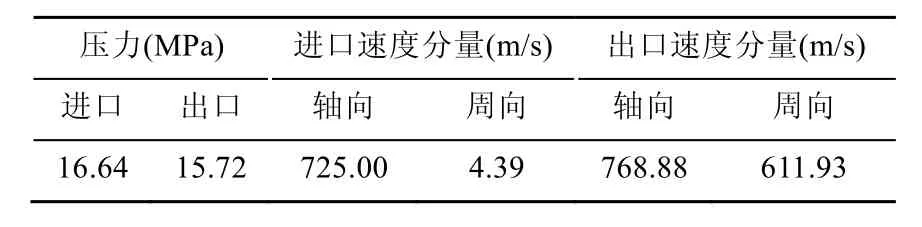
表1 流体计算结果

表2 隔板受力值

3.4 有限元法计算结果分析

由隔板应变云图(图6)可以看出，隔板中靠近中心截面叶片的叶根处受到的应力最大，且在进气一侧达到531.3 MPa，然而板体中应变最大的位置出现在与中心截面垂直的内环内径处(图7)；从隔板的应变云图(图8)可以看出，隔板的变形从外环到内环逐渐增大，最大挠度出现在中心截面的内环内径处，达到了1.07 mm。这一结果与Wahl法将隔板简化为悬臂梁的思想一致，隔板外环相当于悬臂梁的根部，承受着整个隔板的应力[5-8]。

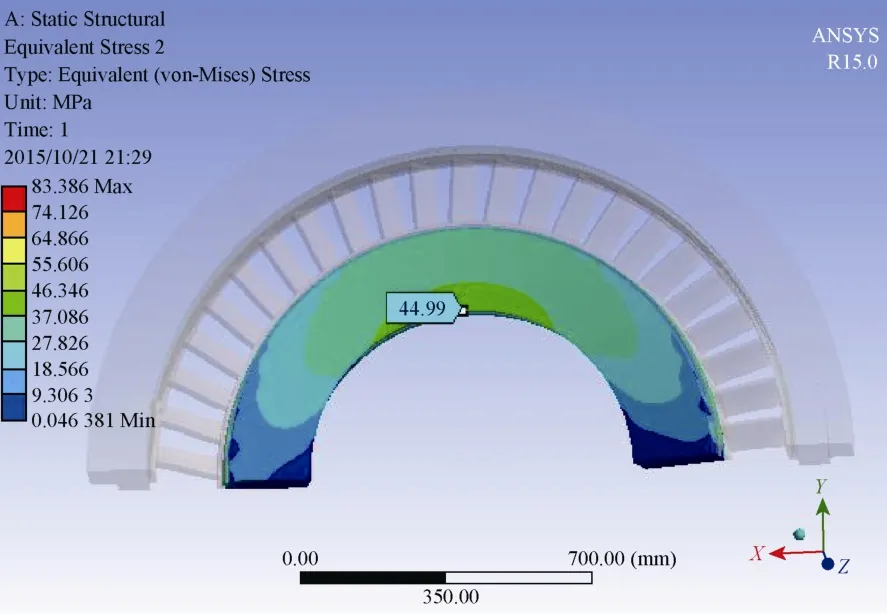
图7 隔板板体应力云图

图8 隔板整体应变云图

隔板的挠度大小对隔板的设计起着至关重要的作用，因为变形过大会使动静隔板发生摩擦、碰撞等事故，如果有静叶折断，那么断叶会随着蒸汽进入下一级隔板，从而造成整个汽轮机瘫痪的事故发生。由有限元云图显示可知，隔板体的最大应力和挠度位置与Wahl法计算最大应力挠度的位置大致符合，且有限元法进一步考虑了隔板的结构、受力以及位移约束，所以认为其结果更加接近真实性。表3为隔板挠度以及应力的3种计算结果的对比，表中数据显示，Wahl法相比M-V法具有更小的误差，表明Wahl可以在高压级隔板初级设计中采用。而M-V法最大挠度与有限元法相差太大，是因为M-V法适合静叶较长的隔板，隔板的最大挠度是板体挠度与静叶挠度相加[9]。

表3 有限元法与Wahl法、M-V法比较

4 结 论

M-V法最大挠度与有限元法相差太大，是因为M-V法适合静叶较长的隔板，隔板的最大挠度是板体挠度与静叶挠度相加。有限元法与Wahl法的隔板挠度相差不大，而且隔板体的最大应力和挠度位置与Wahl法计算最大应力挠度的位置大致符合，隔板最大应力位置在靠近中分面的叶片的叶根处，最大挠度在中分面内径处。

[1] 丁有宇. 汽轮机强度计算手册[M]. 北京: 中国电力出版社, 2010: 73-113.

[2] 吴厚钰. 透平零件结构和强度计算[M]. 北京: 机械工业出版社, 1982: 253-263.

[3] 周轶喆, 刘明军, 胡柳欣, 等. 汽轮机隔板的塑性变形分析[J]. 动力工程, 2009, 29(1): 46-48, 67.

[4] 董成龙. 大型汽轮机的隔板刚度特性研究[D]. 大连:大连理工大学, 2013.

[5] 刘 平. 典型隔板的强度刚度有限元分析[J]. 汽轮机技术, 2004, 46(5): 333-335.

[6] 马 骏, 赵海峰, 孙 伟, 等. 汽轮机隔板强度计算方法的比较[J]. 东方电气评论, 2015, 29(114): 29-32.

[7] Chen J P, Yang G H, Yang B. Finite element analysis of steam turbine diaphragm [J]. Computer Aided Drafting, Design and Manufacturing, 2014, 24(4): 60-63.

[8] Chen J P, Zhao W D, Cai W H, et al. Strength analysis of steam turbine diaphragm w ith a crack [J]. Computer Aided Drafting, Design and Manufacturing, 2015, 25(1): 52-55.

[9] 胡柳欣, 忻建华, 葛 诵, 等. 汽轮机隔板高温蠕变寿命评估方法的研究[J]. 动力工程, 2009, 29(3): 232-235.

Com parison Analysis of Intensity for the Turbine Diaphragm Based on Wahl, M-V and Finite Element Methods

Yang Guanghui, Chen Qingbo

(School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Steam turbine can remain a safe production state for a long period under the environment of high temperature and high pressure if it has certain good strength and intensity. The methods of Wahl, M-V and finite element analysis were used in analysis of intensity for a subcritical state turbine diaphragm. The results showed that the maximum stress of the diaphragm appeared at the blade’s enter side of the blade root, the maximum strain appeared at the equatorial plane at an inner diameter of the inner ring, and the maximum stress of the board appeared at the inner diameter of the inner ring which was vertical to the equatorial plane. The errors of finite element method and Wahl method were smaller, so it proved the reliability of finite elements analysis.

turbine diaphragm; finite elements analysis; Wahl method; intensity analysis

TK 263.2

10.11996/JG.j.2095-302X.2016040577

A

2095-302X(2016)04-0577-05

2015-11-01；定稿日期：2016-01-09

北京高等学校青年英才计划项目(YETP0369)；中央高校基本科研业务费项目(FRF-BR-15-047A)

杨光辉(1977–)，男，山东诸城人，副教授，博士。主要研究方向为机械装备行为及控制等。E-mail：yanggh@ustb.edu.cn