二维板材切割下料问题的一种确定性算法

曾兆敏， 王继红， 管卫利

(1. 四川信息职业技术学院，四川 广元 628017；2. 郑州科技学院电气工程学院，河南 郑州 450064；3. 南宁学院信息工程学院，广西 南宁 530200)

二维板材切割下料问题的一种确定性算法

曾兆敏1， 王继红2， 管卫利3

(1. 四川信息职业技术学院，四川 广元 628017；2. 郑州科技学院电气工程学院，河南 郑州 450064；3. 南宁学院信息工程学院，广西 南宁 530200)

研究二维板材切割下料问题，即使用最少板材切割出一定数量的若干种矩形件。提出一种结合背包算法和线性规划算法的确定性求解算法。首先构造生成均匀条带四块排样方式的背包算法；然后采用线性规划算法迭代调用上述背包算法，每次均根据生产成本最小原则改善目标函数并修正各种矩形件的当前价值，按照当前价值生成新的排样方式；最后选择最优的一组排样方式组成排样方案。采用基准测题，将该算法与著名的T型下料算法进行比较，实验结果表明，该算法比T型下料算法更能节省板材，计算时间能够满足实际应用需要。

二维切割；矩形件下料；背包算法；线性规划算法

板材二维切割下料(two dimensional cutting stock，TCS)问题是指用板材切割出一定数量的若干种矩形件，在每种矩形件的需求量得到满足的条件下使得所切割的板材张数最少。TCS问题是属于NP难的组合优化问题，在机械制造业领域有广泛的应用[1-3]。TCS问题的解称为排样方案，由一组排样方式组成，并且指出按照每种排样方式所切割的板材张数。排样方式是指单张板材上矩形件的排列方式。

目前文献中对排样方式生成算法研究较多，Hifi等[4]运用束搜索原理提出了两阶段排样方式的生成算法。Cui和Huang[5]提出了T型、两段[6]排样方式的启发式生成算法。Cui[7]及潘卫平等[8]分别提出了三阶段排样方式、匀质条带三块排样方式的背包算法。以上算法，只能解决单张板材上的矩形件无约束排样问题，无法解决下料问题。陈学松等[9]采用遗传模拟退火算法对下料问题进行了求解，但该算法生成的排样方案板材切割工艺复杂，且材料利用率较低。崔耀东[10]及Cui[11]提出了T型排样方式的递归算法，并将该算法和线性规划相结合构造了下料算法，使下料问题得到了较好地解决。本文提出一种新的均匀条带四块(four block uniform strips, FBUS)排样方式，首先构造生成该种排样方式的背包算法；然后采用线性规划算法迭代调用该背包算法求解排样方案。实验结果表明，本文算法能够有效地解决板材TCS问题。

1 基本概念

1.1 问题定义

TCS问题[1]：用规格为L(长)×W(宽)的板材切割出一定数量的m种矩形件，其中第i种矩形件的规格为 li×wi，个数为 bi；优化目标是用尽量少的板材切割出所需的全部矩形件。

板材二维无约束排样(two dimensional unconstrained packing, TUP)问题：将规格为L×W的板材切割成m种矩形件，其中第i种矩形件的规格为 li×wi，价值为 vi，对每种矩形件的个数无约束；优化目标是使得板材切割的矩形件总价值V最大。数学模型为

其中，pi为排样方式P中第i种矩形件的个数。

TCS问题的解(排样方案)由一组排样方式组成，每种排样方式由相应的TUP排样算法生成。经常采用线性规划(linear programm ing, LP)求解TCS问题。LP的求解步骤为：

步骤 1. 构造一个初始可行解。

步骤 2. 确定第 i种矩形件的当前价值，i= 1,2,…,m。

步骤 3. 采用相应的TUP算法求解模型(1)，得到一个新的排样方式P。

步骤 4. 用排样方式 P置换当前排样方案中的一个排样方式，当且仅当 P能改善当前排样方案，转步骤2；否则转步骤5。

步骤 5. 输出排样方案。

1.2 FBUS排样方式相关概念

1.2.1 条带

一个或多个矩形件排成一行(列)所占据的板材条称作条带[11]。有普通条带、同质条带、均匀条带3种类型，如图1所示，条带中的数字表示矩形件编号。普通条带可以切割成多种矩形件、同质条带只允许切割成一种矩形件、均匀条带可以切割成多种宽度相同的矩形件。文献中针对普通条带和同质条带研究较多，而均匀条带尚未见相关研究。由分析可知：①均匀条带可直接切割成矩形件而无需后续修剪，因此其切割工艺比普通条带简单。②均匀条带可排放多种矩形件，板材利用率高于同质条带。因此均匀条带能较好地平衡切割工艺与材料利用率。本文采用均匀条带。

图1 条带

1.2.2 FBUS排样方式

FBUS排样方式首先用一条父分界线将板材分成两个子板，然后用两条与父分界线垂直的子分界线将子板分成A、B、C、D 4个块，各块中只排放长度和方向均相同的均匀条带；当子板是左右排列时称之为X向FBUS排样方式，当子板是上下排列时称之为Y向FBUS排样方式(图2)。

图2 FBUS排样方式的2种类型

2 算法原理

2.1 排样方式生成算法

2.1.1 生成条带

令vi为第 i种矩形件的价值，s(j,x)为条带x(长)×wj(宽)的价值，ei为条带中第i种矩形件的数量，则有如下公式

2.1.2 生成块

块由条带组成，且同一块由长度和方向均相同的条带组成。将水平条带组成的块称为X向块，将竖直条带组成的块称为Y向块。对于X向块，条带的长度等于块的长度；对于 Y向块，条带的长度等于块的宽度(块的水平边为长，竖直边为宽)。对于块x(长)×y(宽)，记f( x, y)为块的价值，x≤L，y≤W。对X向块，设其由 zX(j, x)个水平条带 x×wj组成，fX(x, y)为块价值；对Y向块，设其由 zY(j, y)个竖直条带y×lj组成，fY(x, y)为块价值。则有如下数学模型

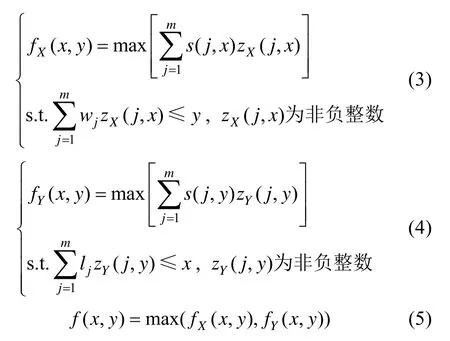
模型(3)、(4)均是无约束背包问题，具体解法可参阅文献[12]。

2.1.3 生成FBUS排样方式

设最优X向、最优Y向FBUS排样方式的价值分别为VX、VY，最终的FBUS排样方式价值为V。则有如下公式

式(6)中 x为父分界线的横坐标，y1，y2为两条子分界线的纵坐标。

式(7)中y为父分界线的纵坐标，x1，x2为两条子分界线的横坐标。

2.2 排样方案生成算法

采用LP求解排样方案[11]，其线性松弛模型为

其中，z为排样方案总共使用的板材面积；C= [c1, c2,···,cm]，其中ci=L×W(i=1,2,...,m)； X= [x, x,···,x ]T，其中x为第i种排样方式使用的数

1 2 mi量；A为排样方案矩阵(m阶方阵)，其元素aij表示第j种排样方式中包含第i种矩形件的个数；B= [b, b ,...,b]T，其中b为第i种矩形件的需求量。

1 2 mi本文排样方案生成算法有以下7个步骤(图3)：

步骤 1. 输入板材尺寸数据 L、W，毛坯尺寸和需求量数据 li、 wi、bi。

步骤 2. 令每张板材只排放一个第i种矩形件，得到初始可行排样方案，易知该排样方案使用张板材，此时A为单位矩阵。

步骤3. 确定矩形件价值向量 V=C A-1= [v1, v2,···,vm]。

步骤 4. 按照各矩形件当前价值，调用排样方式生成算法，生成一个新的排样方式 P= [p1,p2,···,pm]，pi表示该排样方式包含第i种矩形件的个数。

步骤 5. 计算引进 P是否能够减少当前排样方案所用板材总面积z。

步骤 6. 用P替换原有排样方案中的第k个排样方式，其中k满足生成一个新的排样方案，记录此时的排样方案矩阵A。

步骤7. 输出最终排样方案。

图3 排样方案生成算法的流程图

3 实例验证

在VS2012平台上进行本文算法实验编程。所用计算机为 AMD Athlon(tm) 64 X2 Dual Core Processor 4800+2.51 GHz，2.87 GB内存。由于本文算法是确定的，故只要算法执行完毕，实验条件对算法求得的解无影响。

3.1 本文算法与文献[7]算法比较

采用文献[7]的 15道随机测题，板材尺寸L、 W∈[2000,3000]，矩形件种数 m∈ [50,200]，尺寸li、wi∈[50,200]。文献[7]算法(TKP算法)生成三阶段排样方式，本文算法生成四块排样方式。令VTS、VFB分别为三阶段排样方式和四块排样方式价值，tTS、tFB分别为TKP算法和本文算法生成排样方式所耗费的计算时间。表 1为测题的数值实验结果。从表1可以看出，15道测题中本文算法排样价值有9道测题高于TKP算法，有4道测题等于TKP算法，有2道测题低于TKP算法。本文算法平均排样价值为4 391 592，TKP算法平均排样价值为4 389 562，本文算法平均排样价值高于TKP算法。对于15道测题本文算法平均计算时间与TKP算法近似，计算时间能够满足实际应用需要。

表1 15道测题的实验结果

3.2 本文算法与文献[11]算法比较

采用文献[11]的 6道测题(P1～P6)，板材尺寸L、 W∈[1500,2500]，矩形件种数 m∈ [2,18]，尺寸li、wi∈ [150,600]，需求量 bi∈ [1000,20000]，i= 1,2,· ··, m 。实验结果如表2所示，其中UT、UF、uT、uF分别为T型下料算法和本文下料算法排样方案耗费的板材张数和板材利用率。本文算法求解6道测题总共耗时0.71 s，平均每道测题耗时0.12 s，计算时间在实际应用中合理。从表2可以看出6道测题，T型下料算法平均耗费板材4 520张，利用率为97.14%；本文下料算法平均耗费板材4 492张，利用率为97.67%。本文下料算法比T型下料算法节省28张板材，提高材料利用率0.53%。另外注意到T型下料算法采用的是普通条带，本文下料算法采用的是均匀条带，由于均匀条带可直接切割成矩形件而无需后续修剪，故在切割工艺方面，本文下料算法优于T型下料算法。

图4为本文下料算法生成的测题3排样方案，此排样方案由 12种排样方式组成，其中“图 4(a)方式1(303张)”表示按照排样方式1使用板材303张。12种排样方式总共使用板材7 153张，板材利用率为97.38%。

表2 6道测题的实验结果

图4 测题3的排样方案

4 结 束 语

材料利用率和切割工艺复杂度是板材TCS问题需要考虑的 2个主要因素。本文提出了新型的FBUS排样方式，其将板材分为4个块，每个块中只排放方向相同的均匀条带，切割工艺比较简单，板材利用率较高。构造了生成该种排样方式的背包算法，并和线性规划算法相结合设计了基于FBUS排样方式的下料算法。算法时间复杂度较低，易于实现相应下料软件，能够有效地解决矩形件需求量较大的TCS问题。

[1] Wäscher G, Haußner H, Schumann H. An improved typology of cutting and packing problems [J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.

[2] 邓应波, 祝胜兰, 饶运清. 一种针对绝缘纸板排样的混合算法[J]. 机械设计与制造, 2013, (3): 23-25.

[3] Andrade R, Birgin E G, Morabito R. Two-stage two-dimensional guillotine cutting stock problems w ith usable leftover [J]. International Transactions in Operational Research, 2016, 23(1/2): 121-145.

[4] Hifi M, Negre S, Ouafi R, et al. A parallel algorithm for constrained two-staged two-dimensional cutting problems [J]. Computers & Industrial Engineering, 2012, 62(1): 177-189.

[5] Cui Y D, Huang B X. Heuristic for constrained T-shape cutting patterns of rectangular pieces [J]. Computers & Operations Research, 2012, 39(12): 3031-3039.

[6] Cui Y D. Heuristic for two-dimensional homogeneous two-segment cutting patterns [J]. Engineering Optim ization, 2013, 45(1): 89-105.

[7] Cui Y D. A new dynam ic programm ing procedure for three-staged cutting patterns [J]. Journal of Global Optim ization, 2013, 55(2): 349-357.

[8] 潘卫平, 陈秋莲, 崔耀东, 等. 基于匀质条带的矩形件最优三块布局算法[J]. 图学学报, 2015, 36(1): 7-11.

[9] 陈学松, 曹 炬, 方仍存. 遗传模拟退火算法在矩形优化排样系统中的应用[J]. 锻压技术, 2004, 29(1): 27-29.

[10] 崔耀东. 生成矩形毛坯最优T形排样方式的递归算法[J].计算机辅助设计与图形学学报, 2006, 18(1): 125-127.

[11] Cui Y D. Generating optimal T-shape cutting patterns for rectangular blanks [J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2004, 218(8): 857-866.

[12] Kellerer H, Pferschy U, Pisinger D. Knapsack problems [M]. Berlin: Springer Berlin Heidelberg, 2004: 211-234.

A Determ inistic Algorithm for Solving the Problem of Two-Dimensional Sheet Cutting Stock

Zeng Zhaom in1, Wang Jihong2, Guan Weili3

(1. Sichuan Institute of Information Technology, Guangyuan Sichuan 628017, China; 2. School of Electrical Engineering, Zhengzhou University of Science＆Technology, Zhengzhou Henan 450064, China; 3. Information Engineering College, Nanning University, Nanning Guangxi 530200, China)

This paper discusses the two dimensional sheet cutting stock problem, that is, use the least number of sheets to cut out a certain number of rectangular pieces. A determ inistic algorithm is proposed which based on the combination of knapsack algorithm and linear programm ing algorithm. First, a knapsack algorithm is constructed to generates the four blocks uniform strip pattern, then the linear programm ing algorithm is used to generate the cutting plans which iteratively calls the above knapsack algorithm to improve the objective function based on the principle of m inimum production cost and changes the current value of punched items to generate a new pattern according to the current value. Lastly, a set of optimal cutting patterns is selected to form the cutting scheme. The algorithm was compared w ith the famous T-shape algorithm using some benchmark problem tests. The results show that the algorithm can save more sheets than the T-shape one, and the calculation time is reasonable in practical application.

two-dimensional cutting; rectangle cutting stock; knapsack algorithm; linear programm ing algorithm

TP 399

10.11996/JG.j.2095-302X.2016040471

A

2095-302X(2016)04-0471-05

2015-12-19；定稿日期：2016-02-03

四川省教育厅科研项目(GZY1 5C4 5)；广西科学研究与技术开发计划项目(1 2 1 1 8 0 1 7-1 0A)

曾兆敏(1974−)，女，四川西昌人，本科，副教授。主要研究方向为并行计算、计算机硬件。E-mail：zengzmsc@163.com

管卫利(1977−)，男，广西桂林人，硕士，副教授。主要研究方向为优化算法、人工智能。E-mail：1430571958@qq.com