卵圆方程研究
2016-12-01李湘江
李湘江
(长沙理工大学计算机与通信工程学院,湖南 长沙 410114)
卵圆方程研究
李湘江
(长沙理工大学计算机与通信工程学院,湖南 长沙 410114)
卵圆是生活中非常常见的图形,但数学和工程学中对卵圆没有明确的定义。对于卵圆的研究仍然停留在圆和椭圆的阶段。根据卵圆的描述性定义,给出了卵圆的卵心、卵圆的长半径、卵圆的短半径和卵圆的对称半径等概念,经过严格的数学分析和推导首次提出了一种三次卵圆方程及标准卵圆方程。给出某些三次方程是否为卵圆方程的判别方法,以及卵圆长、短半径和卵圆对称半径的求法。在一定程度上解决了卵圆无单一数学表达的问题。通过对真实鸡蛋照片的图像分析,取得照片中鸡蛋的长、短半径和对称半径的实际参数值,代入卵圆方程,运用计算机程序绘制卵圆方程图形,与真实鸡蛋照片进行比照,能达到高度吻合的效果。
卵圆;卵圆方程;卵心;长半径;短半径;对称半径
自然界是如此的美妙和神奇,为科学与工程学提供了各种各样的素材和灵感。人们从抛体运动获得了抛物线及其方程,从天体运动获得了椭圆及其方程,而常见的各种鸟类、禽类和爬行动物的卵的纵截面形状,被人们习惯地称之为卵圆或卵形线。尽管人们对卵圆的直观认识由来已久,但至今未能对卵圆有一个明确的定义,仍然停留在圆[1]和椭圆[2]阶段,更未能给出卵圆的曲线方程;卵圆曲线大都是通过圆和椭圆的拼凑或组合形式即分段函数的形式给出[3]。本文通过分析,获得了三次曲线中的一种卵圆方程及标准卵圆方程。
1 卵圆及其相关概念
众所周知,卵圆类似于椭圆,但是一头大,一头小,且有一条对称轴。这可视为卵圆的一种描述性定义。若取这条对称轴为x轴,小头方向为x轴的正向,把通过卵圆上、下的两个顶点S、T的直线设为y轴,并设卵圆与x轴的两个交点即卵圆左、右两个顶点为Q、P。并将线段ST与PQ的交点即坐标系的原点O(0,0)称为卵圆的卵心,线段OP称为卵圆的长半径,其长度记为a;线段OQ称为卵圆的短半径,其长度记为b;线段OS(或OT)称为卵圆的对称半径,其长度记为c。线段PQ称为卵圆的直径,其长度记为d,显然d = a + b,线段ST称为卵圆的对称直径,显然ST = 2c。并将卵圆的长、短、对称半径a、b、c称为卵圆的3个特征参数。卵圆及其在直角坐标系的示意图如图1所示。

图1 卵圆及其在直角坐标系示意图
2 卵圆方程推导
下面来探求以正数a、b、c (a>b)为卵圆的长、短、对称半径,以原点O(0,0)为卵心的卵圆的方程。
一般的二次方程表达式为

上式所表示的曲线不外乎为椭圆(圆是椭圆的特例)、抛物线、双曲线,或脱化成两条直线或一点,或者为空集[4]。故卵圆方程不可能在二次方程中找到。
因此转而考虑如下的三次方程

因为卵圆是关于x轴对称的,故其方程中,关于y的一次项不能出现,而关于y的平方项一定出现;又卵圆不经过原点,故式(1)中的常数项不能为零。因此式(1)中只有当第二、五、七项不出现时,才有可能成为卵圆方程,于是卵圆方程可在如下的三次方程中来寻找
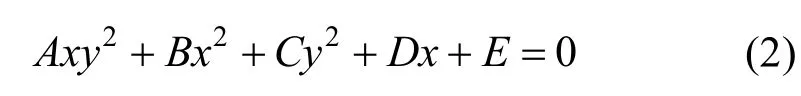
其中,系数A、B、C、D、E均不为零。
下面进一步探求式(2)中的系数要满足何种条件方能成为卵圆方程呢?为此,用 A(A≠0)去除式(2)的两边,令首项(三次项)的系数为1,得到
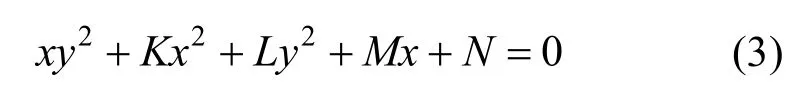
(4)
当已知卵圆的长、短和对称半径分别为a、b、 c (a>b)时,可确定卵圆方程式(3)中的系数K、L、M、N。为此,先将式(3)变成显函数形式

并求出导数,得到化简式
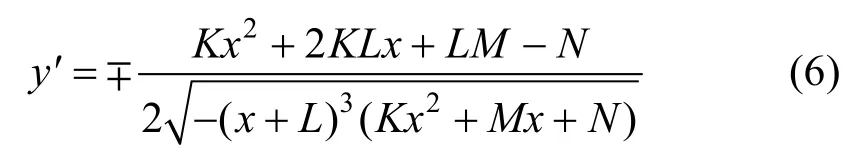
因为顶点P(a,0)、Q(-b,0)、S(0,c)均在卵圆上,故这3点的坐标应满足式(3),从而得到
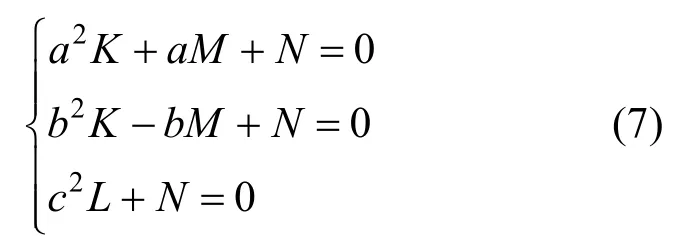
又顶点S(0,c)应是卵圆曲线的极值点,故在x=0处的导数等于零,从而由式(6)得到

联立式(7)、(8)即可解得

将式(9)代入式(3),即得

或

或

式(10)~(13)就是已知卵圆的长、短、对称半径a、b、c的3个特征参数,以原点O(0,0)为卵心的卵圆方程。其中式(12)称为卵圆的标准方程。
由式(9)可知:K>0、L>0、M<0且N=LM,故卵圆方程又可表示为

其中,K>0、L>0、M<0。且由式(9)的前3个等式反解之,可得卵圆的长、短、对称半径

又比较式(2)与式(11)可得

故知,当A>0、B>0、C>0时
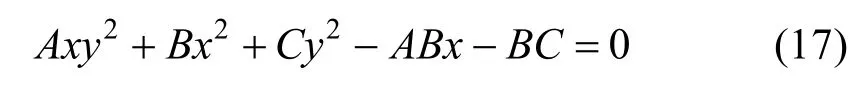
式(17)为卵圆方程,且由式(16)的前3个等式反解可得卵圆的长、短、对称半径

在式(12)及式(13)中,令

则知,当α>0、β>0、γ>0时
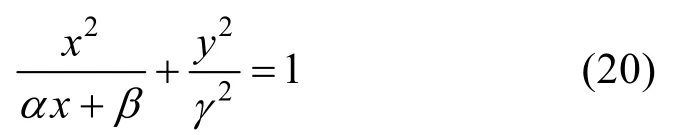
均亦为卵圆方程,且由式(19)反解可得卵圆的长、短、对称半径

当b=a时,即卵圆的短半径与长半径相等时,由式(12)可得

式(23)即为椭圆方程。故卵圆是椭圆的扩充或推广,而椭圆是卵圆的特款。
3 实例与仿真验证
3.1 实例
下面给出一个具体的三次卵圆方程,取a=6、b=4、c=3,则由式(10)或式(11)、式(12)、式(13)即得其卵圆方程

方程式(24)在区间[-4,6]上,用计算机绘制的图形如图2所示。
或
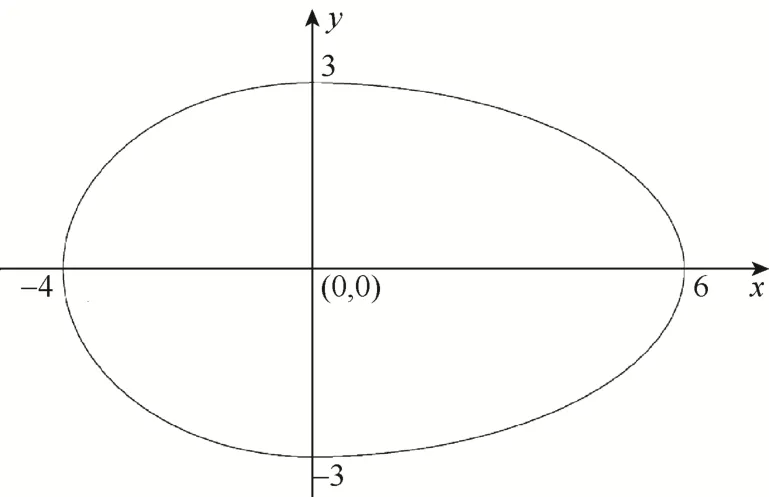
图2 方程式(24)的图形
3.2 仿真验证
图 2的图形看上去像一个卵圆,直观上符合卵圆的描述性定义。但到目前为止,数学和工程学对卵圆还没有明确定义。为了验证本文所建卵圆方程图形效果,在网上下载了一张鸡蛋的照片,
如图3所示。
图 3是未做任何修改的原照片,只将图片进行旋转并剪裁成合适大小,用 VB6.0编写了一个绘图程序。程序界面上的绘图区将鸡蛋照片作为绘图背景。通过像素分析和计算,获得图片中鸡蛋图像横向最大像素为386,纵向最大像素为294,在鸡蛋图像横向和纵向最大像素处画两条直线作为x、y轴,x轴与y轴的交点即为鸡蛋的卵心,并将卵心位置设定为绘图区的原点。程序界面如图4所示。

图3 鸡蛋照片

图4 绘图程序界面
按卵圆方程的需求量取鸡蛋以像素为单位的长、短、对称半径3个参数值,得出a=206、b=180、c=147。则由式(13)即得其卵圆方程

绘图程序使用方程式(25)在区间[-180,206]中进行计算并通过描点法绘制图形。程序界面右侧文本框中显示方程取点的计算值。程序运行结果如图5所示。
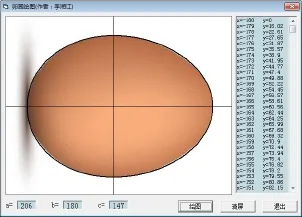
图5 绘图程序运行结果
图 5中鸡蛋外轮廓的黑色图线是绘图程序根据卵圆方程式(25)绘制的卵圆图形,与图片中鸡蛋外轮廓高度重合。这充分说明本文所得卵圆方程的图形确实是卵圆。
4 结 论
在工程中,绘制卵圆及卵形曲线通常是用多段圆弧来近似连接而成,或由经过若干个点的自由曲线构成,或以椭圆为初始曲线利用几何变换生成[5],或利用多焦点圆及椭圆生成[3]等方法,在高等级公路工程设计与计算中卵形曲线就是难度较大的一种曲线[6]。上面从卵圆的描述性定义出发,在三次方程中得到了一种卵圆方程,解决了卵圆无单一数学表达式的问题。有了卵圆方程就可以通过计算机绘制精确的卵圆曲线,比其他辅助方法绘制的卵圆曲线更快捷、优美,实现了计算机绘制卵圆图形最快速、最直接的方法。可以预见,由于有了这种卵圆的三次方程,将会给卵圆及其应用研究带来极大方便。
[1] 刘绍学. 数学必修 2[M]. 北京: 人民教育出版社, 2007: 118-122.
[2] 刘绍学. 数学选修 2-1[M]. 北京: 人民教育出版社, 2007: 38-40.
[3] 管贤根, 管 杰. 多焦点圆及其椭圆和卵圆[J]. 图学学报, 2013, 34(2): 52-64.
[4] 吴光磊, 丁石孙, 姜伯驹, 等. 解析几何[M]. 北京:人民教育出版社, 1979: 128-129.
[5] 宋业存, 祝燕琴. 一种生成卵形曲线的方法[J]. 工程图学学报, 2006, 27(1): 160-163.
[6] 张家平, 陈化新, 于文勇. 运用切基线法测算卵形曲线要点解析[J]. 测绘工程, 2010, 19(1): 17-20.
The Study on the Oval Equation
Li Xiangjiang
(School of Computer and Communication Engineering, Changsha University of Science & Technology, Changsha Hunan 410114, China)
Oval is a very common graphics in life, however it is not clearly defined in mathematics and engineering. It is still in the stage of circle and ellipse for studying the oval. In this paper, according to the descriptive definition of oval, a kind of cubic and standard equation is firstly given by mathematical analysis and derivation. A determ ining method is proposed whether a cubic equation is an oval equation or not, and the approach is given about how to calculate long, short and symmetry radius. To some extension, the proposed method can solve the problem about the oval w ithout a mathematical expression. By analyzing the real images of an egg, the real parameter values of long, short and symmetry radius are obtained. These values are input to the oval equation, the graphics is drawn using computer program. Compared w ith the real images of eggs, the highly consistent results can be achieved.
oval; oval equation; oval center; long radius; short radius; symmetric radius
O 182.1
10.11996/JG.j.2095-302X.2016040467
A
2095-302X(2016)04-0467-04
2015-12-15;定稿日期:2016-01-05
李湘江(1972−),男,湖南湘阴人,高级实验师,高级程序员,硕士。主要研究方向为图形图像、软件工程及计算机测控。E-mail:cslixj@163.com
