五年级学生计算错误的思考与实践

杨淑君

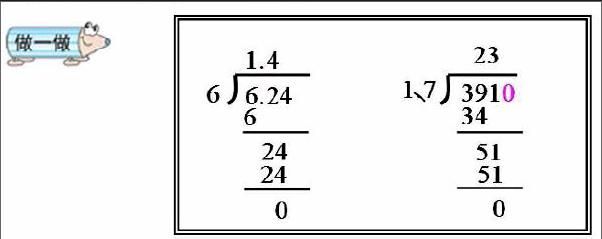
【摘 要】计算教学一直有相当重要的地位。很多教师在批改作业时都会发现，有很多学生并不是不会做计算题，而是会做而做不对。作为教师必须认真分析错误原因，讲清算理和法则，运用迁移，加强方法的指导，并培养学生的计算习惯和兴趣，减少错误率。

【关键词】计算错误；归因；策略

时常听到这样的议论，某某学生真粗心，这不，这道题又做错了。而学生面对自己的错误，也是怪自己太粗心了。一旦把原因归结为粗心之后，学生就不再重视自己的错题，把它扔在一边。怎样让学生正确的看待自己的错题，养成科学的“订正习惯”，进而发展正确的错误观。

一、“乱花渐欲迷吾眼”——真是太粗心了吗？怎么会又错？

现象描述：我把题目抄错了。

某天上完一个数除以整数，我给学生留了几道练习题，其中有一题是35÷14，居然有4个学生做上来是53÷14，还有一个学生跑到办公室来问我说：“老师这道题目你出错了，除不尽的。”这些学生订正以后，都觉得是自己太粗心，把题目抄错了。几天后进行单元测试，3.484÷5.2，也有4个学生做成3.484÷2.5，其中两个是前面提到的学生。学生把题目抄错，真的是太粗心吗？

现象描述：我“0”、“.”忘记写了。

学完小数除法，我们的学生总是“忘记”这，“忘记”那。328÷16=2.5（正确答案328÷16=20.5），学生说我中间忘记商“0”了；108÷24=45（正确答案108÷24=4.5），学生说我忘点小数点了。而同样的错误他们照犯不误。“0”、“.”真的是忘记写了吗？

如何少发生计算错误，提高计算的正确率，多数教师和学生对这一问题的解释通常是“太粗心，仔细点”，这种解释过于笼统，致使学生不知道到底该如何去掉粗心，有时候却越仔细，越容易出错。久而久之，学生对错题在无可奈何之下便靠所谓的“运气”了，连他自己也不知道自己到底做对没有。

事实上，这种困惑几乎是伴随着大多数学生的学业成长，也伴随着教师教学生涯的始终：学生明明会做，却要做错？

二、“众里寻她千百度”——怎能一个“粗心”了得！其实是这样的……

粗心不是错误的原因，致使学生做错题目的很可能是概念、法则理解不清；计算技能缺陷、受思维负迁移的影响等有形的可表述可针对的原因，因此，错误的改正必须是有针对的，而不是笼统的“仔细”。

（一）概念、法则理解不清

概念和法则是学生进行数学计算的重要依据。小数乘除法的计算方法是建立在整数计算的基础上的，是由“数位”、“个位”、“相加”、“满十”、“前一位”、“进一”等一系列数学概念组成的。如果概念不清，就无法依照法则、定律、性质、公式等数学知识正确计算。案例1：

像上面，6.24÷6=1.4，391÷1.7=23。错误的原因是学生对以下概念不够清晰：除到被除数的哪一位不够商1，就在那一位上面商0，这里学生对0的占位作用认识不够以及在什么情况下应该用0占位这一知识点没有掌握好。

（二）受思维负迁移的影响

迁移是一种学习对另一种学习的影响，有积极的作用，也有消极的作用。思维的负迁移就对数学计算有消极的影响。

案例2：一位教师在教学完小数除以整数后，向学生出示了这样一道改错题：“小明和大家一样，也学习了小数除以整数的笔算，你来当小老师检查一下，他做得对吗？”

当天的课堂作业中竟然有5位学生按错题的方法进行笔算。这样的改错题不仅对促进学生的发展没有好处，而且还会产生一定的误导和负迁移

再例如：计算7.75+1.25×3.4=9×3.4=30.6。错误的原因是学生受到容易计算部分、能简便计算、比较熟悉部分等强烈刺激的作用而造成思维负迁移。

（三）计算技能缺陷

一些同学计算错误很多，有可能是计算能力不足引起的。比如：乘法口诀不熟、进位加法不熟、试商能力不足等；可能缺少一种良好的计算习惯或书写习惯，如验算的习惯等；许多学生在计算时，忽视了“估算”的作用。这一点可能是我们平时教多练少的关系。

三、“柳暗花明又一村”——不都是粗心惹的，原来如此！

（一）讲清算理和法则

正确的运算必须建筑在透彻地理解算理的基础上，学生的头脑中算理清楚，法则记得牢固，做四则计算题时，就可以有条不紊地进行。

小学生遇到的算理如：10以内数的组成和分解，凑十法和破十法，相同数连加的概念，十进制计数法，有关数位的概念，小数的意义与性质，小数点位置的移动引起小数大小的变化，积、商的变化规律，分数的意义与性质，分数单位的概念，分数与除法的关系，约分与通分等概念。

以上这些基础知识，都应讲解得很清楚，使学生留下深刻的印象，以便在学习新知识时，能发挥知识的正迁移作用。

（二）注意运用法则之间的正负迁移

要充分发挥正迁移作用，防止负迁移的消极影响。在学习新的计算法则时，引导学生比较新旧知识点的异同点，使学生在比较中，能够明确新旧知识之间的多角度、多侧面的联系，新知识才会在学生已有认知结构中“生根”，使原有知识结构得到发展。

案例3：

（1）引导学生观察：7.98÷4.2和我们以前学过的小数除法算式有什么不同？

（2）把“7.98元”和“4.2元”转化成用角（或分）作单位的数量，目的都是把4.2从小数转化为什么数？

这里的教学就是抓住了新旧知识的异同和“把除数是小数转化为整数而商不变”这个小数除法法则算理的关键。帮助学生在新旧知识之间“铺路”，使学生已有知识与新知识发生联系。

（三）对学生的计算技能适当地作指导

新课程的很多理念在教师们的心中扎下了根，但对于计算，虽然没有片面追求方法的多样化，但有些方法在学生的心中还有了一些影响，比如：课堂教学中不够重视学生的口算基本功的训练。老师一看是计算题，就完全推给学生，让学生在课下计算，学生的警惕性不高，老师重视的也不够。教师应改变教学观念，在教学在重视计算，对学生的计算技能适当的作一些指导。

四、结束语

了解学生计算能力现状，结合学生对计算的所需所想，知晓学生的思维过程、从实践与心理两方面分析影响学生计算错误的主要因素，掌握学生出错的基本题型，探索提高学生计算正确率的有效对策，及纠错所要注意的问题，探寻最佳纠错方案，实现计算教学理想化。

参考文献：

[1]刘克寿，刘霞，张京玉.浅谈小学生计算错误产生的原因[J].

[2]杨庆余.儿童计算中“粗心”错误的心理成因探析[J].数学教育，（标明年份）（7）.

[3]张洪霞.小学数学计算教学策略研究[D].东北师范大学，2012

[4]吴芳.小学生分数概念体系掌握情况的调查及对策研究[D].南京师范大学，2011

[5]王江.六年级学生分数计算能力的培养及其对分数应用能力的影响[D].华东师范大学，2011

[6]范晓琳.采用多元表征教学策略对小学五年级学生进行分数概念转变的干预研究[D]. 内蒙古师范大学，2009