G550高强冷弯薄壁槽钢受弯构件力学性能与设计方法

赵金友 王钧 董俊巧

摘 要：为了研究高强冷弯薄壁槽钢受弯构件的力学性能和设计方法，对3种板件加劲形式的G550高强冷弯薄壁型钢槽形截面受弯构件进行了试验研究和有限元参数分析。结果表明，板件加劲形式对高强冷弯薄壁槽钢受弯构件屈曲模式和受弯承载力有显著影响，翼缘V形加劲比腹板V形加劲能够更有效地提高构件抗弯承载力，构件抗弯承载力的变化规律与屈曲模式有关。根据有限元参数分析结果，在已有直接强度法基础上回归出适用于高强冷弯薄壁槽钢受弯构件的直接强度法修正公式。

关键词：高强冷弯薄壁槽钢；受弯构件；力学性能；直接强度法；抗弯承载力

中图分类号：TU392.1

文献标志码：A文章编号：1674-4764（2016）05-0099-09

Abstract：Static test and finite element analysis of high strength cold-formed thin-walled channel flexural members with three types of stiffeners in the flanges and the web were conducted respectively to investigate the mechanical properties and design method of G550 high strength cold-formed thin-walled channel flexural members. The results showed that stiffener type had a significant effect on the members bending strength and buckling modes. V type stiffeners in the flanges could increase the bending strength more significantly than V type stiffeners in the web. The change law of the bending strength was related to the buckling mode. Based on the existing direct strength method （DSM） formulas as standard， the revised DSM formulas of high strength cold-formed thin-walled channel flexural members were established according to finite element analysis results.

Keywords：high-strength cold-formed thin-walled channel steel； flexural members； mechanical properties； direct strength method； bending strength

G550高强钢材的力学性能与传统的Q235和Q345钢材有较大区别。中国《冷弯薄壁型钢结构技术规范》（GB50018—2003）对屈服强度高于Q345、板厚小于2 mm的构件尚无明确的设计条款。Yang等[1]、Young[2]、周天华等[3]和李元齐等[4]学者相继开展了G550高强冷弯薄壁型钢受压构件稳定性能与设计方法的试验与理论研究。目前，对G550高强冷弯薄壁型钢受弯构件的研究报道尚不多见[5-6]。

直接强度法（Direct Strength Method，简称DSM）是Schafer和Pekz提出的新的冷弯薄壁型钢构件设计方法[7-8]，它摒弃了传统有效截面法的计算方法，把整个截面作为一个对象来考虑，大大简化了计算过程，并且将畸变屈曲进行了单独计算[9-10]。但是直接强度法关于受弯构件设计公式的试验数据仅来自屈服强度较低的冷弯薄壁型钢C形和Z形截面[11]，对于屈服强度较高的冷弯薄壁型钢受弯构件承载力计算的直接强度法尚需进一步开展试验研究与理论分析[12]。

本文在对无加劲、翼缘V形加劲以及翼缘和腹板V形加劲的G550高强冷弯薄壁槽钢受弯构件试验研究和有限元参数分析的基础上，研究高强冷弯薄壁槽钢受弯构件的力学性能，并根据经试验验证的有限元参数分析结果回归出G550高强冷弯薄壁槽钢受弯构件承载力计算的直接强度法公式，为修订相应规范和推广G550高强钢材应用提供参考。

1 试验研究

1.1 试件设计及编号

试件截面形式如图1所示，选取了3种板件加劲形式，分别为无V形加劲、翼缘V形加劲以及翼缘和腹板V形加劲。每种板件加劲形式根据卷边宽度分别为短卷边和长卷边2组试验，共计6组试验。每组试验有截面相同的2个试件。

试件采用镀铝锌钢板加工制作而成，钢板名义厚度t=1.2 mm。试件的腹板高H=160 mm，翼缘宽B=80 mm。每种截面形式的短卷边和长卷边分别为10、30 mm。V形加劲肋两板件间夹角为直角，加劲肋高度Sf1=Sw1=10 mm，宽度Sf=Sw=20 mm。

试件的编号规则如图2所示。试验前采用游标卡尺测量了试件的实际几何尺寸，表1列出了各试件的实测几何尺寸。钢板厚度实测值为1.24 mm。

1.2 材料属性及试件初始缺陷

试件采用G550冷轧镀铝锌钢板冷弯而成，通过标准试件拉伸试验确定试件材料属性。材性试验结果为：名义屈服强度f0.2=628 MPa，抗拉强度fu=683 MPa，弹性模量E=1.98×105 MPa，伸长率δ=10.5%。

已有研究表明，薄壁构件的承载力受初始几何缺陷的影响较大[13]。因而采用文献[11]的方法测量了试件研究区段受压翼缘的局部初始几何缺陷Δl和畸变初始几何缺陷Δd。

无V形加劲试件、翼缘V形加劲试件以及翼缘和腹板V形加劲试件Δmaxd/t的平均值分别为0.11、1.16和0.99，Δmaxl/t的平均值分别为2.10、2.11和1.99。

1.3 加载装置

试验时，2个截面形式完全相同试件的腹板在支座处和加载处通过高强螺栓分别与支座连接件和加载连接件连接在一起，即2个截面相同试件采用背靠背方式连接。荷载通过加载处试件腹板与高强螺栓间的摩擦力均匀传到2个试件上。

试验采用三分点加载。试件长2 820 mm，中间900 mm的纯弯区段为试验的研究区段，为了防止两侧非纯弯区段的影响，在非纯弯段受压翼缘加设厚为6 mm的盖板，盖板与试件受压翼缘通过高强螺栓相连。图3所示为试验加载装置，利用螺旋千斤顶手动加载，每级加载量及试件极限承载力可通过传感器的读数获得。

1.4 试验结果

1.4.1 屈曲模式 由于短卷边对翼缘发生畸变屈曲的约束作用较弱，所有短卷边试件均发生了畸变屈曲，如图4（a）所示；由于长卷边对翼缘的约束作用较强，无加劲长卷边试件发生了局部屈曲，如图5（a）所示；对翼缘V形加劲以及翼缘和腹板V形加劲长卷边试件来说，由于翼缘加劲提高了板件的局部屈曲临界应力，试件发生了局部与畸变的相关屈曲，荷载作用点附近的受压卷边发生了局部屈曲，同时，试件受压翼缘与卷边的交线不再保持原有的直线状态，即试件有畸变屈曲出现，如图6（a）所示。

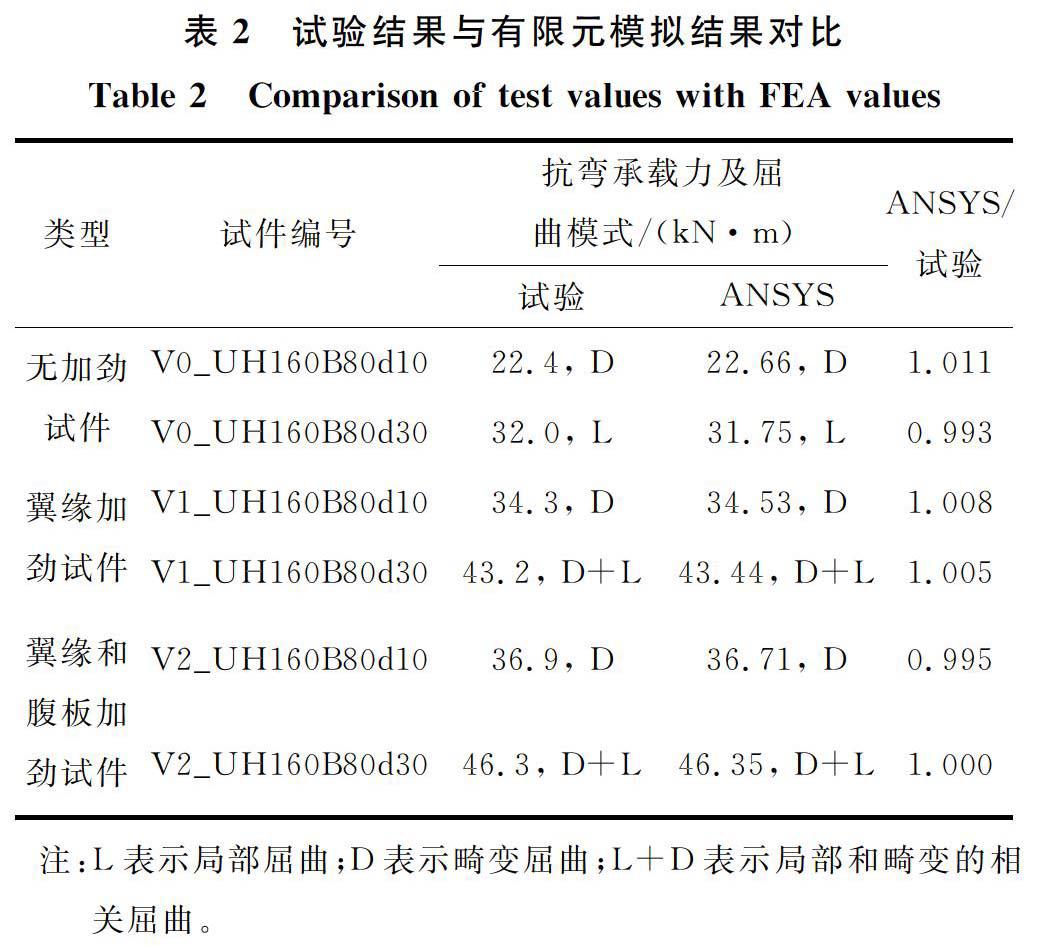
1.4.2 抗弯承载力 表2为试件抗弯承载力对比表，从表2可以看出，同种截面情况下，长卷边试件的抗弯承载力均高于短卷边试件；同种卷边宽度情况下，无V形加劲试件最低，翼缘V形加劲试件次之，翼缘和腹板V形加劲试件抗弯承载力最大。翼缘V形加劲试件以及翼缘和腹板V形加劲试件的抗弯承载力比无加劲试件的抗弯承载力高35%～65%，而翼缘V形加劲试件仅比翼缘和腹板V形加劲试件的抗弯承载力低8%以内。分析认为，受弯构件腹板上的应力呈梯度分布，而受压翼缘由于承受均布压应力可能先发生屈曲，所以受弯构件采用翼缘V形加劲比腹板V形加劲能够更有效地提高其抗弯承载力。

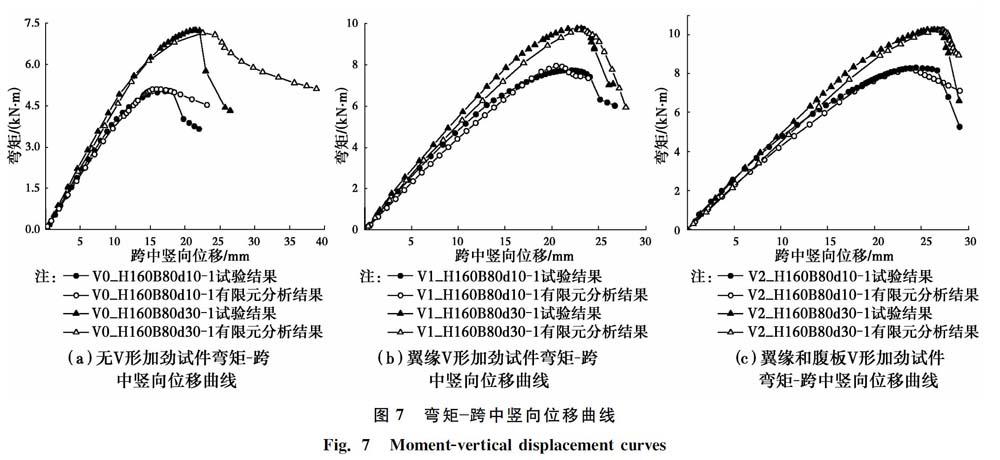
1.4.3 弯矩跨中竖向位移曲线 图7（a）、（b）和（c）所示分别为无V形加劲试件、翼缘V形加劲试件以及翼缘和腹板V形加劲试件的弯矩跨中竖向位移曲线。从图7可见，长卷边试件的承载力远大于短卷边试件，而且所有试件弯矩跨中竖向位移曲线的下降段较陡，这是由于试验所选名义屈服强度为550 MPa的钢材具有强度高、延性差的特点。

1.5 有限元模拟结果与试验结果对比

采用有限元软件ANSYS12.0中的SHELL181壳单元对所有试件进行了模拟[13] 。文献[14]的研究表明，残余应力和冷弯加工引起的构件弯角处钢材屈服强度提高对构件承载力有着相反作用的影响，即二者的作用可认为能够相互抵消，因此笔者在进行非线性分析时没有考虑残余应力和冷加工的影响。有限元模拟求解过程分为两个阶段：第1阶段进行弹性特征值屈曲分析，确定无初始几何缺陷受弯构件可能出现的第1屈曲模态，将此第1屈曲模态作为非线性分析时的屈曲模态；第2阶段进行考虑几何和材料的双重非线性分析，采用理想弹塑性双折线模型，强化段斜率取所测弹性模量E的2%，分析时按实测初始缺陷施加缺陷值，按材性试验测得数据输入材料属性[15]。有限元模拟的试件屈曲模式分别如图4（b）、5（b）和6（b）所示，有限元模拟所得抗弯承载力见表2，有限元模拟所得弯矩跨中竖向位移曲线见图7。结果表明：有限元模拟屈曲模态和试验屈曲模态基本一致；有限元模拟抗弯承载力与试验结果基本一致，误差在2%以内；有限元模拟弯矩跨中竖向位移曲线与试验曲线在荷载上升段的吻合较好，且二者极值点几乎一致，而在荷载下降段，有限元曲线和试验曲线出现偏离，试验曲线出现突然下降的趋势，而有限元曲线偏于理想化，总体来看，有限元与试验的曲线变化趋势吻合良好。由此可见，本文有限元模型分析具有较高的精度，有限元模拟结果能够正确反映试验，在此基础上可开展大量的有限元参数分析研究。

2 有限元参数分析

2.1 参数选取

构件截面几何参数的定义与试验时相同。根据以往研究表明，中国冷弯薄壁型钢槽形截面的高宽比多在2～2.93，作为受弯构件，应该尽量增大其截面绕中和轴的惯性矩，以增大其抗弯承载力，为了对比不同高宽比构件的抗弯承载力，参数分析时选取了高宽比在2～3的不同截面。选取3种腹板高度分别为160、180和200 mm，腹板高度为160 mm时对应翼缘宽度分别为70和80 mm，腹板高度为180和200 mm时分别对应翼缘宽度为70、80和90 mm。为了研究卷边对构件抗弯承载力的影响，每种翼缘宽度对应2种卷边宽度分别为10和30 mm，选取4种板件厚度分别为0.6、0.75、1.0 mm和1.2 mm。板件加劲形式为无V形加劲、翼缘V形加劲以及翼缘和腹板V形加劲3种。

有限元参数分析时采用了与模拟试验一致的模型。钢材屈服强度fy=550 MPa，弹性模量E=2.06×105 MPa，泊松比ν=0.3。参考试验实测初始缺陷值施加初始缺陷。

2.2 有限元参数分析结果

2.2.1 屈曲模式 有限元参数分析发现：短卷边构件在特征值屈曲分析中表现为畸变屈曲，在非线性分析中一般以畸变屈曲为主（见图8）；长卷边构件在特征值屈曲分析中表现为局部屈曲，在非线性分析中表现有所不同，其中：翼缘V形加劲以及翼缘和腹板V形加劲构件表现为局部和畸变的相关屈曲（见图9），无V形加劲构件表现为局部屈曲（见图10）。

2.2.2 抗弯承载力 有限元参数分析抗弯承载力结果列于表3中。从表3结果可以看出与试验结果相同的规律，同种卷边宽度情况下，无V形加劲构件最低，翼缘V形加劲构件次之，翼缘和腹板V形加劲构件抗弯承载力最大。构件抗弯承载力的变化规律与屈曲模式有关，当发生畸变屈曲或局部和畸变的相关屈曲时，多数构件抗弯承载力随着翼缘宽度增加而增加（见图11 （a））；当发生局部屈曲时，构件抗弯承载力随着翼缘宽度增加而减小，如无加劲长卷边试件（见图11 （b）），这是由于无加劲长卷边构件受压翼缘发生了局部屈曲，板厚相同时构件随着翼缘宽度的增大容易出现局部屈曲。

3 直接强度法（DSM）修正公式的建立

3.1 DSM公式简介

Schafer等[16]提出了考虑局部和整体的相关屈曲以及畸变屈曲的直接强度法公式。

局部和整体的相关屈曲设计公式为

上述直接强度法受弯构件设计公式是利用屈服强度较低的受弯试件试验数据回归得来的。随着高强超薄钢材的出现，DSM的适用性和有效性需要进一步验证[19]。

3.2 DSM公式修正

原始的DSM公式把局部屈曲和畸变屈曲用不同的计算公式考虑，没有单独考虑局部和畸变的相关屈曲。本文研究发现，当构件的特征值屈曲分析表现为畸变屈曲时，其非线性分析通常表现为畸变屈曲；而当构件的特征值屈曲分析表现为局部屈曲时，其非线性分析通常表现为局部屈曲或局部和畸变的相关屈曲。因而建立DSM计算公式时将构件分为两类：一类考虑畸变屈曲，一类考虑局部屈曲以及局部和畸变的相关屈曲。为了使回归公式更具有普遍性，不区分加劲形式，将所研究的3种加劲形式构件综合考虑。

本文以192个有限元分析算例为依据，建立G550高强冷弯薄壁槽钢受弯构件承载力的DSM公式。由于本文分析的所有构件均限制其发生整体屈曲，所以建立的DSM 曲线不包括整体屈曲的内容，用截面边缘屈服弯矩My代替原始DSM计算公式中的Mne。取有限元分析所得构件抗弯承载力与My的比值Mu/My作为纵轴，λl=（My/Mcrl）0.5或λd=（My/Mcrd）0.5作为横轴（Mcrl和Mcrd可通过有限条程序CUFSM[20-21]求得），绘制二者之间的散点图，最终拟合得到修正后的DSM曲线，如图11所示。

图12（a）所示为发生局部屈曲以及局部和畸变相关屈曲的散点分布情况，可以看出3种加劲形式构件的散点分布大多数位于原始DSM曲线的下方，说明原始曲线偏于不安全，需对其进行修正。分析认为，相对于普通冷弯薄壁型钢而言，高强冷弯薄壁型钢厚度更薄，板件宽厚比更大，构件更易于发生局部屈曲失稳破坏，这使得发生局部屈曲以及局部和畸变相关屈曲的构件抗弯承载力Mu相对较小，在截面边缘屈服弯矩My一定的情况下，图12（a）中纵轴值也即Mu与My的比值Mu/My相对较小，最终导致构件的散点分布大多数位于原始DSM曲线的下方。

图12（b） 为发生畸变屈曲的散点分布情况，可以看出，无加劲构件的散点位于原始DSM曲线的下方且显著低于原始DSM曲线，有加劲构件散点大多数位于原始DSM曲线的上方且聚集在原始DSM曲线附近。对无加劲构件来说，原始DSM曲线偏于不安全，这是由于发生畸变屈曲的无加劲构件均为卷边宽d=10 mm的短卷边构件，短卷边对构件翼缘的约束较弱，使得更易于发生局部屈曲的无加劲构件首先发生了畸变屈曲，导致构件抗弯承载力Mu相对较小，在截面边缘屈服弯矩My变化不大的情况下，图12（b）中纵轴值也即Mu与My的比值Mu/My相对较小。因此，对于发生畸变屈曲的情况，仅需对无加劲构件进行适当修正。

修正后的局部和整体的相关屈曲设计公式为

有加劲构件的畸变屈曲设计公式无需修正，采用式（2）计算即可。

4 结 论

1）试验研究结果表明，板件加劲形式是影响受弯试件屈曲模式和承载力的重要因素。与无加劲形式相比，板件V形加劲有效减小了板件的宽厚比，提高了35%～65%的抗弯承载力，且翼缘V形加劲比腹板V形加劲能够更有效地提高试件抗弯承载力，有限元结果与试验结果吻合良好。

2）有限元参数分析结果表明，当构件的特征值屈曲分析表现为畸变屈曲时，其非线性分析通常表现为畸变屈曲；当构件的特征值屈曲分析表现为局部屈曲时，其非线性分析通常表现为局部屈曲或局部和畸变的相关屈曲。

3）高强冷弯薄壁槽钢受弯构件发生局部屈曲时，构件抗弯承载力随着翼缘宽度增加而减小；当发生畸变屈曲或局部和畸变的相关屈曲时，多数构件抗弯承载力随着翼缘宽度增加而增加。

4）以有限元参数分析为基础，建立了高强冷弯薄壁槽钢受弯构件的DSM修正公式，与DSM原始公式对比表明，本文提出的DSM修正公式对构件承载力的计算更为安全可靠，可为此类构件的实际工程应用和相应规范的进一步修订提供参考。

参考文献：

[1] YANG D，HANCOCK G J.Compression tests of high strength steel channel columns with interaction between local and distortional buckling [J].Journal of Structural Engineering，2004，130（2）：1954-1963.

[2] YOUNG B.Design of channel columns with inclined edge stiffeners [J].Journal of Construction Steel Research，2004，60（2）：183-197.

[3] 周天华，何保康，周绪红，等.高强冷弯薄壁型钢轴压短柱受力性能试验研究[J].建筑科学与工程学报，2005，22（3）：36-44.

ZHOU T H，HE B K，ZHOU X H，et al.Experimental research on bearing capacity of high-strength cold-formed steel stub columns [J].Journal of Architecture and Civil Engineering，2005，22（3）：36-44. （in Chinese）

[4] 李元齐，王树坤，沈祖炎，等.高强冷弯薄壁型钢卷边槽形截面轴压构件试验研究及承载力分析[J].建筑结构学报，2010，31（11）：17-25.

LI Y Q，WANG S K，SHEN Z Y，et al.Experimental study and load-carrying capacity analysis of high-strength cold-formed thin-walled steel channel column under axial compression [J].Journal of Building Structures，2010，31（11）：17-25. （in Chinese）

[5] 赵金友，董俊巧，王钧，等.不同截面形式高强冷弯薄壁槽钢构件受弯承载力试验研究[J].建筑结构学报，2015，36（5）：18-26

ZHAO J Y，DONG J Q，WANG J，et al.Experimental study on bending strength of high-strength cold-formed thin-walled steel channel section members [J].Journal of Building Structures，2015，36（5）：18-26. （in Chinese）

[6] 赵金友，王钧，冯巍.550 MPa高强冷弯薄壁卷边槽钢受弯构件畸变屈曲试验研究[J].土木工程学报，2016，49（1）：53-61.

ZHAO J Y，WANG J，FENG W.Experimental study on distortional buckling of 550 MPa high strength cold-formed thin-walled channel flexural members [J].China Civil Engineering Journal，2016，49（1）：53-61. （in Chinese）

[7] 王春刚，张壮南，张耀春.冷弯薄壁斜卷边槽钢轴压构件承载力计算的直接强度法研究[J].工程力学，2012，29（3）：75-82.

WANG C G，ZHANG Z N，ZHANG Y C.Direct strength method study on bearing capacity calculation of channel columns with inclined simple edge stiffeners under axial compression [J].Engineering Mechanics，2012，29（3）：75-82. （ in Chinese）

[8] DENIZ A，SCHAFER B W.Cold-formed steel member bending stiffness prediction [J].Journal of Construction Steel Research，2015，115（12）：148-159.

[9] 王春刚，张乃文，马平.板件中间加劲的复杂卷边槽钢轴压构件弹性畸变屈曲应力的实用计算方法[J].工业建筑，2014，44（5）：116-121.

WANG C G，ZHANG N W，MA P.A Simplified method for calculating elastic distortional buckling stress of channels with complex edge stiffeners and intermediate stiffeners under axial compressive load [J].Industrial Construction，2014，44（5）：116-121. （in Chinese）

[10] 姚兴友，李元齐.冷弯薄壁型钢卷边槽形截面构件畸变屈曲承载力计算方法研究[J].工程力学，2014，31（9）：174-181.

YAO X Y，LI Y Q.Distortional buckling strength of cold-formed thin-walled steel members with lipped channel section [J].Engineering Mechanics，2014，31（9）：174-181. （in Chinese）

[11] 王海明.冷弯薄壁型钢受弯构件稳定性能研究[D].哈尔滨：哈尔滨工业大学，2009：20-46.

WANG H M.Study on the stability behavior of cold-formed steel flexural members [D].Harbin：Harbin Institute of Technology，2009：20-46.（in Chinese）

[12] WANG L P，YOUNG B.Design of cold-formed steel channels with stiffened webs subjected to bending [J].Thin-Walled Structures，2014，85（12）：81-92.

[13] 王春刚，梁润嘉，张壮南.腹板开孔复杂卷边冷弯薄壁槽钢受弯构件稳定性试验研究[J].建筑结构学报，2014，35（4）：125-134.

WANG C G，LIANG R J，ZHANG Z N.Experimental investigation on stability behavior of channel flexuralmembers with complex edge stiffeners and web holes [J].Journal of Building Structures，2014，35（4）：125-134. （ in Chinese）

[14] DUBINA D，UNGUREANY V.Effect of imperfections on numerical simulation of instability behaviour of cold-formed steel members [J].Thin-Walled Structures，2002，40（3）：239-262.

[15] 姚谏，程婕，卢哲刚.冷弯薄壁卷边Z形钢梁的弹性畸变屈曲荷载[J].工程力学，2013，30（1）：81-86.

YAO J，CHENG J，LU Z G.Distortional buckling loads of cold-formed lipped zed-beams [J].Engineering Mechanics，2013，30（1）：81-86. （in Chinese）

[16] SCHAFER B W，PEKZ T.Direct strength prediction of cold-formed steel members using numerical elastic buckling solution [C]//Second international conference on thin-walled structures： Thin-Walled Structures Research and Development， Singapore， Elsevier Science Ltd， 1998：137-144.

[17] NADERIAN H R，RONAGH H R.Buckling analysis of thin-walled cold-formed steel structural members using complex finite strip method [J].Thin-Walled Structures，2015，90（5）：74-83.

[18] SHAHBAZIAN A，WANG Y C.Direct Strength Method for calculating distortional buckling capacity of cold-formed thin-walled steel columns with uniform and non-uniform elevated temperatures [J].Thin-Walled Structures，2012，53（4）：188-199.

[19] 钟炜辉，孟宝，郝际平.冷弯薄壁构件腹板局部受压承载力分析及设计建议[J].建筑结构，2015，45（5）：86-90.

ZHONG W H，MENG B，HAO J P.Local bearing capacity analysis for the web of cold-formed thin-wall member and design recommendation [J].Building Structure，2015，45（5）：86-90. （in Chinese）

[20] DONG S E，LI H R，WEN Q P.Study on distortional buckling performance of cold-formed thin-walled steel flexural members with stiffeners in the flang [J].Thin-Walled Structures，2015，95（9）：161-169.

[21] 于欣永，王春刚，贾连光.翼缘加劲的冷弯薄壁型钢受弯构件弹性屈曲应力研究[J].工程力学，2013，30（A1）：68-71.

YU X Y，WANG C G，JIA L G.Study on the elastic buckling stress of cold-formed steel flexural members with stiffeners in the flange [J].Engineering Mechanics，2013，30（A1）：68-71. （in Chinese）

（编辑 王秀玲）