钢筋混凝土无腹筋细长梁剪切破坏机理模型研究综述

邓清 易伟建 李烨

摘 要：根据现有关于钢筋混凝土无腹筋细长梁剪切破坏机理问题的研究成果，介绍了基于修正压力场理论的抗剪模型、临界剪切裂缝理论、塑性理论、压力路径理论、劈裂破坏理论和基于截面应变分析的抗剪模型的基本假设、核心观点及受剪承载力计算方法，并给出总结、归纳及评析；另一方面，利用相关试验数据和ACI-DAfStb无腹筋细长梁剪切破坏数据库，分别对不同理论模型的受剪承载力计算公式进行了设计参数的影响评估和统计评估；并展望了无腹筋细长梁剪切破坏机理研究的发展方向。研究结果表明：不同理论模型的部分假设缺少直接的试验依据支持，梁腹混凝土的受拉（劈裂）或受剪（骨料咬合）以及受压区混凝土对抵抗剪力的贡献成为抗剪机制的主要分歧；不同受剪承载力计算公式对不同影响因素的考虑方式的合理性和计算结果的准确度均有待进一步提高。后续深入研究应综合考虑剪切破坏问题的随机性和物理属性，利用先进测试技术、应力演化分析方法，进一步揭示剪切破坏机理。

关键词：无腹筋细长梁；剪切破坏；机理模型；受剪承载力

中图分类号：TU375.1

文献标志码：A文章编号：1674-4764（2016）05-0001-11

Abstract：Based on the review of domestic and foreign researches on the shear failure mechanism of slender reinforced concrete beams without shear reinforcement， the basic assumptions， the key points and the calculation methods for shear strength of different models were introduced and commented， such as the modified compression field theory， the critical shear crack theory， the plasticity theory， the compressive force path theory， the splitting failure theory and the strain based shear strength model. Using the test data from the related experimental programs and the ACI-DAfStb shear database of slender beams， impact assessments of important design parameters and statistical evaluations were conducted on the calculation methods for shear strength of different models. Some points of view on expectation of shear failure were presented. The results showed that the absences of direct experimental proofs of some hypotheses were apparent and different opinions on the shear transfer contribution of diagonal tension （splitting）， shear （aggregate interlock） and the flexural compression zone were the main divergence of the shear transfer mechanism. Further improvements in the rationality of the considerations for different factors and the accuracy of the calculation methods for shear strength were essential. In subsequent research work， the random and physical characteristics of shear failure should be considered synthetically. Advanced testing technology and analysis of the evolution of the stress field can be utilized in revealing the mechanism of shear failure.

Keywords：slender beams without shear reinforcement；shear failure；mechanism model；shear capacity

围绕钢筋混凝土无腹筋梁剪切破坏问题的研究工作始于20世纪初期。1955年，美国Wilkins空军仓库的刚架横梁发生典型的剪切破坏[1]，事故引发了学术界、工程界对钢筋混凝土梁剪切破坏问题的关注。近年来，学者们通过试验研究、理论分析方法对无腹筋梁的剪切破坏机理、影响因素及受剪承载力计算方法开展了广泛、深入的研究工作，对剪切破坏的影响因素、破坏模式及失效机理等问题形成了较为系统的认知，相继提出区别于半理论半经验公式和统计回归公式的机理模型，如基于修正压力场理论的抗剪模型、临界剪切裂缝理论、塑性理论、压力路径理论、劈裂破坏理论和基于截面应变分析的抗剪模型。

层出不穷的理论模型表明各界学者对剪切破坏的影响因素、破坏机理的认识在不断加深。但是与钢筋混凝土梁正截面理论体系比较，上述颇具代表性的理论模型之间主要存在如下差异：对ACI-ASCE 445抗剪研究报告[2]中确定的5种抗剪机制在不同受力阶段的贡献程度、失效机理存在不同认识；不同受剪承载力计算公式对混凝土强度、剪跨比、纵向配筋率和最大骨料粒径等影响因素的考虑方式差别较大；对受剪尺寸效应机理存在不同认识，各计算公式中的尺寸效应因子存在较大差异。

实际工程中，结构转换层的实心厚板以及基础底板中有可能采用单向受力的无腹筋梁、板，而占据主流地位的有腹筋梁受剪承载力计算公式大多基于经典桁架模型，混凝土承担的剪力仍是计算公式的重要组成部分。因此，针对无腹筋梁剪切破坏机理及受剪承载力计算方法的研究工作仍然有重要的理论意义和工程背景。

本文对颇具代表性的无腹筋细长梁剪切破坏机理模型、相关试验成果及受剪承载力计算公式进行了介绍和评析，并基于大量试验数据对各理论模型的受剪承载力计算公式进行了评估分析。当剪跨比较小时，无腹筋梁通常发生混凝土抗压强度控制的斜压破坏，具有较大的受剪承载力，中等剪跨比梁则发生剪压破坏，另一方面，考虑到上述机理模型的适用范围，本文主要讨论剪跨比较大（≥2.5）的无腹筋细长梁的剪切破坏机理模型。

1 理论模型综述与评析

1.1 基于修正压力场理论（MCFT）的抗剪模型

多伦多大学的Vecchio和Collins教授在平衡桁架模型、协调桁架模型（压力场理论）的基础上提出修正压力场理论[3]，应用于钢筋混凝土剪扭构件的分析中。

基于修正压力场理论，Collins等[4-5]提出钢筋混凝土细长梁抗剪设计的一般方法，其中，混凝土的抗剪贡献项为Vc=βf′cbdv（图1），认为截面受压区混凝土不承担剪力，而梁腹混凝土的剪应力传递机制（参数β）为骨料咬合力并主要取决于斜裂缝宽度，当斜裂缝宽度增加时梁的受剪承载力将显著降低。计算模型中两个主要的参数是纵向受力钢筋的应变和裂缝间距。随纵筋应变增加，无腹筋梁的受剪承载力下降，称为纵筋应变效应；斜裂缝宽度直接影响骨料咬合力，Collins等人认为梁腹部的裂缝间距与梁的高度直接相关，尺寸较大的梁裂缝间距较大，由此引入尺寸效应。Collins等人提出的计算方法先后被加拿大CSA规范、美国AASHTO规范和CEB-FIP 2010模式规范采用。

基于修正压力场理论的抗剪模型忽略斜裂缝宽度沿斜裂缝面的变化，采用梁腹中部的裂缝宽度代表斜裂缝宽度。而魏巍巍等[6-7]认为对于发生剪切破坏的钢筋混凝土梁，由于存在弯矩，斜裂缝宽度沿截面高度方向发生变化，对骨料咬合力存在明显影响。基于以上分析，魏巍巍等对基于修正压力场理论的抗剪设计方法提出修正，在假定裂缝宽度沿截面线性变化的基础上建立了裂缝面平均剪应力计算公式及相应的受剪承载力简化计算公式。

1.2 临界剪切裂缝理论（CSCT）

瑞士学者Muttoni引用Leonhardt和Walther、Muttoni和Thürlimann的梁试验结果：当剪跨段未形成斜裂缝或者斜裂缝的宽度受到限制时，梁的极限承载力将显著提高，从而认为斜裂缝的形成与发展导致梁剪切破坏的发生，建立临界剪切裂缝理论[8]。

临界剪切裂缝理论结合不同受力阶段抗剪机制的改变对斜裂缝的形成与发展作如下解释：临界剪切裂缝形成前，剪力由悬臂作用、骨料咬合作用和销栓作用承担，当上述抗剪机制在弯曲裂缝尖端、裂缝与纵筋相交的局部位置产生的拉应力超过混凝土抗拉强度时，临界剪切裂缝形成，削弱了上述抗剪机制，此后由骨料咬合作用、肘形压杆复合形成拱效应作为新的抗剪机制。

在试验方面，Muttoni[9]采用精细方法测得斜裂缝面间的法向位移和切向位移，直接证明剪切破坏梁中骨料咬合作用的存在；Muttoni团队的Rodrigues[10]针对剪切对塑性铰转动能力的影响进行了试验研究，认为无腹筋梁、板可能在纵向钢筋屈服后，由于转动能力增加导致裂缝宽度增加，进而发生剪切破坏，将临界剪切裂缝理论进行了推广应用。

对应的受剪承载力计算方法认为无腹筋梁的受剪承载力取决于混凝土抗压强度的1/2次方及临界斜裂缝的宽度及粗糙度，定义距集中荷载作用点0.5d处为临界截面，由临界截面控制高度（距梁顶0.6d）处的纵向应变与截面有效高度的乘积代表临界剪切裂缝宽度，见图2，并假定该纵向应变可根据平截面假定计算。

1.3 塑性理论

20世纪70年代开始，丹麦学者Nielsen逐步建立了系统性的混凝土结构塑性分析理论。Nielsen团队的Zhang在塑性理论中引入裂缝滑移模型[11-12]，认为由斜向开裂转化形成的屈服线比未开裂区域的屈服线更为危险，梁的受剪承载力与裂缝面的滑移强度相关，并给出了确定裂缝面滑移强度以及临界斜裂缝位置的方法。

Zhang将发生滑移破坏的剪切破坏面定义为临界斜裂缝，引用Muttoni[9]测得的斜裂缝面间的相对位移解释屈服线的形成过程：临界斜裂缝形成时，相对位移垂直于裂缝发展方向，当裂缝面间产生切向位移时临界斜裂缝即转化形成屈服线。此后，由于骨料咬合作用的存在，裂缝面能够继续传递剪力，荷载增加使得斜裂缝继续发展，当裂缝面的剪应力超过混凝土的滑移强度时，沿屈服线产生滑移破坏，进而导致梁的剪切破坏。在抗剪机制层面，忽略了受压区、纵筋销栓作用对受剪承载力的贡献。

在确定裂缝面的滑移强度时，假定混凝土、钢筋均为刚塑性材料，裂缝面滑移强度服从修正的Mohr-Coulomb准则，屈服线及最终破坏面均为图3（a）所示直线，在考虑微观开裂、宏观裂缝对混凝土滑移强度的影响时，假定内摩擦角不变，引入强度有效系数对内聚力进行折减，进而实现对滑移强度的折减；在确定临界斜裂缝位置时，根据塑性理论将斜向开裂荷载和受剪承载力均表示为屈服线下端点距支座内边缘距离x的函数，如图3（b）所示，通过二者的等效关系计算x的值，进而求得梁的受剪承载力。

中国学者蒋大骅[13]认为Nielsen等人提出的塑性理论采用了理想化的应力场或者破坏机构，计算简图与实际破坏模式差别较大。陆勤等[14]人在经典塑性理论的基础上考虑靠近支座部分梁体转动，建立了新的破坏机构，并基于试验研究确定了混凝土强度塑性系数，提出了新的受剪承载力计算方法。

1.4 压力路径理论（CFPT）

希腊学者Kotsovos提出的压力路径理论[15]认为无腹筋梁跨中截面的压应力向支座传递形成压力路径。如图4所示，压力路径方向的改变、沿压力路径应力大小的变化、斜裂缝尖端位置、纵筋与混凝土的粘结破坏均可能在与压力路径垂直的方向产生拉应力，导致梁内压力路径失效，进而发生剪切破坏。

根据现有设计规范“临界截面”的概念，需在梁的整个剪跨段内配置适量腹筋以防止脆性剪切破坏发生。Kotsovos完成了仅在剪弯段局部区域配置箍筋的梁受剪试验[15]，表明对于不同剪跨比的梁，仅在可能出现拉应力的局部区域配置箍筋就能够防止发生剪切破坏，该试验结果成为直接支持压力路径理论的证据，且对临界截面、骨料咬合作用等传统概念提出质疑。在研究纵筋销栓作用时，设计以钢筋直径为试验变量的梁受剪试验，结果表明在钢筋面积不变而直径变化时，梁受剪承载力并无明显变化，因此认为纵筋销栓作用对无腹筋梁受剪的贡献可以忽略[16]。

在计算方面，Kotsovos仅对Bobrowski等[17]经验公式提出了修正，但是其“仅在可能出现拉应力的区域配置箍筋就能防止剪切破坏的发生”的抗剪设计思想却值得关注。

刘立新[18]在桁架模型中考虑了拱效应（压力路径），认为桁架拱模型能够反映不同剪跨比梁的破坏机理，并引用双向应力状态下的混凝土强度破坏准则，建立了适用于不同剪跨比的无腹筋梁受剪承载力统一计算方法。史庆轩等[19]基于桁架拱模型，建立了考虑混凝土的软化效应、拱效应的受剪承载力公式。

1.5 劈裂破坏理论

希腊学者Zararis基于对钢筋混凝土薄膜元的受力分析，对钢筋销栓作用、骨料咬合作用的机理提出不同观点[20]：与裂缝垂直方向上的应力为拉应力而非压应力，因此骨料咬合作用的本质并非摩擦力；裂缝面的钢筋承担剪力是由于纯剪切变形，并非由于弯折或者沿裂缝面的相对滑移。基于上述分析，Zararis[21]假设裂缝张开方向与发展方向垂直，即忽略裂缝面的相对滑移，裂缝面上仅存在钢筋的法向力和切向力，认为无腹筋细长梁剪切破坏的实质是剪跨段局部区域的混凝土劈裂破坏。

通过分析剪切破坏梁的裂缝特征，假定剪切破坏面由两段分支组成：第一分支为近似直线的斜剪切裂缝，高度与弯曲裂缝一致，在靠近支座的弯曲裂缝尖端或者弯曲裂缝之间形成；第二分支位于由加载点指向支座的压力线上，由第一分支上端点突然或者逐渐穿过受压区向加载点发展，沿第二分支发生混凝土劈裂破坏。通过内力分析确定了裂缝第一分支的高度、倾角以及第一分支下端距支座的距离，得到图5（a）所示的最终破坏面示意图。在分析局部应力分布时，取图5（b）所示隔离体，假定裂缝第二分支上仅存在法向应力，考虑受压边界条件，在两对作用力产生的应力分布上叠加常拉应力项，得到5图（c）所示应力分布，当裂缝第一分支上端点（D点）的拉应力超过混凝土劈裂抗拉强度时，形成裂缝第二分支并导致最终破坏。并认为梁受剪尺寸效应的本质是混凝土圆柱体劈裂破坏的尺寸效应，引用Hasegawa[22]的试验结果，提出与梁截面有效高度、剪跨比相关的尺寸因子。

劈裂破坏理论认为无腹筋细长梁的受剪承载力主要取决于混凝土劈裂抗拉强度和受纵向配筋率、混凝土抗压强度影响的混凝土受压区高度。

1.6 基于截面应变分析的抗剪模型

基于截面应变分析的抗剪模型[23]由韩国学者Park-Choi提出，认为无腹筋细长梁发生破坏时，斜拉裂缝穿过整个受压区，为斜拉破坏。同时，认为裂缝间的残余拉应力、骨料咬合作用、纵筋销栓作用（单排布置钢筋）对抗剪的贡献均可以忽略。

假定受压区的应力状态服从图6（a）所示的Rankine强度准则，当主应力超过混凝土的抗压或者抗拉强度时发生破坏，对于无腹筋细长梁而言，由抗拉强度控制的受剪承载力明显低于由抗压强度控制的受剪承载力。截面的许用剪应力与法向压应力大小有关，法向压应力的大小及分布则受到截面的弯曲变形（曲率）和受拉钢筋的抗拉强度影响，在建立截面应变分析模型时，假设破坏面GH与截面GG的抗剪承载力相等，见图6（b），选取法向压应变αε0表征截面的弯曲变形，c（αε0）表示对应截面的受压区高度，由许用剪应力沿截面受压区高度积分得到梁的受剪承载力。并直接引用了Zararis等[22]提出的尺寸效应因子。

王景全等[24]认为基于截面应变分析的抗剪模型中用于描述剪压区混凝土应力状态的Rankine强度准则过于复杂，简化后可偏安全的取ft=0.07f′c，分别得到受剪承载力由混凝土抗拉、抗压强度控制的简化强度准则，并建立了形式简单的梁受剪承载力统一计算公式。吕艳梅[25]放弃了Park-Choi模型中的纵向应变平截面假定，并采用修正的Ottosen强度准则（更适用于高强混凝土）描述剪压区的混凝土应力状态，对该模型进行了修正。于磊[26]直接引用Zararis提出的受压区高度求解方法及尺寸效应因子对Park-Choi模型中的受压区高度计算方法进行了简化。

1.7 理论模型评析

从概念上看，Kotsovos的观点无疑是正确的。集中荷载作用点到支座之间的确存在一条压力路径，很早以前的“拱齿模型”[27]直接就用拱的传力描述这条路径。但Kotsovos没有清楚的说明这条压力路径的失效机理。换一个角度，可以认为Kotsovos持有无腹筋梁剪切破坏就是剪弯区段梁腹部混凝土受拉破坏的观点。Collins等人提出的抗剪模型，完全忽略截面受压区混凝土承担的剪力，无腹筋梁的剪力几乎全部由骨料咬合力传递。虽然修正压力场理论已经成为解释钢筋混凝土薄膜单元受力性能的主流观点，但该理论应用于钢筋混凝土无腹筋梁抗剪问题时，实际上只用到MCFT中偏于经验的那一部分，即混凝土开裂后在应力主方向上由骨料咬合作用传递的剪力。Muttoni的模型（CSCT）与Collins的模型在原理上有一些相似，也认为骨料咬合作用是主要的传力机制，临界剪切裂缝成为剪切破坏的主要特征，但Muttoni至少没有在概念上否定复合压杆传递的剪力。Muttoni引用εd/（16+dg）作为主要变量（其中d为截面有效高度，ε为距受压边缘0.6d处的应变，εd就是临界剪切裂缝宽度，dg为最大骨料粒径），这也与Collins的公式有几分相似。对剪跨比较大的无腹筋梁，Zararis的模型主要来源于试验观察，认为斜裂缝由第一分支到第二分支的转折是由于梁腹部的混凝土劈裂受拉破坏。这在机理上就与Collins及Muttoni的模型完全不同。持有相近观点的还有Park-Choi等人，他们认为斜裂缝一直延伸并穿越截面受压区，但他们没有去计算斜裂缝上混凝土的受拉或受剪破坏，而是将其转化为临界状态时混凝土受压区在复合应力作用下的破坏。Zhang的模型基于塑性理论，认为我们看到的斜裂缝是沿屈服线的剪切滑移破坏。从机理上看，如果无腹筋梁的剪切破坏可以认为是一种特殊的塑性破坏，而且破坏面（屈服线）由临界斜裂缝决定，沿破坏面上的剪切滑移抗力也应该主要由骨料咬合力提供。

由此看来，对于无腹筋细长梁，上述所有抗剪模型都不认可截面受压区混凝土承担的剪力对抗剪承载力的贡献，同时也都没有考虑纵筋的销栓作用。梁腹混凝土的受拉（劈裂）或受剪（骨料咬合）成为抗剪机制的主要分歧。

Muttoni等[9]采用较为细致的试验数据证明临界剪切裂缝两侧存在相对滑移，由此说明骨料咬合作用对抗剪的贡献。Collins等[28]用不同骨料粒径的无腹筋梁受剪试验说明其受剪承载力在一定范围内随最大骨料粒径变化。Zararis从斜裂缝的两个分支推断，导致斜拉破坏的斜裂缝第二分支源于混凝土劈裂受拉破坏。总的来看，直接的试验支持都不是十分充分。

应当指出，在分析推导层面，基于截面应变分析的Park-Choi抗剪模型忽略了其他抗剪因素，认为受压区混凝土承担剪力和压力，并假定压应力和剪应力的共同作用服从Rankine强度准则，最后的结果是混凝土主拉应力控制剪切破坏。虽然推演的结果与试验数据颇为接近，但图6中所示的破坏发生GH斜截面，GH斜截面上的斜拉破坏与GG面上混凝土主拉应力控制的破坏的关系不明确，机理上的缺陷非常明显。

在受剪尺寸效应方面，基于修正压力场理论的抗剪模型和临界剪切裂缝理论都认为尺寸效应是由于截面有效高度增加导致斜裂缝宽度增加，骨料咬合作用降低；塑性理论在混凝土强度有效系数中间接考虑了梁截面有效高度的影响；压力路径理论并未考虑无腹筋梁的受剪尺寸效应；而Zararis认为受剪尺寸效应的本质是混凝土劈裂破坏的尺寸效应，建议采用与截面有效高度、剪跨比有关的尺寸因子；基于截面应变分析的抗剪模型则直接引用了Zararis尺寸效应因子。

2 受剪承载力计算公式

不同理论模型对剪切破坏机理和影响因素的认识的区别与联系在受剪承载力计算公式中均有所体现，见表1。在计算步骤及公式形式层面，MCFT简化公式和CSCT公式均需进行多次迭代求解，劈裂破坏理论公式需求解一元二次方程，Park-Choi简化公式和塑性理论公式的计算公式较为复杂且限制条件较多。

3 受剪承载力计算公式评估

3.1 设计参数影响评估

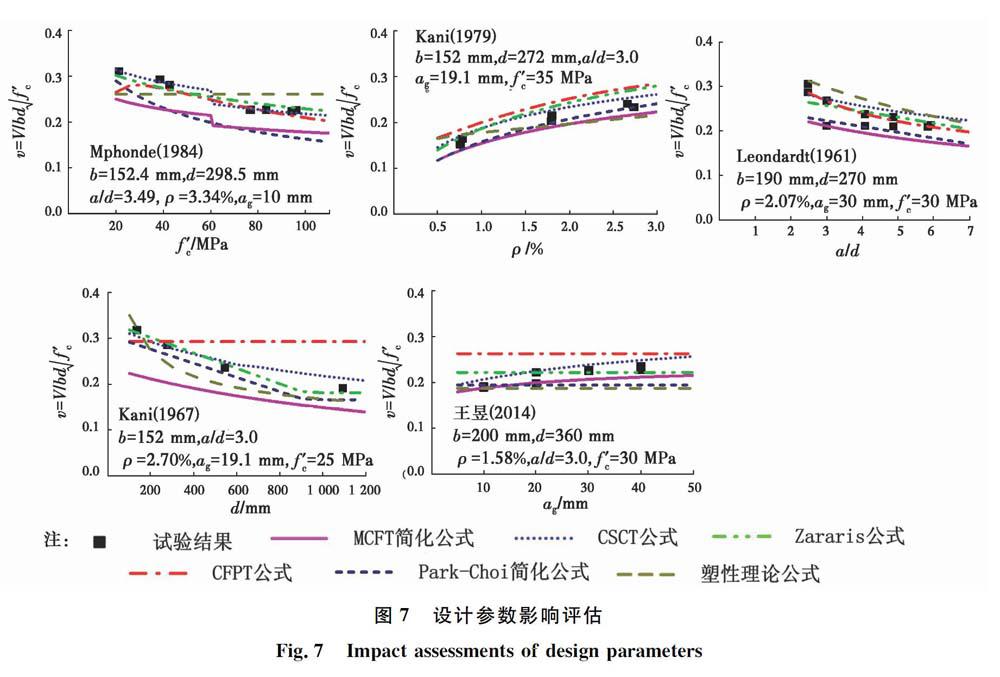
由于无腹筋梁剪切破坏的影响因素众多，各影响因素之间的相互作用机理难以确定，而基于变量分离思想进行的试验应该能够反映不同影响因素对梁受剪承载力的影响。为评估上述计算公式的设计参数的合理性，分别选择Mphone[30]、Kani[31]、Leonhardt[32]、易伟建等[33]的试验结果进行评估分析。

图7结果表明现有理论模型的受剪承载力计算公式基本能够反映各影响因素对梁受剪承载力的影响，但是仍存在不同程度的缺陷：塑性理论公式无法反映受剪承载力与混凝土强度增长之间的非比例关系；

CFPT公式明显未考虑尺寸效应，且当截面有效高度大于一定程度后，Zararis公式与Park-Choi简化公式均无法反映梁受剪的尺寸效应；最大骨料粒径对梁受剪承载力的影响在Zararis公式、CFPT公式和Park-Choi简化公式中均不能体现。总之，上述理论模型的受剪承载力计算公式均存在不同程度的局限性，对各影响因素对受剪承载力的影响并未形成统一的认识。

3.2 统计方法评估

基于Reineck等人[34]建立的ACI-DAfStb剪切破坏数据库，筛除非矩形截面梁、剪跨比小于2.5、最大骨料粒径信息不完整的部分试验数据，得到包含586个试验结果的数据库：13.34 MPa≤f′c≤139.0 MPa，0.14%≤ρ≤6.64%，2.50≤a/d≤8.10，65 mm≤d≤2 000 mm，采用表1所示的计算公式进行分析。

图8的结果表明：总的来看，试验值与计算值比值的变异系数约为20%，其中，MCFT简化公式和CSCT公式的偏差较小，但MCFT简化公式所得结果的平均值较大，从图8（a）可以看到数据比较分散，计算精度最高的应属CSCT公式。按照统计学的观点，可以认为偏差较小的计算模型更加真实地反映了对象的特征。一个有意思的现象是计算精度较差且明显偏于不安全的CFPT公式（压力路径理论）对剪跨比这个因素的预测具有较好的精度，说明不同计算模型具有不同的特点。需要指出的是以剪跨比2.5区分细长梁和短梁，是根据Kani的剪切破坏谷做出的划分。教科书上对剪切破坏做出斜压破坏、剪压破坏和斜拉破坏的描述，对应的剪跨比实际上没有明确的界限。而剪压破坏和斜拉破坏的共同之处，就是斜截面破坏都发生在临界斜裂缝。另一个需要说明的问题是，文中对基于机理模型的受剪承载力理论计算公式进行评估，给出了试验值与计算值比值的平均值和变异系数。但是在于工程设计应用中，需要根据统计平均值和变异系数，对上述理论公式的相关系数进行调整，以满足结构可靠性要求。

4 存在的问题和研究展望

MCFT和CSCT都认为沿斜裂缝的骨料咬合力是无腹筋梁受剪的主要机制，但CFPT和Park-Choi模型关注截面受压区传递的剪力；塑性理论似乎过于理想化，Zararis的劈裂计算模式对临界斜裂缝的驱动力假设也与试验观察不完全相符。每一种理论模式都找到了一些试验现象和数据的支持，但又与另一些试验现象和数据矛盾，这使我们不得不重新审视数以千计的试验数据本身。几十年前，Zsutty率先采用全统计方法得到的公式至今仍保持了相对较高的精度[35]，说明问题的随机属性在一定程度上掩盖了问题的物理属性。进一步的研究需要运用概率论的方法研究以临界斜裂缝为特征的概率密度演化和主要随机变量的影响。

计算理论的突破仍依赖于试验。虽然Muttoni等[9]仔细测量了临界斜裂缝的张开和相对滑移。稳定扩展的临界斜裂缝可以测量相关数据，但突然出现的斜拉裂缝似乎更接近Zararis描述的劈裂破坏。最近，王昱用高速摄像机捕捉到斜拉裂缝的生成也不支持临界裂缝稳定扩展的假设[36]。借助高速数字图像相关技术也许可以动态扑捉临界斜裂缝的扩展和相对位移，理论上这种技术还可以得到应变分布的动态变化，有助于对破坏机理的认识。

实际工程多为有腹筋梁，腹筋的加入将使梁的破坏机理发生明显的变化。工程设计中很多规范公式用混凝土承担的剪力加上腹筋承担的剪力表示有腹筋梁的受剪承载力，并且根据无腹筋梁的试验研究确定混凝土承担的剪力。大多数有腹筋梁的受剪承载力计算公式实际上隐含了混凝土承担的剪力不随腹筋加入而变化的假设。但这只是设计公式的简化，并不表示真实的抗剪机理，还有进一步研究的空间。

5 结 论

对具有代表性的无腹筋细长梁剪切破坏理论模型、中国相关研究及受剪承载力计算公式进行了介绍和评述，得到以下结论：

1）现有抗剪机理模型对无腹筋细长梁的剪切破坏机理尚未形成共识，主流抗剪机理模型（以MCFT和CSCT为代表）不认可截面受压区混凝土承担的剪力对受剪承载力的贡献，同时也都没有考虑纵筋的销栓作用。梁腹混凝土的受拉（劈裂）或受剪（骨料咬合）以及受压区混凝土承担的剪力成为抗剪机制的主要分歧。

2）现有理论模型对于无腹筋细长梁受剪尺寸效应的根本原因的认知并不统一，国内外关于大尺寸梁受剪破坏的试验研究成果依旧不够丰富，实际工程中配筋率较低的无腹筋厚板可能存在安全隐患，应给予充分重视。

3）不同理论模型的受剪承载力计算公式对不同影响因素的考虑方式存在较大差异，其合理性有待商榷。已有的试验数据较为分散，导致问题的随机特性在一定程度上掩盖了问题的物理属性。深入研究应从考虑主要随机变量影响的概率密度演化着手，利用先进测试技术获取试验信息，进一步揭示剪切破坏的内在机理。

4）围绕钢筋混凝土无腹细长梁剪切破坏机理的研究仍存在较大理论意义和工程背景，混凝土结构理论的结构物理学特征也敦促研究人员寻求本质层面的剪切破坏机理，不断发展的动态测试技术、图像分析方法和非线性有限元方法将推动相关问题的研究。

参考文献：

[1] ANDERSON B G. Rigid frame failures [J].ACI Journal Proceedings， 1957， 53（1）：625-626.

[2] RAMIREZ J A， FRENCH C W， ADEBAR P E， et al. Recent approaches to shear design of structural concrete [J]. Journal of Structural Engineering， 1998， 124（12）： 1395-1396.

[3] VECCHIO F J， COLLINS M P. The modified compression-field theory for reinforced concrete elements subjected to shear [J]. ACI Journal Proceedings， 1986， 83（2）：219-231.

[4] BENTZ E C， COLLINS M P. Development of the 2004 Canadian Standards Association （CSA） A23. 3 shear provisions for reinforced concrete [J]. Canadian Journal of Civil Engineering， 2006， 33（5）： 521-534.

[5] COLLINS M P， MITCHELL D， ADEBAR P，et al. A general shear design method [J]. ACI Structural Journal， 1996，93（1）： 36-41.

[6] 魏巍巍， 贡金鑫， 车轶. 无腹筋钢筋混凝土受弯构件基于修正压力场理论的受剪计算[J]. 建筑结构学报， 2010， 31（8）： 79-85.

WEI W W， GONG J X， CHE Y. Shear strength of reinforced concrete members without stirrups based on modified compression field theory [J]. Journal of Building Structures， 2010， 31（8）： 79-85.（in Chinese）

[7] WEI W W， CHE Y， GONG J X. Shear strength prediction for reinforced concrete beams without stirrups [J]. Magazine of Concrete Research， 2011， 63（6）： 433-440.

[8] MUTTONI A， RUIZ M F. Shear strength of members without transverse reinforcement as function of critical shear crack width [J]. ACI Structural Journal， 2008， 105（2）： 163-173.

[9] MUTTONI A， THRLIMANN B. Shear tests on beams and slabs without shear reinforcement [J]， Institut für Baustatik und Konstruktion， Zürich， Switzerland， 1986： 1-12 .

[10] RODRIGUES R V， MUTTONI A， RUIZ M F. Influence of shear on rotation capacity of reinforced concrete members without shear reinforcement [J]. ACI Structural Journal， 2010， 107（5）：516-517.

[11] HOANG L C， NIELSEN M P. Plasticity approach to shear design [J]. Cement and Concrete Composites， 1998， 20（6）： 437-453.

[12] ZHANG J P. Diagonal cracking and shear strength of reinforced concrete beams [J]. Magazine of Concrete Research， 1997， 49（178）： 55-65.

[13] 蒋大骅. 钢筋混凝土梁抗剪强度的塑性解[J]. 同济大学学报：自然科学版， 1979， 5：29-43.

JIANG D H. Plastic solution for the shear strength of reinforced concrete beam [J]. Journal of Tongji University： Natural Science， 1979， 5： 002. （in Chinese）

[14] 陆勤， 蒋永生， 丁大钧. 按塑性理论计算矩形截面钢筋混凝土简支梁的抗剪强度[J]. 南京工学院学报， 1988，18（1）：23-29.

LU Q， JIANG Y S， DING D J. Plastic theory based calculation method for the shear strength of rectangular section reinforced concrete simply supported beam [J]. Journal of Nan Jing Institute of Technology， 1988，18（1）Ⅱ.23-29. （in Chinese）

[15] KOTSOVOS M D. Compressive force path concept： basis for reinforced concrete ultimate limit state design [J]. ACI Structural Journal， 1988， 85（1）：68-76.

[16] JELI I， PAVLOVI M N， KOTSOVOS M D. A study of dowel action in reinforced concrete beams [J]. Magazine of Concrete Research， 1999， 51（2）： 131-135.

[17] BOBROWSKI J， BARDHAN-ROY B K. A method of calculating the ultimate strength of reinforced and prestressed concrete beams in combined flexure and shear [J]. The Structural Engineer， 1969， 47（5）： 197-198.

[18] 刘立新. 钢筋混凝土深梁， 短梁和浅梁受剪承载力的统一计算方法[J]. 建筑结构学报， 1995， 16（4）： 13-21.

LIU L X. Unified calculation method for the shear capacity of reinforced concrete deep， short and slender beams [J]. Journal of Building Structures， 1995， 16（4）： 13-21. （in Chinese）

[19] 史庆轩， 王朋， 王秋维. 桁架拱模型用于钢筋混凝土梁的受剪承载力计算分析[J]. 土木建筑与环境工程， 2013， 35（4）： 7-12.

SHI Q X， WANG P， WANG Q W. Shear capacity calculation analysis of reinforced concrete beams based on truss-arch model [J]. Journal of Civil， Architectural & Environmental Engineering， 2013， 35（4）： 7-12. （in Chinese）

[20] ZARARIS P D. Aggregate interlock and steel shear forces in the analysis of RC membrane elements [J]. Journal of Structural Engineering， 1997， 94（2）： 159-161.

[21] ZARARIS P D， PAPADAKIS G C. Diagonal shear failure and size effect in RC beams without web reinforcement [J]. Journal of Structural Engineering， 2001， 127（7）： 733-742.

[22] HASEGAWA T， SHIOYA T， OKADA T. Size effect on splitting tensile strength of concrete [C]// Proceedings Japan Concrete Institute 7th Conference， 1985： 309-312.

[23] PARK H G， CHOI K K， WIGHT J K. Strain-based shear strength model for slender beams without web reinforcement [J]. ACI structural Journal， 2006， 103（6）： 783-793.

[24] 王景全， 戚家南. 有腹筋与无腹筋钢筋混凝土梁抗剪承载力统一计算方法[J]. 土木工程学报， 2013， 46（7）： 47-57.

WANG J Q， QI J N. Unified shear strength computation model for reinforced concrete beams with and without stirrups [J]. China Civil Engineering Journal， 2013， 46（7）： 47-57. （in Chinese）

[25] 吕艳梅. 高强箍筋高强混凝土梁抗剪性能试验研究与理论分析[D]. 长沙：湖南大学， 2008.

LV Y M. Theoretical and experimental research on shear capacity of high strength beams with high strength stirrups [D]. Changsha： Hunan University， 2008. （in Chinese）

[26] 于磊. 大尺寸钢筋混凝土梁受剪试验研究[D]. 大连：大连理工大学， 2013.

YU L. Experimental investigation on shear strength of large size reinforced concrete beams [D]， Dalian： Dalian University of Technology， 2013.（in Chinese）

[27] FENWICK R C， PAULAY T. Mechanisms of shear resistance of concrete beams [J]. Journal of the Structural Division， 1968.94（ST10）： 2235-2343.

[28] SHERWOOD E G， BENTZ E C， COLLINS M P. Effect of aggregate size on beam-shear strength of thick slabs [J]. ACI Structural Journal， 2007， 104（2）：188-183.

[29] CHOI K K， PARK H G， WIGHT J K. Unified shear strength model for reinforced concrete beams-Part I： development [J]. ACI Structural Journal， 2007， 104（2）：142-152.

[30] MPHONDE A G， FRANTZ G C. Shear tests of high-and low-strength concrete beams without stirrups [J].ACI Journal Proceedings， 1984， 81（4）： 350-355.

[31] KANI G. Kani on shear in reinforced concrete [M]. Department of Civil Engineering， University of Toronto， 1979.

[32] LEONHARDT F， WALTHER R. The stuttgart shear tests， 1961[M]. London： Cement and Concrete Association， 1964.

[33] 易伟建， 王昱， 邓清. 骨料粒径对无腹筋梁抗剪性能影响的试验研究[J]. 湖南大学学报（自然科学版）， 2014， 41（11）： 1-5.

YI W J， WANG Y， DENG Q. Experimental study on aggregate size role in shear strength of reinforced concrete beams without shear reinforcement [J]. Journal of Hunan University （Natural Sciences）， 2014， 41（11）： 1-5. （in Chinese）

[34] REINECK K H， BENTZ E C， FITIK B， et al. ACI-DAfStb database of shear tests on slender reinforced concrete beams without stirrups [J]. ACI Structural Journal， 2013， 110（5）： 867-875.

[35] ZSUTTY T C. Beam shear strength prediction by analysis of existing data [J]. ACI journal proceedings， 1968， 65（11）： 943-949.

[36] 王昱.骨料粒径对无腹筋梁抗剪性能影响的试验研究[D].长沙：湖南大学， 2014.

WANG Y. Experimental study on aggregate size role in shear strength of reinforced concrete beams without shear reinforcement [D].Changsha： Hunan University， 2014. （in Chinese）

（编辑 胡玲）