中学数学教师学科知识发展对“二级思维跳跃模式”的积极影响
2016-11-30彭艳贵
彭艳贵
(鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)
中学数学教师学科知识发展对“二级思维跳跃模式”的积极影响
彭艳贵
(鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)
在大学期间的数学课程中学到的知识对教师后继的发展是有积极意义的,尽管其在教师的教学过程中无法以外在的形式直接发挥作用,但在教师对教学内容的判断、处理,数学思想方法的把握,以及教学内容结构的理解等方面发挥着至关重要的作用.特别是,大学中的专业课程学习使得学习者在思维层次上呈现出一种“二级思维跳跃”的特点,这对教师入职前的学科知识发展起到至关重要的作用.
中学数学教师;大学数学课程;学科知识发展;统摄程度
随着数学学科本身的发展和数学教育水平的不断提高,高等数学知识越来越多地渗透或下移到中学数学课程内容之中.然而,随着数学教育水平的发展,一直存在两种普遍的、对立的观点.经过对中学教师观念的实际调查发现,有的教师认为中学数学教师学习大学中的数学专业课程没有用处,甚至有人认为随着教师职业工作经验的增加,只要掌握所教的中学数学课程本身所包含的知识内容就行了;相反的,有的数学教师认为在大学曾经学过的数学专业课程中的知识对自己的中学数学教学起到了积极的作用.教育部即将推行教师资格考试制度的改革,教师资格考试的内容的一部分就是学科知识.数学学科知识是数学教学知识的基础,只有正确、深刻理解数学学科知识,才有可能从根本上充分结合教学主体、教学方法、教学手段、教学环境等众多因素把中学数学课程中的内容以一种易于理解的表现形式呈现出来,帮助学生实现知识的内化和认知系统的建构,本质上也是对学习过程中的数学知识的一种压缩和融合.
在提到教师的培养和发展时,通常是以教师的教学能力为核心.有研究者指出,根据教师在教学活动中的主要行为,可以将教师教学能力划分为“教学设计能力”“教学实施能力”和“教学监控能力”3个维度[1].1986年,随着美国著名学者舒尔曼(shulman)给出“学科知识”的概念以来,人们开始认为教师的学科知识是对学生的学习产生影响的决定性因素[2].而教师在大学期间曾经学过的数学专业课程中的知识作为舒尔曼提出的“学科知识”概念当中发挥作用的一种重要成分,对这3种教学能力有什么样的影响呢?影响又是否相同?这3种教学能力的发展是否完全依赖教师资历的加深?或者是完全依赖教师的包含大学数学专业知识在内的比较稳定的学科知识结构?这些问题是当今教师培养和发展的核心问题,很值得研究和讨论.
1 学科知识发展的“二级思维跳跃模式”
数学是抽象的,按照认知主义观点,数学学习实质上是学习者通过数学活动的认识过程,凭借已有的“数学现实”,使得知识成为可以在思维结构中操作的对象,这个过程从知识接受程度来说是数学知识在学习者认知结构中的表示形式从相对具体到相对抽象的过程,同样也可以看成是学习者的思维从相对低级到相对高级的一种变化,正是这样一种变化使得人们相信“数学是思维的体操”.逐级抽象是数学知识发展的一个特点,数学学习的过程正是由无数个像这样相对较小的、从具体到抽象的思维变化过程,学习者逐渐获得更加抽象的数学知识,形成统摄程度更高的数学概念,逐渐达到相对的、阶段性的数学学习的目标.按照中学数学教学对教师的要求,教师无论是在知识上,还是在思维层次上都应该达到一定的标准.通常情况下,大学数学专业相对基础一些的课程的学习在知识的统摄性程度、综合性程度、思想方法、技巧和策略等方面可以看成是从初等数学到一般高等数学的第一级思维跳跃过程.大学数学专业后续的、更加抽象些的课程的学习可以看作是对之前所学知识和内容的再一次升华,即从一般的高等数学基础知识到高级数学的第二级思维跳跃过程.从中学数学教师的学科知识发展的角度来说,个人的数学学习经历二级跳跃式思维抽象过程是很有意义的.
1.1 第一级思维跳跃
把数学分析、高等代数等大学数学专业的基础课程学习看作是在知识的统摄性程度、综合性程度、思想方法、技巧和策略等方面从初等数学到一般高等数学的第一级思维跳跃.例如,大学时在学习数学分析课程中,要掌握讨论函数性质的无穷小方法,从微分与积分的互逆关系上看到数学对象间有机的联系,从数学分析知识结构上获得数学理论的构建方法,更要在每一个数学概念、命题的学习过程中领悟数学家从事数学活动研究数学问题的思维方式方法.特别是,以教师为职业目标的大学生应主动思考这些问题:数学分析研究的对象是什么?研究的方法是什么?如何展开研究?获得了哪些结果?一个学生只有在思想方法层面理解知识,在直观水平上理解知识,才能形成迁移到中学数学教学中的能力,否则,光知道一些名词术语,记住一些计算用的法则与方法是难以在新的场合运用的.高师生还要重视学习积累关于解决中学数学问题常用的数学思想方法,如数形结合、转化与化归、函数与方程、分类讨论、几何变换、模型法、待定系数法,等等.
再如,关于函数的数学知识在近代数学中得到系统的发展,不论在解决实际问题中,还是在数学本身,都是至关重要的内容.函数概念贯穿初中数学、高中数学直至大学数学,一直都是数学学习的主要内容.初中数学中主要是使学生在宏观上认识函数的概念和简单的函数类型(一次函数、反比例函数和二次函数),高中数学中主要是借助映射概念在对应关系方面初步讨论函数的概念和性质,而在大学的数学分析课程中,以具体函数为对象进行极限、连续、求导、微分、积分等及其相关应用讨论,结构上更加系统,完全能够统摄中学的函数知识内容,学过了数学分析课程之后对函数概念的认识也必将上升到一个新的认识层次.
请看下面两个关于儿童数学学习的例子.
例1 4+( )<12,( )中最大填多少?
这是一个小学一年级的问题,要是填写4+( )=12,多数儿童可以很容易得出结果.对于这个阶段的学生来说,“<”比“=”的问题要困难一些,毕竟这个问题的答案是一类数,而不是某一个确定的数,并且这个问题已经是两类问题的综合,对儿童的思维是有一定挑战性.一位曾经受过基本加减法运算训练的儿童在计算这个问题之前,可以很容易算出4+(8)=12,但思考这个例子中关于“小于”的问题时还是感到很困难,不知道该如何判断.在判断过程中,儿童能够知道4+(1)=5小于12,4+(5)=9小于12,但还不能很容易的理解对于4+( )<12来说,只要在括号中填上小于8的数就符合要求,即固定加数4之后,按照加数递增的顺序依次验证符合要求的数字,再从0,1,2,3,4,5,6,7这些数字中找出最大的一个,或者按照验证的顺序直接找到最大的数字.
例2 5+( )>17,( )中最小填多少?
比前一个问题的回答直接一些,稍微思考,儿童即可很容易的说出括号中可以填写18,这位儿童解释说,因为18大于17,再加上5一定大于17而满足要求.对于小于17的数就需要加法运算进行判断了,但是仍然是随机选取0~17之间的数字进行验证的办法,如5+8=13小于17,之后再一次随机选取而不是按照顺序5+10=15小于17,直到想到5+11=16,再反复比较各个式子确定结果为止.
在上面两个关于儿童数学学习的例子中,教师应该如何看待儿童的学习过程呢?那就需要教师具有相应的学科知识和教学知识等,而不是仅仅靠资历或经验.若教师已经掌握了统摄程度更高的数系理论,能够借助自然数的序数特点来解释儿童的解题过程,对教师的教学指导是有积极意义的.再能够借助直观的例子帮助儿童建立正确的概念表象,理解自然数的基数理论和序数理论概念.
1.2 第二级思维跳跃
通过大学本科数学专业中各门基础课程的学习,形成一定的高等数学知识储备,进一步丰富了数学思想、方法、技巧等内容,锻炼了个人在复杂的数学思维环境中的适应能力,以此为基础,再把泛函分析等被认为大学本科阶段比较难学的课程学习看作是对之前所学知识和内容的再一次升华,即从一般的高等数学基础知识到高级数学的第二级思维跳跃.
如前所述,如果说函数概念在数学分析中的学习系统,统摄程度已经比较高了,那么在泛函分析这样的课程中,函数概念已经进一步地得到抽象,如之前学习过程中遇到的映射,在泛函分析课程中一般化为算子;之前讨论的函数以数为变量,在泛函分析中已经把函数一般化为变量;高等代数中的内积概念在泛函分析中也一般化为共轭双线性函数,相关知识的抽象程度和概念系统的统摄程度都很高,当然在思维训练的复杂程度方面也不可同日而语了.
数学概念甚至其它的数学知识的抽象与具体是相对的,因为数学知识具有逐级抽象的特点,而概括和推广是数学学习的一种重要方式.如度量概念的认识,泛函分析课程内容的一个重要特点是讨论无穷维空间上的问题,需要借助极限的手段,要定义极限进一步需要距离的概念.即可以写成如下链条:“泛函分析课程内容↔无穷维空间问题↔需要定义极限↔需要度量”.泛函分析中的空间概念可以看成是基本的集合概念赋以一定的“结构”.这是一种整体性的认识,是一种使得学习者思维层次得以升华的新的认识.如华东师范大学的李士琦老师论述“数学教学中的整体观念” 时所提到的那样,“数学整体的组成形式和它的相对独立性,使得总体的把握研究,往往要利用或提出一个新的数学概念,以它作为整体组织的手段或是整合的法则[3]”.再如度量空间的完备,为了理解完备概念,可以借助相对直观的一维或二维等已经熟悉的、简单的例子作为模型:
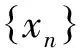
最后一个概念显然起到了知识整合的作用.具体的例子当中,距离的定义方式不同,对应的空间结构也不同了.在这个意义上,对于简单的一维和二维的情况,学习者也可以认识到距离的定义方式也可以不是唯一的了,打破了原有观念的束缚,这不能不说是学习者在思维层次上的认识上升到了新的高度.如果简单地概括而得出“合格的高中数学教师应该具备一定的类似于泛函分析课程的知识或者相应的思维层次”这样的结论,那就太武断了.但反过来,具备了类似于泛函分析课程的知识或者相应的思维层析能够更加有利于高中数学教学还是能够被信服的.在此也表明,关于中学数学教师的学科知识发展的含义、深度和广度等内容仍然是数学教育研究领域的一项重要内容.
1.3 心理学解释
按照认知心理学的观点,同化和顺应是数学学习过程中认知建构的基本形式.有教育研究者认为,在数学学习中.顺应比较多,所以数学难学.而通常情况下,教师掌握的数学知识程度越高,应用和处理数学内容的意识就越强,关于数学应用与教学的自信心也越强.对于教师在教学过程中遇到的学科知识来说,教师不一定需要创造数学知识,但是在教学过程中,教师需要创造对所教数学知识的理解,同时也会遇到教育改革中不断变化的数学教学内容,都是一个数学学习过程.当教师掌握比较多的大学数学课程知识的时候,教学过程中的学习同化就比较多、顺应比较少;而大学数学课程知识掌握相对比较少的时候,教学过程中的学习同化就会比较少,顺应比较多.比如,中学数学中的整数,若清楚抽象代数课程中的群、环、域等数学结构,把整数看成一个整体来认识,那么教师若想在中学数学教学中创造出一种易于学生接受的关于整数教学的理解,就好比在自己家里摆设家具一样,不论在整体上还是在单个物件上都会条理清楚.若不然,每一个整数在不同的问题中都是教师处理的直接对象,错综复杂,遇到复杂一些的情况必然难以妥善处理.再如,现代数学中提倡的公理化方法是对普通数学知识高度抽象概括出来的结果,在思想、方法和结构等方面带有普遍性的指导意义.这也是一种培养优秀数学教师,使其具备良好的学科知识基础和发展潜力的有效方式.
2 结语
中学数学教师通过大学期间数学专业知识的学习,具备了对数学学科的整体性认识,掌握了处理中学数学教学相关问题的高度抽象化的一般方法,具有了继续学习和深度思考中学数学内容的能力与信心等.东北师范大学的张凯军老师在谈论教师的培养时说,“人才培养模式的基点是强化教师专业职能,因此,大学过程中的教师教育应该在不低于本科基础水平前提下进行制度调整,教师教育方面仍应继续注重对教师学科基础知识的培养,在保证学科基础知识课程的基础上,尽量增加与数学教学知识相关的课程设置[4]”.目前,我国的数学教育界在学科知识方面要求中学数学教师具备一定的大学数学专业中的知识已经是一种共识,也已有一些师范大学对教师的培养进行相关改革,但在具体内容、方法和要求等方面,还没有制定出详细的学科知识标准,还需要进一步探索.因此,作为教育发展过程中的重要环节——教师的培养与发展,探索教师培养过程中的数学学科知识发展水平,制定科学、规范的中学数学教师学科知识发展标准,对数学教育的发展具有重要意义,将是今后数学教育领域重要的研究内容之一.
[1] 吴琼,高夯.教师专业知识对高中数学教师各项教学能力影响的调查研究[J].教师教育研究,2015(4):61-71.
[2] Hill H C,Sleep L,Lewis J M,et al.Assessing Teachers’ Mathematical Knowledge:What Knowledge Matters and What Evidence Counts? In:Lester F K.Second Handbook of Research on Mathematics Teaching and Learning[C].Charlotte,NC:Information Age Publishing,2007.
[3] 李士琦.PME:数学教育心理[M].上海:华东师范大学出版社,2000.
[4] 张凯军.师范本科教育与应用型人才培养的教育科学关系[EB/OL].http://www.edu.cn/,2009-01-13.
(责任编辑:张冬冬)
The positive influence of the development of teachers’ subject knowledge on the ‘two levels of thinking’in middle school math’s teaching
PENG Yangui
(School of Mathematics and Information Science,Anshan Normal University,Anshan Liaoning 114007,China)
Learning advanced mathematics has a positive effect on the development of teachers.Although most of the knowledge can not play a role In the teaching process,it is very important in thinking about content of courses,method,structure of course content and so on.Especially,learning the advanced mathematics can train the learner’s thinking to get two levels in the analysis of mathematical content.It is very important in the development of teachers’ subject knowledge.
mathematics teachers in middle school;mathematics courses in universities;the development of teachers’ matter knowledge;the degree of governs
2016-04-18
彭艳贵(1982-),男,辽宁鞍山人,鞍山师范学院数学与信息科学学院讲师.
G6
A
1008-2441(2016)04-0006-04
