Pareto分布的Pearson-χ2距离

季海波

(宿迁学院 文理学院，江苏 宿迁 223800)



Pareto分布的Pearson-χ2距离

季海波

(宿迁学院 文理学院，江苏 宿迁 223800)

对Pareto分布Pa(θ,a)进行研究， 给出两个Pareto分布之间的Pearson-χ2距离的表达式。在两个参数都不同的情况下，得到了两个Pareto分布之间Pearson-χ2的最大距离。此外，在尺度参数a相同情况下，讨论了两个Pareto分布间的最大距离。

密度函数；Pareto分布；距离。

0 引言

在数理统计中，为了比较两个密度函数的差异性，通常利用Pearson-χ2距离来刻画。尽管它们已经不再满足距离公理中的某些条款，但是它们确实能够在某种程度上刻画两个密度函数的差异程度。而且近年来，人们在讨论极值分布的大样本问题、分布函数的计算机模拟样本的收敛性时，Robert等[1]，Liu等[2]和Reiss[3]都使用到了Pearson-χ2距离，作为衡量标准来判断一个密度函数列是否收敛到某个确定的密度函数。因此，可以看出该距离是非常重要的。

Pareto分布是收入分配理论中一种重要的统计分布，最初是由意大利经济学家Pareto作为收入分布在其1895年和1897年的论文中提出的，是一个具有递减的失效函数。Arnold[4]详细论述了Pareto分布的性质及应用，并给出了两参数的分布函数和概率密度函数，分别为：

(1)

其中，θ>0为形状参数，a>0为尺度参数且为门限参数，记Pa(θ,a)。

陈光曙[5]给出了两个分布之间的Pearson-χ2最大距离的相关性质。本文着重讨论两个Pareto分布的Pearson-χ2距离和Pearson-χ2最大距离。

1 伽玛分布的距离

定义1 设随机变量X,Y分别具有密度函数地f(x),g(x)，且f(x)>0，若：

由定义有如下结论成立：

定理1 设f(x),g(x)分别是Pa(θ1,a1)Pa(θ2,a2)的密度函数，则当θ1<2θ2时有，

且1)当θ1→θ2,a1→a2时，d2(f,g)→0；

证明：由于f(x),f(x)分别是Pa(θ1,a1)Pa(θ2,a2)的的密度函数，则：

f(x)=θ1a1θ1x-(θ1+1)(x≥a1;a1,θ1>0)

g(x)=θ2a2θ2x-(θ2+1)(x≥a2;a2,θ2>0)

取a=max{a1,a2}，

(2)

则当θ1<2θ2时有，

(3)

将(3)式带入(2)式有,

(4)

故由定义有，

(5)

显然还有，

1)当θ1→θ2,a1→a2时，d2(f,g)→0；

则定理1得证。

类似地当θ2<2θ1还可以得到

(6)

2 伽玛分布的Pearson-χ2最大距离

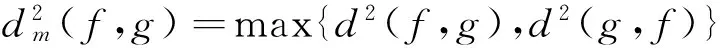
由定义有如下结论成立：

则有，

(7)

且显然有，

则定理得证。

特别地，当a1=a2=a时由如下结论：

且显然有，

[1] Robert G O, Shau S K. Updating schemes, correlation structure, blocking and parameterization for the Gibbssampler[J].J R Statist Soc B,1997,59:291-317.

[2] Liu S J, Wong W H, Kong A. Correlation structure and convergence rate of the Gibbs sampler with various scans[J].J R Statist Soc B, 1995,57:157-169.

[3] Reiss R D. Approximate Distributions of Order Statistics[M].New York: Springer,1980.

[4] Arnold B C. Pareto Distribution[M].Fairland,Maryland：International Co-Operative Publishing House, 1938.

[5] 陈光曙.Pearson-χ2的最大距离的性质[J].辽宁师范大学学报：自然科学版,2005,28(4):402-404.

(责任编辑：孙文彬)

The Study of Pearson-χ2Distance for Gamma Distribution

JI Hai-bo

(School of Liberal and Science, Suqian College, Suqian Jiangsu, 223800, China)

The Pareto distribution Pa(θ,a) is studied, and the expression of Pearson-χ2distance between two Pareto distributions was given. For two different parameters, it sets the Pearson-χ2maximum distance between two Pareto distributions. Moreover, with the same parameter a, it was also discussed..

density function; Pareto distribution;Pearson-χ2distance

2016-08-01

季海波(1981-)，男，江苏南通人，讲师，硕士，主要从事极限理论研究。

O212.62

A

1009-7961(2016)05-0081-04