广义线性模型中变量选择的相合性

张 秋 瑾

(广州航海学院 基础部, 广州 510725)



广义线性模型中变量选择的相合性

张 秋 瑾*

(广州航海学院 基础部, 广州 510725)

在自然联系函数下广义线性模型中,当因变量是一维时,在一定条件下基于Wald检验统计量的变量选择的相合性成立.证明了当因变量为多维时、去掉原有条件中的两个条件,剩下其他条件不变或减弱,该变量选择的相合性仍然成立.该结论推广和改进了原有结果.

广义线性模型; 似然估计; 变量选择; 相合性

1 引言及主要结果

1.1 引言

广义线性模型的理论是对线性模型的经典理论的重要推广, 1972年Nelder 和Wedderburn在文献[1]中引进广义线性模型一词, 自那以后有关研究工作逐渐增加,该模型已应用到许多领域.

考虑一般的广义线性模型

(1)

其中,y1,…,yn是相互独立的q维观察向量, Zi为已知的p×q维设计矩阵,β∈Rp为未知的p维回归参数向量,h是Rq→Rq的一严格单调、充分光滑映射,g=h-1称为联系函数,ei为q维随机误差向量、其均值为零,方差有限.

设q维随机变量yi服从指数型分布,其密度函数为:

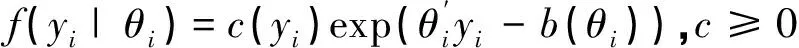
(2)

其中,Θ是自然参数空间,Θ0(Θ的内部组成的集合)非空,b(θ)的各阶导数在Θ0内存在.

易知Θ0为凸区域;yi的均值和方差分别记为μ(θi)、Σ(θi),则有

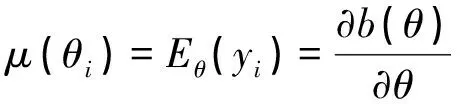
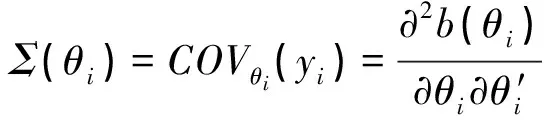
进一步假定Σ(θ)在Θ0是正定的.

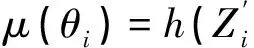
对数似然函数为:

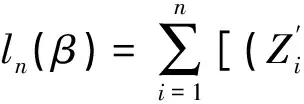
因为c(yi)不依赖于β,对估计β无影响,故相应项可以略去.

似然方程为：

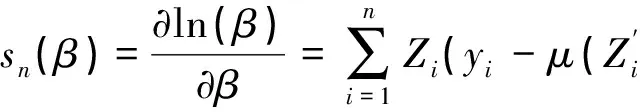
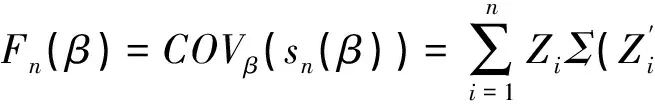
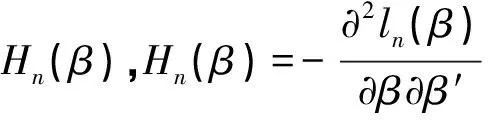
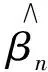
为了后面的叙述先引入以下条件:

(i) B是Rp中开集，序列{Zn}被包含在某一紧集G内,且

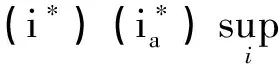
显然条件(i)与条件(i**)等价.

(iii) ∃c0>0,使得Σ(θ)≥c0I，∀θ∈Θ0；

(iii*) ∃c0>0, 使得Σ(θ)≥c0I，∀θ∈Θ.

显然条件(iii)弱于条件(iii*).

定义β0的邻域Nn(δ)(δ>0)如下：

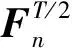
引入以下条件：

(D) λminFn→∞,n→∞；

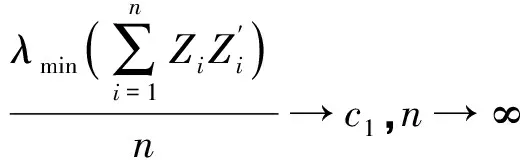
(Sδ) 存在β0的邻域N⊂ B，存在常数δ>0,c2>0,及自然数n1,使得

λminFn(β)≥c2(λmaxFn)1/2+δ，β∈N,n≥n1.

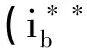
在广义线性模型中最常见的检验问题为:

H0:Cβ0=α,备择假设 H1:Cβ0≠α，

(3)

其中，C是满秩的r×p(r≤p)矩阵.

选取Wald检验统计量

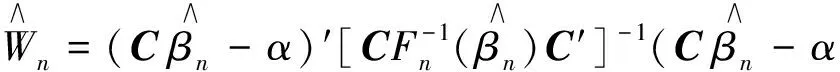
(4)

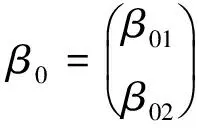
根据文献[3]可知,(3)式可以化简为:

H0:β02=α02,备择假设 H1:β02≠α02.

不失一般性只需考虑

H0:β02=α02,备择假设 H1:β02≠α02.

文献[4]提出了利用Wald检验统计量进行变量选择的方法,具体方法如下:

设D0={k:1≤k≤p,β0(k)≠0}，

(5)

其中,β0(k)表示向量β0的第k个分量.

对D0的估计,称为变量选择问题.考虑以下假设检验:

H0:β0(k)=0，备择假设 H1:β0(k)≠0，

该检验问题可写为:

H0:c′β0=0，备择假设 H1:c′β0≠0，

(6)

其中，c为p维列向量，第k 个元素为1，其余元素为0.设

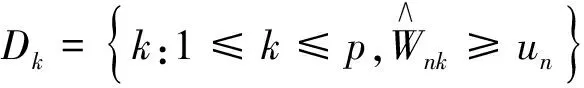
(7)

其中，

(8)

设{un}表示满足下列条件的数列,

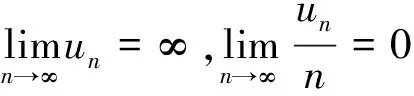
(9)

本文主要的研究工作是在文献[2-3]研究理论基础上,研究了广义线性模型中基于Wald检验统计量的变量选择的相合性问题,证明了因变量y为多维时,若满足条件(i)、(ii)、(iii)、(D*),则Dn是D0的相合估计.由于条件(iii)弱于(iii*),且本文研究条件比文献[4]研究条件要少(N)、(Sδ)这两个条件,而结论却由因变量y一维推广至多维.所以本文基于Wald检验统计量的变量选择的相合性研究结果相比于文献[4]，本文研究条件要弱很多,而结论适用范围却更广.

1.2 主要结论

证明 参见文献[2] 的推论1.

引理2 若条件(i)、(ii)成立,假设检验H0:Cβ0=α，备择假设 H1:Cβ0≠α，

证明 已知条件(i)、(ii)成立,由引理1得 条件(D)、 (N)成立,根据文献[3]定理2得

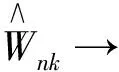
证明 检验问题H0:β0(k)=0

可写为

H0:c′β0=0,备择假设 H1:c′β0≠0.

根据引理2可得

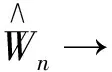
根据(4)知C=c′,α=0代入(4)式得

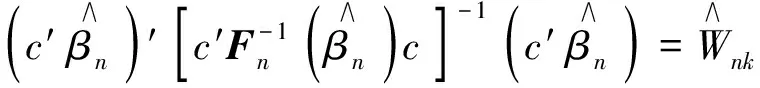
故

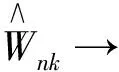
定理1 若条件(i)、(ii)、(iii)、(D*)成立,{un}是满足(9)式的数列,则由(7)式定义的Dn是由(5)式定义的D0的相合估计.

2 定理1的证明

证明 1) 当β0(k)=0时,即kD0时，根据引理3,得当β0(k)=0时,

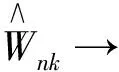
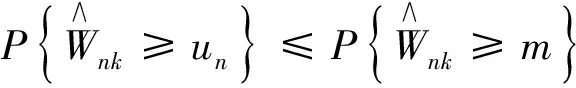
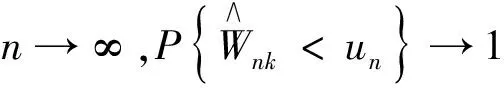
2) 当β0(k)≠0时,即k∈D0时，考虑统计量

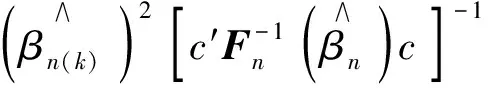
根据条件(iii)有

∃c0>0, 使得Σ(θ)≥c0I,∀θ∈Θ0.

(10)

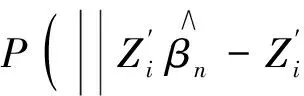
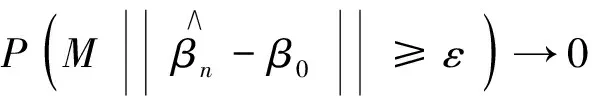
从而有

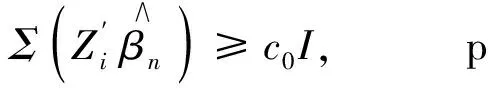
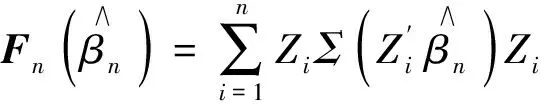
根据(10)式有

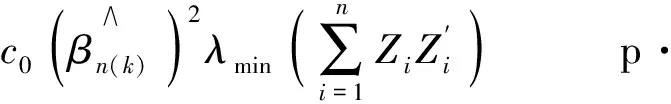
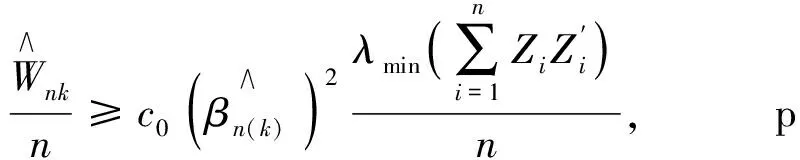
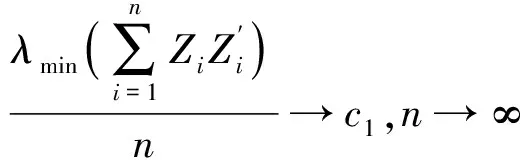
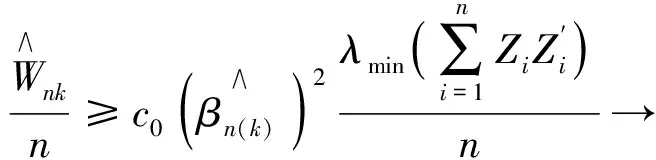
c0c1(β0(k))2>0, p·.

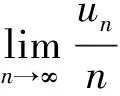
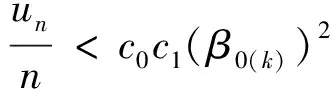
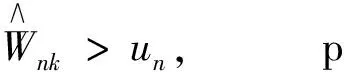
由1)、2)可得Dn是D0的相合估计.

[1] NELDER J A, WEDDERBURNR R W M. Generalized linear models[J].Journal of Roy Statististical Society Series A(General), 1972, 135(3):370-384.

[2] FAHRMEIR L,KAUFMANN H.Consistency and asymptotic normality of the maximum likelihood estimator in generalized linear models[J].The Annals of Statistics, 1985, 13(1):342-368.

[3] FAHRMER L. Asymptotic testing theory for generalized linear models[J]. Statistics, 1987, 18(1):65-76.

[4] 蔡 鹏, 高启兵. 广义线性模型中的变量选择[J].中国科学技术大学学报, 2006, 36(9):927-931.

The consistency of variable selection for generalized linear models

ZHANG Qiujin

(Division of Basic Science， Guangzhou Maritime College， Guangzhou 510725)

In generalized linear models under natural link function， when the dependent variable is one-dimensional， the variable selection is consistent under indicated conditions upon the Wald test statistics. In the present study， it is demonstrated that the consistency of variable selection remains when applied in multi-dimensional situation with two original conditions removed and others unchanged or weakened. This result expands and improves the original one．

generalized linear models； maximum likelihood estimator； consistency; variable selection

2015-05-15.

广东省教学科学十二五规划课题项目(2011TJK182);广州航海学院自然科学基金项目(201212B08).

1000-1190(2016)01-0028-04

O212

A

*E-mail: zhangqiujin@126.com.