中长期电量预测的傅里叶马尔科夫修正模型

李欣然+陈鸿琳+冷华+陈国民

摘 要：灰色模型在中长期电量预测中只对电量呈近似指数规律单调增长的序列才有较高的预测精度.随着电量变化随机波动性的增强，建立新的修正预测模型是十分必要的.针对灰色模型抗干扰能力差的问题，提出了灰色预测的傅里叶马尔科夫修正模型，先利用傅里叶级数法，提取周期信息，优化电量变化的指数率，再采用马尔科夫链法，将电量波动随机性嵌入模型之中，从而对灰色预测的原始残差进行二重修正，提高预测模型的适应性和灵活性.通过实例分析以及对比验证表明，该模型有效地提高了预测精度.

关键词：电量预测； 灰色模型； 残差修正； 傅里叶级数； 马尔科夫链

中图分类号 TM715 文献标识码 A

文章编号：1674-2974（2016）10-0062-08

Abstract：Gray model is widely used in mid-long term electricity demand forecasting， but the model fits exponentially increasing data more precisely. Due to China's economic growth rate fluctuations， the increase in electricity consumption is slowing down， and electricity varies stochastically. So it is necessary to propose a new model to reflect the new situation. To solve the problem of the poor anti-interference ability of grey model， this paper proposes a model with Fourier series and Markov theory residual error correction based on grey model. This model applies Fourier series method to optimize electricity changing rate， and Markov chain method to embed the random property in gray forecasting model for doubly correcting the residual error， which can improve the adaptability and flexibility. The proposed model is verified by actual load data， and it indeed improves the forecasting accuracy.

Key words：load forecasting； grey model； residual error correction； Froier series； Markov chain theory

中长期电量预测多指年度预测和月度预测，对电力部门的发展规划有重要意义，电量预测有利于提高电网运行的安全性和经济性.当经济增长，用电需求呈逐年递增的趋势时，灰色预测模型[1]能较好地以指数形式拟合中长期用电量情况.但是用电量还受到政治、经济事件以及气候因素的影响，具有一定的随机性与波动性，电量并不是按照绝对的指数规律逐年递增，近年来却出现了增速放缓的现象，有的地区甚至出现负增长，此时若不对灰色模型预测结果进行修正，会产生较大的误差.

实际上，对时间序列残差的修正由来已久亦非常普遍[2-3]，电力系统应用中多先对残差绝对值进行灰色预测，继而采用马尔科夫状态转移来判断残差的正负符号，以修正原预测模型[4].而残差序列一般波动剧烈，没有明显的规律，用含有明显指数规律的灰色模型对其进行拟合和预测都将存在较大的误差.此外，在将马尔科夫理论用于电力系统时，有学者运用马尔科夫状态转移概率矩阵直接修正残差值[5]，有一定改善.

本文利用傅里叶级数法对时间序列残差的良好修正效果[6-7]，将其运用到灰色预测模型，作为一次修正，周期信号或者任何满足条件可延拓的信号都可以展开成傅里叶级数，从而可以提炼出数据样本序列中隐含的周期信息，改善灰色模型自身的机理缺点，使预测结果不再呈现单一的指数增长，以适应不同变化规律的电量序列；同时对原始残差进行马尔科夫预测，作为二次修正，马尔科夫预测能够反映状态的随机过程，提高其随机灵动性.因而本文提出了一种傅里叶马尔科夫残差修正的中长期电量灰色预测模型（GM-FM，Grey Model-Fourier Markov Residual Correction）.在此基础上，以实际用电量数据做算例分析，并与现有修正方法进行对比，结果表明，本文所提模型较大程度地提高了预测精度.

1 灰色GM（1，1）模型

灰色系统理论主要通过对部分已知信息的生成、开发，提取有价值的信息，实现对系统运行行为、演化规律的正确描述和有效监控，灰色预测是一种对含有不确定因素的系统进行预测的方法.

通过对原始数据序列进行累加生成可以弱化随机性，得到指数规律性较强的曲线.而电力系统的发展与社会、经济系统一样受到各种因素的制约，不可能永远按照某一速度发展，有时发展较快，有时发展较慢[9].从而GM（1，1）模型的应用有很大的局限性，只有当系统基本按指数规律发展，且发展速度不是很快时，才能得到精准的预测结果.为了改进GM（1，1）建模机理本身的缺陷，通过修正残差，即实际值与预测值之差，来提高预测精度.

2 傅里叶残差修正

如前所述，电量受众多因素影响，不同时期会以不同的指数率变化.傅里叶级数是周期函数，可提炼出数据样本序列中隐含的周期信息，起到降噪作用[6-7，10-11].事实上，任何周期函数或满足条件的可延拓的非周期函数都可以展开成为傅里叶级数，并且可用正弦函数和余弦函数构成的无穷级数来表示，成为一种特殊的三角级数.而三角函数又根据欧拉公式可化为指数形式，故傅里叶级数也可称为一种指数级数，这恰好能与GM（1，1）模型相结合，提炼数据序列不同的指数信息，并改善GM（1，1）模型中累加生成单一指数变化率的局限性.傅里叶残差修正的具体步骤如下：

傅里叶级数对灰色模型的残差修正还可以应用于灰色Verhulst模型[14]等改进灰色模型中，同样取得了较好的改进精度.但是电量的变化不仅仅只有呈近似指数规律增长的特点，还有很强的随机性，受到各类事件的影响.因此，在傅里叶修正残差改善预测模型的基础上，本文进一步通过马尔科夫链来预测残差，进行二重修正，以提高预测精度.

3 马尔科夫残差预测

马尔科夫链是指对于任一随机过程，某一时刻之后的状态只与该时刻有关，与该时刻之前的状态无直接关系[15].该方法促进了随机过程理论的发展，即Markov过程，成为了概率论的新分支.用电量变化受到诸多因素的影响，其增长速率及是否增长都是不能完全确定的，表现出马尔可夫残差预测的性质，具备较强的随机性，采用马尔科夫残差预测可以改善序列的随机特征，优化预测结果.设随机系统Y在时刻t处于状态in，则在t+1时刻系统所处的状态与t时刻之前的状态无关，换而言之初始时刻到t-1时刻的随机过程均不影响t+1时刻，即：

本文改进后GM-FM模型与GM模型的预测精度对比分析如表5所示，曲线及其放大图如图1所示.可见本文所提方法的拟合精度和预测精度均明显提高，证明了GM-FM模型的有效性.

此外，对文献[5]中1979-1989年石家庄售电量数据对1989年的售电量进行了预测验证，并与之所提的马尔科夫预测残差及其残差符号的方法做了对比，同样证明本文所提模型具有更高的预测精度.本文所提方法具体数据如表6所示，曲线及其放大图如图2所示，其中由3步转移矩阵得到的Markov残差预测值为0.021 6，与该文献的预测结果对比如表7所示.

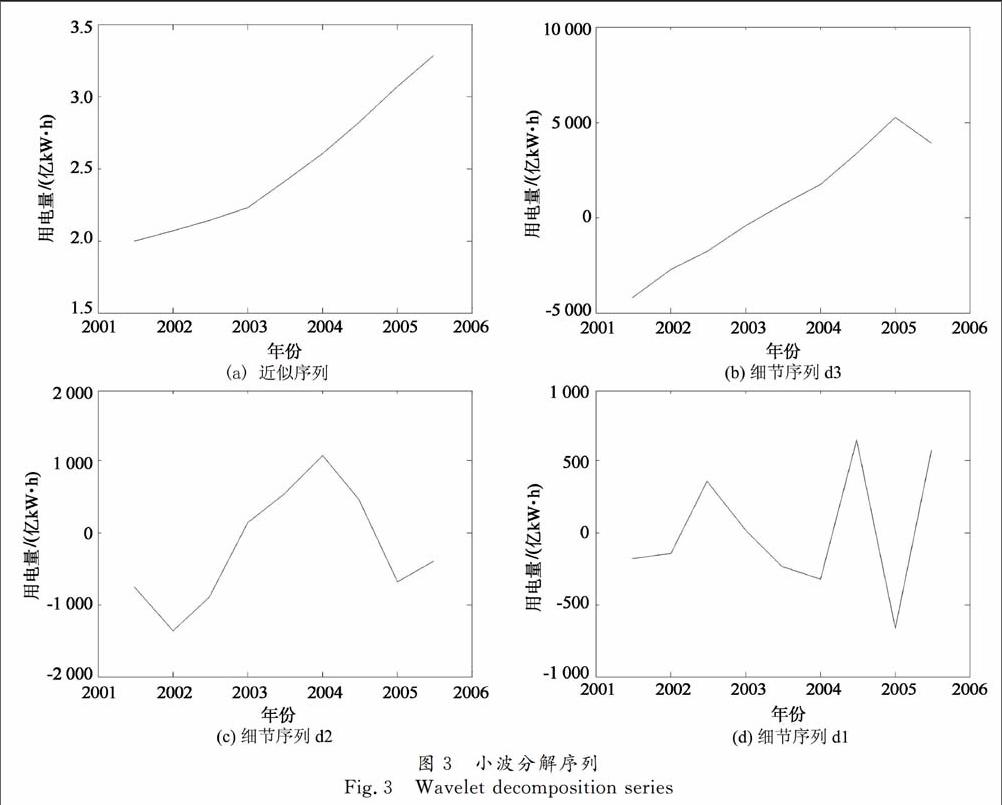
另外，对比同样由傅里叶分析思想发展而来的小波分析方法，其通常需要先对原始序列进行小波分解，再根据分解后的信号特征选用合适的方法进行组合预测，最后重构（叠加）近似序列和细节序列的预测结果得到总的预测值.将本文中已有的2000-2009年的用电量作为原始序列进行小波分解，小波函数采用Daubechies系列的db3小波，作3层分解，结果如图3所示，分别为近似序列（趋势项）a3和细节序列（高频分量）d3，d2和d1.

由图可见，分解后的近似序列有更平稳的指数增长规律，但其细节序列都波动复杂，非线性极强，选用哪种或哪几种合适的预测方法是工作的一大难点，模型变得复杂，且解构、重构后的预测结果难免存在机理上的误差.更加值得一提的是，选用何种小波函数进行何种尺度的分解需要依靠经验和试验，选择不当可能带来很大的误差.相比之下，本文所提方法不需要采用多种不同模型的组合预测，提取序列自身的信号特征，进行预测和修正，更为简单，且效果良好.

5 结 论

灰色模型能较好地预测中长期电量，但电量数据增长速度有时快有时慢，更有诸多因素的随机影响，单纯的灰色模型对数据波动且不按单一指数规律变化的序列适应性不强.本文通过分析电量预测的残差数列，利用傅里叶级数和马尔科夫状态转移矩阵对预测结果进行了二重修正，改善了灰色模型对样本数据波动适应能力不足的缺点，使其具备更为灵活的指数率以及随机适应性等特点，显著提高了预测精度，通过对2010年中国全社会的用电量以及石家庄1989年的售电量数据进行预测分析，验证了该模型的准确性，且通过对比可知，模型预测结果优于现有的一般单纯使用马尔科夫修正残差的方法.

参考文献

[1] 邓聚龙. 灰色系统理论[M].武汉：华中理工大学出版社，1990.

DENG Ju-long. Grey system theorg[M].Wuhan：Huazhong University of Science Technology Press，1990.（In Chinese）

[2] BOX G P， JENKINS G M.Time series analysis： forecasting and control[M].San Francisco，CA：Holden-Day InC.1976.

[3] 任震， 吴敏栋， 黄雯莹. 电力系统可靠性原始参数的滚动预测和残差修正[J]. 电力自动化设备， 2006，26（7）：10-12.

REN Zhen， WU Min-dong， HUANG Wen-ying. Rolling prediction and residual error revise of original reliability parameter of power system[J]. Electric Power Automation Equipment， 2006，26（7）：10-12. （In Chinese）

[4] 王翠茹， 孙辰军， 杨静，等. 改进残差灰色预测模型在负荷预测中的应用[J]. 电力系统及其自动化学报， 2006，18（1）：86-89.

WANG Cui-ru， SUN Chen-jun， YANG Jing， et al. Application of modified residual error gray prediction model in power load forecasting[J]. Proceedings of the CSU-EPSA， 2006， 18（1）： 86-89. （In Chinese）

[5] 黄银华， 彭建春， 李常春，等. 马尔科夫理论在中长期负荷预测中的应用[J]. 电力系统及其自动化学报，2011，23（5）：131-136.

HUANG Yin-hua， PENG Jian-chun， LI Chang-chun， et al. Application of markov theory in mid-long term load forecasting[J]. Proceedings of the CSU-EPSA， 2011， 23（5）： 131-136. （In Chinese）

[6] 黄元生， 方伟. 基于灰色傅里叶变换残差修正的电力负荷预测模型[J]. 电力自动化设备， 2013，33（9）：105-112.

HUANG Yuan-sheng， FANG Wei. Power load forecasting model with residual error correction based on gray Fourier transform[J]. Electric Power Automation Equipment， 2013，33（9）：105-112. （In Chinese）

[7] TAN C L， CHANG S . Residual correction method of fourier series to GM（1，1） model[C].Proceedings of the National Conforence of Grey Theory and Application，Kaohsiung， Taiwan：1996：93-101.

[8] 刘洋， 陈传波， 王国霞. 基于灰色系统理论的湖南省电力需求分析与预测[J]. 湖南大学学报：自然科学版， 2005， 32（5）： 71-74.

LIU Yang， CHEN Chuan-bo， WANG Guo-xia， et al. Power system stabilizer based on grey prediction and extension control[J]. Journal of Hunan University：Natural Sciences， 2005，32（5）： 71-74. （In Chinese）

[9] 陈章潮， 熊岗. 应用改进的灰色GM（1，1）模型进行长期电力需求预测[J]. 电力系统自动化， 1993，17（7）：20-24.

CHEN Zhang-chao， XIONG Gang. Long-term load forecasting for pudong new area of shanghai using grey theory[J]. Automation of Electric Power Systems， 1993， 17（7）： 20-24. （In Chinese）

[10]甘丽珍， 张铭鑫， 刘明周，等. 基于傅里叶变换的质量预测动态残差修正模型[J]. 合肥工业大学学报：自然科学版， 2009，32（6）：806-810.

GAN Li-zhen， ZHANG Ming-xin， LIU Ming-zhou， et al. Research on the dynamic model of error amendment for quality prediction based on Fourier transform[J]. Journal of Hefei University of Technology ：Natural Sciences， 2009， 32（6）： 806-810. （In Chinese）

[11]柳焕章， 贾晓辉. 自适应突变量继电器及其傅里叶算法[J]. 电力系统自动化， 2011，35（20）：74-77.

LIU Huan-zhang， JIA Xiao-hui. Adaptive variation relay and its fourier agorithm[J]. Automation of Electric Power Systems， 2011， 35（20）： 74-77. （In Chinese）

[12]曹健， 林涛， 徐遐龄，等. 基于最小二乘法和时频原子变换的谐波/间谐波测量算法[J]. 电工技术学报， 2011，26（10）：1-7.

CAO Jian， LIN Tao， XU Xia-ling， et al. Monitoring of power system harmonic/inter-harmonics based on least squares algorithm and time frequency transform[J]. Transactions of China Electrotechnical Society， 2011， 26（10）： 1-7. （In Chinese）

[13]SU Shun-feng ， LIN Chan-ben，HSU Yen-tseng. A high precision global prediction approach based on local prediction approaches[J]. IEEE Transactions on Systems， man， and Cybernetic-part C： Applications and Reviews，2002，32（4）：416-425.

[14]KAVACAN E， ULUTASl B， KAVNAK O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications， 2010，37（2）：1784-1789.

[15]鲁文军， 陈远扬， 刘觉民，等. 电力设备可靠性评估的RSS方法研究[J]. 湖南大学学报：自然科学版， 2011，38（4）：47-50.

LU Wen-jun， CHEN Yuan-yang， LIU Jue-min， et al. Research of RSS in power equipment reliability evaluation[J]. Journal of Hunan University：Natural Sciences， 2011，38（4）：47-50. （In Chinese）

[16]郑雅楠， 单葆国， 顾宇桂，等. 中长期电量灰色预测中数据预处理方法研究[J]. 中国电力， 2013，46（10）：111-114.

ZHENG Ya-nan， SHAN Bao-guo， GU Yu-gui， et al. Data preprocessing for grey model of medium-long term load forecasting[J]. Electric Power， 2013， 46（10）： 111-114. （In Chinese）