对偶体积差Lp-Brunn-Minkowski不等式

何 娟

(重庆师范大学 数学科学学院，重庆 401331)



对偶体积差Lp-Brunn-Minkowski不等式

何 娟

(重庆师范大学 数学科学学院，重庆 401331)

介绍了对偶体积差和均质积分差的概念，讨论了它们的对偶Lp-Brunn-Minkowski型理论，其中一个结论表明，对于两个相互扩张的星体，特别地，当它们中挖掉两个任意的星体后，Lp-Brunn-Minkowski不等式仍然成立.

星体；凸体；对偶体积差；对偶Lp-Brunn-Minkowski不等式；对偶均质积分差

设K,L是Rn里的凸体(有非空内点的紧凸集).设V表示体积，+p表示p-和.经典的Lp-Brunn-Minkowski不等式[1]表示如下:

等号成立当且仅当K和L互为伸缩的.

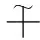
等号成立当且仅当K和L互为伸缩的.

在2010年，吕松军建立了对偶体积差的Brunn-Minkowski不等式和Minkowski不等式[2].

定理1 假设K，L和D是Rn里的星体，并且D⊇K，D′⊇L，D′是D的一个扩张，则:

等号成立当且仅当K和L是相互扩张的并且(V(K),V(D))=c(V(L),V(D′))，其中c是一个常数.

其中ρK(θ)是K的径向函数，定义为ρK(θ)=max{λ≥0:λθ∈K},θ∈Sn-1.并且dθ是B的表面积元素，Rn里的标准单位球.

定理2 假设K，L和D是Rn里的星体，并且D⊇K，D′⊇L，D′是D的一个扩张,则:

等号成立的条件当且仅当K和L是相互扩张的并且(V(K),V(D))=c(V(L),V(D′))，其中c是一个常数.

文献[2]的第一个结果(定理1)表明了两个相互伸缩的星体，其中挖去两个任意的星体，对偶体积差Brunn-Minkowski不等式成立.本文将用分析的方法来建立对偶体积差的Lp-Brunn-Minkowski不等式，下面是主要结果.

定理3 假设M，K和L是Rn里的星体，并且K⊆M，L⊆M′，M′是M的一个扩张，则:

等号成立当且仅当K和L是相互扩张的并且(V(M),V(K))=c(V(M′),V(L))，其中c是一个常数.

其中ρk(θ)是K的径向函数，定义为ρk(θ)=max{λ≥0:λθ∈K}，θ∈Sn-1.

两个星体的对偶体积差Lp-Minkowski不等式能表示为定理4[4]：

定理4 假设M，K和L是Rn里的星体，并且K⊆M，L⊆M′，M′是M的一个扩张，则:

等号成立当且仅当K和L是相互扩张的并且(V(M),V(K))=c(V(M′),V(L))，其中c是一个常数.

本文另一个目标是介绍凸体的均质积分差，进而了解它的对偶Lp-Brunn-Minkowski不等式.

1 预备知识

首先引入一些关于星体的对偶Lp体积、星体的对偶均质积分差以及星体的对偶体积差的一些基本结论.对偶体积差[2]以及对偶均质积分差的概念也会给出.关于Brunn-Minkowski理论和它的对偶可以参看文献[3-8].

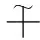
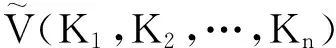
(1)

两个紧域的体积差概念参看文献[9].

(2)

2 对偶体积差不等式

本节将建立关于星体的两个对偶体积差不等式，这也是定理3的推广.关于对偶的一些体积差不等式可以参看文献[10].

定理5 设K，L和M是Rn里的星体，M′是M的一个伸缩，如果p≥1，K⊆M,L⊆M′，则:

(3)

推论1 假设R(K),R(L)是星体K,L的内径，使得R(K)≤r1,R(L)≤r2,p≥1，则有:

等号成立当且仅当K,L是互为伸缩的且r1/r2=V(K)/V(L).

本文将需要一些额外的定义来分析定理5的不等式，首先定义一个函数Φp(x)为:

引理1 如果p>1，x,y∈Rp，则x+y∈Rp，有:

(4)

如果p<0或0

(5)

式(4)和式(5)等号成立当且仅当系数x,y成比例.

引理1的证明可以参看文献[11].不等式(5)首先是Bellman证明的，熟知的Bellman不等式.

定理1的证明： 关于体积的对偶Lp-Brunn-Minkowski不等式如下：

(6)

(7)

根据式(6)、(7)和Bellman不等式(4)，有：

3 对偶Lp-均质积分差不等式

本节将建立两个关于星体的Lp-均质积分差不等式.

定理6 设K，L和M是Rn里的星体，M′是M的一个伸缩.

如果p≥1，0≤i≤n-1，K⊆M,L⊆M′，则：

(8)

如果K⊆M,L⊆M′，n-1n，p>1，则：

(9)

证明 设0≤i≤n-1，i∈R，对偶Lp-均质积分的对偶Lp-Brunn-Minkowski不等式如下：

(10)

(11)

从式(10)、(11)以及Bellman不等式，得到：

[1]GARDNERRJ.Geometric[MJ].NewYork:CambrigeUniversityPress，1995.

[2] LV S J.Dual Brunn-Minkowski inequality for volume differences[J].Geom Dedicata,2010,145:169-180.[3]GARDNERRJ.TheBrunn-Minkowskiinequality[J].BullAmerMathSoc,2002,39:355-405.

[4] SCHNEIDER R.Convex Bodies: The Brunn-Minkowski Theory[M].New York:Cambrige University Press,1993.

[5] LUTWAK E.Dual mixed volumes[J].Pacific J Math,1975,58:131-159.

[6] LENG G S.The Brunn-Minkowski inequality for volume differences[J].Adv Appl Math,2004,32:615-624.

[7] LOSONCZI L,PLES Z S.Inequalities for forms[J].J Math Anal Appl,1997,205:148-156.

[8] LUTWAK E,YANG D,ZHANG G Y.The Brunn-Minkowski-Firey inequality for nonconvex sets[J].Adv Appl Math,2012,48:407-413.

[9] LUTWAK E.Intersection bodies and dual mixed volumes[J].Adv Math,1988,71:232-261.

[10] FENG Y,WANG W,YUAN J.Differences of quermassintegral and dual quermassintegrals Blaschke-Minkowski and Radial Blaschke-Minkowski Homonorphisms[J].Bull Belgian Math Soc,2014,21:577-592.

[11] LUTWAK E.The Brunn-Minkowski inequality for volume differences[J].Adv Appl Math,2004,32:615-624.

责任编辑：时 凌

Dual Lp-Brunn-Minkowski Inequality for Volume Differences

HE Juan

(School of Mathematics,Chongqing Normal University,Chongqing 401331,China)

In this paper,we introduce the concepts of the dual volume differences and width-integral differences,and discuss the theory of dual Lp-Brunn-Minkowski type for them.One of the results implies that for two mutually dilating star bodies,the dual Lp-Brunn-Minkowski inequality still holds after two arbitrary star bodies included in them are excluded.

star body;convex body;dual volume difference; dual Lp-Brunn-Minkowski inequality;dual quermassintegral differences

2016-06-09.

国家自然科学基金面上项目(11271390).

何娟(1990- )，女，硕士生，主要从事凸几何的研究.

1008-8423(2016)03-0285-03

10.13501/j.cnki.42-1569/n.2016.09.010

O18

A