基于EC细网格产品对怀化地区日最高气温的预报及订正分析

王 强，张 骁，王起唤

(湖南省怀化市气象台，湖南 怀化 418000)



基于EC细网格产品对怀化地区日最高气温的预报及订正分析

王 强，张 骁，王起唤

(湖南省怀化市气象台，湖南 怀化 418000)

利用EC细网格(ECMWF-thin)0.125°×0.125°格距20时起报地面2 m气温资料，使用反距离加权法插值至怀化11个国家气象观测站点上，计算出模式预报的日最高气温，对模式预报准确率的时空分布特征以及利用N日误差滑动平均值、天气分类方法分别对模式预报进行订正分析发现：随着预报时效的延长ECMWF-thin日最高气温预报准确率降低，存在明显的时间变化特征，但空间差异不明显；ECMWF-thin日最高气温预报较实况普遍偏低；利用N日误差滑动平均值方法订正，日最高气温预报准确率的提升16%～20%，订正后预报准确率在54%～73%，此方法操作便捷、简单实用；进行天气分类订正后，各类型天气均有不同程度提升，且对特定类型天气提升明显，两种方法各有利弊，对日最高气温预报均具有一定的指导意义。

气温，订正，滑动平均，天气类型

1 引言

怀化地处湖南西南部，地型呈西南—东北向狭长带状，南北长353 km，东西宽229 km，总面积2.76万km2。全境地势起伏，沟壑纵横，东南部有雪峰山，西北部有武陵山，海拔在300 m以上的山地占总面积的73%，特殊的地形分布，海拔高度差异显著，也导致怀化各地气温分布特征各异，加之日最高气温对天空状况的敏感性强，模式预报在日最高气温要素的预报上往往达不到直接使用的要求，而在实际预报中，对于差异显著的气温要素预报，随着预报时效延长，预报员对气温要素的能力显著减弱。为掌握气温分布规律，探索有效的气温预报方法，国内学者做了许多研究，周青[1]等、李军[2]等、汪卫平[3]等利用标准化均方根误差分析、气温空间分布的地形调节统计模型等方法分析地面气温分布特征；周婷婷[4]等、李莎[5]等、邱学兴[6]等、刘宇[7]等、周继先[8]等、陈晓燕[9]等利用 MODIS影像数据和数字高程模型差值、Kriging插值、Barnes 插值和一阶卡尔曼滤波订正方法、空间卷积算法最小二乘法、支持向量积法等方法探索适合中国区域的地面气温插值方法；薛志磊[10]等、张杰[11]等也将数值预报的动力释用方法、多模式集合等应用到气温预报中。社会公众对气象预报关注度越来越高，最高气温预报是公众气象预报的一项重要内容，同时作为城镇预报的考核之一。数值预报产品，尤其是气温预报产品已成为预报员在日常气象预报的主要参考依据，但是由于模式预报中对气温的预报资料局限性以及模式自身预报偏差，导致模式预报很难直接应用到城镇预报中去，本文试图从ECMWF-thin日最高气温预报误差出发，寻找适合本地订正方法，指导日最高气温预报。

2 资料方法

2015年1月15日之后，ECMWF-thin对地面2 m气温的要素预报由0.25°×0.25°的格点预报场调整为0.125°×125°的格点预报，预报时间间隔仍然是0～72 h为每3 h一次，72 h之后每6 h一次，为保证资料一致性，本文选取研究时段为2015年2月1日—2016年1月31日，共计365 d。

2.1 资料选取

选取欧洲中心每天20时起报，对未来120 h时效的高温预报资料，利用反距离加权法将每个预报时次温度预报插值到怀化市11个县预报站点上，以20时为日界，计算出逐24 h气温最高值作为日最高气温预报值；选取怀化市11个国家气象站逐分钟气温资料，以20时为日界，获取每天最高气温值为日最高气温实况；从国家卫星气象中心的风云卫星遥感数据服务网下载FY-2F总云量(CTA)逐小时数据，根据日最高气温出现的时段，选取每日的10时、12时、13时、14时、15时、16时、17时的总云量来计算平均总云量，结合每日的降水情况，将天空类型分为以下3个大类型6个小类型。

表1 天气类型分型

2.2 资料处理方法

根据《全国城镇天气预报质量检验方案》、《湖南省城镇天气预报质量检验方法》、《中短期天气预报质量检验办法(试行)》中日最高气温检验标准，首先利用实况资料对ECMWF-thin的日最高气温资料进行检验，总结模式日最高气温预报的时空分布特征。温度预报具体检验标准为：

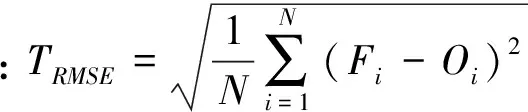
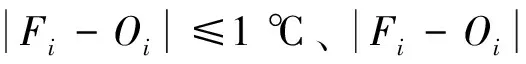
温度预报准确率的实际含义是温度预报误差≤2 ℃的百分率。

根据ECMWF-thin日最高气温预报与日最高气温实况误差，以前N日预报与实况误差的滑动平均值作为订正值，对未来最高气温预报进行订正并检验。

其中，前N日预报与实况误差滑动平均值=(预报前1天的误差值 +预报前2天的误差值+…+预报前N天的误差值)/N。

结合天气类型的分型和ECMWF-thin最高气温预报偏差分析，对不同天气类型下模式最高气温预报分别进行订正并检验，具体天气类型分型如表1。

3 ECMWF-thin最高气温预报分析

3.1 模式预报准确率检验分析

3.1.1 时间变化特征 从ECMWF-thin不同预报时效全市各站日最高气温月平均预报准确率图(图1)中可以看出：

图1 ECMWF-thin不同预报时效全市各站日最高气温月平均预报准确率图Fig.1 ECMWF-thin monthly mean forecast accuracy diagram of all stations' daily maximum temperature in different forecast time limits

①模式预报准确率随着预报时效的延长，呈下降趋势，在2—4月尤为明显；最高值出现在12月份24 h时效，为78.30%；最低值出现在4月份120 h时效，为15.99%。

② 0～120 h各预报时效逐月平均预报准确率在15%～79%之间，各月之间差异很大， 1—4月呈下降趋势，4月达到全年最低值，出现第1个波谷，各时效均值为25.27%； 5月开始上升，5—8月又呈下降趋势，8月迎来第2个波谷，各时效均值为26.42%；9月有所升高，10月又出现波动性下降，各时效准确率均值为35.49%；之后准确率呈现逐步上升趋势。

3.1.2 空间变化特征 ECMWF-thin对怀化11县逐24 h预报时效日高温预报准确率均是随着预报时效的延长而减小，在0～24 h时效内，麻阳县最低为47.34%，辰溪最高为59.66%，平均53.55%；24～48 h时效内，新晃县最低为36.93%，辰溪县最高为53.69%，平均47.62%；48～72 h时效内，新晃县最低为38.31%，沅陵县最高为51.55%，平均45.97%；72～96 h时效内，新晃县最低为35.71%，沅陵县、洪江市最高为41.43%，平均40.05%；96～120 h时效内，怀化站最低为36.08%，辰溪最高为43.18%，平均39.93%，从图中可以看出在各时效内，ECMWF-thin对各县日最高气温预报准确率有所差异，但相差较小。

图2 ECMWF-thin对怀化市11县日最高气温各预报时效预报准确率(a)ECMWF-thin(b：24 h，c:48 h，d:72 h，e:96 h，f:120 h)时效11县日最高气温预报准确率时序变化图Fig.2 ECMWF-thin forecast accuracy diagram of 11 counties' daily maximum temperature in different forecast time limits (a); ECMWF-thin forecast accuracy time series diagrams of 11 counties' daily maximum temperature in the time limits of b:24 h, c:48 h, d:72 h, e:96 h, f:120 h

分析0～24 h、24～48 h、48～72 h、72～96 h、96～120 h时效内怀化市各县日最高气温预报准确率时序变化(图2b～2f)，各时效范围内与怀化全市对应时效内的预报准确率(图1)具有相似的变化趋势，且相同时效范围，模式对怀化各县日最高气温预报准确率具有相似变化趋势。

3.2 ECMWF-thin日最高气温预报误差分析及成因探讨

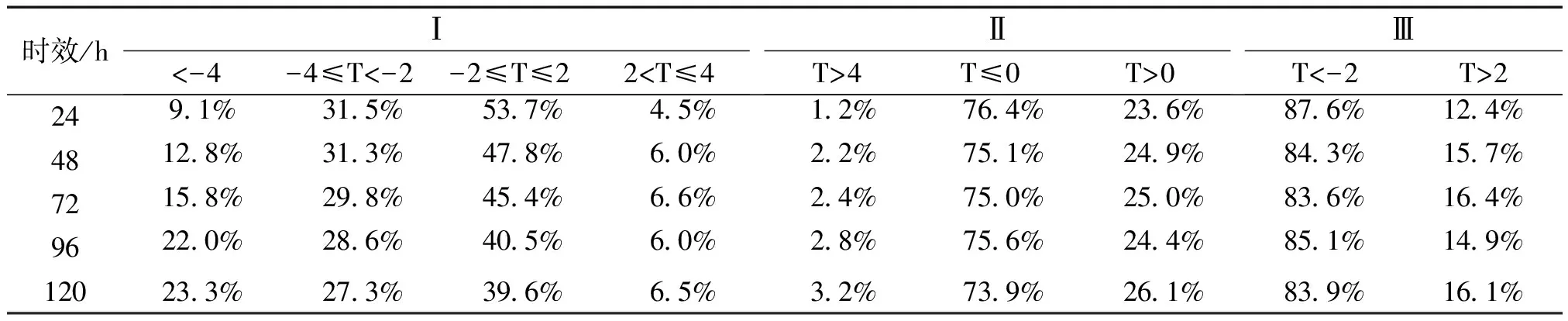
表2 出现各预报偏差概率(T=ECMWF-thin日最高气温预报值-对应时段日最高气温实况)

注：Ⅰ、Ⅱ统计内容为各预报偏差段占全年所有站次比重，Ⅲ统计内容为指定预报偏差占绝对误差>2 ℃(判定为预报错误)中比重。

从表2中可以出，ECMWF-thin的日最高气温预报73%以上的预报都较实况偏低；日最高气温绝对误差在2 ℃以上的(按照评分标准判断为预报错误)，其中模式偏低情况，各预报时效均在83%以上，0～24 h更是达到了87.6%。

成因探讨：

①怀化市属中亚热带季风气候区，四季分明，不同季节气温差异较大，变化幅度也不尽相同，由于气温升降明显，变化幅度大，加大了日最高气温的预报难度。从图3中可以看出怀化市高低温温差与模式对日最高气温预报准确率呈明显负相关关系。

图3 怀化市日高低温实况温差和ECMWF-thin日最高气温预报准确率时序变化图Fig.3 Difference between actual daily maximum and minimum temperature in Huaihua and ECMWF-thin forecast accuracy time series diagram of daily maximum temperature

②ECMWF-thin对地面2 m气温要素预报格式和日最高气温出现时间导致了预报偏差的存在，进而影响预报准确率。ECMWF-thin对地面2 m气温要素预报在前72 h时效是对逐3 h整点气温也就是每天的02时、05时、08时、11时、14时、17时、20时、23时的8个时次的整点气温进行预报，72 h～120 h时效范围内是对逐6 h也就是02时、08时、14时、20时的4个时次的整点预报进行预报，在实际预报中，我们是根据具体的预报日界，将预报范围内的所有整点数据的最大值作为日最高气温的预报值，从对怀化全市2015年日最高气温在全天各时段出现频率的统计来看(图4)，极少数日最高气温出现在整点，日最高气温主要出现在11—18时之间，占90.77%，12—17时占80.78%，而在14—17时之间ECMF-thin没有气温预报数据，这个时段的高温出现概率则高达63.40%，这也直接影响了ECMWF-thin日最高气温预报的预报准确率。

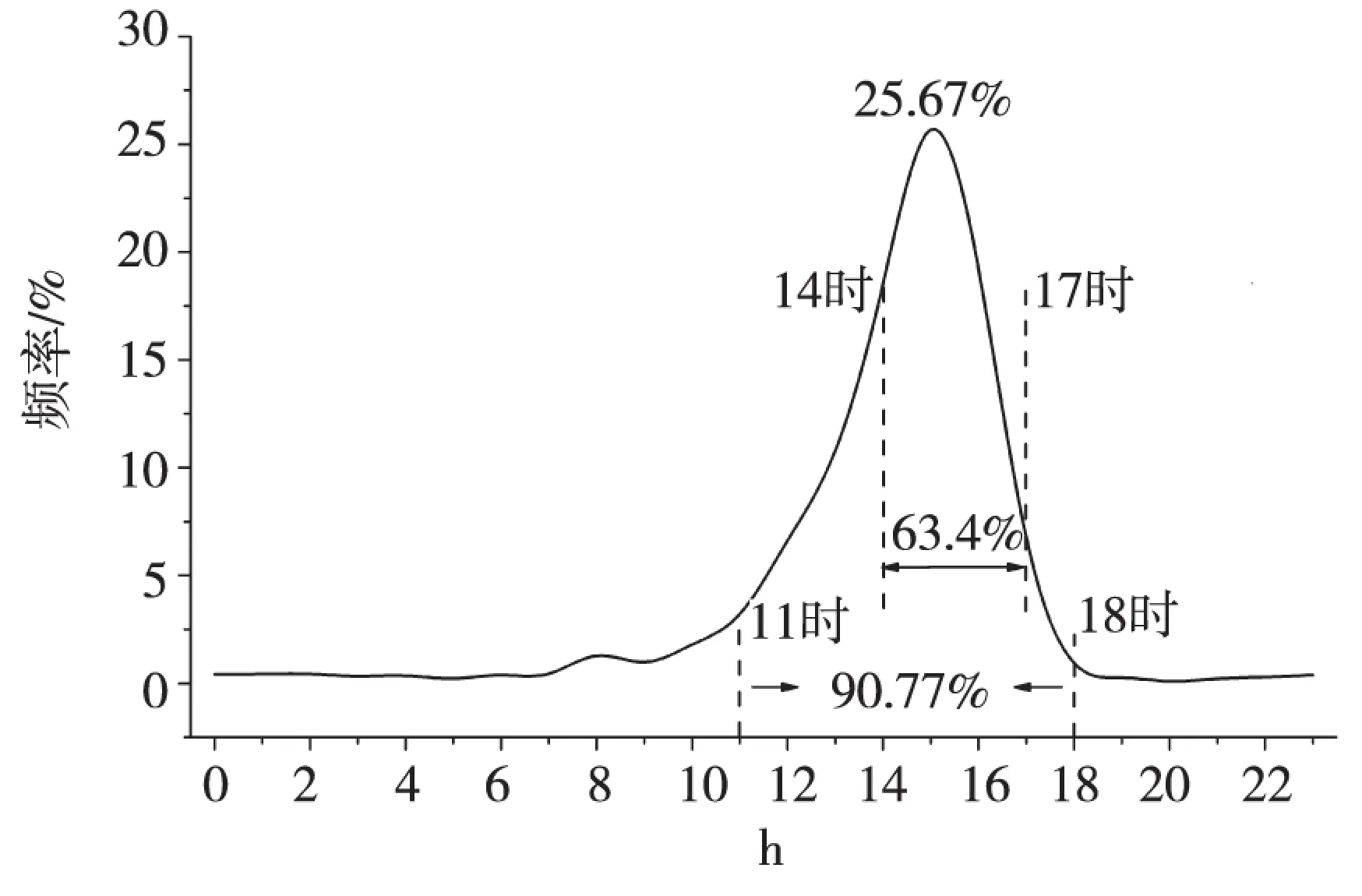
图4 怀化全市2015年日最高气温在全天各时段出现频率Fig.4 Frequency of Huaihua daily maximum temperature occurrence in each time period, 2015

4 气温预报订正

4.1 误差滑动平均值订正

假设ECMWF-thin对气温要素预报偏差具有一致性，利用模式起报前1～5 d最高气温预报与实况的误差计算前N日误差滑动平均值，本文选取1～5 d误差滑动平均值分别对ECMWF-thin日最高气温预报进行订正，从图5中可以看出，各预报时效的预报准确率均有不同程度的提升，预报准确率提升16%～20%不等，各预报时效的日最高气温预报利用滑动平均误差订正后都有明显的提升，对比所选取的各不同日误差滑动平均值订正效果，选取2～5 d误差滑动平均值作为订正值的并没有太大差别，订正后的最高气温预报准确率在54%～73%，尤其是前48 h日最高气温预报准确率超过65%，基本满足城镇预报要求。

图5 利用N日误差滑动平均值订正前后最高气温准确率Fig.5 Maximum temperature accuracy before and after using moving average of N days' deviation

4.2 天气类型订正

通过对ECMWF-thin日最高气温预报误差分析可以看出，模式预报主要是较实况偏低，但是简单的对模式预报进行上调，效果不理想，达不到日常预报要求，现根据不同天气类型(表1)，分别对不同时效的模式预报添加1～5 ℃，对订正前后的预报数据进行检验(图6)并进行讨论：

4.2.1 无降水天气条件下ECMWF-thin日最高气温预报订正分析 对于晴朗或少云(Ⅰ型a)， 模式预报的准确率随着预报订正值的增大，预报准确率逐渐升高，在订正值为4、5 ℃时，准确率开始下降，但都较未订正有较高提升；订正值为3 ℃时，00～24 h,24～48 h,48～72 h和96～120 h 4个时效达到最高值，分别为78.27%,75.50%,73.30%,67.03%，随着订正值的再次增加，高温预报准确率呈下降趋势；72～96 h订正值为4 ℃时，达到最高，为70.84%。

对于多云到少云(Ⅱ型a)在对模式日最高气温预报进行订正时，出现与Ⅰ型a天气类似的特征，在订正值为1、2 ℃时，预报准确率上升至55%～74%，00～24 h,24～48 h,48～72 h时效，较订正前，提高7%～12%，订正值为1 ℃时，准确率达到最大，之后准确率减小;72～96 h，96～120 h订正值为2 ℃时达到最大。

对于多云到阴天(Ⅲ型a)，各个时效的ECMWF-thin最高气温预报订正后的准确率走势不尽相同，00～24 h,24～48 h,48～72 h时效范围内，不订正或订正值为1 ℃时，准确率较高，之后随着订正值的增大准确率减小；而72～96 h和96～120 h时效，在订正值为1、2 ℃时，准确率较高。

图6 6种天气类型订正前后日最高气温预报准确率Fig.6 Daily maximum temperature forecast accuracy before and after revising with 6 kinds of weather types

总之，对于没有降水的天气，ECMWF-thin对地面2m日最高气温的预报需要根据具体天空状况添加1～4 ℃进行订正，订正后预报准确率均有所提升，尤其Ⅰ型a天气类型，提升明显。

4.2.2 有降水天气条件下ECMWF-thin日最高气温预报订正分析 对于少云有阵性降水(Ⅰ型b)的天气类型，模式自身预报准确率较低，且订正之后没有明显的提升。对于多云到少云有阵性降水Ⅱ型b的情况，订正值为1 ℃时，准确率有所升高，在56%～75%之间，之后随着订正值的增加，准确率逐渐下降。

对于阴天有雨(Ⅲ型b)，订正值选取1～5 ℃时，预报准确率呈下降趋势，为了更好的验证偏差，寻找恰当的值进行有效订正，所以将订正值范围扩大至-5～5 ℃。Ⅲ型b天气模式自身预报准确率在64%～80%之间，订正值后的曲线图如图6Ⅲ型b所示，呈抛物线形式，订正前预报准确率在波峰。

综上所述，对于有降水的天气，当天空状况为阴天(Ⅲ型b)时，模式自身预报准确率较高，订正效果差，但模式自身预报准确率较高，对于多云(Ⅱ型b)时，订正值为1 ℃时准确率有所提升，而对于少云(Ⅰ型b)时，模式自身预报准确率较低，且订正效果较差。

5 总结

①ECMWF-thin模式日最高气温预报准确率随着预报时效的延长而下降，单一时效内日最高气温预报准确率存在明显的月际变化，在不同预报时效内对全市11县日最高气温预报准确率有所差异，但整体变化趋一致，模式预报准确率普遍偏低，无法直接应用到实际业务中。

②ECMWF-thin日最高气温预报较实况以偏低为主，预报值低于实况值的占73%以上；导致模式出现这种误差的原因一是怀化自身的气候特点，再者，模式对地面2 m气温要素预报格式和怀化地区最高气温出现时段也直接导致这一结果。

③利用1～5 d误差滑动平均值对ECMWF-thin最高气温预报进行订正，不同日数误差滑动平均值对高温预报准确率订正差异较小，订正后的预报准确率在各时效范围内都有所提升，基本满足城镇日最高气温预报需求，且订正方法简单，操作方便。

④对不同天气类型的天气分类进行订正检验，发现对于没有降水的天气，模式预报需要根据具体天空状况添加1～4 ℃才能达到业务应用需求，而对于有降水的天气，需针对不同类型选取订正值。针对不同天气类型分类订正，整体效果好，尤其是对天空状况较好的天气，日最高气温预报准确率提高非常明显，但是此种订正方法虽然准确率提升明显，但是要以预报员对天气类型有较好的把握为基础。

[1] 周青,赵凤生,高文华. NCEP/NCAR 逐时分析与中国实测地表温度和地面气温对比分析[J].气象，2008，24(2):83-91.

[2] 李军，黄敬峰，游松财.不同空间尺度DEM对山区气温空间分布模拟的影响——以浙江省仙居县为例[J].地理科学,2012,32(11):1 384-1 390.

[3] 汪卫平,熊伟,陈余明.贵州省日最高气温气候特征分析[J].贵州气象,2013,37(1):7-10.

[4] 周婷婷,陈文惠.基于MODIS数据和气象观测数据的气温空间插值方法比较[J].地理科学进展,2011,30(9):1 143-1 151.

[5] 李莎,舒红,徐正全.利用时空Kriging进行气温插值研究[J].武汉大学学报,2012,37(2):237-241.

[6] 薛志磊,张书余.气温预报方法研究及其应用进展综述[J].干旱气象,2012,30(3):451-458

[7] 邱学兴,王东勇,朱红芳.乡镇精细化最高最低气温预报方法研究[J]. 气象与环境学报，2013，29(3):92-96.

[8] 周继先，聂云.思南县各乡镇气温分析及气温预报订正方法研究[J].贵州气象,2016,40(1):30-34.

[9] 陈晓燕, 赵玉金, 孙文英,等.支持向量机方法作温度预报试验[J],2006,30(1):31-33.

[10]张杰，罗岚心，韩晓令.CMIP5模式对长江流域气温模拟与预估[J],2014,38(2):15-18.

[11]刘宇,陈泮勤,张稳,等.一种地面气温的空间插值方法及其误差分析[J].大气科学，2006,30(1):146-152.

Analysis on daily maximum temperature forecast and revisal method in Huaihua District based on ECMWF intermediate-level resolution model

WANG Qiang,ZHANG Xiao,WANG Qihuan

(Huaihua Meteorological Observatory, Huaihua 418000, China)

Based on the ECMWF-thin forecast data of 2 meters above the surface temperature with the resolution of 0.125°×0.125° which were forecast from 20∶00, model forecast daily maximum temperature was calculated by the method of inverse distance weighted interpolating to 11 national meteorological stations of Huaihua. by amending the model forecast daily maximum temperature with the temporal and spatial characteristics of model forecast, the moving average of n days and synoptic classification method, the results show that the forecast accuracy declines in the forecast period extended which indicate remarkable monthly variations but no obvious spatial differences. The ECMWF-thin daily maximum temperature is generally lower than the actual daily maximum temperature. The forecast accuracy rose 16%～20% by the means of deviation moving average of n days, and the accuracy is about 54%～73% after revisal, and the whole procedure is convenient, simple and practical. Revised by the method of weather classification, the accuracy of all kinds of weather types has risen variously, especially for certain kinds. These two methods have their own advantages and disadvantages, both benefit the daily maximum temperature forecast.

temperature; revisal; moving average; weather types

1003-6598(2016)05-0032-06

2016-06-20

王强(1984—)，男，工程师，主要从事短中期天气预报及气象服务，E-mail:wangqiangxm@163.com。

P457.3

B