部分测量数据和无溢出二次模型修正问题的可解条件
2016-11-28罗海林张二喜
罗海林, 张二喜
(成都理工大学管理科学学院, 成都610059)
部分测量数据和无溢出二次模型修正问题的可解条件
罗海林, 张二喜
(成都理工大学管理科学学院, 成都610059)
针对三个系数矩阵都对称,质量矩阵非奇异和测量数据部分测得的二次模型修正问题,主要研究了它的可解性。首先,给出了该问题的研究背景和文献综述并提出一种特殊部分测量数据的二次有限元模型修正问题,给出两个重要引理,最后,采用矩阵分块法求得问题的可解条件。
二次模型;模型修正;无溢出现象;部分测量数据
引言
二次模型修正问题常出现在振动工程中,修正生成有限元模型的振动结构形式为:
(1)
其中,M0,C0和K0分别是质量矩阵,阻尼矩阵和刚度矩阵。系数矩阵M0,C0和K0满足二次束:
Q0(λ)=λ2M0+λC0+K0
(2)
其中,特征值λ与自然频率相关,特征向量是系统(1)的振型。系数矩阵M0,C0和K0满足线性代数系统:
M0XΛ2+C0XΛ+K0X=0
(3)
二次模型修正问题是从(M0,C0,K0)更新到(M,C,K),其中M0,C0,K0,M,C和K为对称矩阵,并且M0和M是非奇异矩阵。修正后的模型(M,C,K)满足:
MYΣ2+CYΣ+KY=0
(4)
MXΛ2+CXΛ+KX=0
(5)
其中,Λ=diag{Λ2,Λ3},X=[X2,X3],(Λ1,X1)为需要修正部分的特征对,(Σ,Y)为测量特征信息,(Λ,X)为保持不变部分的特征对。二次模型修正问题就是用测得的特征信息(Σ,Y)去替代原始的特征对(Λ1,X1),使得修正后的矩阵M,C,K满足(4)式和(5)式。
本文研究部分不完全测量数据和无溢出现象的二次有限元模型修正问题。在数学上,部分不完全测量数据和无溢出现象的二次有限元模型修正问题可以描述为:
问题I (二次模型修正问题)给定原始二次模型(M0,C0,K0),和少量相关特征对(Λ1,X1),在这里M0,C0和K0都是对称矩阵,Λ1∈Rp×p和X1∈Rn×p,p≤n。设新测得的特征对为(Σ,Y),在这里Σ∈Rp×p和Y∈Rn×p。修正二次模型(M0,C0,K0)到一个新的二次模型(M,C,K),使得:
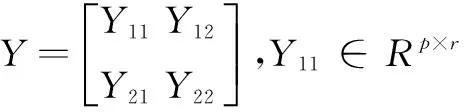
(2)(M,C,K)中其余的2n-p个特征对与原始模型(M0,C0,K0)中的保持一致。
在问题I中,(1)为部分测得数据条件,(2)为无溢出条件。修正后模型(M,C,K)满足方程(4)和方程(5),这就被称为部分测量和无溢出的二次模型修正问题。
文献[1]已经求解得出(M,C,K)参数表达式和西尔维斯特方程。文献[2]中采用近似逼近法求解二次模型修正问题。文献[3]用迭代算法解决无阻尼系统下的二次模型修正问题。文献[4]用迭代算法解决了二次模型修正问题。文献[5]用一种全新的方法求解无阻尼下的二次模型修正问题,同时保持修正后的模型正定和无溢出。文献[6]采用牛顿法研究了陀螺结构下的二次模型修正。文献[7]研究了阻力陀螺系统下的二次逆特征值问题。文献[8]用半正定规划技术研究结构二次逆特征值问题,该问题在理论和计算上都存在很大的难度。文献[9]主要讨论的是二次模型修正问题的无溢出现象。文献[10]主要研究的是二次模型修正问题的无溢出现象。特别的,对于无阻尼的二次模型修正问题总是可能满足无溢出条件。文献[11]研究的是基于梯度的迭代算法的陀螺系统的二次模型修正问题,给定系数矩阵M和K是对称正定矩阵和G是反对称矩阵。使得修正后的矩阵G和K分别近似逼近于G0和K0(为给定的初始矩阵),其中2p 引理1[1]给定测量特征对(Σ,Y)∈Rp×p,无溢出的二次有限元模型修正问题可解仅仅只要存在一个可逆矩阵T∈Rp×p和矩阵DΣ,使得 Y=X1T (6) (7) 这里 DΣ=YTCY+YTMYΣ+ΣTYTMY 引理2[1]如果(M,C,K)是无溢出的二次有限元模型修正问题的解,那么 (8) (9) (10) 其中Φ=ΦT∈Rp×p满足西尔维斯特方程 (Λ1-Θ)TM1+M1(Λ1-Θ) (11) 在实际情况中被测得的特征向量矩阵通常是不完全的,而且缺失形式多种多样。在这样的情况下也增加了问题求解的难度。 定理1设Yij(i=1,2;j=1,2)在问题I中已经被定义,Σ,Y11和Y22已测得并且rank(Y11)=r和rank(Y22)=p-r。当T1和T2线性无关,问题I可解当且仅当存在可逆矩阵T=[T1T2],其中 (12) (13) (14) 其中 证明 设Y=Yij(i=1,2;j=1,2),相应将X1和T分块为: T=[T1T2] 其中 X11∈Rp×p,X12∈R(n-p)×p,T1∈Rp×r,T2∈Rp×(p-r) 由(6)式,有: Y11=X11T1 (15) Y21=X12T1 (16) Y12=X11T2 (17) Y22=X12T2 (18) 因为X11可逆,由(15)式有(12)式成立。由(16)式和(12)式,有 (19) (20) 由(18)式有(13)式成立,由(17)式和(13)式,有 (21) 由(12)式知,因为rank(Y11)=r,所以有rank(T1)=r。同理,rank(T2)=p-r。又T1和T2线性无关,所以矩阵T可逆。设DΣ=DΣij(i,j=1,2),由(7)式得: (22) 所以得 证毕。 本文主要研究部分测量数据和无溢出现象的二次模型修正问题的可解条件。首先提出问题,然后给出该问题的可解条件。对于问题I仍有许多问题待完善,比如如何保持问题I的解正定,保持该问题正定的条件,这些都有待后续研究。 [1] KUO Y C,DATTA B N.Quadratic model updating with no spill-over and incomplete measured data:existence and computation of solution[J].Linear Algebra Appl.,2012,436(7):2480-2493. [2] KUO Y C,LIN W W,XU S F.New methods for finite element model updating problems[J].AIAA,Journal,2006,44(44):1310-1316. [3] YUAN Y X,LIU H.An iterative updating method for undamped structural systems[J].Meccanica,2002,47(3):99-706. [4] YUAN Y X,LIU H.An iterative updating method for damped structural systems using symmetric eigenstructure assignment[J].Journal of Computational and Applied Mathematics,2014,256(1):268-277. [5] MAO X B,DAI H.Finite element model updating with positive definiteness and no spill-over[J].Mechanical Systems and Signal Processing,2012,28(2):387-398. [6] XIAO X T,GU J,ZHANG L W.Quadratic model updating with gyroscopic structure from partial eigendata[J].Optim.Eng.,2013,14(3):431-455. [7] QIAN J,CHENG M S.Quadratic inverse eigenvalue problem for damped gyroscopic systems[J].Journal of Computational and Applied Mathematics,2014,255:306-312. [8] LIN M M,DONG B,CHU M T.Semi-definite programming techniques for structured quadratic inverse eigenvalue problems[J].Numer.Algor.,2010,53(4):419-437. [9] CHU M T,LIN W W,XU S F.Updating quadratic models with no spillover effect on unmeasured spectral data[J].Inverse Problems,2007,23(1):243-256. [10] CHU M,DATTA B,LIN W W.Spillover Phenomenon in Quadratic Model Updating[J].AIAA Journal,2008,46(2):420-428. [11] LIU H,YUAN Y.A gradient based iterative algorithm for solving model updating problems of gyroscopic systems[J].Applied Mathematical Modelling,2012,36(36):4810-4816. [12] YUAN Q.Dual approaches to finite element model updating[J].Journal of Computational and Applied Mathematics,2012,236(7):1851-1861. [13] YUAN Q.Matrix linear variational inequality approach for finite element model updating[J].Mechanical Systems and Signal Processing,2012,28(2):507-516. [14] XIAO X,GU J,ZHANG L.Quadratic model updating with gyroscopic structure from partial eigendata[J].Optim Eng.,2013,14(3):431-455. [15] YUAN Q.Proximal-point method for finite element model updating problem[J].Mechanical Systems and Signal Processing,2013,34(1-2):47-56. [16] YUAN Y,ZUO K.A no spill-over updating method for undamped structural systems[J].Applied Mathematics and Computation,2014,238(7):13-20. Solvability of Quadratic Model Updating Problems with Solvability of Quadratic Model Updating Problems with No Spillover and Partially Measured Data LUOHailin,ZHANGErxi (College of Management Science,Chengdu University of Technology, Chengdu 610059, China) Based on quadratic model updating problem of partially measurement data with three symmetric coefficient matrix and mass matrix nonsingular, the solvability of it is mainly studied. Firstly, the problems of the background, literature review and quadratic finite element model updating problems with a special partially measurement data are presented; then two important lemmas are given; finally, matrix partition method is used to obtain solvability conditions of the problem. quadratic model updating problem; no spillover; partial incomplete eigenvectors 2016-04-08 罗海林(1989-),男,四川南充人,硕士生,主要从事计算数学和二次模型修正问题方面的研究,(E-mail)18781946224@163.com 1673-1549(2016)04-0094-03 10.11863/j.suse.2016.04.20 O151;O321 A1两个重要引理

2二次模型修正问题的可解条件


3结束语
