基于塑性力学极限法的赵树岭滑坡稳定性分析

许忆

(浙江华东建设工程有限公司，浙江 杭州 310014)



基于塑性力学极限法的赵树岭滑坡稳定性分析

许忆

(浙江华东建设工程有限公司，浙江 杭州 310014)

基于塑性力学和极限分析理论，假设坡体处于极限滑动状态时，滑动面各处的岩土体均达到塑性极限状态，各段滑动面以及滑动面斜率改变处的竖直平面，都是速度间断面。在此基础上，通过虚功原理建立内外力功率平衡方程，由此求得基于塑性极限分析法的滑坡稳定性系数表达式。选取三峡库区赵树岭滑坡作为分析实例，根据塑性极限分析法的稳定性系数为1.14，计算结果表明赵树岭滑坡总体稳定，但稳定性富裕度不高。

滑坡；稳定性；塑性力学；极限分析

0 引言

极限分析是塑性力学求解结构破坏时承载能力的一个重要方法[1]。1975年，W.F.Chen将极限分析方法引入土力学的地基承载力、边坡稳定性和土压力分析，作出了开创性的工作[2]。

极限分析的基本出发点是假定结构的关键部位在外荷载作用下发生破坏，在该区域内各点均达到了极限平衡，处于塑性流动状态[3]。此时，荷载不增加，位移可以不断地发展。对于由岩土材料构成的滑坡，这一关键部位可以理解为是滑坡体。

该文基于塑性力学和极限分析理论，通过虚功原理建立内外力功率平衡方程，由此求得基于塑性极限分析法的滑坡稳定性系数表达式，并将该方法用于三峡库区赵树岭滑坡的实例研究中。

1 稳定性计算方法

当坡体处于极限滑动状态时，滑动面各处的岩土体均达到塑性极限状态，各段滑动面以及滑动面斜率改变处的竖直平面，都是速度间断面。在速度间断面的两侧，切向速度和发现速度均不连续。当各段岩土体的内摩擦角φ≠0时，沿各速度间断面上的岩土体应变速度vi与滑动面的切线方向有大小等于相应点处岩土的内摩擦角φi的夹角[4-6]。根据上述分析，可建立起滑坡滑动时的应变速度场，如图1所示。

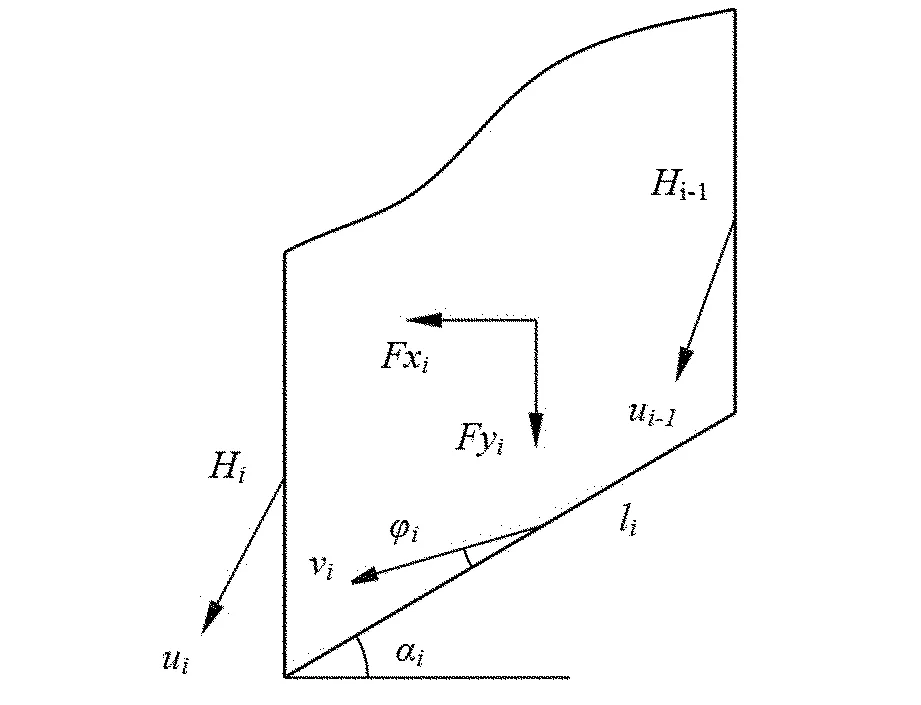
图1 滑坡体第i条块应变速度场示意图

对于c>0，φ>0的岩土体，由于岩土体具有相适应的流动法则，在剪切变形的同时，还会有体积膨胀，即所谓的剪胀效应。因此，变形单元内部的能量消散率可用下式表示：

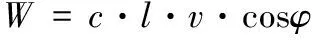
(1)

式中：c和φ为岩土体的粘聚力和内摩擦角；l为单元的宽度；v为岩土体的应变速度。

根据式1可得到沿整个滑动面岩土体内部的能量消耗率为：

(2)

式中：n为滑动面折线的段数；ci和φi为第i段滑动面处岩土体的粘聚力和内摩擦角；li为第i段滑动面的长度；vi为第i段滑动面处岩土体的应变速度。

沿各条块的竖向速度间断面，岩土体内部能量耗散率为：

(3)

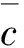
若不考虑其他形式的能量消散，则各速度间断面上总能量消散率为：

(4)

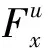
(5)

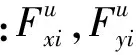
假设滑坡的稳定性系数为Fs，各块岩土体上的实际荷载为Fxi和Fyi，则有：

(6)

将式6代入式5中得：

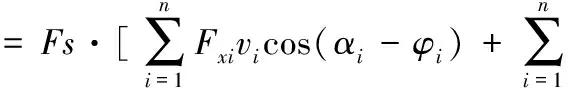
(8)

根据图1所示的第i块岩土体的应变速度关系图，可以得到滑动面上的应变速度vi,vi+1与两个相邻分块ui之间的竖向速度间断面上应变速度之间的关系，通过矢量计算，可得应变速度vi、vi+1和ui之间的关系为：

(9)

由此可得到度vi,ui与第一个块体滑动面处的速度v1之间的关系为：

(10)

将式10代入式8中，整理后可得稳定性系数Fs的表达式：

(11)

2 赵树岭滑坡稳定性分析

2.1 工程地质概况

赵树岭滑坡位于三峡库区巴东县云沱乡，赵树岭地区为三峡中段巫峡与西陵峡之间过渡地段，属宽谷地段。赵树岭及其邻近地区岩体褶皱轴线呈近EW走向，与斜坡的走向基本一致，因此斜坡以顺向坡为主。区内基岩岩性主要为三叠系巴东组T2b泥质灰岩、泥灰岩和粉砂质泥岩、粉砂岩，是三峡地区典型的易滑地层。

赵树岭滑坡为经过多次局部滑移和弯曲倾倒滑移而形成综合滑坡体。滑体平面上基本呈长方形，东西向宽度约550m，南北向长度约900～950m，面积约为5.0×105m2。赵树岭滑坡地形剖面呈缓坡与斜坡相间的折线形，地形总体平缓，坡角为15°～30°。赵树岭滑坡沿主滑方向的长度约为950m，滑体表面总体呈台阶状，高程150～200m之间为第一级缓坡平台，高程200～350m之间为陡坡，高程350～400m之间为第二级缓坡平台，400m以上为较陡的滑坡后缘。通过地质勘探确定滑动面的空间位置，滑动面总体平缓，滑体厚度为40～65m左右，滑动面在前缘剪出口呈反翘状。赵树岭滑坡概化模型如图2所示。

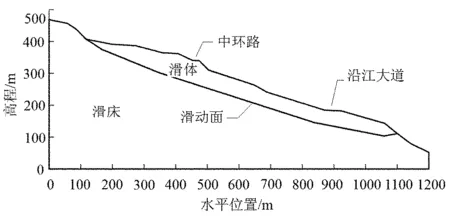
图2 赵树岭滑坡概化模型示意图

赵树岭地区物质结构也是由表层崩滑体层向完整基岩逐渐过渡。滑坡区物质总体上可分为2大层,即表层崩滑体层和基岩。表层崩滑体层主要由岩体经滑移形成的块裂、碎裂岩、含泥碎块石及碎块石组成，主要来源于巴东组第三段T2b3。基岩则以巴东组第二段T2b2紫红色粉砂质泥岩、泥质粉砂岩为主[7]。滑坡区出露的巴东组第三段地层中可见多层软弱破碎带，这些破碎带具有不顺层、不连续、厚度变化大等特点。

2.2 几何及物理力学参数

将滑动面斜率改变处作为划分条块的间断点，将赵树岭滑坡划分为8个条块，条块划分示意图及其编号如图3所示，各条块的几何参数见表1。

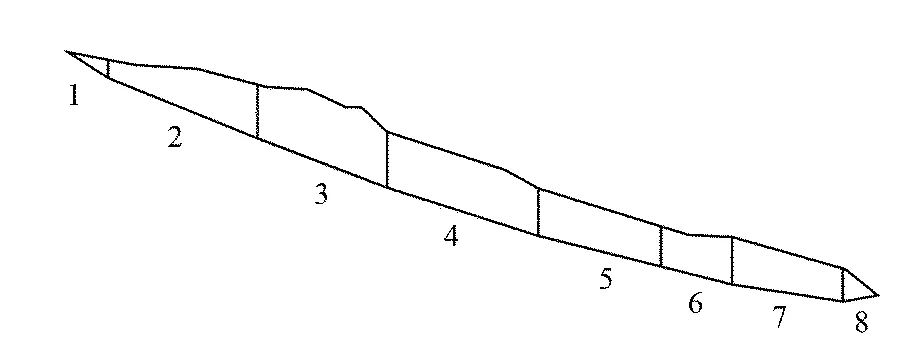
图3 赵树岭滑坡条块划分示意图

编号面积/m3宽度/m高度/m角度/(°)1539．8057．8922．253328434．23195．7165．5822312194．20165．2558．0121412204．59192．4947．821857961．55156．3749．081564375．7687．8352．791476588．06136．8040．3098895．6143．39—10

根据室内试验和工程地质类比法确定赵树岭滑坡中滑体、滑带和滑床的物理力学参数见表2。

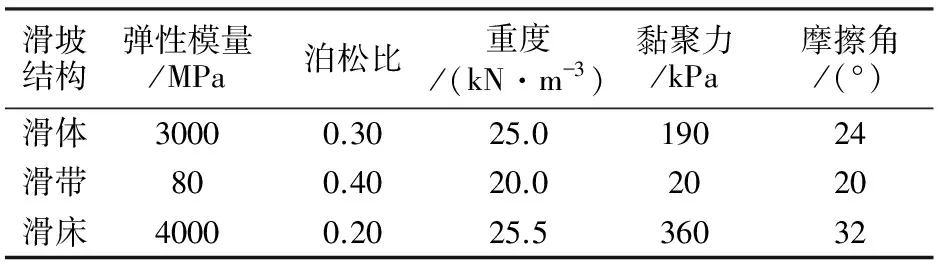
表2 赵树岭滑坡计算模型物理力学参数

2.3 计算结果对比

根据赵树岭滑坡的几何及物理力学参数，采用该文提出的稳定性计算方法开展赵树岭滑坡的稳定性分析，即采用式(11)计算稳定性系数。为了进行对比分析和验证说明，同时也采用目前通用的滑坡稳定性计算方法开展平行计算，采用的通用稳定性计算方法为Morgenstern-Price法、Ordinary法、Bishop法和Janbu法，计算结果如表3所示。

表3 赵树岭滑坡各方法计算结果对比

从表3可以看出，5种计算方法的结果分布在1.14～1.29之间，说明赵树岭滑坡总体稳定，但稳定性富裕度不高，在库水、降雨和其他扰动因素的作用下，其稳定性有可能进一步降低。5种计算方法中，Bishop法的计算结果最高为1.29，该文提出的塑性极限法最低为1.14。根据实际地址调查，赵树岭滑坡自形成以来，经历过暴雨、地震等工况未发生整体失稳，说明该滑坡的总体稳定性尚好，因此其稳定性系数应该大于1.0。但滑坡体内已发现5处小型崩滑体，规模一般数百至数千方不等，滑体厚度一般几十厘米至几米不等，主要分布于中环路及沿江大道内侧开挖边坡及冲沟或长江岸边陡坡处，说明滑坡体虽然总体稳定，但其稳定性富裕度不高。而该文提出的塑性极限法的计算结果为1.14，较其他各种计算方法更为符合实际情况。由此验证了该文提出的塑性极限法的计算结果是基本可信的，说明该方法具有一定的适用性和可行性。

3 结论

(1)通过弹塑性力学的虚功原理建立滑坡体内外力功率平衡方程，由此求得基于塑性极限分析法的滑坡稳定性系数表达式。

(2)将选取三峡库区赵树岭滑坡作为分析实例，根据塑性极限分析法的稳定性系数为1.14，计算结果表明赵树岭滑坡总体稳定，但稳定性富裕度不高，在库水、降雨和其他扰动因素的作用下，其稳定性有可能进一步降低。

(3)对比分析塑性极限分析法和通用常规稳定性计算方法的结果，发现塑性极限分析法较其他方法更为符合实际情况。因此，塑性力学的极限分析方法不仅在土力学的地基承载力、边坡稳定性和土压力分析这三个领域的运用可以运用，也可以在大部分的岩质滑坡稳定性分析中得以运用。

[1] 陈祖煜,汪小刚,杨建等.岩质边坡稳定分析[M].北京:中国水利水电出版社,2005.

[2] Chen W F. Limit analysis and soil Plasticity[M]. Amsterdam: Elsevier, 1975.

[3] 李同林,殷绥域.弹塑性力学[M].武汉:中国地质大学出版社,2006.

[4] 赵法锁.坡体平面旋转机理及稳定性研究[M].西安:西安地图出版社,1999.

[5] 刘汉东.边坡位移矢量场与失稳定时预报试验研究[J].岩石力学与工程学报,1998,17(2):111-116.

[6] 王根龙,伍法权,李巨文.折线型滑面边坡稳定系数计算的极限分析上限解[J].水文地质工程地质,2007,34(1):62-65.

[7] 唐辉明,马淑芝,刘佑荣,等.三峡工程库区巴东县赵树岭滑坡稳定性与防治对策研究[J].地球科学,2002,27(5):621-625.

Stability Analysis of Zhaoshuling Landslide Based on Plasticity Mechanics Limit Method

XU Yi

(Zhejiang Huadong Construction Engineering Limited Corporation, Zhejiang Hangzhou 310014, China)

It is assumed that sliding surface of landslide achieves the plastic limit state when it is in the state of extreme sliding based on plastic mechanics and limit analysis theory. All of the sliding surface and vertical planes of slope change part of sliding surface are all velocity discontinuity surfaces. On this basis, internal and external force power balance equation is established by the principle of virtual work, and then the expression of landslide’s factor of stability is obtained based on the plastic limit analysis. The Zhaoshuling landslide in the three gorges reservoir region is selected as the case study, and the factor of stability of the Zhaoshuling landslide is 1.14 according to the plastic limit analysis method, the calculation results show that Zhaoshuling landslide is generally stable, but the stability is not very enough.

Landslide; stability; plastic mechanics; limit analysis

2016-07-25；

2016-08-01；编辑：曹丽丽

许忆(1962—)，男，高级工程师，主要从事水利水电工程勘察及地质灾害防治研究工作；E-mail：xu_y@ecidi.com

TU443

B

许忆.基于塑性力学极限法的赵树岭滑坡稳定性分析[J].山东国土资源，2016,32(10)：75-78.XU Yi. Stability Analysis of Zhaoshuling Landslide Based on Plasticity Mechanics Limit Method[J].Shandong Land and Resources, 2016,32(10)：75-78.