P气田基于地质模型的储量不确定性分析

高玉飞，胡光义，王晖，孙立春

(中海油研究总院，北京 100027)



P气田基于地质模型的储量不确定性分析

高玉飞，胡光义，王晖，孙立春

(中海油研究总院，北京 100027)

地质建模的最终目的是建立反映地质认识的地质模型，并对储层的不确定性以及由此带来的储量不确定性进行定量表征。南海P气田正处于开发的前期研究阶段，井点资料少，储层的纵横向变化快，储量不确定性强。该文以地质模型为载体，探讨了该气田地质储量不确定性分析的方法，总结了相似气田地质储量不确定性分析的一般方法：通过对变量的敏感性分析，确定影响该气田地质储量的主要变量，以此为基础通过拉丁超立方概率分析法进行储量评价及地质模型的优选，最终确定构造和气水界面的变化是影响该气田储量的主要因素，P50是该气田可动用储量。该方法为前期研究阶段的储量动用提供了新的思路。

地质模型；变量；不确定性分析；地质储量；拉丁超立方法

0 引言

P气田位于番禺低隆起南部，白云凹陷北坡第二排北掉的反向断裂带上，为复杂断块型气田，主要气藏都发育了东、西2个构造高点。各目的层高点埋深-3110.0～-3160.0m，圈闭面积为7.60～16.60km2，主要含气层系是新近系下中新统珠江组下部。目前该气田处于前期研究阶段，只有两口钻井，加之地震资料品质相对较差，储层认识不清，地质储量不确定性强。因此，地质储量影响因素及储量动用规模的确定成为该气田开发中需要解决的首要问题。

油气田开发过程中，从初期的储集层地质基础研究到建立三维静态储集层地质模型都包含许多不确定性[1-3]。以往对储量的不确定性研究中，通常采用在某一确定的地质概念模型基础上，通过改变其种子数的方法产生多个实现，并对这些实现中的不确定性给予定性评价及模型优选或采用算术平均进行简单的概率计算[4]。但是这种方法带有明显的局限性，因为它忽略了地质参数本身的不确定性对储量造成影响的本质，而偏向于数学统计的结果；其次从模型的等概率实现中无法优选合适(既接近真实，又反映风险)的模型进行油藏数值模拟。

近年来，随着储层不确定性分析的不断发展，地质模型在储量计算过程中造成的储量不确定性分析受到了很多专家的关注，越来越多的地质工作者开始关注地质参数引起的储量不确定性，例如：吴健祥[5]通过对岩相模型的不确定性研究分析了某地区储量的不确定性；霍春亮[6]等人在分析渤海湾某油田时在充分分析地质模型的基础上，结合蒙特卡洛法进行储量不确定性的分析；孙立春[7]等人则利用数学方法分析了某气田孔隙度以及含水饱和度对储量的不确定性的影响。

综上所述，在基础资料匮乏、地质因素复杂的地区，单一一种方法分析储层的不确定性已经捉襟见肘，特别是针对海上油田，在利用地质模型计算储量的不确定性分析中考虑的因素必须扩展到建模过程中参数的合理选取。鉴于此，该文从影响地质储量基础地质参数入手，逐一分析各个参数本身的不确定性，结合合理的数理统计，综合探讨影响储量的各种地质参数的敏感性，从而提出合适的计算模型并确定动用储量规模。

1 地质参数分析

影响储集层地质模型的不确定性变量很多，但是对储量的影响程度又各有不同，因此需要分析各个变量对储量的敏感性。

该次研究遵循只探讨与地质模型有关的变量，从建模过程中选择变量的原则。在P气田的建模过程主要存在构造因素、气水界面、孔隙度的变程、孔隙度下限值以及含气饱和度等5个不确定性的变量。以下就各个变量的取值范围分述之。

1.1 构造因素

建模软件对与构造不确定性的分析是以设定不同层位的偏差进行的，即选取目的层位构造解释的变化范围，以其偏差作为变化幅度，随机取值建立构造模型，所以偏差往往设置成误差范围的一半。

(1)

式中：Sr—建立的构造层面值(m)；Sbc—初始构造值(m)；U1s—初始值的偏差，可为一个面也可为一个常数(m)；Usgs—以0为均值1为偏差的一个正态分布值，常数。

P气田地区几个相关气田的地震资料品质低，造成地质层面的解释存在很大的不确定性(表1)。综合P气田和其相邻P2气田各井实钻深度与叠前偏移深度的偏差，2个气田各井偏差的平均值为30m。因此将构造因素研究的偏差幅度设为15m。

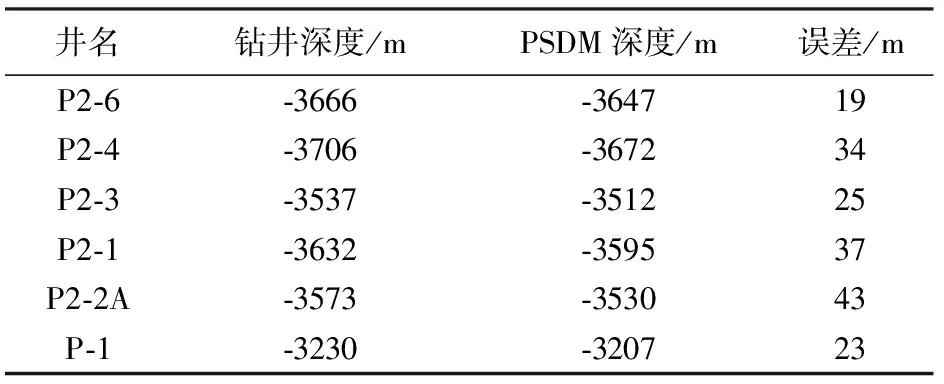
表1 实钻深度与叠前偏移深度(PSDM)偏差

1.2 气水界面

在没有钻到气水界面的气层，往往通过测井的气底界面或者压力测试来确定气水界面，这样必然导致气水界面的不确定性。测井解释P-1井ZJ组气层的气底是-3227.2m，FMT外推气水界面是-3252m，因此确定气水界面的不确定性范围为-3252～-3227.2m。

1.3 孔隙度的变程

变差函数反映了空间某一方向上两点变量的相关性，而变程就是反映这个相关性的最大距离，不同方向上变程不同，空间上最大变程的方向即为变差函数的主变程的方向，与此方向垂直的方向上的变程称为次变程。在资料比较充足的情况下，往往通过井点数据的实验变差函数的分析，确定变差函数的主方向以及变程的大小[8]。

从地质的角度来看，相建模的过程中，平面上与物源平行的方向往往是沉积相延伸范围最广、分布最稳定的方向，也是相关关系最好的方向，即主变程的方向。该区基础资料少，地震资料品质差，从现有的资料中很难通过实验变差函数的分析确定合适的孔隙度变程及其方向，考虑到沉积相是影响储层孔隙度的主要因素，因此在孔隙度模拟的过程中，利用沉积相与孔隙度潜在的关系，通过分析沉积相来确定孔隙度的变程的设置，以沉积相或者砂体的展布范围作为设置变程的基础[5-8]。

P气田ZJ组属于低水位沉积期，以海相滨岸砂岩沉积为主，滨岸砂岩滨岸沉积相的延伸范围在很大程度上受控于海岸地貌特征，物源方向与岸线往往垂直，因此当时沉积的滨岸坡折带的长度可以近似为沉积相沿物源方向的变化范围[9-13]，由此来确定滨岸砂岩的孔隙度的主变程范围，结合前人的研究成果[9-13]，确定变化范围是3000～6000m。次变程的确定一是考虑到在变差函数中一般小于主变程，再从沉积的角度次变程要控制整个气田的1井区，因此其变化范围设置为2400～4800m。

1.4 含气饱和度

由于井点值与等值线面积权衡值之间存在一定的差异，前者计算值为54.6%，后者为55.6%，因此设置含气饱和度的变化范围为54.6%～55.6%。

1.5 孔隙度下限

在P气田，实验岩心的分析取心气层孔隙度的最低值是9%，从累积烃柱与孔隙度的关系图上看(图1)，该区累积烃柱是从孔隙度为6%开始才出现明显的变化，因此确定6%～9%为孔隙度下限的变化范围。

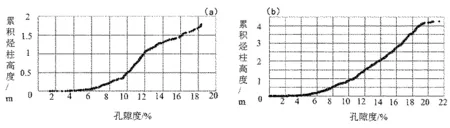
(a)P-1井孔隙度；(b)P-2井孔隙度图1 P-1和P-2井累积烃柱高度与孔隙度关系图

2 敏感性分析

确定了变量的取值范围，使用Petrel软件的不确定性分析模块，进行各个变量对储量影响的敏感性分析。该次变量敏感性分析采用的思路是：只变化一个变量，固定其他变量不变，观察储量的变化情况，通过对储量结果的统计，计算变量对储量的相对影响。相对影响的计算是以最小值与平均值的差值除以平均值为负影响，以最大值与平均值的差值除以平均值为正影响，做出敏感性分析图[7]。

对每个变量进行100次实现，分析其敏感性(表2、图2)，含气饱和度和变程对储量的相对影响都小于5%，影响结果小，不是储量的主要影响因素。孔隙度的下限值对储量的相对影响为6%～7%，这是一个值得考虑的因素。气水界面的影响因素较大，为14%～20%，这是因为气水界面的变化影响了岩石体积，从而引起孔隙体积也发生较大的变化，造成储量变化范围增大。构造因素是P气田ZJ30-2组最大的影响因素，其相对影响达到了50%左右，由此可见，构造在储量评价中存在较大的风险。通过以上分析，可以看出构造因素、气水界面、孔隙度的下限值是P气田ZJ组3个重要的影响因素，可以作为下一步分析的变量。

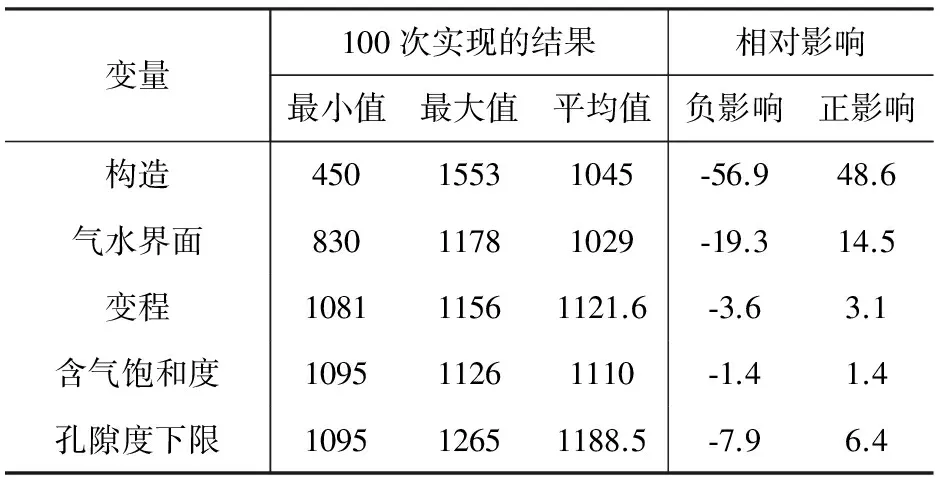
表2 各变量敏感性分析

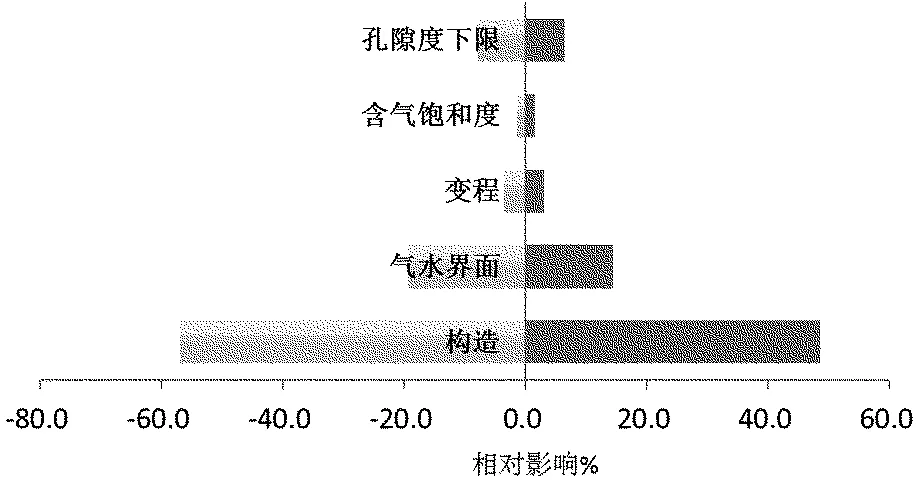
图2 P气田ZJ组不确定性因素敏感性分析

3 储量评价及模型优选

对储层参数进行敏感性分析的目的是为了进行储量计算，确定储量的风险和潜力，并挑选合适的模型提供给下一步的数值模拟[5-8]。在储量评价过程中通常采用蒙特卡洛法进行储量概率的计算，但是这种取样方法在取样次数不够充足的情况下，取值一般聚集在中值附近(图3a)，该文采用拉丁超立方取样法进行对比。

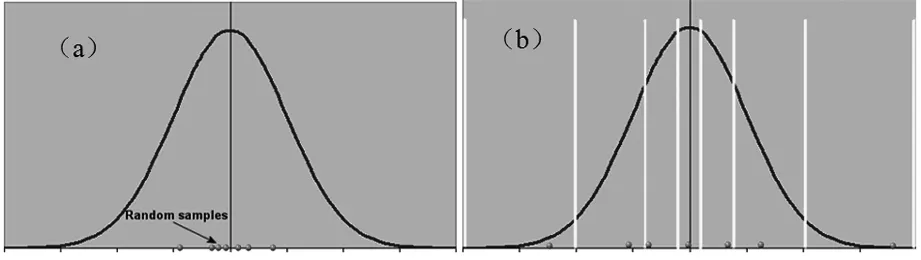
(a)蒙特卡洛取样；(b)拉丁超立方取样图3 两种取样方法比较

拉丁超立方取样法根据设置的运行次数将变量的分布范围分为几个等概率的区域，运行多少次就会设置多少个区域(图3b)。每一次取样都是随机的从一个等概率区域内选择一个值，下一次取样就会到下一个等概率区域进行取值。与蒙特卡洛法相比，这种方法取样的区间更广，所以也就更能突出变量的不确定性。

在储量计算中采用概率储量的概念，概率储量不仅能提供更准确的储量计算结果，还能更好的描述储量的不确定性，因此可以获得关于储量的准确判断，从而更合理地评价储量的风险和潜力[9-10]。

利用优选的3个变量，采用拉丁超立方的取样方法进行150次实现。在150次实现后，根据储量累积概率分布图求出3个概率储量P10为3.396、P50为7.503、P90为14.517，分别称为“悲观”、“最可能”和“乐观”储量。

一般认为，一个油(气)藏的真实储量(或称为实际储量)是不可能精确预测并求得的[11-17]。然而，概率密度曲线可以反映这个真实储量落入某一区间的可能性。真实储量大于P90的概率只有10%，说明P90是相对乐观的估计。相反，真实储量小于P10的可能性只有10%，说明P10是相对有把握的估计。P50表示大于和小于真实储量的可能性都是50%。

该次模拟的P50为7.503×108，与容积法计算值相比(表3)，其小于探明与控制储量之和而大于探明储量，进一步说明了它的可靠性。由此选择P50作为该次模拟的最佳值，推荐作为油田开发的动用储量并挑选出该值所对应的模型，作为提供给油藏进行下一步分析的地质模型。

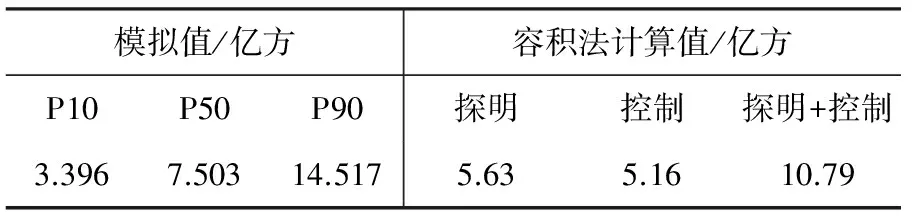
表3 模拟值与容积法计算值比较

4 结论

(1)通过对各个变量的敏感性分析，确定了P气田储量的主要影响因素：构造因素、气水界面、孔隙度下限值，其中构造因素对储量的影响最大。

(2)由于各个影响因素的不确定性较强，对于P气田的不确定性分析，采用拉丁超立方的取样方法，取样的区间更广，更能突出各个因素的不确定性。

(3)P气田不确定性分析的结果表明，该次模拟的P50是最佳值，大于探明储量而小于探明储量与控制储量之和，相对风险最小，又考虑了部分潜力，可推荐作为油田开发的动用储量，该P50所对应的地质模型，可作为开发方案编制的推荐模型。

[1] Tyler K J，Omdal S．Faster history matching and uncertainty in predicted production profiles with stochastic modeling[A]． SPE26420， 1994：100-110.

[2] 姜汉桥,谷建伟,陈民锋,等.时变油藏地质模型下剩余油分布的数值模拟研究[J].石油勘探与开发,2005,32(2):91-93．

[3] 裘怿楠，贾爱林．储层地质模型10年[J]．石油学报，2000，21(4):101-104．

[4] 李少华,张昌民,彭裕林,等.储层不确定性评价[J].西安石油大学学报(自然科学版),2004,19(5):16-20.

[5] 吴建祥.一种地质模型不确定性分析的新方法[J].内蒙古石油化,2008,34(20):16-17.

[6] 霍春亮,刘松,古莉,等.一种定量评价储集层地质模型不确定性的方法[J].石油勘探与开发,2007,34(5):574-579.

[7] 孙立春，高博禹，李敬功．储层地质建模参数不确定性研究方法探讨[J]．中国海上油气，2009，21(1)：35-38.

[8] 吴胜和，金振奎，黄沧钿．储层建模[M]．北京:石油工业出版社,1999：9-11.

[9] 郑荣才，郑哲，高博禹，等.珠江口盆地白云凹陷珠江组海底扇深水重力流沉积特征[J].岩性油气藏，2013，(2)：2-8.

[10] 朱筱敏，黄捍东，代一丁，等.珠江口盆地番禺4洼文昌组层序格架与沉积体系研究[J].岩性油气藏，2014，(4)：1-8.

[11] 乔博，张昌民，杜家元，等.珠江口盆地浅水区和深水区重力流沉积特征对比[J].岩性油气藏，2011，(2)：59-63.

[12] 耿威，郑荣才，魏钦廉，等.白云凹陷珠海组储层沉积学特征[J].岩性油气藏，2008，(4):98-104.

[13] 邢文礼，张尚锋，杜家元，等.稀疏井网条件下利用测井曲线识别层序界面方法探讨——以珠江口盆地珠江组为例[J].岩性油气藏，2010，(2):111-114.

[14] 徐钟济．蒙特卡罗方法[M]．上海:上海科学技术出版社，1987：261-291.

[15] 宋立新,陈超,赵庆辉.已探明未动用储量评价方法研究[J].特种油气藏，2001，8(2)：46-50.

[16] Gair R．Integrating deterministic and probabilistic reserves[A]．SPE 82000， 2003：1-7.

[17] 王振国，杨仁超，路中奇，等. 苏里格气田西区S47区块石盒子组八段沉积微相[J].山东国土资源，2014，30(3)：38-43.

Analysis on Uncertainty of Reserve Based on Geology Model in P Gas Field

GAO Yufei，HU Guangyi，WANG Hui，SUN Lichun

(CNOOC Research Institute, Beijing 100027, China)

The ultimate goal of geological modeling is to set up a reasonable geological model and characterize the uncertainty of reservoir and reserves. The South China Sea P gas field is at the stage of early study and its well data is lack, the lateral and vertical variety of reservoir is very quick, so the uncertainty of the reserve is very strong. This paper discussed the method for the uncertainty of reserve based on geology model, then the general method about the uncertainty of similar gas field has been summarized. Through analysis on the sensitivity about the variable, the main variable has been determined. Based on this study, reserve evaluation and optimization of geological model have been done by Latin Hypercube Sampling. At last the change of structure and OWC is defined as the main factor affected the reserve of the gas field, and P50 is the producing reserve. The method provide a new thought for reserve utilization at the stage of early study.

Geological model； variable；analysis on uncertainty；geological reverse；Latin Hypercube method

2016-03-30；

2016-08-06；编辑：王敏

国家重大专项基金项目，项目编号为2011ZX05024-001作者简介：高玉飞(1983—)，男，山东胶州人，工程师，主要从事石油开发地质工作；E-mail：215954707@qq.com

TE155

A

高玉飞，胡光义，王晖，等.P气田基于地质模型的储量不确定性分析[J].山东国土资源，2016,32(10)：16-20.GAO Yufei，HU Guangyi，WANG Hui，etc. Analysis on Uncertainty of Reserve Based on Geology Model in P Gas Field[J].Shandong Land and Resources, 2016,32(10)：16-20.