粒子群神经网络在大跨钢结构挠度监测中的应用

肖兴国，袁长征，李超

(1.重庆市勘测院，重庆 401121； 2.重庆市智能感知大数据产业技术协同创新中心，重庆 401121)



粒子群神经网络在大跨钢结构挠度监测中的应用

肖兴国1*，袁长征1，2，李超1，2

(1.重庆市勘测院，重庆 401121； 2.重庆市智能感知大数据产业技术协同创新中心，重庆 401121)

针对传统BP神经网络拓扑结构不确定、收敛效率低、容易陷入局部最优解的缺陷，引入粒子群(PSO)算法替代BP神经网络中基于误差函数梯度下降的学习训练规则，构建了粒子群神经网络(PSO-BP)模型，并以重庆某大型场馆安全监测项目为例，通过对比分析验证了粒子群神经网络模型在大跨钢结构挠度监测中的可行性以及与传统BP神经网络模型相比在效率和精度方面的优越性。

BP神经网络；粒子群算法；大跨钢结构；挠度监测

1 引 言

现代社会中，各种大型场馆如机场、体育馆、会展中心等是人类生活的重要场所，而大跨钢结构是这些建筑常用的结构形式之一。钢结构在服役过程中由于受外部环境干扰、偶然超载、长期疲劳积累以及自身缺陷[1]等因素影响，容易发生挠度变形，严重时可能危及人们的生命财产安全，因此需要定期对其进行挠度监测并对变形趋势进行分析预测。由于大跨钢结构的挠度变形往往由多种因素造成，且每种因素对变形的影响大小以及与变形量之间的关系各不相同，要建立顾及各种影响因子的非线性数学模型比较困难。

BP神经网络是一种基于误差反向传播算法的神经网络模型，具有分布式存储和并行处理、自学习、自适应等特点，有很强的非线性处理能力[2]，因此在变形监测数据分析与预测中得到了广泛应用[3～8]。

传统的BP神经网络算法存在网络拓扑结构不确定、迭代收敛效率低、容易出现局部最优解等缺陷[9]，需要对其进行改进和优化以满足复杂多变的监测数据分析要求。粒子群算法是一种新型的智能优化算法，具有原理简单、所需参数少、收敛速度快等特点[10]。采用粒子群算法代替传统BP神经网络模型基于梯度下降的学习算法，形成粒子群神经网络(PSO-BP)，有效改善了神经网络的性能。

2 PSO-BP神经网络模型的构建

2.1 BP神经网络基本原理

BP神经网络是基于误差反向传播算法的一种多层智能感知器模型，是迄今为止应用最为广泛的神经网络[11]。以三层BP网络为例，其模型结构如图1所示：

图1 三层BP神经网络结构图

图中Xk表示输入层的输入因子；Vj表示隐含层的输出因子；Oi表示输出层的输出因子；ωjk表示输入层节点与隐含层节点间的连接权；ωij表示隐含层与输出层间的连接权；N、L、M分别表示输入层、隐含层和输出层节点的数量。

BP神经网络的基本算法思想是：模型输入层把输入因子传递给中间层，中间层经过处理之后，产生一个输出因子传递给输出层，这一过程叫做误差的正向传播；然后将模型的输出因子与期望的输出因子进行比较，若误差大于设定的阈值，则进入误差的反向传播过程，即将误差信号沿原连接路线返回，并采用梯度下降算法修改各层神经元之间的连接权值和阈值使误差减小；重复正向传播和反向传播过程，直到误差小于设定值，则训练结束。2.2 粒子群算法基本原理

粒子群算法是Kennedy和Eberhart[12]受人工生命研究结果的启发、通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法[13]。该算法将每个样本看作n维空间上的一个点，即“粒子”，粒子以一定的速度在空间中运动，每个粒子都有一个由目标函数决定的适应值，并记录了自身到目前为止使适应值最优的最好位置和当前位置，即粒子自己的运动经验。粒子根据自身及其他粒子的运动经验动态调整速度和位置，直到适应值达到目标。算法的数学描述如下：

设在n维空间中，有m个粒子构成种群X={X1，X2，…，Xm}，其中第i个粒子的当前位置为Xi={xi1，xi2，…，xin}；当前速度为Vi={vi1，vi2，…，vin}；其经历的个体最好位置为Pi={pi1，pi2，…，pin}；种群内所有粒子经历的全局最好位置为Pg={pg1，pg2，…，pgn}。设粒子的目标函数为f(x)，且函数值越小代表位置越优，则第t次迭代时粒子的当前最好位置由式(1)决定：

(1)

种群的全局最好位置由式(2)决定：

(2)

基于以上定义，粒子群算法的进化方程可以表示为：

vij(t+1)=vij(t)+c1r1(t)[pij(t)-xij(t)]

+c2r2(t)[pgj(t)-xij(t)]

(3)

xij(t+1)=xij(t)+vij(t+1)

(4)

其中，i表示第i个粒子；j表示该粒子的第j维；t表示第t次迭代；c1、c2分别为个体学习因子和全局学习因子，通常均取2；r1、r2∈[0，1]是两个独立的随机数；xij∈[-xmax，xmax]，vij∈[-vmax，vmax]分别表示粒子的位置和速度。

2.3 PSO-BP神经网络模型

BP神经网络的学习训练过程就是不断调整更新神经元的阈值以及神经元之间的连接权值使误差减小，因此可以将模型中哥神经元的阈值和连接权值作为粒子群算法中粒子的位置属性，而将模型输出与期望输出间的平方误差作为粒子的适应值，然后通过粒子群算法来优化神经网络的阈值和权值，直到误差满足要求。

以三层神经网络为例，假设输入层、隐含层以及输出层的神经元个数分别为N、L、M；隐含层和输出层神经元阈值分别为θj、θi；输入层与隐含层、隐含层与输出层之间的连接权值分别为ωjk、ωij，粒子群由T个粒子构成X={X1，X2，…，Xt，…，XT}，则粒子t的位置属性可表示为：

Xt={θj、ωjk、θi、ωij}，k=1，2.，..，N；j=1，2，…，L；i=1，2，…，M

(5)

首先将粒子群进行初始化，输入样本数据计算得到模型输出Oit，然后计算期望输出与模型输出的均方误差，并将其作为判断粒子位置属性优劣的适应值，即粒子的目标函数为：

(6)

其中，P为样本数据总数，M为每个样本的输出数据个数。

通过粒子群算法的迭代更新来优化神经网络模型的阈值和连接权值，直到误差满足要求。算法的具体步骤如下：

(1)初始化神经网络模型的拓扑结构，包括模型的层数(一般为3层)以及各层神经元个数；

(2)确定粒子群的种群规模m和每个粒子的维度n。粒子的维度n等于神经网络中所有阈值以及连接权值的总和，m个粒子就代表m组不同的阈值和连接权值。

(3)随机初始化粒子群的位置和速度矩阵，并将每个粒子的当前位置作为其个体最优位置Pbest。

(4)输入样本数据，根据每个粒子位置属性所代表的阈值和连接权值计算模型输出，然后按照式(6)计算所有样本的模型输出与期望输出间的均方误差平均值，将其作为该粒子的适应值，并将适应值最小的粒子所对应的位置作为种群的全局最优位置Gbest。

(5)判断Gbest的适应值是否满足要求，若满足则训练结束，Gbest的位置即为神经网络最终的阈值和连接权值，否则继续步骤(6)。

(6)按照式(3)和式(4)更新各粒子的速度和位置，重新计算粒子的适应值。

(7)将粒子的当前适应值与个体最优位置Pbest的适应值进行比较，若更小，则用当前位置替换Pbest。

(8)将所有粒子的Pbest的适应值与全局最优位置Gbest的适应值进行比较，若更小，则替换Gbest。

(9)若Gbest的适应值满足要求或迭代次数达到设定的上限，则训练结束，Gbest的位置即为神经网络模型最终的阈值和连接权值，否则返回步骤(6)继续训练。

算法的基本流程如图2所示：

图2 PSO-BP算法流程图

3 工程实例

场馆大跨钢结构的挠度变形受结构、应力、荷载、温度及风速等多种因素共同影响，需要根据实际情况进行变形因子的甄别和选取。下面以重庆市某国际会展中心北区主跨钢结构挠度监测为例，分析粒子群神经网络在大跨钢结构挠度监测中的应用。

经分析得知时效和温度是影响该场馆结构挠度的两个主要因素，因此将监测点的时效和温度数据作为输入、挠度变化量作为输出，通过粒子群神经网络学习训练，模拟出时效、温度与挠度变形量之间的关系模型，进而在已知时间间隔和温度的情况下，就可对结构的挠度变形趋势进行预测。

选取该结构6号挠度监测点(TPS06)的数据进行分析，将2014年5月23日的监测数据作为基准值；2014年6月3日～2015年11月4日共18期观测数据作为训练样本；2015年12月2日～2016年3月3日的4期数据作为预测样本，分别采用传统BP神经网络以及PSO-BP神经网络进行分析，以比较两种模型在算法效率以及预测精度方面的优劣。

首先需要确定网络的拓扑结构和参数，经过多次试验，确定了如表1所示的网络参数。

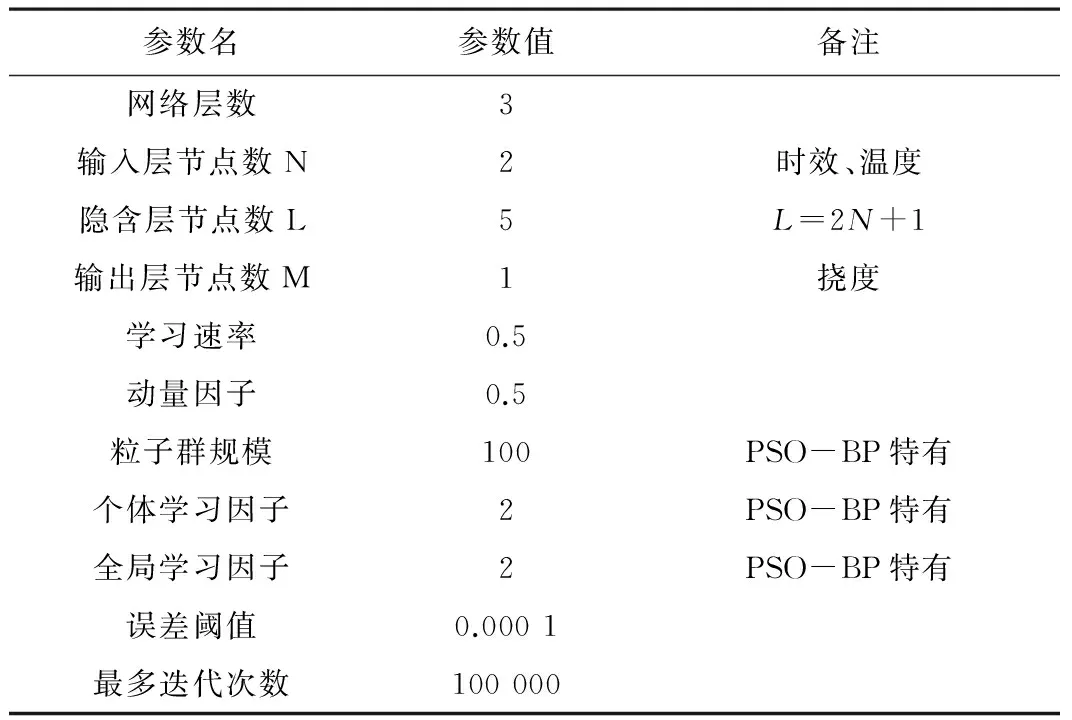
神经网络模型参数 表1

首先采用PSO-BP神经网络进行训练和预测，为了减小由于网络震荡及偶然因素的影响，分别进行20次训练和泛化，然后取泛化输出的平均值作为预测结果。训练数据以及训练输出如表2所示：

预测数据以及挠度预测值如表3所示：

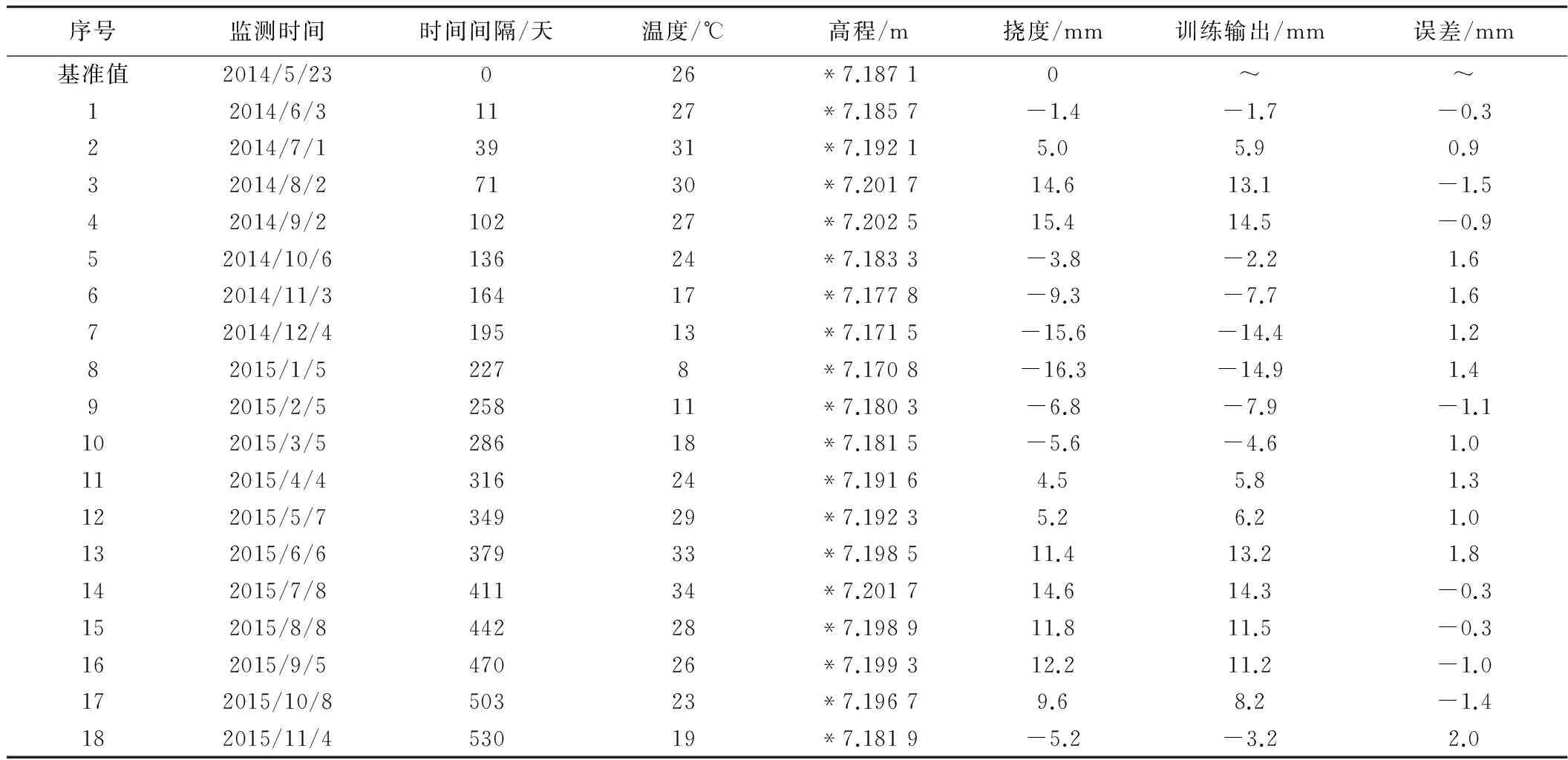
TPS06点训练样本及训练输出 表2

注：本文规定挠度变化值沿竖直方向上拱为正，下扰为负，高程数据前两位用*代替。

TPS06点预测样本及预测输出 表3

采用传统BP神经网络对TPS06点数据进行分析预测，将两种模型的预测结果从精度和效率方面进行对比和评价，结果如表4所示。

两种模型的挠度预测结果与实测值的对比如图2所示，20次训练及预测的平均误差如图3所示。

两种模型预测结果对照表 表4

图3 挠度实测值与模型输出值对比图

图4 历次训练及预测平均误差对比图

由表4可知，传统BP神经网络20次训练的收敛成功率为65%，平均迭代次数多，收敛速度慢，且训练输出和预测结果与实测值的误差较大；而粒子群神经网络历次训练均成功收敛，平均迭代次数远小于传统BP神经网络，同时训练和预测精度较高，最大误差的绝对值不超过 2 mm。图3以及图4也进一步表明了粒子群神经网络模型的训练及预测精度均高于传统BP模型。

4 结 论

工程实例表明，本文构建的粒子群神经网络与传统BP神经网络相比，在运算效率以及预测精度方面均有明显的提高，能够在对样本数据进行充分学习的基础上进行较为准确的预测。在实际应用中，可采用粒子群神经网络模型对已有监测数据进行训练，然后预测日期对应的时效和温度数据输入训练成熟的神经网络即可得到结构挠度变形预测值。

同时，为了使预测结果更加合理和精确，需要全面考虑导致大跨钢结构发生挠度变形的影响因素，如荷载、应力以及风速等，对这些因素进行监测并将数据用于神经网络模型的学习和训练，将有助于模型更加全面准确的获取变形趋势和规律，提高分析预测的精度和可靠性。

[1] 熊仲明，韦俊，曹欣等. 46.5m大跨度弧形钢拱结构的稳定及其缺陷影响分析[J]. 工程力学，2009，26(11)：172～178.

[2] 尹光志，李铭辉，李文璞等. 基于改进BP神经网络的煤体瓦斯渗透率预测模型[J]. 煤炭学报，2013：38(7)：1179～1183.

[3] 吴乃龙，周永领. 基于BP神经网络改进算法在地铁隧道施工中的沉降预测[J]. 城市勘测，2015，6(3)：148～150.

[4] 曹诗荣. 桥梁变形观测中GPS数据处理方法的研究[J]. 测绘通报，2011(5)：65～66.

[5] 邓跃进，王葆元，张正禄. 边坡变形分析与预报的模糊人工神经网络方法[J]. 武汉测绘科技大学学报，1998，23(1)：28～33.

[6] 戚丹，包腾飞，康业渊等. 基于逐步回归-BP神经网络的大坝变形监测模型[J]. 水电能源科学，2013，31(8)：109～111.

[7] 李波，柳华桥，戴鑫等. 标准BP神经网络算法和附加动量法在沉降监测中的应用研究[J]. 城市勘测，2016，2(1)：145～148.

[8] 周晓菲，杨艳梅. BFGS-BP法在变形监测数据处理中的应用[J]. 测绘科学，2012，37(3)：108～109.

[9] 韩立群. 人工神经网络教程[M]. 北京：北京邮电大学出版社，2006：5～14.

[10] 仲兆平，严青，邓学群等. 采用非线性粒子群算法的同步糖化发酵参数辨识[J]. 西安交通大学学报，2013，47(7)：1～6.

[11] 吴飞宇. 基于灰色神经网络模型的基坑变形预测研究[J]. 测绘通报，2013(S)：189～191.

[12] James Kennedy，Russell Eberhart.Particle swarm optimization[A]. In：Proceedings of the 4th IEEE International Conference on Neural Networks[C]. Piscataway：IEEE Service Center. 1995：1942～1948.

[13] 宋继光，秦勇，史健芳等. 粒子群算法及其在路由优化中的研究[J]. 计算机工程与设计，2010，31(9)：1905～1908.

Application of PSO-BP Neural Networks to Deflection Monitoring of Large-span Steel Structure

Xiao Xingguo1，Yuan Changzheng1，2，Li Chao1，2

(1.Chongqing Surveying Institute，Chongqing 401121，China；2.Chongqing Collaborative Innovation Center of Smart Sensing & Big Data，Chongqing 401121，China)

The traditional BP neural network model’s topological structure is difficult to determine，the rate of convergence is slow and its solution is likely to be a local optimal solution. In order to overcome these shortcomings，the PSO-BP neural network model was constructed by combining the PSO algorithm with the BP neural network，that is，using the PSO algorithm as the learning and training rules of BP neural network instead of the traditional one which based on the error function gradient descent guidelines. On this basis，the deflection monitoring data of a certain venues in Chongqing was taken as an example to verify the feasibility of the model in the deflection monitoring of large-span steel structure and its superiority on efficiency and accuracy compared with the traditional BP neural network.

BP neural network；PSO；large-span steel structure；deflection monitoring

1672-8262(2016)05-135-05

P258，TU196

A

2016—05—09

肖兴国(1976—)，男，高级工程师，主要从事工程测量相关工作。

住房和城乡建设部科学技术计划项目(2015-k8-012)