CGCS2000坐标系统转换引起宗地面积的变化

邱蕾，陈远鸿，杨志敏

(1.深圳市地籍测绘大队，广东 深圳 5180002； 2.深圳市勘察研究院有限公司，广东 深圳 5180261；3.武汉市测绘研究院，湖北 武汉 430079)



CGCS2000坐标系统转换引起宗地面积的变化

邱蕾1*，陈远鸿2，杨志敏3

(1.深圳市地籍测绘大队，广东 深圳 5180002； 2.深圳市勘察研究院有限公司，广东 深圳 5180261；3.武汉市测绘研究院，湖北 武汉 430079)

在我国，通常用宗地面积来确定权属范围内的面积，在实行CGCS2000国家大地坐标系后，各个地方的宗地面积需要从本地坐标系转换到CGCS2000国家大地坐标系下，本文结合实际地块面积，分析了由本地坐标系转换到CGCS2000国家大地坐标系引起的面积变化问题。

宗地面积；坐标转换；CGCS2000

1 引 言

在我国，城市独立坐标系普遍存在于各个城市，城市的基础地理信息数据基本也是以城市独立坐标系的成果进行保存，为了将城市的独立坐标系与国家的统一坐标系进行衔接，就需要进行坐标转换，这种坐标转换工作也是按需进行的。在深圳市的基础地理信息数据库中，各个宗地的基本属性，界址点坐标和面积都是以深圳独立坐标系存放的，为了将宗地的界址点坐标和面积上报，需要转换成CGCS2000国家大地坐标系的成果。将界址点的坐标进行转换后，宗地的面积也会发生一定的变化，因此研究和应用深圳独立坐标系转成CGCS2000国家大地坐标系的宗地面积变化对宗地面积的变形进行定量分析具有很强的指导意义。

2 宗地面积计算

深圳独立坐标系和CGCS2000国家大地坐标系的转换公式如式(1)和式(2)：

X′=X0+KXcosα-KYsinα

(1)

Y′=Y0+KXsinα+KYcosα

(2)

上两式中X′、Y′分别为某界址点在CGCS2000国家大地坐标系下的坐标，X、Y分别为界址点在深圳独立坐标系下的坐标，X0、Y0分别为深圳独立坐标系中的原点在CGCS2000国家大地坐标系下的坐标，α为旋转角，K为长度比。

由界址点坐标值计算各个宗地面积的公式如式(3)：

(3)

式(3)中当i=n时，i+1的值取1，i=1时，(i-1)的值取n。设(X′，Y′)表示在界址点在深圳独立坐标系中的坐标，(X，Y)表示界址点在CGCS2000国家大地坐标系的坐标。根据面积公式，可以得到在深圳独立坐标系中宗地的面积公式如式(4)，CGCS2000国家大地坐标系中的宗地面积计算公式如式(5)。

(4)

(5)

将式(1)和式(2)代入式(4)和式(5)中，即可得到如下：

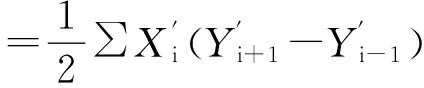
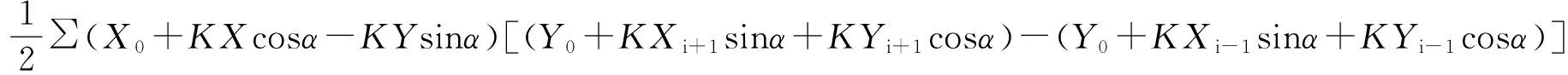
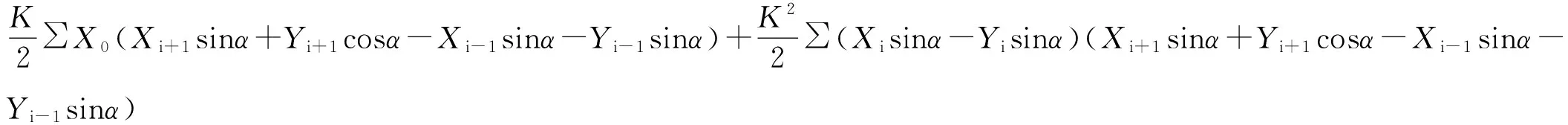
由上式可以得出：

SCGCS2000=K2S深圳

(6)

因此，深圳独立坐标系下计算出的宗地面积S深圳与CGCS2000坐标系下计算的宗地面积SCGCS2000成正比。但是在实际计算中，由于对转换CGCS2000坐标进行了四舍五入，因此实际转换后的CGCS2000坐标下的宗地面积与深圳独立坐标系下的宗地面积不仅仅存在固定比例关系，而且还包括四舍五入产生的偶然误差。

3 实例分析

在深圳实地选取了宗地数据，将所有宗地深圳独立坐标系下的面积和CGCS2000坐标系下的面积进行计算、统计，并且绘制了关系图如图1、图2和图3所示。

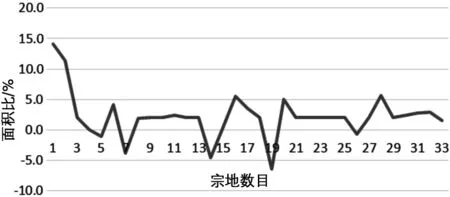
图1 面积差百分比

图1中横坐标为宗地个数，纵坐标的计算如(SCGCS2000-S深圳)/S深圳*100000。从图1中可以看出，坐标转换后的CGCS2000坐标下的宗地面积和深圳独立坐标系下的宗地面积之比并不是一个常数，这与上面推导的公式不一致。

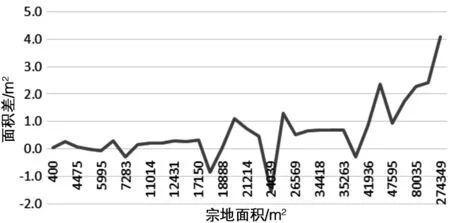
图2 面积差与面积大小关系图

图2中横坐标为宗地面积，纵坐标为转换后的面积与转换前的面积差。从图2中可以看出，面积差与宗地面积大小成正比。宗地面积越大，面积差越大。图3中横坐标为界址点个数，纵坐标为面积差。从图3中可以看出，面积差的大小与界址点个数无关。

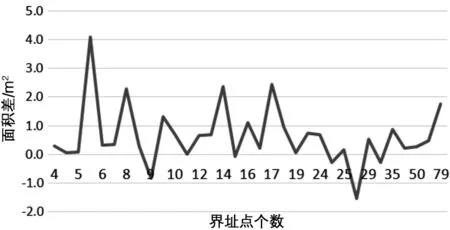
图3 面积差与界址点个数关系图

因此，深圳独立坐标系计算的宗地面积和CGCS2000转换后的宗地面积之差与宗地大小成正比，与宗地界址点个数及宗地形状没有关系。此外，本次检查的数据发现，转换前与转换后的宗地面积之差实际与宗地面积大小不是简单的正比关系，而是存在差值。分析其中主要原因是，转换前和转换后的宗地面积差包含两部分，一部分是系统差异，与宗地面积大小成正比。一部分是四舍五入引起的计算误差，通常是由于坐标末位四舍五入引起的误差导致的。计算误差的大小具有偶然性，与宗地面积大小和界址点数影响不显著。计算误差虽然影响不显著，但此项误差是可以避免的，只要不用经坐标末位四舍五入后的坐标来计算即可。为了验证这个结论，选取了12块宗地，将转换后的界址点的坐标保留小数后8位，根据(SCGCS2000-S深圳)/S深圳*100000计算比值，如图4所示。横坐标为宗地序号，纵坐标为比值。从图4中可以看出，保留了8位小数位的界址点坐标计算出来的面积与转换前的面积基本成正比，基本为一个常数。

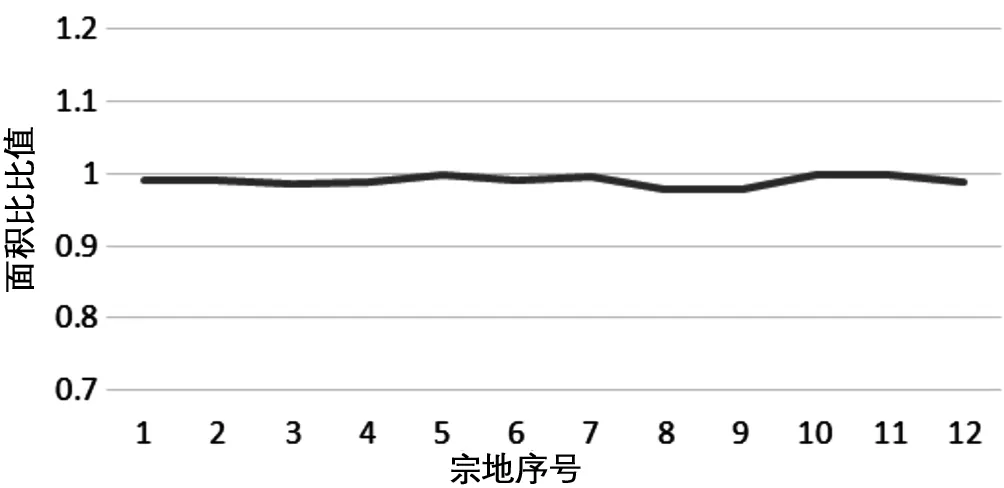
图4 面积比比值

4 结 论

自从国家推行CGCS2000国家大地坐标系后，从城市本地坐标系转换到CGCS2000国家大地坐标系已经成为国土部门的一个常态业务，其中宗地面积也是国土部门比较关心的一个指标，因此本文从理论和实践上对坐标转换前后的宗地面积进行了分析比较，对实际工作中宗地坐标转换的具有指导意义。从本文中的实验可以得到以下结论：经坐标转换后的宗地面积与原面积在数值上存在一定差值，宗地面积越大，面积差越大，与宗地界址点个数及宗地形状没有关系。

[1] 程鹏飞，成英燕，文汉江等. 2000国家大地坐标系实用宝典[M]. 北京：测绘出版社，2008.

[2] 李东，毛之琳. 基于CGCS2000的地方坐标系统建立方法的研究[J]. 测绘技术装备，2009，11(4)：3～5.

[3] 杨元喜. 2000国家大地坐标系[J]. 科学通报，2009(16)：2271～2276.

[4] 李茂奎，李新伟，赵勤军. 基于IGS参考站的GCGCS2000坐标系控制测量探讨[J]. 全球定位系统，2014(3)：93～96.

[5] 魏保峰，李国柱，倪曙等. 2000国家大地坐标与城市平面坐标转换方法的研究[J]. 测绘通报，2016(1)：57～61.

[6] 冯里涛，邓云青. 基于二维七参数模型的坐标转换参数的计算[J]. 城市勘测，2014(5)：108～110.

[7] 刘晖，时晓燕，杨沾吉等. 深圳市连续运行卫星定位服务系统的建立与试验[J]. 测绘通报，2003(9)：33～36.

[8] 罗和平，石晓燕，张天纪等. 深圳市连续运行卫星定位服务系统应用及其实时数据通讯技术分析[J]. 测绘与空间地理信息，2007，30(4)：36～39.

Change of the Cadastral Parcel Area Caused by CGCS2000 Coordinate System Conversion

Qiu Lei1，Chen Yuanhong2，Yang Zhimin3

(1.Shenzhen Cadastral Surveying and Mapping Office，Shenzhen 518034，China；2.Shenzhen Investigation & Research Institute Co.，Ltd.，Shenzhen 518026，China；3.Wuhan Geomatic Institute，Wuhan 430079，China)

In China，cadastral parcel area is used to determine the ownership of range area. In our country，each of the local land area requires a conversion from the local coordinates to the CGCS2000 coordinate with the implementation of the CGCS2000 national geodetic coordinate system. In this paper，the problems of the cadastral parcel area are analyzed when the coordinate system are converted.

cadastral parcel area；coordinate transformation；CGCS2000

1672-8262(2016)05-123-03

P258

B

2016—04—14

邱蕾(1981—)，女，高级工程师，主要从事大地测量相关工作。

国家自然科学基金(41504023)