天津市陆海坐标系统一转换研究

张奇，王文旭，张志全，王文江

(天津市测绘院，天津 西青 300381)



天津市陆海坐标系统一转换研究

张奇*，王文旭，张志全，王文江

(天津市测绘院，天津 西青 300381)

依托国家首批测绘地理信息公益性行业科研专项《天津市陆海一体化地理信息服务平台建设研究》，收集了天津市陆域、海域各坐标系及陆域、海域控制网资料，选取了坐标转换模型和坐标重合点，进行了坐标转换参数计算，确定了天津市陆、海坐标系统一转换关系并评定了转换精度，选取了检测点对坐标转换精度进行了检测，实现了天津市陆海坐标系的统一转换。

陆海一体化；平面基准；坐标转换；转换参数

1 研究背景

本研究依托国家首批测绘地理信息公益性行业科研专项《天津市陆海一体化地理信息服务平台建设研究》项目开展，目的是提供陆海地理空间信息平面基准转换与统一的理论和关键技术支持，通过对陆、海现用以及历史成果资料所用坐标系资料的搜集与调查、坐标系间转换关系的确定来实现陆、海多种平面坐标系之间的相互转换，为陆海地理信息数据融合提供支持[1]，目前国内尚无天津地区陆海坐标系统一转换的研究。

2 研究内容

天津市陆域现用坐标系为2000国家大地坐标系[2]以及1990年天津市任意直角坐标系，陆域历史成果用到1980西安坐标系；天津市海域现用的坐标系为2000国家大地坐标系，历史成果用到1980西安坐标系。由于陆域、海域现用的通用坐标系都是2000国家大地坐标系，因此本研究将重点放在涉及2000国家大地坐标系的坐标转换，包括2000国家大地坐标系与1980西安大地坐标系的转换，2000国家大地坐标系与1990年天津市任意直角坐标系的转换。本研究的主要内容包括收集天津市陆域、海域各坐标系资料及控制网资料，选取坐标转换模型和坐标重合点进行坐标转换参数计算，确定各坐标系之间的坐标转换关系，评定坐标转换精度，选取检测点对坐标转换精度进行检测[3]。

3 天津市陆、海坐标系统一转换

3.1 陆、海控制网

天津陆、海控制网统计如表1所示，分布如图1所示，陆域共有各等级控制点248个，海域共有各等级控制点34个。

陆、海平面控制点统计 表1

3.2 转换模型

常用的坐标转换模型包括Bursa七参数转换模型[4]以及二维高斯平面坐标转换模型[5]。本研究选用理论上更加严密的Bursa七参数转换模型进行陆海坐标系统一转换。

(1)

其中，三个平移参数[dxdydz]T，三个旋转参数[ωXωYωZ]T和一个尺度参数m。

图1 Bursa七参数转换示意图

3.3 重合点及检测点选取

重合点选取的原则是尽量选取数量足够的高等级、高精度且分布均匀的点作为坐标转换参数计算的重合点。在2000国家大地坐标系与1990年天津市任意直角坐标系的转换中，经过试算，均匀选取了48个重合点进行坐标转换参数的计算。在2000国家大地坐标系与1980西安坐标系转换参数计算中，除选取前述的48个陆域重合点外，还选取了19个海域坐标重合点，包括北方海区GPS控制网B级点6个以及C级点13个。

坐标转换参数计算完成、坐标转换关系确定后，须对坐标转换精度进行检测，本研究在天津陆、海域一共选取均匀分布的65个重合点进行坐标转换精度验证。

图2 坐标转换重合点及检测点分布

检测点分布如图2右中绿色圆点所示，65个检验点包括陆域50个(37个GPS C级点和13个连续运行基准站点)重合点，海域15个重合点(天津港附近GPS D级网控制点)。

3.4 转换参数计算

虽然陆域、海域控制点都有2000国家大地坐标系及1980西安坐标系成果，但因陆域、海域控制网施测时间不同，且未经过联合平差，其成果之间由于地表位移以及平差基准不完全相同而可能存在偏差。因此，必须联合陆域、海域控制点进行坐标转换参数计算。

利用前述重合点和坐标转换模型，采用最小二乘法[6]计算出2000国家大地坐标系与1980西安坐标系、1990年天津市任意直角坐标系之间的转换参数。具体计算过程如下，首先，将重合点坐标换算为空间直角坐标；其次，使用全部的重合点求取转换参数，再利用该转换参数回代，求得已知点的坐标，计算已知点的残差；再次，分析残差值大于 0.1 m点的可靠性，检查点位和成果的正确性，重新确定重合点；最后，重复上述步骤，直到回代残差到一定范围内为止。计算得到各重合点转换残差(平面)如图3所示。从图3可以看出，2000国家大地坐标系到1980西安坐标系转换中，在天津市东部沿海以及西部市界处，陆域重合点残差较大，个别点如唐家河以及西北斜残差(平面)达到了 0.3 m。2000国家大地坐标系到1990年天津市任意直角坐标系转换中，重合点转换残差(平面)小于 0.11 m，在武清西部、汉沽、大港重合点坐标转换残差较大。

表2统计了重合点转换残差绝对值在x方向、y方向、平面上的最小值、最大值、平均值以及中误差。从表中可以看出，2000国家大地坐标系到1980年西安坐标系转换中，重合点坐标转换残差在x方向上为 0.104 m，y方向为 0.102 m，平面上为 0.146 m。2000国家大地坐标系到1990年天津市任意直角坐标系转换中，重合点坐标转换残差在x方向上为 0.042 m，y方向为 0.043 m，平面上为 0.060 m。

图3 坐标系转换残差 重合点残差绝对值统计表 表2

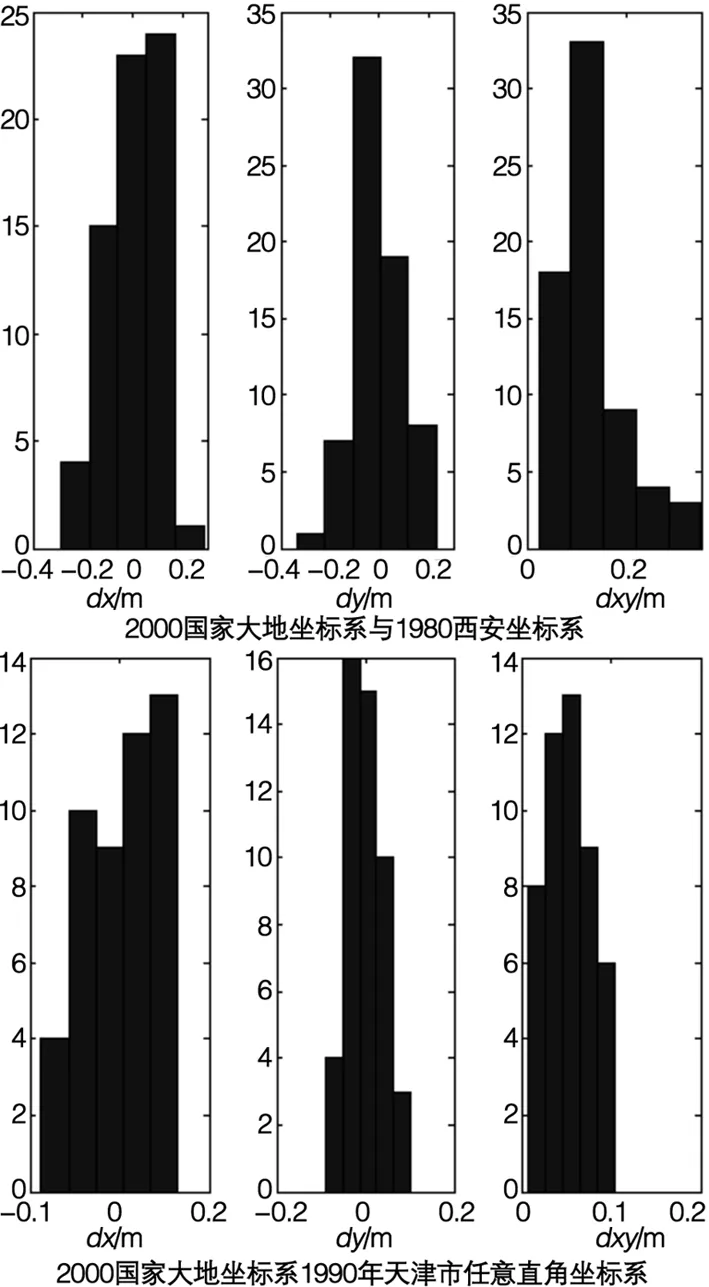
图4 重合点2000国家大地坐标系与1980西安坐标系转换残差分布

各重合点残差分布如图4所示。从图4可以看出，2000国家大地坐标系到1980年西安坐标系转换中重合点残差x方向和y方向绝大多数在 ±0.1 m之间。2000国家大地坐标系到1990年天津市任意直角坐标系转换中重合点残差x方向上在 ±5 cm以内，在y方向残差在在 ±0.11 m之内，在平面上小于 0.11 m。

参与2000国家大地坐标系与1980西安坐标系间转换参数计算的国家一、二等三角点大多数于上世纪50年代～70年代布设施测，由于我国地壳运动变化复杂，经过多年，这些三角点点位发生了不同程度的变化。为了使坐标转换结果和1980西安坐标系下的历史成果进一步符合以达到项目设计书中坐标转换精度优于 10 cm的要求，同时兼顾不对坐标系的均匀性产生过大的影响，本研究依据最小二乘原理，采用二次多项式对2000国家大地坐标系到1980西安坐标系转换参数计算中的重合点的残差进行了拟合，采用拟合得到的二次曲面进行残差分配，图5为x方向和y方向的残差拟合曲面。

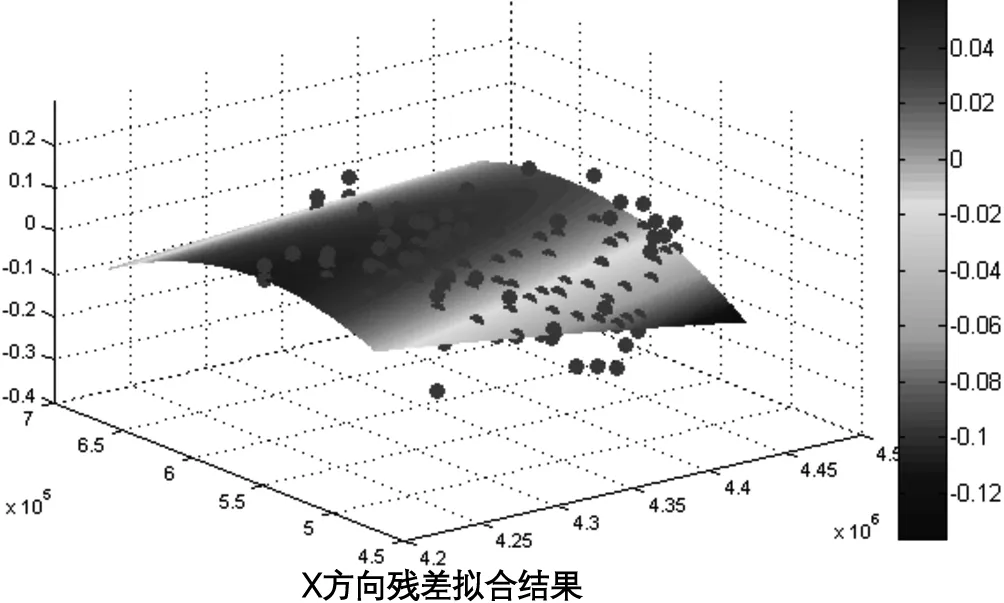
图5 2000国家大地坐标系到1980年西安坐标系转换残差拟合

采用二次曲面进行残差分配后，得到2000国家大地坐标系到1980年西安坐标系转换残差中误差在x方向和y方向上分别为 0.076 cm和 0.073 cm，大大优于不进行残差拟合的结果。

3.5 精度推算

坐标转换关系确定后，需要对坐标转换精度进行推算[7]。

(1)V(残差)=重合点已知坐标-重合点转换坐标

(2)残差中误差

坐标转换精度是通过求取转换参数的重合点的残差中误差体现的。2000国家大地坐标系坐标与1980西安坐标、1990年天津市任意直角坐标系坐标转换精度统计如表3所示。

坐标转换残差中误差统计表 表3

从表3可以看出，2000国家大地坐标系与1980西安坐标系转换精度较差，x方向和y方向上分别为 0.071 4m和 0.068 8m，2000国家大地坐标系到1990年天津市任意直角坐标系坐标转换的精度在x方向和y方向分别为 0.041 6m和 0.042 6m，优于2000国家大地坐标系与1980西安坐标系转换精度，原因是参与其转换参数计算的重合点于2005年进行过复测，成果现势性较好。

3.6 外符合精度评估

确定坐标转换关系后，进行了坐标转换精度检测。以检测点通过坐标转换得到的坐标与其原始坐标的较差来检测坐标转换精度。精度检测点转换后坐标与原始坐标较差分布如图6所示，统计表如表4所示。

图6 精度检测点转换经转换得到坐标与原始坐标较差分布

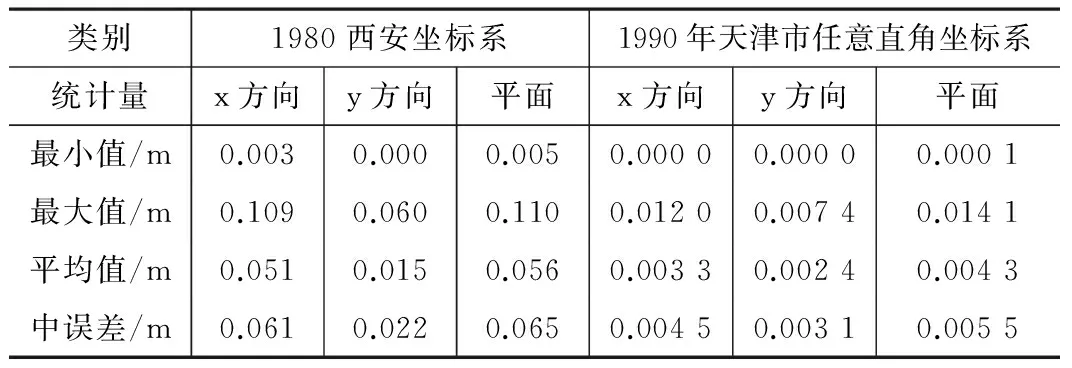
检测点偏差统计表 表4

由表4及图6可以看出，在2000国家大地坐标系到1980年西安坐标系转换中，检测点偏差在x方向、y方向、平面中误差分别为 0.061m、 0.022m、和 0.065m，在2000国家大地坐标系到1990年天津市任意直角坐标系转换中，检测点偏差在x方向、y方向、平面中误差分别为 0.005m、 0.003m、和 0.005m。

联合坐标转换重合点残差与精度检测点偏差[8]，可以得到2000国家大地坐标系与1980西安坐标系、1990年天津市任意直角坐标系之间转换精度空间分布如图7所示。

从转换精度分布图中可以看出，2000国家大地坐标系到1980西安坐标系转换精度在天津西部市界(武清西部)以及天津东南沿海(包括汉沽东部、塘沽、大港)低于市内其他区域，在天津南部近海区域转换精度低于东部近海。2000国家大地坐标系到1990年天津市任意直角坐标系转换精度在市界处(蓟县东部、宁河东部、汉沽东部、大港西南部、武清西南部与静海西北部等区域)低于市内区域。

4 结 论

本文收集了天津市陆、海各坐标系资料及陆、海控制网资料，选取了坐标转换模型和坐标重合点，进行了坐标转换参数计算，确定了各坐标系之间的坐标转换关系，评定了坐标转换精度，并选取检测点对坐标转换进行了精度检测。研究结果表明，采用本文所确定的坐标转换关系进行2000国家大地坐标系到1980年西安坐标坐标系的转换，x方向和y方向中误差分别为 0.071 4m和 0.068 8m，2000国家大地坐标系到坐标1990年天津市任意直角坐标系坐标转换，x方向和y方向中误差分别为 0.041 6m和 0.042 6m。

坐标转换除本文所研究的正向转换外，还包括逆向转换，即1980西安坐标系、1990年天津市任意直角坐标系到2000国家大地坐标系的转换。反向转换与正向转换采用的转换模型相同，重合点相同，转换精度及其分布特性理论上也相同，本文不予赘述。

[1] 殷晓冬，胡家升，张立华等. 海岸带多源数据三维无缝拼接技术[J].大连海事大学学报，2008(2)：19～23.

[2] 杨华忠，李军，汪舟平等. 我国常用大地坐标系与2000 中国大地坐标系间的转换[J]. 中国测绘学会大地测量专业委员会2007年综合性学术年会，2007(11)：1～10.

[3] 焦立芬. 基于坐标转换重合点的分布、密度、精度与转换精度分析[J]. 测绘技术装备，2013(4)：25～28.

[4] 陈宇，白征东，罗滕. 基于改进的布尔沙模型的坐标转换方法[J]. 大地测量与地球动力学，2010(03)：71～73.

[5] 陈义，沈云中，刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报信息科学版，2004(12)：1101～1105.

[6] 邱卫宁，陶本藻，姚宜斌. 测量数据处理理论与方法[M]. 武汉：武汉大学出版社，2008.

[7] 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉：武汉大学出版社，2003.

[8] 钟业勋，童新华，王龙波. 从1980西安坐标系到2000国家大地坐标系的坐标变换[J]. 海洋测绘，2010(30)：1～3.

Study on the Transformation of Coordinate System Integrating Land and Sea in Tianjin

Zhang Qi，Wang Wenxu，Zhang Zhiquan，Wang Wenjiang

(Tianjin Institute of Surveying and Mapping，Tianjin 300381，China)

This study is supported by the first batch of the national public sector special research of surveying and mapping geographic information "The study on the construction of the platform of geographic information service integrating sea and land in Tianjin”. In this paper，firstly the information of the coordinate system and the control network of sea and land of Tianjin are collected，then the coordinate transformation model and coordinate coincidence points are selected，thirdly the coordinate transformation parameters are calculated and the transformation relationship of coordinate system of Tianjin land and sea is determined，then the accuracy of the transformation is evaluated and detected，finally the unity of Tianjin land and sea coordinate system transformation has been realized.

integration of land and sea；datum of plane；coordinate transformation；transformation parameters

1672-8262(2016)05-91-05

P226.3

A

2016—04—18

张奇(1988—)，男，硕士，工程师，主要从事天津市地理信息空间基准维护方面的工作。

国家测绘地理信息局2014年测绘地理信息公益性科研专项(201412012)