基于强震动记录确定的场地卓越周期

陈永新 迟明杰 李小军

1) 中国北京100081中国地震局地球物理研究所 2) 中国太原030021山西省地震局 3) 中国北京100081中国地震局地震观测与地球物理成像重点实验室



基于强震动记录确定的场地卓越周期

1) 中国北京100081中国地震局地球物理研究所 2) 中国太原030021山西省地震局 3) 中国北京100081中国地震局地震观测与地球物理成像重点实验室

本文介绍了3种根据场地强震动记录获取场地卓越周期的方法： ① 地表记录的傅里叶谱分析法； ② 地表水平/垂直傅里叶谱比法； ③ 地表/地下傅里叶谱比法. 基于日本强震动观测台网KiK-net中两个基岩台站和两个Ⅲ类场地台站获取的数百条强震动记录， 分别使用上述3种方法确定场地的卓越周期， 并对比分析各种方法的优缺点及其适用情况. 结果表明： 对于基岩场地， 由于记录信息复杂， 局部场地条件对地震动影响较小， 地震动自身特性突出， 导致3种方法所得到的结果均比较分散； 对于土层场地， 场地条件影响比较显著， 3种方法基本都可以得到一个较为准确的数值； 但对于某些场地， 地表水平/垂直傅里叶谱比法所得结果存在不确定性， 相比之下， 地表/地下傅里叶谱比法则能给出一个更为准确的场地卓越周期值.

强震动 场地条件 傅里叶谱比 卓越周期

引言

场地卓越周期是描述场地特性的重要指标． 地表土层对不同周期的地震波有选择放大作用， 致使在地震记录图上显示某些周期的波形特别多且好， 即显得“卓越”， 故称为地震卓越周期(《岩土工程手册》编写委员会， 1994)． 确定场地卓越周期的方法有以下3种(童广才， 刘康和， 2000): ① 当场地内有强震动记录时， 通过频谱分析确定； ② 由常时微动测试分析确定； ③ 根据场地分层剪切波速测试结果按其子层周期求和公式计算． 前两种方法均是通过确定场地的地震动卓越周期以进一步确定场地的卓越周期． 高广运等(2000)和陈鹏等(2009)将卓越周期分为记录卓越周期Tr、 测试卓越周期Tm和波速卓越周期Tv．Tr为真实反应地震动的卓越周期(利用地震动卓越周期间接反映场地卓越周期， 该周期也在不同程度上受到地震震源谱特性和区域地壳介质对地震波传播的影响)， 当工程场地范围内有适宜的强震动记录时， 抗震设计应首选Tr;Tm为接近场地固有周期的卓越周期;Tv为与场地固有周期相比有一定误差的卓越周期， 除非地基土层基本满足均匀平行的条件， 否则应尽量避免选用．

场地卓越周期在数值上与卓越频率互为倒数， 因此卓越周期可由卓越频率求倒得出． 目前日本强震动观测台网KiK-net记录中既有场地地下记录(NS1， EW1， UD1)， 也有地表记录(NS2， EW2， UD2)， 因此对场地内强震记录通过频谱分析确定其卓越频率时可以采用以下3种方法： ① 地表记录的傅里叶谱分析法； ② 地表水平/垂直傅里叶谱比法(Wenetal， 2006； 任叶飞等， 2013)； ③ 地表/地下傅里叶谱比法．

本文拟选取日本强震动观测台网中两个基岩台站和两个Ⅲ类场地台站的数百条记录， 分别采用上述3种方法对两个基岩台站和两个Ⅲ类场地台站的卓越频率进行分析， 并对比分析各种方法的优缺点及其适用情况．

1 强震动数据

本文从日本强震动观测台网中选取了FKOH06和KGSH03两个基岩台站以及TCGH16和IBRH17两个Ⅲ类场地台站， 这些台站分别有地表和相应的地下观测点， 各台站分别获得了大量的地震事件记录． 在选择台站地震动记录时， 对地震事件随机选取， 但是需注意所选的地震动记录峰值加速度的分布应尽量能覆盖各个等级． 最终用于本文研究的强震动记录为： FKOH06台站29次地震事件的地表和地下记录， 共174条； KGSH03台站25次地震事件的地表和地下条记录， 共150条； TCGH16台站45次地震事件的地表和地下记录， 共270条； IBRH17台站33次地震事件的地表和地下记录， 共198条．

2 数据分析

首先使用ViewWave软件读取地震记录， 该软件默认对记录进行滤波和基线校正； 其次进行傅里叶变换， 分别绘制出各条记录的傅里叶谱以及地表/地下和地表水平分量/垂直分量的傅里叶谱比曲线， 读取傅里叶谱最大幅值以及傅里叶谱比曲线中谱比最大值所对应的频率值， 即为卓越频率； 然后分别绘制出各场地经上述3种方法分析得到的卓越频率的散点分布图； 最后对比卓越频率的分布情况， 分析在确定场地卓越频率时各方法的适用性．

图1—6给出了FKOH06和KGSH03两个基岩台站所在场地的卓越频率分布． 由图1和图4可以看出， 基岩台站地下和地表记录的3个分量的傅里叶谱卓越频率分布均很分散． 由图2和图5可以看出， 台站所在场地的地表水平/垂直傅里叶谱比卓越频率分布也都很分散． 由图3和图6可以看出， 场地的水平分量和垂直分量的地表/地下傅里叶谱比卓越频率分布不同： 对于FKOH06台站所在场地， 水平分量南北向和东西向卓越频率分布比较分散， 而垂直分量卓越频率分布相对集中； 对于KGSH03台站所在场地则得到相反的结论． 综上， 对于基岩场地卓越频率， 上述3种方法所得结果均很分散， 无法给出一个准确的卓越频率值， 这表明基岩地震动的卓越周期主要反映的是地震震源谱特性和区域地壳介质对地震波传播的影响， 而局部基岩场地对地震动卓越周期的影响则不明显．

图1 基岩台站FKOH06所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布图中数字1和2分别表示地下和地表， 下同

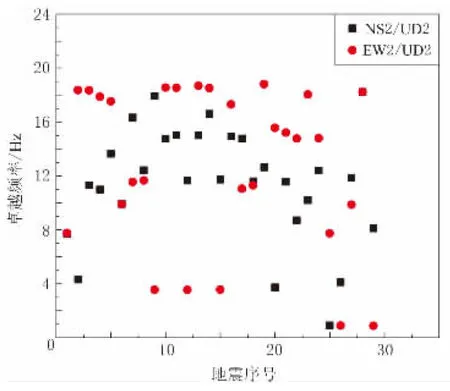
图2 基岩台站FKOH06的地表水平/垂直傅里叶谱比卓越频率分布

图3 基岩台站FKOH06的地表/地下傅里叶谱比卓越频率分布

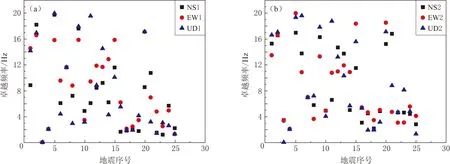
图4 基岩台站KGSH03所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布

图5 基岩台站KGSH03的地表水平/垂直傅里叶谱比卓越频率分布

图6 基岩台站KGSH03的地表/地下傅里叶谱比卓越频率分布

图7—12为Ⅲ类场地台站的卓越频率分布图. 由图7和图10可以看出: Ⅲ类场地台站TCGH16和IBRH17地下记录的3个分量的傅里叶谱卓越频率分布比较分散； TCGH16台站地表水平分量的傅里叶谱卓越频率分布比较集中， 约为4.47 Hz, 而其垂直分量的傅里叶谱卓越频率分布比较分散； IBRH17台站地表水平分量和垂直分量的傅里叶谱卓越频率分布均比较集中， 分别约为8.96 Hz和 10.26 Hz． 由图8和图11可以看出， TCGH16台站所在场地的地表水平/垂直傅里叶谱比卓越频率分布比较集中， 约为4.53 Hz， 而IBRH17台站所在场地则比较分散． 由图9和图12可以看出， TCGH16和IBRH17台站所在场地的地表/地下傅里叶谱比卓越频率分布均比较集中， 其所在场地的水平分量的地表/地下傅里叶谱比卓越频率分别约为4.54 Hz和9.35 Hz， 相应垂直分量约为11.29 Hz和11.39 Hz． 由上述结果可知： 对于TCGH16台站所在场地， 3种方法均能给出一个相对确定的卓越频率值， 分别为4.47 Hz， 4.53 Hz和4.54 Hz； 对于IBRH17台站所在场地， 地表水平/垂直傅里叶谱比卓越频率分布比较分散， 而由地表记录傅里叶变换所得到的卓越频率为8.96 Hz， 由地表/地下傅里叶谱比法得到的卓越频率为9.35 Hz．

图7 TCGH16台站所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布

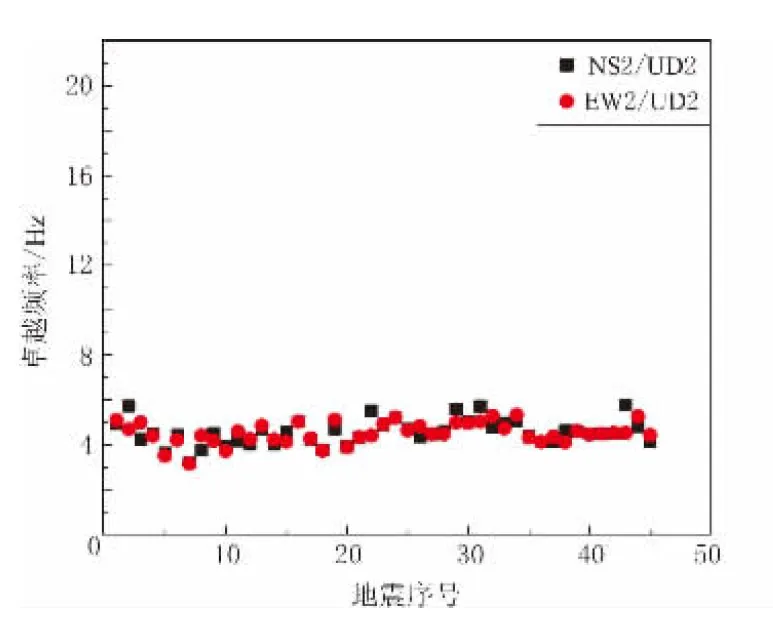
图8 TCGH16台站的地表水平/垂直傅里叶谱比卓越频率分布

图9 TCGH16台站的地表/地下傅里叶谱比卓越频率分布

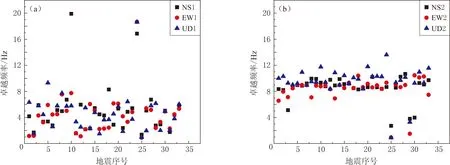
图10 IBRH17台站所在场地的地下(a)和地表(b)傅里叶谱卓越频率分布

Fig.10 The distribution of Fourier spectrum dominant frequency in the site of station IBRH17 on the underground (a) and surface (b)

图11 IBRH17台站的地表水平/垂直傅里叶谱比卓越频率分布

Fig.11 The distribution of surface horizontal/vertical Fourier spectral ratio dominant frequency in station IBRH17

图12 IBRH17台站的地表/地下傅里叶谱比卓越频率分布

Fig.12 The distribution of surface/underground Fourier spectral ratio dominant frequency in station IBRH17

3 讨论与结论

对于基岩台站FKOH06和KGSH03所在场地， 由3种方法所得的卓越频率分布均比较分散， 无法给出一个确定的数值， 初步认为是由于场地岩层坚硬、 局部场地条件对地震动影响较小所致， 因此场地地表和地下记录所体现的主要还是地震震源谱特性和区域地壳介质对地震波传播的影响， 而场地上不同地震的震源及地震波传播路径存在较大差异， 从而导致所得的场地卓越频率分布比较分散．

对于Ⅲ类场地， TCGH16和IBRH17台站所在场地的土层条件不同， 上述3种方法在具体场地的适用性也不同． 对于TCGH16台站所在场地， 3种方法均能给出一个确定的卓越频率数值， 且3种方法所得数值很接近． 对于IBRH17台站的所在场地， 地表水平/垂直傅里叶谱比卓越频率分布比较分散， 无法给出确定数值， 而另外两种方法均可给出确定数值， 但数值相差较大． 结合两个台站所在场地的具体土层条件分析， TCGH16和IBRH17台站所在场地土层均为砂层、 砂砾夹有黏土层， 但等效剪切波速(前者172 m/s左右， 后者272 m/s)及覆盖土层厚度(前者约75 m， 而后者深达235 m)差别较大， 初步认为是地表土层剪切波速及土层厚度的影响所导致的．

综合上述3种方法的分析结果， 可以得到如下结论：

1) 地表记录傅里叶谱分析法所得的卓越频率所包含信息较多， 既有地震震源和区域地壳介质的影响， 也有局部场地特性影响． 对于基岩场地， 由于场地条件对地震动影响较小， 而地震震源和区域地壳介质的影响比较突出， 因此同一场地上由不同记录得出的结果偏差较大， 如上述两个基岩台站所在场地． 但对于地表有土层的场地， 场地条件对地震动影响明显， 可以得出较为准确的结果．

2) 地表水平/垂直傅里叶谱比法的前提是认为场地条件对地震动垂直分量的影响相对于水平分量要小得多， 但当场地地表为较厚土层时， 场地条件对地震动垂直分量的影响也较大， 因此该方法在某些场地适用(如TCGH16台站所在场地)， 但在某些场地所得结果却很分散(如IBRH17台站所在场地)．

3) 地表/地下傅里叶谱比法理论上最能反映场地条件对地震动的影响， 本文认为该方法所得场地卓越频率是比较准确的． 作者还选取了20次不同地震事件在TCGH16台站的地震动记录与相邻的TCGH12台站的地震动记录进行了对比分析， 结果显示两个台站地下记录的傅里叶谱差异很小(图13)， 但在地表差异却较大(图14)， 这说明地表/地下傅里叶谱比法确实能很好地体现场地条件对地震动的影响， 从而验证了该方法的准确性．

对于基岩场地， 由于局部场地条件的影响相对较弱， 地震动频谱中包含的场地特性影响信息很少， 所以3种方法所得结果均很分散； 对于地表存在土层的场地， 地表水平/垂直傅里叶谱比法所得结果存在不确定性， 而地表/地下傅里叶谱比法则能给出一个相对较为准确的场地卓越频率值．

图13 TCGH16(a)和TCGH12(b)台站地下记录的傅里叶谱

Fig.13 Fourier spectrum recorded by station TCGH16 (a) and TCGH12 (b) on the underground

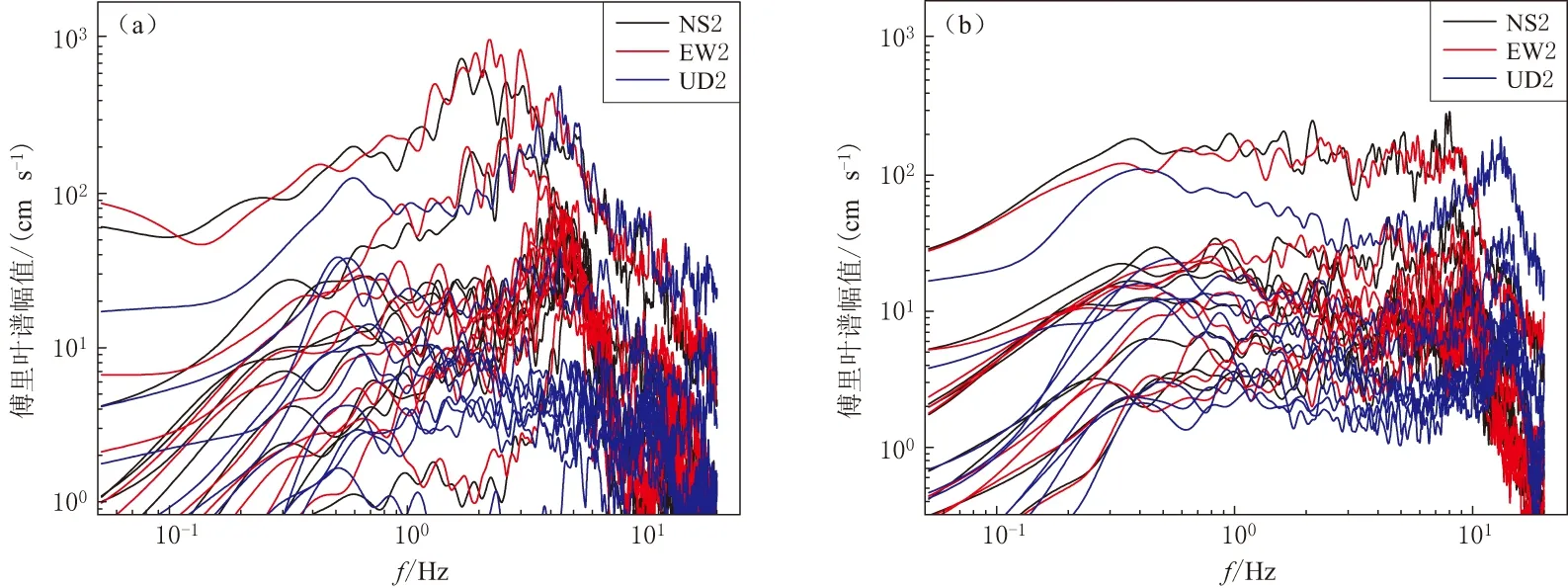
图14 TCGH16(a)和TCGH12(b)台站地表记录的傅里叶谱

Fig.14 Fourier spectrum recorded by station TCGH16 (a) and TCGH12 (b) on the surface

陈鹏， 刘文锋， 付兴潘. 2009. 关于场地卓越周期和特征周期的若干讨论[J]. 青岛理工大学学报， 30(6): 29--35.

Chen P， Liu W F， Fu X P. 2009. Discussions on site predominant period and characteristic period[J].JournalofQing-daoTechnologicalUniversity， 30(6): 29--35 (in Chinese).

高广运， 吴世明， 周健， 刘奋勇. 2000. 场地卓越周期的讨论与测定[J]. 工程勘察， (5): 29--31.

Gao G Y， Wu S M， Zhou J， Liu F Y. 2000. Discussion and measurement on site predominant period[J].GeotechnicalInvestigation&Surveying， (5): 29--31 (in Chinese).

任叶飞， 温瑞智， 山中浩明， 鹿嶋俊英. 2013. 运用广义反演法研究汶川地震场地效应[J]. 土木工程学报， 46(增刊2): 146--151.

Ren Y F， Wen R Z， Hiroaki Y， Toshihide K. 2013. Research on site effect of Wenchuan earthquake by using generalized inversion technique[J].ChinaCivilEngineeringJournal， 46(Suppl 2): 146--151 (in Chinese).

童广才， 刘康和. 2000. 场地卓越周期的确定[J]. 电力勘测， (2): 43--46.

Tong G C， Liu K H. 2000. Determine predominant period of site[J].ElectricPowerSurvey， (2): 43--46 (in Chinese).

《岩土工程手册》编写委员会. 1994. 岩土工程手册[M]. 北京: 中国建筑工业出版社: 769--770.

Editorial Board ofGeotechnicalEngineeringManual. 1994.GeotechnicalEngineeringManual[M]. Beijing: China Architecture & Building Press: 769--770 (in Chinese).

Wen K L， Chang T M， Lin C M， Chiang H J. 2006. Identification of nonlinear site response using theH/Vspectral ratio method[J].TerrAtmosOceanSci， 17(3): 533--546.

Determination of site dominant period based on strong motion records

1)InstituteofGeophysics，ChinaEarthquakeAdministration，Beijing100081，China2)EarthquakeAdministrationofShanxiProvince，Taiyuan030021，China3)SeismicObservationandGeophysicalImagingLaboratory，ChinaEarthquakeAdministration，Beijing100081，China

In this paper, we introduce three methods for determining dominant period based on the strong motion records, they are ① the Fourier spectral analysis method of surface records； ② horizontal/vertical Fourier spectral ratio method； ③ surface/underground Fourier spectral ratio method. Several hundred strong motion records from two bedrock stations and two stations on site class Ⅲ in the KiK-net strong motion observation network in Japan are used to analyze the site dominant period. It is concluded that， on the bedrock site， the dominant frequency obtained from the three methods are scattered due to the hard rock site condition which has little effect on the ground motion. On the soil site， the overlying soil has great effect on the ground motion， and accurate values of dominant period can be obtained from the three methods. The dominant frequency from the surface/underground Fourier spectral ratio method is more accurate than that from the surface horizontal/vertical Fourier spectral ratio method whose result is uncertain on some soil sites.

strong motion; site condition; Fourier spectral ratio; dominant period

国家国际科技合作项目(2012DFG20510)和环保公益性行业专项(201309056)共同资助.

2015-03-25收到初稿， 2015-06-04决定采用修改稿.

e-mail: chenyoyi@126.com

10.11939/jass.2016.01.014

P315.9

A

陈永新, 迟明杰, 李小军. 2016. 基于强震动记录确定的场地卓越周期. 地震学报, 38(1): 138--145. doi:10.11939/jass.2016.01.014.

Chen Y X, Chi M J, Li X J. 2016. Determination of site dominant period based on strong motion records.ActaSeismologicaSinica, 38(1): 138--145. doi:10.11939/jass.2016.01.014.