基于Contourlet的图像融合方法❋

王　建，王必宁，侯维刚

（1．西安航空学院计算机学院，西安710077；2．西安热工研究院有限公司，西安710032）

·微机软件·

基于Contourlet的图像融合方法❋

王建1，王必宁2，侯维刚1

（1．西安航空学院计算机学院，西安710077；2．西安热工研究院有限公司，西安710032）

针对两幅严格配准的同一场景左聚焦和右聚焦图像融合问题，设计了一种基于Contourlet变换的多聚焦图像融合方法。应用Contourlet变换对源图像进行多尺度、多方向分解，分别采用主成分分析法和区域结构相似度的融合规则得到融合图像的低通子带系数和带通方向子带系数，经过Contourlet逆变换得到融合图像。实验结果和定量分析结果表明，融合成为一幅清晰的单一聚焦图像，且将熵提高2．64%～3．15%，相关系数提高0．11%～0．57%，平均梯度提高4．44%～51．4%。

多聚焦图像；Contourlet变换；主成分分析；结构相似度；图像融合；融合规则

1　引　言

图像融合技术已经在计算机视觉、机器人、自动目标识别等方面进行了研究，其应用领域非常广阔。多聚焦图像的产生是由于光学成像系统聚焦范围的限制，在相同焦距下无法获得远近不同或距离不同的多个目标都清晰的图像，必须分别采取不同的焦距以获得各自清晰的多幅图像［1］。

图像融合的主要方法是基于金字塔变换和基于小波变换的方法［2－3］。由于，金字塔分解结构中不同层次的分辨率细节彼此相关，融合方法的稳定性差；小波变换虽然提高了金字塔融合方法的稳定性，但其只具有3个方向的分解，只能反映点奇异性，不能较好地表达图像中的线、面奇异性。因此，提出了多尺度几何分析方法Contourlet变换，该变换具有各向异性和多方向性的特点，与小波变换相比具有更好的稀疏表达能力，能更好地描述图像方向的奇异性特征［4－5］。

在以上方法的基础之上进行了深入研究，给出了一种基于Contourlet变换的多聚焦图像融合方法。首先对待融合图像进行Contourlet变换，分解成低通子带和带通方向子带；然后采用PCA的融合规则和区域结构相似度的融合规则来获取相应的系数；再对其进行Contourlet的反变换以得到最终融合图像；最后采用客观评价对融合方法的性能进行定量分析和比较。实验结果和定量分析比较的结果均说明该融合方法法具有较好的优越性。

2　Contourlet变换

M．N．Do和M．Vetterli于二十一以世纪初提出一种二维图像稀疏表达方法即Contourlet变换，该方法主要解决了小波变换无法识别数字图像中固有的线面奇异和方向性信息差的缺点，采用类似于轮廓段（Contour Segment）的光滑结构来逼近图像，其支撑区间是“长条形”结构且具备随尺度变化长宽比例［6－7］。Contourlet变换除了拥有小波变换的多尺度、时域和频域局部特性之外，还具有良好的多分辨率、局部化、各向异性和多方向特性，能够对光滑曲线采用比较少的系数来表达，以便更好地捕捉图像的边缘信息。

Contourlet变换利用双重滤波器组结构实现一种多尺度、多方向的图像表示方法。第一步，二维图像采用拉普拉斯金字塔（Laplacian Pyramid，LP）变换进行分解，产生一个下采样的原始图像一半的低通子带和一个与原始图像分辨率相同的高通子带。再次采用拉普拉斯金字塔变换对低通子带图像进行迭代分解，以便将原始图像分解为一系列不同尺度上的高通和低通子带图像。第二步，高通子带图像采用方向滤波器组（Directional Filter Bank，DFB）进行多方向分解，对拉普拉斯金字塔分解所得到的每层高通子带图像都进行多方向分解，以便将分布在同方向的奇异点合成一个系数。方向滤波器组包括两个模块：第一个模块是两通道的Quincunx梅花扇形滤波器组，用扇形滤波器将2－D光谱分解成垂直和水平两个主要方向。第二个模块是Shearing平移操作，其作用是旋转重采样并且宽度变为原来的两倍，以实现图像信息在其余方向的分析，捕获图像的线和面的奇异性。最终目标是将高通子带图像信息的频域划分成2的n次方个楔形区域［7］。Contourlet变换原理结构框图如图1所示。

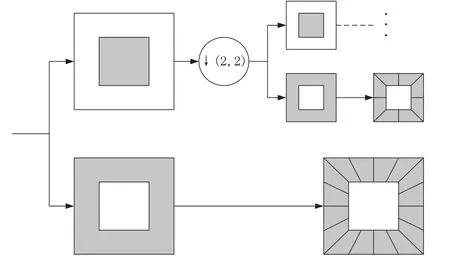
图1　Contourlet变换原理结构框图

Contourlet变换之后的系数分布由塔式方向滤波器组（Pyramidal Directional Filter Bank，PDFB）分解时所给定的参数numlevs决定。numlevs为一维向量，numlevs向量中的每一个值对应每一级塔式方向滤波器组分解级数的系数。在金字塔分解的过程中，如果方向滤波器组分解级数的系数为0，则必须严格采用二维小波分解来处理；如果分解级数的系数为K，则该层级上方向滤波器组分解的级数为2K个方向。Contourlet变换之后的系数coeffs与分解参数numlevs相对应，变换所得到的系数coeffs是一个多维向量组，向量组的长度Length是向量numlevs的长度加1。其中coeffs｛1｝是低通子带图像，coeffs｛i｝（i＝2，…，Length）代表金字塔第i层级上DFB分解所得到的方向子带图像。当numlevs为［0，3，4］时，待融合图像大小为512×512，待融合图像的3级Contourlet变换示意图如图2所示。由图2可知，Contourlet分解的最上层是低通子带系数，中间层和最下层都是带通方向子带系数，且中间层分解的级数为8个方向，最下层分解的级数为16个方向。

3　融合方法

在图像融合之前，待融合的多聚焦图像A和B已经过严格的空间配准。基于Contourlet变换的多聚焦图像融合步骤如下：

（1）对源图像A和B分别采用Contourlet变换进行J层（J＝3）分解，得到不同尺度和方向子带系数。其中，和为低通子带，和为带通方向子带，k＝1，2，．．．，2nj，j＝1，2，…J。J代表分解的最大层次，2nj代表每一层分解的方向数目。

（2）对源图像A和B的低通子带系数采用PCA融合规则，带通方向子带系数采用SSIM融合规则，以得到融合图像F的Contourlet系数。

（3）对融合后的系数进行Contourlet逆变换，以产生最终的融合图像F。

图2　Contourlet变换示意图

3．1低通子带系数融合规则

Karhunen和Loeve首次提出主成分分析（principal component analysis，PCA），又名K－L变换。其数学过程是将许多个相关的变量经过一系列数学计算转换为少数几个不相关变量，这些不相关的变量称为主元成分［1，8］。主成分分析的目标是降低维数，将原来的R维空间投影到M维空间（R＞M），并且在降低维数之后保存了原始数据中的主要信息。图像的近似和平均特性主要由图像的低通子带描述，低通子带不但包含图像的主要能量，而且决定图像的轮廓。由于主成分分析能够很好地结合待融合源图像A和B相应的低通子带中的最主要信息，因此，采用二维主成分分析法进行低通子带系数融合。低通子带系数融合算法流程如下：

和一杭分手后，雪萤发现被人跟踪。她看了看那个戴墨镜的男子，不动声色地跨上一辆公交车。当她选择一个相对宽松的位置站好时，那个男子也上了车。他朝雪萤瞥了一眼，又把目光移开，钻到密集的人群中，消失了作为个体的特征，成为无数灰色背影中的一个。

（1）将待融合图像的低通子带系数矩阵以列为主序转化为一维向量X1和X2，构造数据矩阵X＝（X1X2）。

（2）计算数据矩阵X的协方差矩阵C。

xi为第i个向量的平均值。

（3）计算协方差矩阵C的特征值λi和相应的特征向量ξi，其中i＝1，．．．，m。

（4）确定加权系数ωi：

（5）计算融合图像F的低通子带系数。

3．2带通方向子带系数融合规则

带通方向子带描述了图像的亮度突变特性，图像的细节和边缘信息将受其融合效果的影响。由于带通方向子带系数与其周围8个相邻系数之间存在很大的相关性，是由区域内的多个系数共同表征和体现的。因此，提出基于区域结构相似度的带通方向子带系数融合规则，避免了单一特征量对融合结果的影响，带通方向子带系数融合算法包含以下三个步骤。

第一步：定义图像A和图像B的结构相似度（structural similarity，SSIM）［9－10］为：

其中，L（A，B）表示图像A和B的亮度比较，C（A，B）表示图像A和B的对比度比较，S（A，B）表示图像A和B的结构比较。μA和μB是图像A和B的均值，和是图像A和B的方差，σA和σB是图像A和B的标准差，σAB是图像A和B的协方差，C1，C2和C3为非常小的正常数。

第二步：定义基于区域的结构相似度，在上一步的基础之上需要定义基于区域的均值、方差、标准差和协方差，实现以各个像素为中心的区域多尺度结构相似度，其定义为：

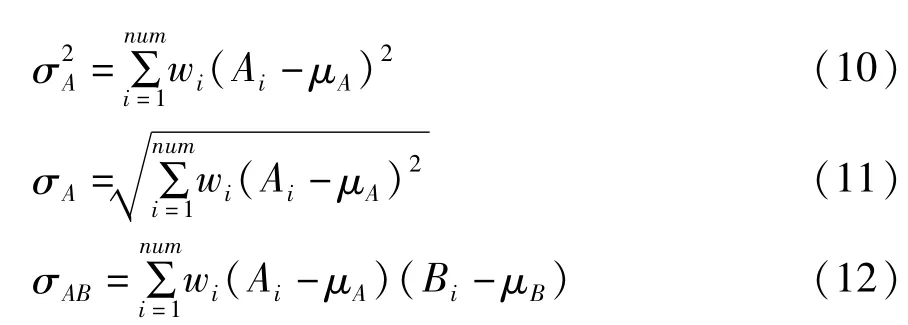
4　实验结果及分析

其中，num为将图像划分成区域的总数；w标识区域窗口函数，区域为N×N的窗口，其值之和为1；A为区域所对应图像的像素值。

第三步：定义区域结构相似度临界值为α，则融合图像F的带通方向子带系数为：

若SSIM＜α，则采用区域方差比较大的系数为融合之后的带通方向子带在此区域中心位置上的系数；

若SSIM≥α，则采用如下加权方法确定融合之后的带通方向子带在此区域中心位置上的系数。

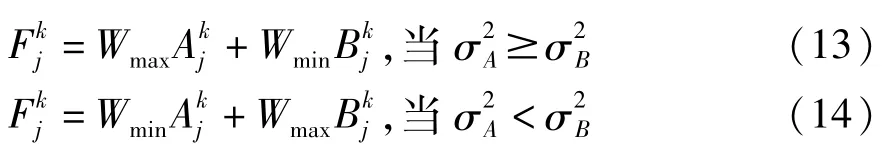
图像融合方法以Windows 7操作系统为平台，以Matlab为设计语言，针对左聚焦图像和右聚焦图像进行融合实验，实验结果如图3所示。在融合实验之前，对源图像已进行了严格的空间配准，图像大小是512×512，灰度总级数为256。图3（a）是左聚焦图像，图3（b）是右聚焦图像，采用不同的融合方法得到的实验结果见图3（c）－图3（f）。通过观察融合实验后的结果可知，图3（f）比图3（c）－图3（e）表达的图像更加清楚，图像信息更加丰富，完全能够将左聚焦图像和右聚焦图像融合成一幅左右两边均清晰的单一聚焦图像。

图3　多聚焦图像的融合

为了表明融合方法的有效性和正确性，将此方法与其他三种图像融合方法进行定量比较，并采用信息熵、相关系数和平均梯度三个客观评价标准作为定量比较的依据［11－13］。与其他融合方法相比较，该融合方法能够将熵提高2．64%～3．15%，相关系数提高0．11%～0．57%，平均梯度提高4．44%～51．4%。比较结果见表1，表1的定量比较结果和图3的结论是一致的，说明融合方法是有效的，融合结果是正确的。

5　结束语

设计了一种基于Contourlet的多聚焦图像融合方法。首先分别对左聚焦和右聚焦图像采用Contourlet变换进行分解，得到低通子带系数和带通方向子带系数，然后分别对各个子带选用PCA的融合规则或SSIM的融合规则，最后进行Contourlet逆变换得到一幅融合图像。实验结果表明，融合方法能够将多个目标的左聚焦和右聚焦图像进行融合从而生成同一目标的单一聚焦融合图像。依据客观评价标准的定量分析，融合方法在熵、相关系数和平均梯度等方面均有较为明显的改善，无论视觉效果还是客观评价均具有较好的优越性。

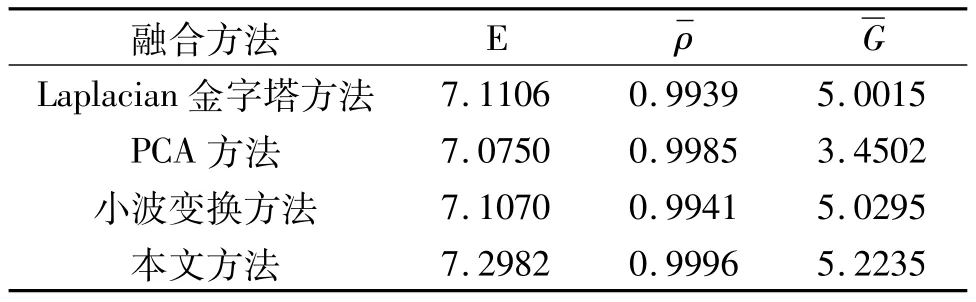
表1　融合方法的性能比较

［1］王玲，李红松，周浩，等．基于非向下采样Contourlet变换的多聚焦图像融合［J］．计算机应用与软件，2011，28（4）：196－198．Wang Ling，Li Hongsong，Zhou Hao，et al．MULTIFOCUS IMAGE FUSION BASED ON NON－SUBSAMPLEDCONTOURLETTRANSFORM［J］．Computer Applications and Software，2011，28（4）：196－198．

［2］马先喜，彭力，徐红．基于PCA的拉普拉斯金字塔变换融合算法研究［J］．计算机工程与应用，2012，48（8）：211－213．MA Xianxi，PENG Li，XU Hong．PCA－based Laplacian pyramid in image fusion［J］．Computer Engineering and Applications，2012，48（8）：211－213．

［3］郭雷，程塨，赵天云．基于小波变换和邻域特征的多聚焦图像融合算法［J］．西北工业大学学报，2011，29（3）：454－458．

Guo Li，Cheng Gng，Zhao Tanyuni．A New and Effective Multi－Focus Image Fusion Algorithm Based on Wavelet Transforms and Neighborhood Features［J］．Journal of Northwestern Polytechnical University，2011，29（3）：454－458．

［4］朱康，贺新光．基于形态学和Contourlet系数区域特征的遥感图像融合方法［J］．计算机科学，2013，40（4）：301－305．GHU Kung，HF Xin－guang．Remote Sensing Images Fusion MethodBasedonMorphologyandRegional Feature of Contourlet Coefficients［J］．Computer Science，2013，40（4）：301－305．

［5］张莹，李言俊，张科，等．基于NSCT的红外与可见光图像融合［J］．计算机工程与应用，2011，47（3）：196－198．ZHANG Ying，LI Yanjun，ZHANG Ke，et al．Fusion of infrared and visible images based on nonsubsampled Contourlet transform［J］．Computer Engineering and Applications，2011，47（3）：196－198．

［6］Do M N，Vetter li M．The Contourlet Transform：An Efficient Directional Multiresolution Image Representation［J］．IEEE Transaction on Image Processing，2005，14（12）：2091－2106．

［7］Starck J L，Candes E，Donoho D L．The Curvelet Transform for Image Denoising［J］．IEEE Transaction on Image Processing，2002，11（6）：670－684．

［8］EMMANUELJ．CANDES，XIAODONGLI．Robust Principal Component Analysis［J］．Journal of the ACM，2011，58（3）：11．1－11．37．

［9］Sourav Pramanik，Swagatika Prusty，Debotosh Bhattacharjee，et al．A Region－to－Pixel Based Multi－sensor Image Fusion［J］．International Conference on Computational Intelligence：Modeling，Techniques and Applications，2013，10：654－662．

［10］Ashirbani Saha，Gaurav Bhatnagar，Q．M．，et al．Mutual spectral residual approach for multifocus image fusion［J］．Digital Signal Processing，2013，23：1121－1135．

［11］王建，刘肖，王国珲．基于梯度变换的多传感器图像融合算法［J］．重庆理工大学学报（自然科学），2012，26（10）：62－65．WANG Jian，Liu Xiao，WANG Guo－hui．Multi－Sensor Image Fusion Algorithm Based on Gradient Transform［J］．Journal of Chongqing University of Technology（Natural Science），2012，26（10）：62－65．

［12］王建，刘肖，王国珲．基于区域能量的多聚焦图像融合算法［J］．陕西理工学院学报（自然科学版），2012，28（5）：39－43．WANG Jian，LIU Xiao，WANG Guo－hui．Multi－focus image fusion algorithm based on regional energy［J］．Journal of Shaanxi University of Technology（Natural Science Edition），2012，28（5）：39－43．

［13］王建，王必宁，杨根善，等．基于形态学金字塔的医学图像融合技术［J］．兵工自动化，2014，33（1）：82－84．Wang Jian，Wang Bining，Yang Genshan，et al．Fusion Technology of Medical Image Based on Morphological Pyramid［J］．Ordnance Industry Automation，2014，33（1）：82－84．

Approach of Image Fusion Based on Contourlet Transform

Wang Jian1，Wang Bining2，Hou Weigang1
（1．School of Computer Science，Xi'an Aeronautical University，Xi'an 710077，China；2．Xi'an Thermal Power Research Institute Co．，Ltd．，Xi'an 710032，China）

Focusing on the problem of the fusion of the left－focus image and right－focus image from the same scene，a novel multi－focus image fusion approach based on contourlet transform is designed．Firstly，the contourlet transform is used to perform the multiscale and multidirection decomposition of the source images．Secondly，low frequency subband coefficients and bandpass directional subband coefficients of the fused image can be obtained by the fusion rules based on principal component analysis（PCA）and region structural similarity．Finally，the fused image is reconstructed by performing the inverse contourlet transform on the combined coefficients．The results of experiment and quantitative analysis demonstrate that the proposed algorithm can fuse into a clear single focus image，and the proposed algorithm is superior with entropy improvement from 2．64%to 3．15%，correlation coefficient enhancement from 0．11%to 0．57%and average gradient improvement from 4．44%to 51．4%．

Multi－focus images；Contourlet transform；Principal Component Analysis（PCA）；Structural similarity；Image fusion；Fusion rules

10．3969／j．issn．1002－2279．2016．05．011

TP39

A

1002－2279（2016）05－0043－05

❋陕西省光电测试与仪器技术重点实验室开放基金资助（ZSKJ201408）

王建（1976－），男，陕西省渭南市人，硕士研究生，讲师，主研方向：图像融合、计算机视觉等方面的研究。

2016－03－21