基于模糊逻辑理论的前馈控制器设计方法研究

张彦龙，张 驰，赵 飞，杜文华，柳 瑞,马 骏

(1.中国科学院 宁波材料技术与工程研究所， 宁波 315201；2.中北大学， 太原 030051)



基于模糊逻辑理论的前馈控制器设计方法研究

张彦龙1,2，张 驰1，赵 飞1，杜文华2，柳 瑞1,马 骏2

(1.中国科学院 宁波材料技术与工程研究所， 宁波 315201；2.中北大学， 太原 030051)

永磁直线电机在变速运行时会产生较大的位置跟踪误差，严重影响直线电机的动态跟踪精度。运用模糊逻辑理论设计前馈控制器是实现降低系统位置跟踪误差的重要手段之一。首先在MATLAB/Simulink中搭建位置闭环、速度闭环和电流闭环三环控制器。为降低电机在运行时的振动，将S曲线作为指令信号加入到系统中，根据前期电机调试经验并结合模糊逻辑理论设计前馈控制器，实现降低直线电机运行时的位置跟踪误差。仿真和实验结果表明，模糊逻辑前馈控制器的加入有效地降低了系统运行时的位置跟踪误差。

永磁同步直线电机；前馈补偿；模糊逻辑前馈控制器；S型曲线

0 引 言

永磁同步直线电机在高速高精度定位系统中的应用日益增多。永磁同步直线电机使得系统的传动链得到简化，减少了因传动链而引入的误差，避免了滚珠丝杠传动中的反向间隙、惯性、摩擦力和刚度不足等缺点，提高了定位系统运行时的速度及加速度，拓宽了控制带宽范围，积极推动了高速高精密加工的发展。

直驱进给系统若只采用负反馈控制，可以在一定程度上减小误差，但由于系统的控制带宽和增益会受其机械结构本身的限制，大大增加了其应用到高速高精度场合的难度。因此，将前馈控制引入到负反馈系统中以提高系统的控制精度是非常必要的。零相位误差跟踪控制 (ZPETC)[1-3]可以消除反馈环的所有极点以及可以消除的零点，并且可以消除不可消除的零点所引起的相位误差，使得期望输出到实际输出的频率响应相位变化为零，极大地减小了系统的跟踪误差。当反馈控制器和控制对象模型阶数较高时，设计出的零相位误差跟踪控制器就会有非常高的阶数。此时，该控制器很难应用于实时控制系统中。当干扰信号影响控制系统时，零相位误差跟踪控制器会放大命令信号中的高频成分或放大部分噪声，产生高频扰动。重复学习[4-6]主要应用于因非线性对象模型和参数不确定性所引起的跟踪控制问题，通过不断地学习，改善系统控制的性能。由于重复学习需要特定系统和同样的初始条件，而控制系统具有多样性，使得学习控制算法收敛性具有很大的局限性。因此，重复学习主要应用在不基于模型的低速控制系统中，在要求强实时性的控制系统中应用难度较大。张刚和潘霞远等人[7-8]提出了将指令速度信号和加速度信号分别乘上一个合适的系数作为前馈量加入到控制系统中，虽然提高了轨迹跟踪精度，但在变速区电机的轨迹跟踪精度仍然很大。线性与指数加减速算法在变速阶段会出现加速度突变现象，该现象会使生成的速度曲线不够平滑。不平滑的指令加速度信号容易在轨迹生成中产生高频扰动分量，该分量会引起直驱进给系统不必要的振动。为得到平滑的速度和位置轨迹指令曲线，降低电机运行时的振动，本文采用S型曲线作为位置指令信号[9]。模糊控制器在设计中不需要受控对象精确的数学模型，使得控制策略易于理解，设计简单并便于应用。模糊控制系统具有较强的鲁棒性，外界干扰对其控制的影响被大大削弱了，尤其适用于非线性、时变和具有滞后系统的控制。本文结合模糊逻辑理论，设计出了模糊前馈控制器，有效提高了电机运行时的位置跟踪精度，尤其是电机在指令信号作用时的位置跟踪精度。

1 传统复合前馈控制器的设计

本文首先以永磁同步直线电机为被控对象，建立位置闭环、速度闭环和电流闭环三环控制器。其中，电流环采用id=0矢量控制方式。此时，电机的输出电流和电机产生的推力成正比。永磁同步直线电机的动力学方程可表示：

(1)

(2)

式中：F为电磁推力；m为电机动子质量；a为电机的加速度；kv为电机的粘滞系数；v为电机的运行速度；K为电机推力常数；iq为电机的q轴电流。

由式(1)和式(2)可知，永磁同步直线电机速度的产生，粘滞阻力的克服以及其他干扰因素的抑制主要由q轴电流来提供。负反馈是根据系统的指令与实际的误差值进行控制的，输出量发生变化形成误差值进而负反馈系统产生控制作用。故反馈控制会导致系统响应滞后。当对系统的速度和精度要求不高时常采用此类控制，但对电机的响应速度和精度要求较高时，单纯的反馈控制便不能满足要求。将指令速度信号和加速度信号分别乘上一个合适的系数作为前馈量加入到控制系统中，可以有效提高系统的响应速度，弥补负反馈牺牲系统响应速度来抑制扰动的缺点。常用伺服控制前馈算法框图如图1(a)所示。根据前期工作的经验总结，复合前馈增益的初值按以下原则选取:

(3)

(4)

式中：kv为滑动粘滞系数；k为电磁力常数；m为动子的质量。

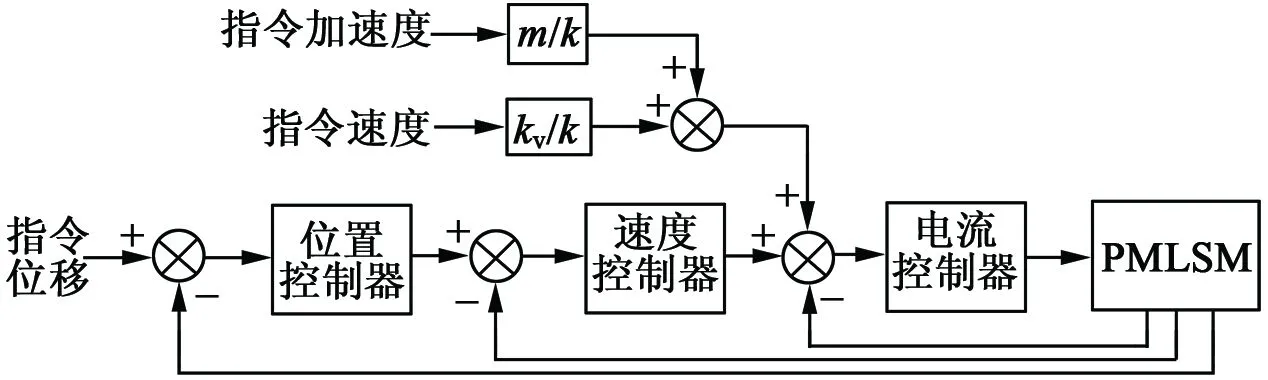
(a) 常用前馈控制图

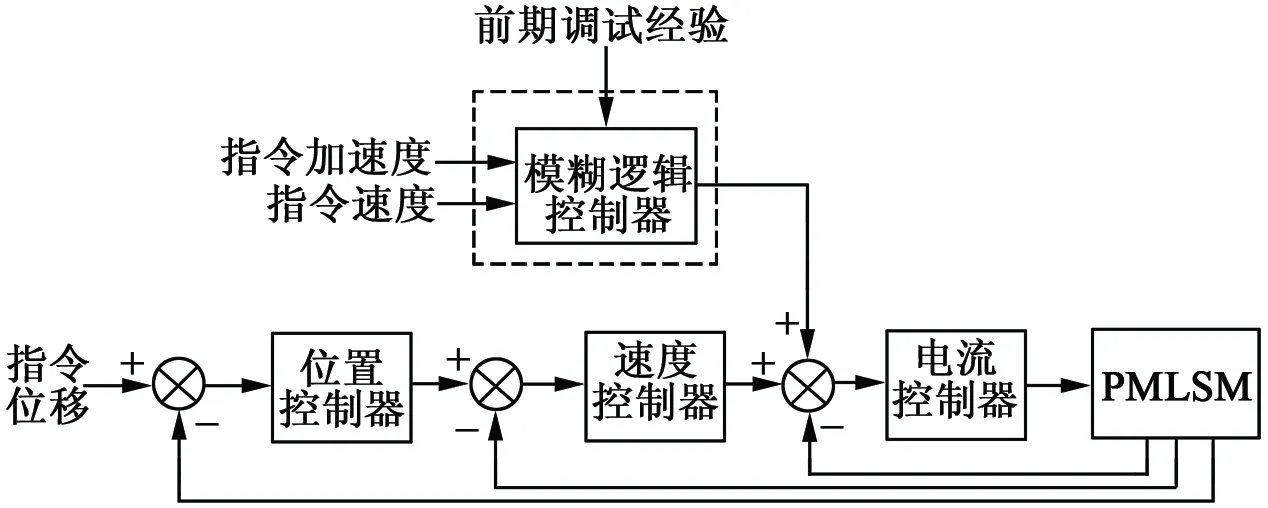
(b) 模糊前馈控制图

图1 伺服控制系统框图

2 模糊逻辑前馈控制器的设计方法

模糊控制器的系统框图如图2所示。由图2易知，本文设计的模糊控制器具有指令速度v0和指令加速度a0两个输入变量；V0和A0为对应的模糊量；U为输出模糊量；u为控制器作用到系统中的输出精确量。

图2 模糊控制过程

对于指令速度，本文采用NB，NM，NS，ZO，PS，PM和PB等7个语言变量来描述，指令加速度由N，Z和P等3个语言变量来描述。隶属函数采用三角形隶属函数来表示，曲线形状如图4所示。

本文模糊控制规则的句型运用“ifV0andA0thenU”的形式。每条模糊语句均对应了一个模糊关系Fi。各模糊语句之间存在“或”关系，故模糊控制规则总的模糊关系：

(5)

若将模糊量V0及A0带入模糊规则，则求得U的表达式：

(6)

式中：“∨”表示取两数最大，“×”表示直积， “∘”为关系合成运算。模糊关系定义为，设U，V为论域，若R∈F(U∘V)，称R为U到V的模糊关系。

本文的模糊控制器采用Mamdani推理合成算法，其最大的特点是将模糊蕴含关系A→B表示为直积的形式，即:

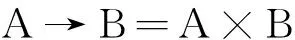
(7)

本文基于Mamdani法并结合前期的调试经验制定的模糊控制规则如表1所示。每条模糊语句均代表针对某一确定情况的应对方法。

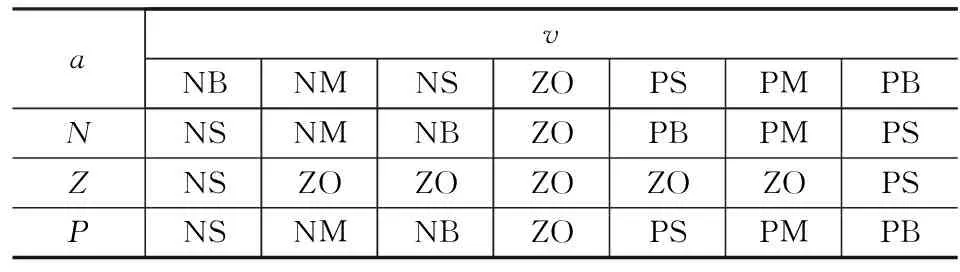
表1 模糊控制规则表

通过仿真和实验分析发现，隶属函数的形状和分布规律会对控制输出产生影响，尤其是邻近的隶属函数间的重叠度会对控制器的性能产生较大影响。重叠指标的定义如式(8)所示，图示如图3所示。若邻近的隶属函数不重叠会导致控制性能下降，甚至会出现控制死区。重叠率越大、重叠鲁棒性越强，模糊控制器抵抗特性参数变化的能力越强，控制灵敏度越低，反之亦然。因此，对于比较复杂的被控对象，选用一组固定重叠率值的三角隶属函数时控制效果并非最佳。本文采用的模糊逻辑方法根据不同阶段的控制结果，通过调整隶属函数的斜率，即整定重叠率，使控制器控制效果更好，可调斜率隶属函数曲线如图4所示。由于本实验需要对斜率参数在线实时调整，而模糊工具箱中的参数不能在dSPACE的Controldesk界面中在线实时调整，故本文的模糊控制器在MATLAB中编写并加载到dSPACE中。

c=(重叠范围)/(两相邻隶属函数覆盖范围) (8)

图3 重叠率计算图

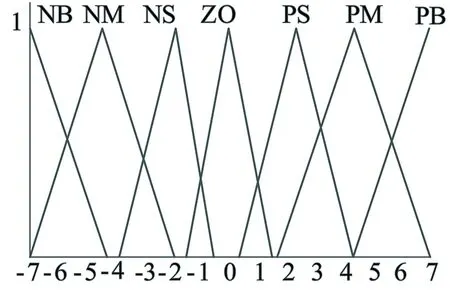
图4 可调斜率的三角形隶属函数曲线

3 基于模糊逻辑前馈控制器的仿真实验及结果讨论

3.1 S型轨迹曲线的设计

S型曲线指的是直驱进给系统在变速阶段时的速度曲线为S型。S曲线在变速时的加加速度的值为常数，适当的调整加加速度值可以有效的减小给机械系统造成的冲击。同时，针对不同的被控对象，设定加速度和加加速度两个值可实现柔性加减速控制。本文电机的运行位移为0.05 m，最大速度为0.3 m/s，最大加速度为3.82 m/s2，加加速度为48 m/s3。

3.2 仿真实验及结果分析

本文在MATLAB/Simulink环境中建立位置闭环、速度闭环和电流闭环控制系统，仿真对象为永磁同步直线电机，其参数如表2 所示。根据上述的原理可以设计出模糊逻辑前馈控制器，其理论框图如图1(b)所示。电机的运行轨迹如图5所示，其控制结果如图6所示。由图6可以看出，当系统无前馈控制时，系统的位置跟踪误差较大；当系统加入传统前馈时的位置跟踪误差的最大值为16.64 μm；当系统加入固定斜率模糊逻辑前馈控制器时的最大位置跟踪误差为2.15 μm；当系统加入可调斜率模糊逻辑前馈控制器时的最大位置跟踪误差降为1.7 μm。由此可得，由可调斜率模糊逻辑前馈控制器补偿后的位置跟踪误差较传统前馈补偿后的位置跟踪误差降低了90%以上，且当指令信号结束后系统以更短的时间进入到-1～1 μm的区间内。由该图还可以看出，可调斜率模糊逻辑前馈控制器补偿后的位置跟踪误差较传统前馈补偿的最大位置跟踪误差降低了近0.5 μm。验证了本文提出的可调斜率模糊逻辑前馈控制器的可行性。应当指出的是，由于模糊控制规则为有限数量的原因，使得系统的位置跟踪误差不能被完全抑制。

图5 S曲线加减速过程

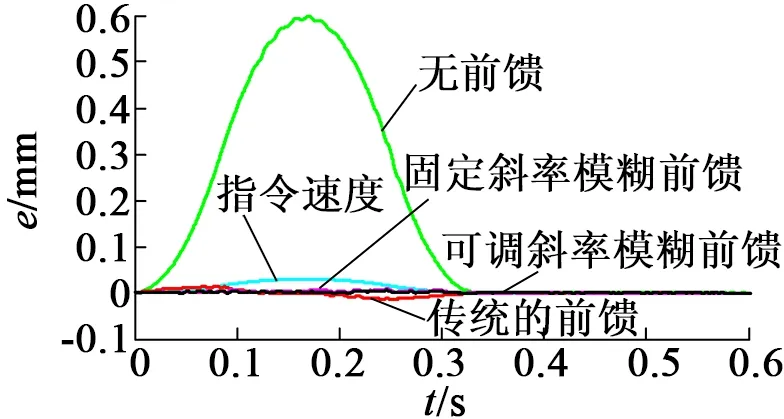
(a) 加入前馈补偿前后对比

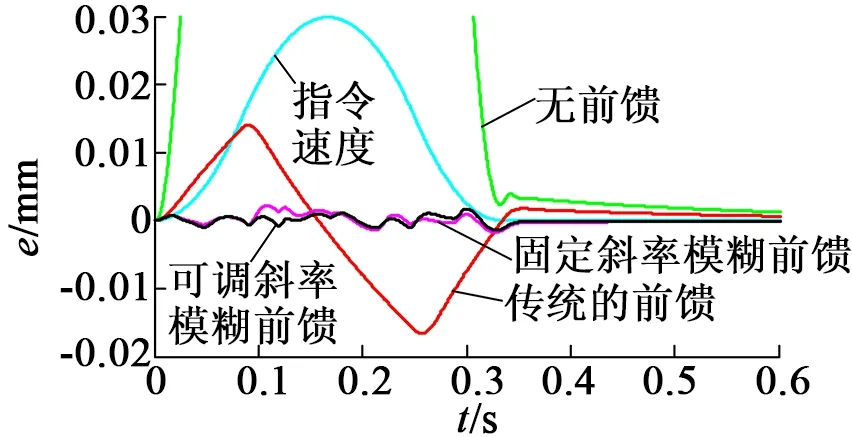
(b) 加入不同前馈补偿对比

图6 补偿前后及不同补偿方法下的位置跟踪误差曲线

4 基于模糊逻辑前馈控制器的补偿实验及结果讨论

4.1 实验配置

论文提出的模糊逻辑前馈控制器方法被应用在一台XY直线电机，其Y向电机作为被控对象。该方向直线电机相关参数如表2所示。位移由MicroE MII30型号的光栅尺测量，其测量精度为0.4 μm。试验台控制器由dSPACE1103控制开发系统搭建，驱动器采用Copley Xenus型驱动器，电机的冷却由图中所示的空气压缩机提供。整个永磁同步直驱电机伺服系统平台如图7所示。

图7 实验配置

4.2 模糊逻辑前馈补偿实验及结果讨论

在MATLAB/Simulink中搭建电机的位置闭环和速度闭环控制器，并将其加载到dSPACE1103中，结合Copley Xenus驱动器使电机按照预设的轨迹运行。首先在Simulink中编写模糊逻辑前馈控制器模块的程序并将其加载到dSPACE1103中以实现实时调整。本实验的输入轨迹仍按上节给出的S型轨迹，其最大的运行速度为300 mm/s。从图8(a)可以看到，在未加入前馈补偿时，直线电机运行时的位置跟踪误差比较大，加入前馈补偿后的位置跟踪误差被明显抑制。由图8(b)可知，加入传统前馈补偿时的位置跟踪误差为15.45 μm；加入固定斜率模糊前馈补偿后的位置跟踪误差为8.3 μm；加入可调斜率模糊前馈补偿后，其位置跟踪误差降为5.3 μm。从实验结果可以看出，可调斜率模糊前馈补偿后的位置跟踪误差较传统前馈补偿降低了60%以上。同时，可调斜率模糊逻辑前馈控制器补偿后的位置跟踪误差较固定斜率模糊前馈补偿的位置跟踪误差明显降低。应当指出的是，仿真所用的被控对象的数学模型和电机的实际模型有一定差异，导致仿真结果和实验结果略有不同；电机在运行时所受噪声及振动的影响，使得补偿后的位置跟踪误差波动较大。同时，电磁推力常数随着位置变化也会略有不同，导致电磁推力和q轴电流并非呈严格的正比关系，电磁推力的非线性也会引起电机的位置跟踪误差的波动。论文的下一步工作将电磁推力常数变化的影响也加入到补偿系统中，并降低电机运行时的噪声影响，使得补偿效果更好。

(a) 加入前馈补偿前后对比

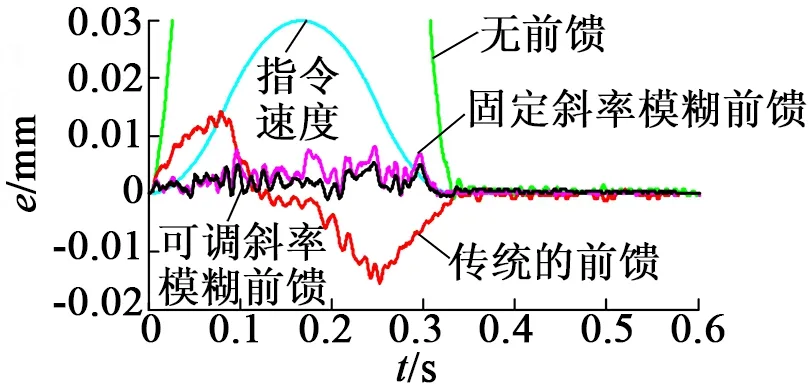
(b) 加入不同前馈补偿对比

图8 补偿前后及不同补偿方法下的位置跟踪误差曲线

5 结 语

针对电机在变速运行时存在较大的位置跟踪误差，本文建立了基于模糊逻辑理论的前馈补偿策略。首先搭建位置闭环、速度闭环和电流闭环三环控制器。然后为减小电机运行时的振动，使电机按照S型轨迹运动，最后根据电机运行时的位置跟踪误差设计模糊逻辑前馈控制器。通过一台XY永磁同步直驱电机的实验研究表明，该方法明显抑制了指令信号作用时的位置跟踪误差，一定程度上减小了指令信号结束后的位置误差降到-1～1 μm的时间。同时该方法实现过程较为简单，不需要额外的实验设备和传感器，实时性强。

[1] 陈兴林,刘川,周乃新,等.基于ZPETC-FF和DOB的精密运动平台控制[J].哈尔滨工业大学学报,2014，46(1)：1-6.

[2] 李志军,刘成颖,孟凡伟,等.基于ZPETC和DOB的直线电机控制器设计及实验研究[J].中国电机工程学报,2012,32(24):134-140.

[3] KAMIGAKI Y,OHISHI K,NABATA Y,et al.Zero phase error tracking control system with multi harmonics disturbance suppression loop[C]//11th International Workshop on Advanced Motion Control,AMC.2010:377-382.

[4] ROTARIU I,STEINBUCH M,ELLENBROEK R.Adaptive iterative learning control for high precision motion systems[J].IEEE Transactions on Control Systems Technology,2008,16(5):1075-1082.

[5] HELFRICH B E,LEE C,DOUGLAS A B,et al.Combined H∞-feedback control and iterative learning control design with application to nanopositioning systems[J].IEEE Transactions on Control Systems Technology,2010,18(2):336-351.[6] 蔡满军,赵成圆.永磁直线同步电机的自适应迭代学习控制[J].微特电机，2013，42(6):48-54.

[7] 张刚,刘品宽,张波,等. 直线电机精密运动平台轨迹跟踪控制器设计[J].光学精密工程,2013,21(2):371-379.

[8] 潘霞远. 高精度永磁直线伺服系统的研究[D].广州：广东工业大学,2008.

[9] 张碧陶,高伟强,沈列,等.S曲线加减速控制新算法的研究[J].机床与液压,2009,37(10):27-29.

[10] 林辉,吕帅帅,樊明迪.基于模糊前馈的永磁同步电动机滑模矢量控制系统[J].微特电机,2013,41(4):35-37.

[11] 朱尔立,舒志兵,沈阳,等.基于模糊控制的激光加工间隙控制设计分析[J].机械设计与制造,2015(8):13-15.

[12] CAZAREZ-CASTRO N R,MALDONADO Y.Design and hardware implementation of a closed-loop stable fuzzy controller[C]//2014 11th International Conference on Electrical Engineering,Computing Science and Automatic Control (CCE),IEEE,2014:1-6.

[13] AKBAR M A.Simulation of fuzzy logic control for DC servo motor using Arduino based on MATLAB/Simulink[C]//2014 IEEE International Conference on Intelligent Autonomous Agents, Networks and Systems (INAGENTSYS),IEEE,2014:42-46.

Research of the Design of Feedforward Controller Based on Fuzzy Theory

ZHANGYan-long1,2，ZHANGChi1，ZHAOFei1，DUWen-hua2,LIURui1,MAJun2

(1.Ningbo Institute of Industrial Technology,CAS,Ningbo 315201,China；2.North University,Taiyuan 030051,China)

Position tracking error will occur when permanent magnet linear motor is moving, especially working with variable speed.The error influences the dynamic tracking accuracy of linear motor seriously. Feedforward controller designed by using fuzzy logic theory is one of the important means to reduce system position tracking error. First, position closed-loop, speed closed-loop and current closed-loop controller were built in the MATLAB/Simulink. In order to reduce the vibration of the motor when it was running, the S curve was treated as the command signal. According to the experience of adjusting the motor earlier and the fuzzy logic theory, feedforward controller was designed to lower position tracking error of the linear motor when it was working. Simulation and experimental results show that the feedforward fuzzy logic controller effectively reduces the system position tracking error at runtime.

permanent magnet synchronous linear motor; feedforward compensation; feedforward fuzzy logic controller; S curve

2015-09-17

国家自然科学基金项目(51207158)；国家自然科学基金项目(51405479)；中国博士后科学基金项目(2015T80639)；宁波市创新团队(2012B82005)；宁波市重大专项(奥马特)(2013B-10042,2013B10043)；中科院百人计划(2015A610146,2015A-610154)；宁波市自然科学基金项目(2014A610084)

TM351;TM359.4

A

1004-7018(2016)06-0001-04

张彦龙(1990-)，男，硕士研究生，研究方向为电机控制。