基于乘客出行时间最短的有轨电车站点规划及建模

李鹏凯

(1. 深圳市城市交通规划设计研究中心有限公司 广东深圳 518021；2. 深圳市交通信息与交通工程重点实验室 广东深圳 518021)



基于乘客出行时间最短的有轨电车站点规划及建模

李鹏凯1,2

(1. 深圳市城市交通规划设计研究中心有限公司 广东深圳 518021；2. 深圳市交通信息与交通工程重点实验室 广东深圳 518021)

当前我国有轨电车系统的规划缺少相应的技术规范和标准，而地铁或常规公交规划方法难以适应有轨电车的特点。基于以人为本的公交优先理念，在深入分析乘客出行过程的基础上，以乘客加权平均出行时间最小为优化目标，建立乘客出行时间与站点方案的数学关系模型。同时，依托东莞市有轨电车首期线路规划研究课题，将模型应用于实际规划案例中。应用结果表明，该有轨电车站点规划模型可有效缩短乘客平均出行时间，提高有轨电车服务水平。

有轨电车；竞争力；出行；公交优先；站点规划

有轨电车作为中运量公共交通工具，相对于大运量轨道交通，具有造价低、投资少、工期短、见效快、绿色环保等优点，同时可提供接近于地铁水平的服务，因此近年来日益受到国内大中城市决策者的青睐。目前，国内近10座大中城市已开通或即将开通现代有轨电车线路，同时10余座城市已开工建设或计划建设现代有轨电车。

1 研究现状

近年来，国内外针对有轨电车的学术研究逐渐深入，由最初的车辆制式研究、系统特点分析、成功经验介绍，逐步深入至规划方案、交通设计、信号优先控制等方面。

覃矞[1]、张国华[2]、张子栋[3]等均从有轨电车运量适中、敷设灵活、运营组织灵活等特点出发，提出有轨电车线路规划应遵循与地铁有效衔接、发挥网络效益、满足城市建设重点片区需求、与其他交通方式协调、灵活组织运营等规划原则。

宗传苓[4]、王远回[5]、王英杰[6]、黎东平[7]、左璇[8]分别结合深圳、沈阳、苏州、重庆等地有轨电车相关规划研究课题，介绍了该城市有轨电车线路特征、规划原则及发展方向。

综合国内外的研究现状可以看出，目前对于有轨电车规划方面的研究多集中于线路规划和线网规划，对站点规划方法研究仍处于探索阶段，实际应用中多采取与地铁或常规公交类似的规划方法。然而，有轨电车在站点有效覆盖范围、服务水平、运营灵活性等方面与地铁、常规公交均存在相当差异，采用类似的规划方法难以有效发挥有轨电车的功效。笔者围绕提升有轨电车竞争力的核心目标，基于出行的公交优先为规划理念，提出有轨电车站点规划模型，以最大限度降低沿线居民出行的时间，提高有轨电车的服务水平。

2 问题描述

提高有轨电车系统竞争力是国内外有轨电车系统规划、设计、管理的共同目标，其主要体现于便捷性、可达性、可靠性、舒适度等方面。由于国内外有轨电车多采用100%或70%低地板列车，车辆沿固定轨道行驶，且拥有一定的路权优先，在可靠性、舒适性方面具备先天优势，因此在满足一定覆盖水平的基础上，有轨电车站点规划的核心为提高乘客出行的便捷性，即降低乘客乘坐有轨电车的总出行时间。

如图1所示，乘客单次乘坐有轨电车出行的过程可以分为4部分： 1) 出发地/其他交通方式衔接点→电车站点； 2)电车站点候车； 3)乘车出行； 4)电车站点→目的地/其他交通方式衔接点。

图1 基于出行的公交优先

相应地，乘客单次乘坐有轨电车的出行时间由以下4部分组成：

1) 乘客从出发地(包括有轨电车车站周边建筑出入口及换乘点)到达车站的步行时间；

2) 乘客在车站的候车时间；

3) 乘客从上车到下车的乘车时间；

4) 乘客从站点到达目的地(包括有轨电车车站周边建筑出入口及换乘点)的步行时间。

在其他外部条件均相同的情况下，站点间距愈小，意味着车站对沿线的覆盖率愈高，乘客的步行时间愈短；然而，站点间距愈小，同时意味着有轨电车启停愈加频繁，乘客的乘车时间愈长(见图2)。

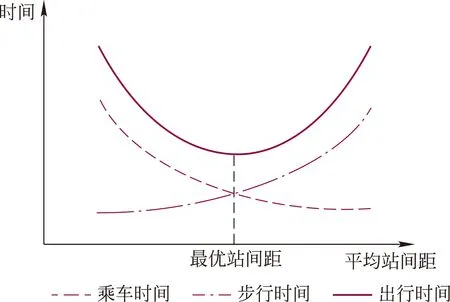
图2 研究原理

基于此原理，本研究的基本思路是：分别建立乘客步行时间、乘车时间与站点方案的关系模型，从而以定量分析的手段对比不同站点方案的乘客加权平均出行时间，进而获得最优的站点规划方案。

3 站点规划模型

3.1 基本假设

为聚焦研究对象，锐化研究问题，本研究基本假设如下：

1) 有轨电车线路的服务对象为线路两侧500 m范围内所有出行者；

2) 站点规划方案的变化，对线路运营组织方案不造成影响；

3) 站点规划方案的变化，对线路总体客流的影响可忽略不计。

3.2 优化目标函数

为提高有轨电车的竞争力，有轨电车站点规划的目的为尽可能降低乘客的平均出行时间，站点规划模型的优化目标函数为

式中：s为有轨电车线路站点规划方案编号；i，j均为线路沿线车站编号，i，j=1，2，…，Ns；Ns为规划方案s的总车站数；(i，j)为i车站与j车站之间的OD；Rs为规划方案s的OD集合；pij为i站点到j站点的客流量；αij为i站点到j站点的加权系数；P为线路总客流量，即

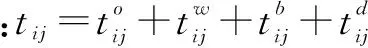
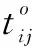
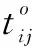
式中：dik为i车站k小区距离i车站的步行距离；vik为i车 站k小区达到i车站的步行速度，一般情况下该速度值可取固定值或范围值，可根据实际调查获得；pik为i车站k小区抵达i车站的上客量；βik为i车站k小区乘客的加权系数；Pi为i车站的总上客量，其为车站范围内所有小区到达车站的客流总量，即

有轨电车线路客流量为所有车站上客量之和，即

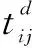
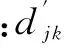
有轨电车线路客流量为所有车站下客量之和，即

3.3 约束条件

为减少模型计算的复杂性，更快速地得出优化结果，站点规划模型的约束条件如下：

3.3.1 最大车站间距约束

为保障有轨电车线路对沿线居民的覆盖，应对有轨电车相邻站点最大间距加以约束：Di≤Dmax，Di为i车 站与i+1车站的距离；Dmax为最大站点间距。

根据有轨电车规划经验，一般情况下，相邻站点间距应小于1 km；若线路需途经大型居住社区或居民稀疏片区，则站间距可适当加长。

3.3.2 最小车站间距约束

相对于一般机动车而言，有轨电车启动、制动加速度相对较小，若车站间距过小，有轨电车出站后尚未加速至最高车速，就需减速进站，导致有轨电车行驶时间过长。

根据对国内某厂家制作有轨电车车辆牵引模拟计算可得，有轨电车在最高车速60 km/h情况下，若相邻站点站间距小于350 m，则有轨电车无法加速至最高车速，行程速度相对较低。如图3所示，当站间距为600 m时，有轨电车区间运行时间需50 s，区间平均行驶速度为43 km/h；而当站间距为350 m时，有轨电车区间运行时间需37 s，区间平均行驶速度为34 km/h，行驶速度降低约21%。

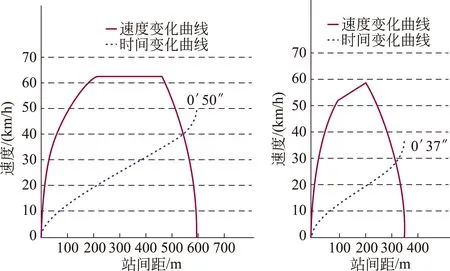
图3 不同站间距情况下有轨电车牵引模拟情况

因此，为避免有轨电车区间行驶速度过低，应对站点最小间距加以约束：Dmin≤Di，式中Dmin为最小站点间距，具体数值可视有轨电车车辆性能而定。

3.4 模型求解

一般情况下，有轨电车线路站点较多，若对线路每种站点组合均进行分析计算，则运算量较大，不利于实际规划项目应用。因此，在实际应用中，应根据客流分布、道路条件、交通组织等，结合规划设计经验，排除明显不合理规划方案，尽可能缩小规划方案的范围，以便于规划模型的求解。

同时，对于线路较长、车站较多的线路，可将线路进行分段，利用优化模型分别对每段的站点方案进行求解，进而得出最终优化方案。

4 实际应用

为加强科学理论与实践工作的联系，本文结合东莞市现代有轨电车首期线路规划研究，对站点规划模型进行验证。

东莞市现代有轨电车首期线路南起东莞市南城CBD核心区，沿市中心区主要道路敷设，北至东莞市汽车东站附近，线路全长约12 km。线路同时承担东莞市中心城区内部出行功能及接驳衔接轨道线路功能，目前线路处于规划设计阶段(见图4)。

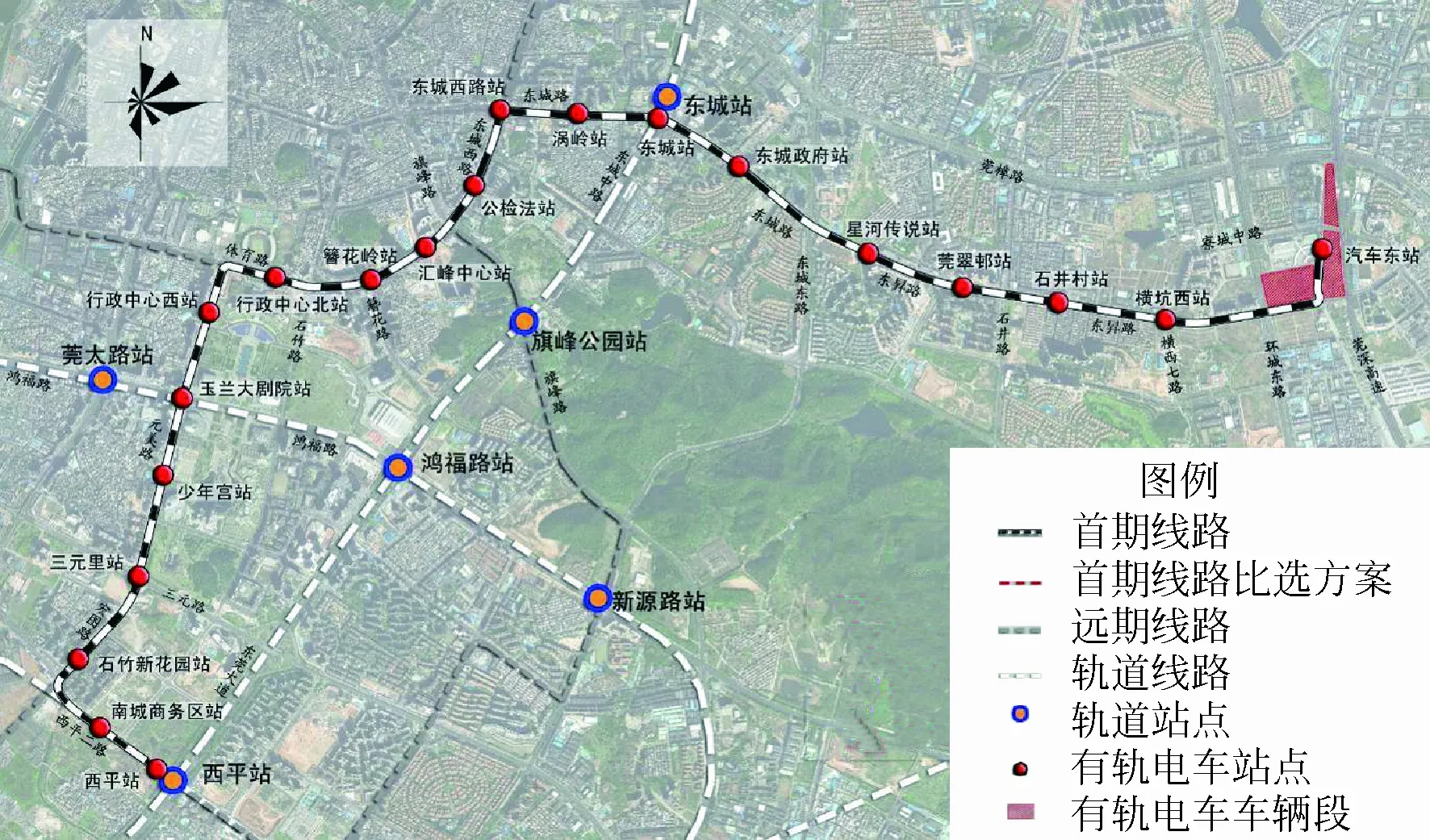
图4 东莞有轨电车首期线路走向

重点针对东莞首期线路东城西路段进行研究，结合道路条件、交通组织等因素，对站点规划方案进行初步分析，提出2种站点规划方案，方案差异在于站点数及具体站点位置的不同，具体方案如图5所示。

图5 东莞有轨电车首期线路比选方案

不同方案预测客流OD分布情况如表1、2所示。

表1 方案1客流OD分布 人次/d

根据客流分析可得，以上2种站点规划方案影响的乘客包括2类：

表2 方案2客流OD分布 人次/d

1) 起点或终点在2种规划方案不同站点之间的乘客，即表中深色部分；对于该部分乘客，不同方案的乘客步行时间及乘车时间均不同；

2) 出行路线包含2种规划方案不同区段的乘客；对于该部分乘客，仅不同方案的乘车时间不同。

对于其他乘客，站点规划方案调整对其基本不造成影响。

通过对2种规划方案乘客出行时间进行对比分析可得，方案2通过增加站点，可有效降低东城西路段乘客的出行时间，但途径乘客的出行时间有所增加。2种方案不同站点间的乘客平均出行时间如表3、4所示。

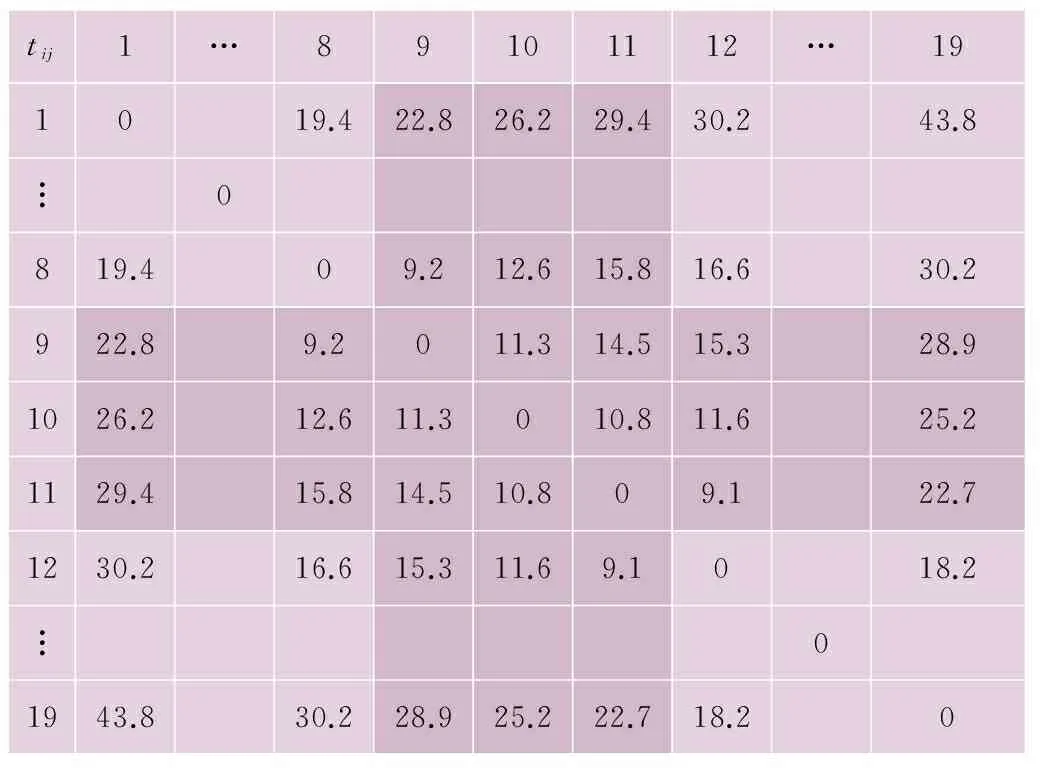
表3 方案1不同站点出行时间汇总 min

根据本文站点规划模型计算分析可得，方案2乘客平均加权出行时间降低10%左右，故确定为推荐方案。

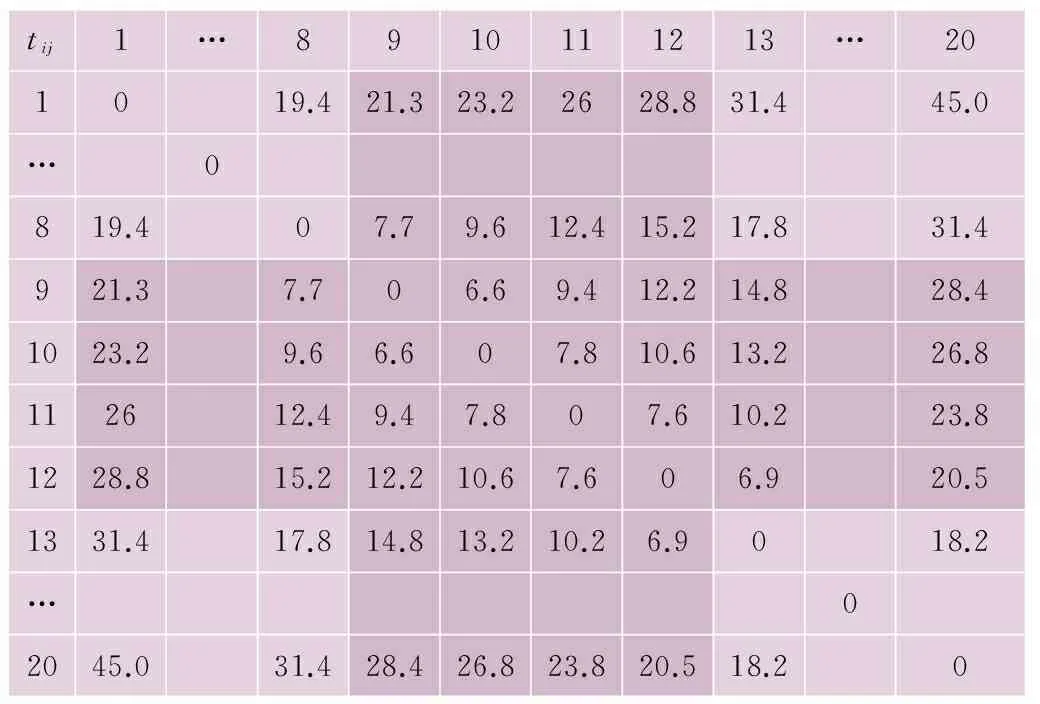
表4 方案2不同站点出行时间汇总 min

5 结论

本文在深入分析乘客出行过程的基础上，建立乘客出行时间与站点方案的数学关系模型，并将模型应用于实际规划案例中。应用结果表明，本文所提出的有轨电车站点规划模型，可有效缩短乘客平均出行时间，提高有轨电车服务水平。同时，本规划模型可为快速公交等其他交通方式规划提供参考。

[1] 覃矞，戴子文，陈振武.现代有轨电车线路规划初探[J].都市快轨交通，2013，26(2)：42-45.

[2] 张国华，欧心泉，周乐，等.有轨电车系统规划设计思考[J].城市交通，2013(4):24-29.

[3] 张子栋.有轨电车系统规划设计研究[J].城市交通，2013(4):31-38.

[4] 宗传苓，王远回.深圳市龙岗区现代有轨电车规划研究[C]//中国城市交通规划2012年年会论文集，2012:1200-1207.

[5] 王远回，宗传苓，刘永平.深圳市现代有轨电车发展策略[J].城市轨道交通研究，2014,17(6)：11-16.

[6] 王英杰，王婧一.沈阳现代有轨电车系统规划建设要点[J].城市轨道交通研究，2014,17(2)：125-128.

[7] 黎冬平，王宝辉，唐淼.苏州高新区有轨电车线网规划方案与要点研究[J].江苏城市规划，2014(2)：30-33.

[8] 左璇，王鹏.重庆主城区现代有轨电车线网规划研究[J].交通建设与管理，2014(24)：281-285.

(编辑：曹雪明)

Trams Site Planning and Modeling Based on Passengers’Shortest Travel Time

Li Pengkai1，2

(1. Shenzhen Urban Transport Planning Center Co., Ltd., Shenzhen 518021;2. Shenzhen Key Laboratory of Traffic Information and Traffic Engineering, Shenzhen 518021)

The current planning of tram system in China is lack of specific technical specifications and standards, and the subway or conventional public transport system planning method is difficult to be applied to tram system planning because the tram system has different characteristics. In line with the principle of giving priority to developing people-centered public transport system, the paper makes an in-depth analysis of passenger travel process, and by taking the weighted minimum average passenger travel time as the optimization goal, a mathematical relationship model of passenger travel time and site plan is established. At the same time, research is done on the planning of the first line of Dongguan tram in Guangdong province and the model has been applied to practical planning cases. The application results show that the present tram site planning model, which can effectively shorten the average passenger travel time, improves the level of tram service.

tram; competitiveness; travel; public transport priority; site planning

10.3969/j.issn.1672-6073.2016.05.025

2015-10-19

李鹏凯，男，硕士，工程师，研究方向为交通规划、交通设计,lipengkai1990@163.com

U482.1

A

1672-6073(2016)05-0120-05