高速列车轴箱圆锥滚子轴承滚动体的对称修形

魏延刚，许凯，董超

(大连交通大学 机械工程学院，辽宁 大连 116028)



高速列车轴箱圆锥滚子轴承滚动体的对称修形

魏延刚，许凯，董超

(大连交通大学 机械工程学院，辽宁 大连 116028)

基于轴承载荷离散分布计算模型的方法，求出高速列车轴箱圆锥滚子轴承受力最大的滚动体及其所受的最大载荷；采用对数修形曲线进行对称修形，用有限元法对受力最大滚动体进行修形设计的精细研究，在不同工况下分析圆锥滚子与内、外圈之间的最大接触应力沿其母线的分布规律，为高速列车轴箱圆锥滚子轴承的修形优化设计提供了指导.

圆锥滚子轴承；轴承载荷分布；对称修形；有限元；接触应力

0 引言

我国从2004年开始引进高铁技术，到2011年底我国高铁运营里程已经占全世界高铁运营里程的三分之一以上[1].目前我国是世界上具有高速铁路线最长的国家，高速铁路的发展大大地推动了我国的经济发展，促进了人民生活水平的提高.虽然，我国已经能够自主生产高速列车，并且正在向国外出口我国的高速铁路.然而，我们并没完全掌握高速列车全部关键零部件技术，有些关键部件仍需要进口，比如：高速列车轴箱轴承目前仍采用瑞典、德国和日本等国家的轴承.因此，对高速列车轴箱轴承的修形技术进行研究，提高轴承的疲劳寿命具有十分重要的现实意义.

高速列车轴箱轴承是圆锥滚子轴承，那么，圆锥滚子轴承的滚动体修形采用与圆柱滚子轴承的滚动体一样的对称修形方案是否合理，是否应当对两端直径大小不等的圆锥滚子采用非对称修形，采用非对称修形是否是滚动体的大端修量要大于小端的修形量会合理些等等.为了回答这些问题，本文在圆锥滚子轴承对数修形初步研究的基础上[2]，对高速列车轴箱圆锥滚子轴承滚动体的对称修形又进行了深入而又精细的研究，为高速列车轴箱轴承的修形优化方案提供了参考，也为其他圆锥滚子轴承的修形设计提供了有价值的参考.另外，本文有限元模型中的载荷是根据基于轴承载荷离散分布计算模型的方法求得的，比传统的方法所确定的载荷更为精确.

1 基本理论简介

滚动轴承受载后每个滚动体所受的载荷与其所处在位置有关，在不同位置上的滚动体与内、外圈之间的载荷的分布情况就是所谓的滚动轴承载荷分布，滚动轴承的边缘效应与其所受载荷的大小、方向有关，所以，研究滚动轴承的修形一定要求得滚动轴承载荷分布，求出受力最大的滚动体所受的最大力.滚动轴承载荷分布的传统计算方法[3]是将离散的载荷分布

(1)

(2)

用径向积分Jr(ε)和推力积分Ja(ε)的形式来求解，即

(3)

(4)

(5)

(6)

其中载荷分布系数ε为：

(7)

径向积分Jr(ε)和推力积分Ja(ε)与方位角ψ，载荷位移指数n，径向位移δr，轴向位移δa和接触角α相关，由Sjovall H引入的式(4)和式(6)积分是方位角ψ的连续函数[4].是将离散的载荷分布式(1)和式(2)用连续函数式(4)和式(6)来求解，必然会产生一定的误差.本文的滚动轴承载荷分布的求解用的不是这种传统的方法，而是直接用离散的载荷分布式(1)和式(2)，根据滚动体的数目等已知条件，应用数值计算的方法，通过计算机编程求出离散模型的载荷分布，从而更加精确地求出滚动轴承载荷分布.

本文研究的高铁轴箱圆锥滚子轴承的示意图如图1所示，其主要几何参数为：轴承内径130mm，轴承外径240 mm，节圆直径dm=176mm，公称接触角α=8.7295°，滚子数目z=2×17，滚子大径db=28.5 mm，滚子小径ds=26.3 mm，滚子有效长度l=49.6 mm.表1给出了三种工况下，根据离散模型求出的受力最大的滚动体载荷，还给出了滚动体中部与内、外圈之间的最大接触应力及其接触半带宽的赫兹理论解.

图1 轴承基本尺寸图

表1 各工况下的最大滚动体载荷与滚动体中部接触的赫兹理论计算值

最大滚动体载荷/kN最大接触应力/MPa内圈外圈内圈接触半宽/mm外圈接触半宽/mm91048.56905.340.2160.250121207.981042.980.2550.296221657.921431.470.3410.395

2 有限元模型及修形方案效果分析

2.1 有限元模型

由于滚动轴承的疲劳寿命主要取决于其所受的最大应力，所以，根据滚动轴承的载荷分布计算，求出受力最大的滚动体，并以其所受的最大力作为载荷条件，研究滚动体与内外圈的接触情况.圆锥滚子轴承模型由内圈、滚子和外圈组合而成，该模型的接触对有滚子与内、外圈的径向接触，以及滚子大端与挡边的轴向接触.本模型针对的是圆锥滚子轴承的静力学研究，模型装配忽略了轴承的径向游隙影响，以及摩擦因素等影响.

考虑到计算效率和计算容量，根据轴承的接触及承载性能特点，结合接触力学知识，计算出接触对的接触半带宽，根据接触半带宽合理地确定有限元分析模型；为了保证计算精度，在接触对附近区域的网格要足够的细，考虑到计算容量不要太大，在非接触区网格可适当的稀疏些，经过多次调整，并通过滚动体与内、外圈接触区沿滚子轴向中部截面上的最大接触应力的理论解与有限元解的比较(比较结果见表2)，最终确定的有限元分析模型网格图如图2所示.表2说明本文采用有限元分析模型和网格合理，有限元计算精度相当高.

表2 滚动体与内、外圈接触区沿滚子轴向中部截面上的最大接触应力

最大滚动体载荷/kN理论解/MPa有限元解/MPa相对误差/%内圈外圈内圈外圈内圈外圈9104990510338951.531.102216581431161014382.100.49

(a) 有限元模型网络图

(b) 滚子与内、外圈之间的载荷

图2 有限元模型网格图和圆锥滚子轴承滚子与内、外圈之间的载荷

2.2 轻载工况下的计算结果及分析

对滚动体采用公知的最佳修形曲线，对数曲线修形.采取常用的对称修形方案，修形曲线的选取是根据载荷工况不同，用不同的修形曲线方程及不同的凸度量，对不同工况进行了大量的计算分析，为了节省篇幅，在此只给出两种工况下，不修形和7个修形方案的8套计算结果.

最大滚动体载荷为9kN时的轻载工况滚动体与内、外圈的最大接触应力结果如表3所示，图3、4分别是滚子与内、外圈之间的最大接触应力沿滚子母线变化的曲线图.

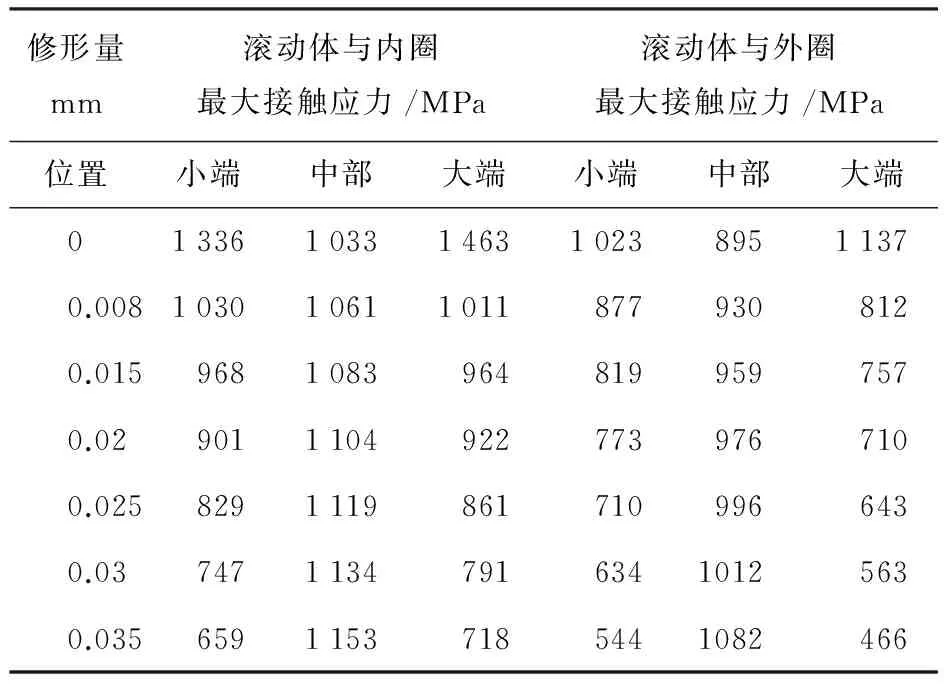
表3 载荷9 kN时接触应力有限元计算结果

滚动体与内圈之间的最大接触应力变化情况分析.根据表3和图3、4可知，不修形时，存在明显的边缘效应，最大接触应力的最小值在滚子中间处，滚子两端的应力远大于中间处的应力，而且是滚子大端处的最大接触应力大于小端处的值.

修形量是0.008时，消除了边缘效应，最大接触应力的最大值出现滚子中间处，且大端的最大接触应力值最小，小端的比大略大点.

图3 轻载时，自滚子小端(左)至大端(右) 滚子与内圈之间的最大接触应力曲线

图4 轻载时，自滚子小端(左)至大端(右) 滚子与外圈之间的最大接触应力曲线

修形0.015时，最大接触应力的变化情况与修形量是0.008时类似，只是中间处的应力值更大，两端的更小；当修形量为0.020～0.035时，最大接触应力的变化情况与修形量0.008～0.015时不同，虽然，最大接触应力的最大值仍然是在滚子中间处，但是，小端的最大应力值小于大端的值.

滚动体与外圈之间的最大接触应力变化情况分析.根据表2和图3、4，首先可知，滚动体与外圈之间的最大接触应力的数值小于滚子与内圈之间接触的数值.不修形时，与滚动体和内圈之间的最大接触应力分布规律相似，存在明显的边缘效应，最大接触应力的最小值在滚子中间处，滚子两端的应力远大于中间处的应力，也是滚子大端处的最大接触应力大于小端处的值.修形时，与滚动体和内圈之间的最大接触应力分布规律有所不同，修形量在0.008～0.035时，都是消除了边缘效应，最大接触应力的最大值出现滚子中间处，且大端的最大接触应力值最小，小端的比大略大些.

2.3 重载工况下的计算结果及分析

重载工况下不同修量时接最大触应力如表4所示，图5、6分别是滚子与内、外圈之间的最大接触应力沿滚子母线变化的曲线图.重载工况下最大接触应力的分布规律与轻载工况下的有一定的差别.

表4 载荷22 kN时接触应力有限元计算结果

滚动体与内圈之间的最大接触应力变化情况分析.根据表3和图5、6可知，不修形时滚动体与内圈之间的最大接触应力变化情况与轻载时类似，存在明显的边缘效应，最大接触应力的最小值在滚子中间处，滚子两端的应力远大于中间处的应力，而且是滚子大端处的最大接触应力大于小端处的值.修形时滚动体与内圈之间的最大接触应力变化情况与轻载时不同.修形量是0.008时，边缘效应仍然存在，滚子与内圈的最大接触应力仍然是两端大于中间的，但小端的最大接触应力值略大于大端的值；修形量是0.015时，滚子与内圈之间的边缘效应没有完全消除，最大接触应力在小端，最小应力在大端：当修形量是0.020～0.035时，完全消除了边缘效应，都是中间的接触力最大，但是大端的最大接触应力值最小，小端的最大接触应力比大端的略大点.而且当修形量是0.035时，滚子与内圈之间的接触应力大端的刚好等于小端的值.

图5 重载时，自滚子小端(左)至大端(右) 滚子与内圈之间的最大接触应力曲线

图6 重载时，自滚子小端(左)至大端(右) 滚子与外圈之间的最大接触应力曲线

滚动体与外圈之间的最大接触应力变化情况分析.不修形时滚动体与外圈之间的最大接触应力变化情况与轻载时不同，小端存在明显的边缘效应，而大端不仅并没有明显的边缘效应，而且最大接触应力的最小值在大端；最大接触应力从小端无边界应集中处到大端滚子近似于斜线分布.修形量是0.008时，边缘效应仍然存在，但最大接触应力的分布规律与不修形时完全相同，只是应力的数值低于不修形时的.当修形量是0.015～0.035时，滚子与外圈的最大接触应力的变化情况与轻载时相似，完全消除了边缘效应，都是中间的接触力最大，大端的接触应力最小，小端的接触应力比大端的略大点.

3 结论

由于滚动体与外圈之间的最大接触应力的数值小于滚动体与内圈之间接触的数值，所以，应当根据滚动体与内圈之间接触应力的变化情况进行修形方案的设计.这样，轻载工况下，修形量小于0.015时，由于滚动体与内圈之间的最大接触应力是小端的应力值大于大端的值，所以，小端的修形量应当大于大端的值；修形量大于0.015时，由于大端的应力值大于小端的值，所以，大端的修形量应当大于小端的值.重载情况下，由于滚动体与内圈之间的最大接触应力都是小端的最大接触应力值大于大端的值，所以，小端的修形量应当大于大端的值.另外，考虑到轻载工况下最佳修形量是0.008 mm，轻载时的修形量没有必要大于0.015mm，因此，无论轻载工况还是重载工况合理的修形方案是小端的修形量大于大端的修形量，也就是说高速列车轴箱圆锥滚子轴承合理的修形方案应该是非对称修形，而且是小端的修形量大于大端的修形量.

本文的研究结果为高速列车轴箱圆锥滚子轴承的修形优化设计提供了指导，有关高速列车轴箱圆锥滚子轴承的非对称修形和修形优化设计的研究将另文进行介绍.

[1]杨晓蔚.高速铁路轴承概述[J].轴承,2011(10)：59-61.

[2]魏延刚，董超.高速列车轴箱圆锥滚子轴承滚子的对数修形[J].大连交通大学学报,2011，32(5)：34-37.

[3]HARRIS T A, KOTZALAS M N. Rolling Bearing Analysis FIFTH EDITION: Essential Concepts of Bearing Technology[M]. [s.l.]: CRC Press,2007.

[4]SJOVALL H. The load distribution within ball and roller bearings under given external radial and axial load[M].[s.l.]: Teknisk Tidskrift Mek, 1933.

Research on Symmetrical Modification of Tapered Roller Bearing of High-Speed Train Journal Box

WEI Yangang, XU Kai, DONG Chao

(School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028, China)

The maximum load and the roller acted by the maximum load of the tapered roller bearing used in High-speed train journal box are calculated through the calculating method based on discrete distribution model of bearing load. Detailed research on symmetrical modification of logarithmic crowned roller is conducted by FEA and the relationship between the crowned quantum of symmetrical logarithmic roller and distribution laws of contact maximum along the profile contact line between the roller, and the races are analyzed under different load cases. The results offer some guides to design the optimum modification.

tapered roller bearing; bearing load distribution; symmetrical modification; finite element; contact stress

1673- 9590(2016)03- 0044- 05

2015-07-15

魏延刚(1961-)，男，教授，硕士，主要从事机械传动的研究E- mail:ygwang78@126.com.

A