Characterization of bipartite graph With maximum spectral radius
2016-11-28NIUAihongWANGGuopingQINZhengxinMUShanzhi
NIU Ai-hong,WANG Guo-ping,QIN Zheng-xin, MU Shan-zhi
(1.School of Mathematical Sciences,Xinjiang Normal University, Urumqi 830054,China; 2.College of Mathematics and System Sciences,Xinjiang University, Urumqi 830046,China; 3.Department of Mathematics,Jiangsu University of Technology, Changzhou Jiangsu 213001,China)
Characterization of bipartite graph With maximum spectral radius
NIU Ai-hong1,WANG Guo-ping1,QIN Zheng-xin2, MU Shan-zhi3
(1.School of Mathematical Sciences,Xinjiang Normal University, Urumqi 830054,China; 2.College of Mathematics and System Sciences,Xinjiang University, Urumqi 830046,China; 3.Department of Mathematics,Jiangsu University of Technology, Changzhou Jiangsu 213001,China)
The adjacency matrix A(G)of a graph G is the n×n matrix With its(i,j)-entry equal to 1 if viand vjare adjacent,and 0 otherwise.The spectral radius of G is the largest eigenvalue of A(G).In this paper we determine the graphs With maximum spectral radius among all trees,and all bipartite unicyclic,bicyclic,tricyclic,tetracyclic,pentacyclic and quasi-tree graphs,respectively.
bipartite graph;cycle;spectral radius
0 Introduction
Let G be a connected simple graph With Vertex set V(G)={v1,v2,···,vn}.The adjacency matrix of G,denoted by A(G),is the n×n matrix With its(i,j)-entry equal to 1 if viand vjare adjacent,and 0 otherwise.The spectral radius of G is the largest eigenvalue of A(G). The spectral radius of a connected graph has been studied extensively(see[1-4]).Zhai,Liu and Shu[5]characterized the bipartite graphs With given diameter which attain the maximum and the second largest spectral radius,respectively.Nath and Paul[6]determined the graphs With minimum distance spectral radius among all connected bipartite graphs of order n With a given matching number and Vertex connectivity.Zhang and Zhang[7]obtained the graphs With maximum Laplacian spectral radius among all bipartite graphs With k cut-edges,and among all bipartite bicyclic graphs,respectively.Li,Shiu and Chan[8]gaVe the graphs With maximum Laplacian spectral radius among all bipartite graphs with(edge-)connectivity at most k.
Li,Shiu and Chan[9]determined the graphs with maximum Laplacian spectral radii among all trees,and all bipartite unicyclic,bicyclic,tricyclic and quasi-treegraphs,respectively.In this paper we determine the graphs with maximum spectral radius among all trees,and all bipartite unicyclic,bicyclic,tricyclic,tetracyclic,pentacyclic and quasi-tree graphs,respectively.
1 Extremal bipartite graphs
For each v∈V(G),let NG(v)(or N(v)for short)be the set of Vertices which are adjacent to v in G.
Lemma 1.1[10]Let u and v be two vertices oƒ a connected graph G,and suppose that v1,v2,···,vs∈N(v)N(u).Let G*be the graph obtained ƒrom G by deleting the edges vviand adding the edges uvi(1≤i≤s).Let x be the Perron vector oƒG corresponding toρ(G).Iƒ x(u)≥x(v),thenρ(G*)>ρ(G).
Let G be a bipartite graph With bipartition(X,Y).If X=X1∪X2∪···∪Xhand Y=Y1∪Y2∪···∪Yhsatisfy Xiand Yiare not em pty,and the neighborhood of each Vertex in Xiis Y1∪Y2∪···∪Yh+1-i(1≤i≤h),then we call G double nested graph as in[9].If |Xi|=aiand|Yi|=bi(i=1,2,···,h),then G is denoted by D(a1,a2,···,ah;b1,b2,···,bh).
Theorem 1.2 IƒG=(X,Y)attains the maximum spectral radius among all bipartite graphs,then G is a double nested graph with all pendant edges attached at a vertex.
P roo f Let X={v1,v2,···,vj}and Y={vj+1,vj+2,···,vn}such that x(v1)≥x(v2)≥···≥x(vj)>0 and x(vj+1)≥x(vj+2)≥···≥x(vn)>0.Then we have the following three claim s.
贵州魂:这是对贵州独有的古生物化石的赞谓,虽已超出色彩的范围,却是贵州观赏石资源中的特色品种,是贵州具有独特性和唯一性的观赏石资源,具有古生物生命演化的神韵,是许多博物馆争相收购的镇馆之宝。贵州省古生物化石资源丰富,但急需加强保护和有效进行开发利用。
Claim 1 A ll cut-edges in G are pendant edges and are attached at a common Vertex.
If it is not so,then,by Lemma 1.1,we can obtain the other bipartite graph H such that ρ(H)>ρ(G),which contradicts maximality of G.
C laim 2 N(v1)⊇N(v2)⊇···⊇N(vj)and N(vj+1)⊇N(vj+2)⊇···⊇N(vn). MoreoVer,for some l,N(vl)=N(vl+1)if and only if x(vl)=x(vl+1).
The Claim 2 is clearly true from Lemma 1.1.
Claim 3 G is a double nested graph.
Without loss of generality we assume that x(v1)≥x(vj+1).Suppose that a1>a2>···>ahare all distinct real numbers among{x(v1),x(v2),···,x(vj)}.Let Xk={vi∈X|x(vi)=ak} (1≤k≤h).Then X=X1∪X2∪···∪Xh.The Claim 2 shows that Y=Y1∪Y2∪···∪Yh.
Up to now the proof is completed.
2 Extremal bipartite graphs With at most five cycles
If a graph on n Vertices is of n+k-1 size then it is called k cycles graph.In this section we assume that G=(X,Y)is an k cycles bipartite graph on n Vertices With the maximum spectral radius.Next we exactly characterize G when k∈{0,1,2,3,4,5}.
Theorem 2.1[11]W hen k=0,GSn,where Snis a star with order n.
It is clear that n≥k+3 when k≥1.
P roo f From Theorem 1.2 we can see that there is a partition,say X,such that for each v∈X,d(v)≥2,which im p lies that|X|=2.This shows that the result is true.
Lemma 2.3[12],whereΔ(H)is the maximum degree oƒH.
Now we giVe the characterization of G when k=2,3,4,5.
We only Verify Theorem 2.6 and other theorem s can be similarly proVed.
P roof of Theorem 2.6 From Theorem 1.2 we can see that there is a partition,say X,such that for each v∈X,d(v)≥2,which im p lies that|X|=2,3,4 or 5.In this case, we can easily know that G is isomorphic to some one of D(2;5),D(1,2;3,1)and D(2,1;2,2)if n=7,and that G is isomorphic to some one of D(1,1;5,n-7),D(1,2;3,n-6),D(1,1,1;2,2,n-7),D(1,1,2;2,1,n-7)and D(1,4;2,n-7)if n≥8.By calculation we obtain thatThus,when n=7,GD(2;5).Next we assume n≥8.
Let H0=D(1,1;5,n-7),H1=D(1,2;3,n-6),H2=D(1,1,1;2,2,n-7),H3= D(1,1,2;2,1,n-7)and H4=D(1,4;2,n-7)be shown in Fig.1.
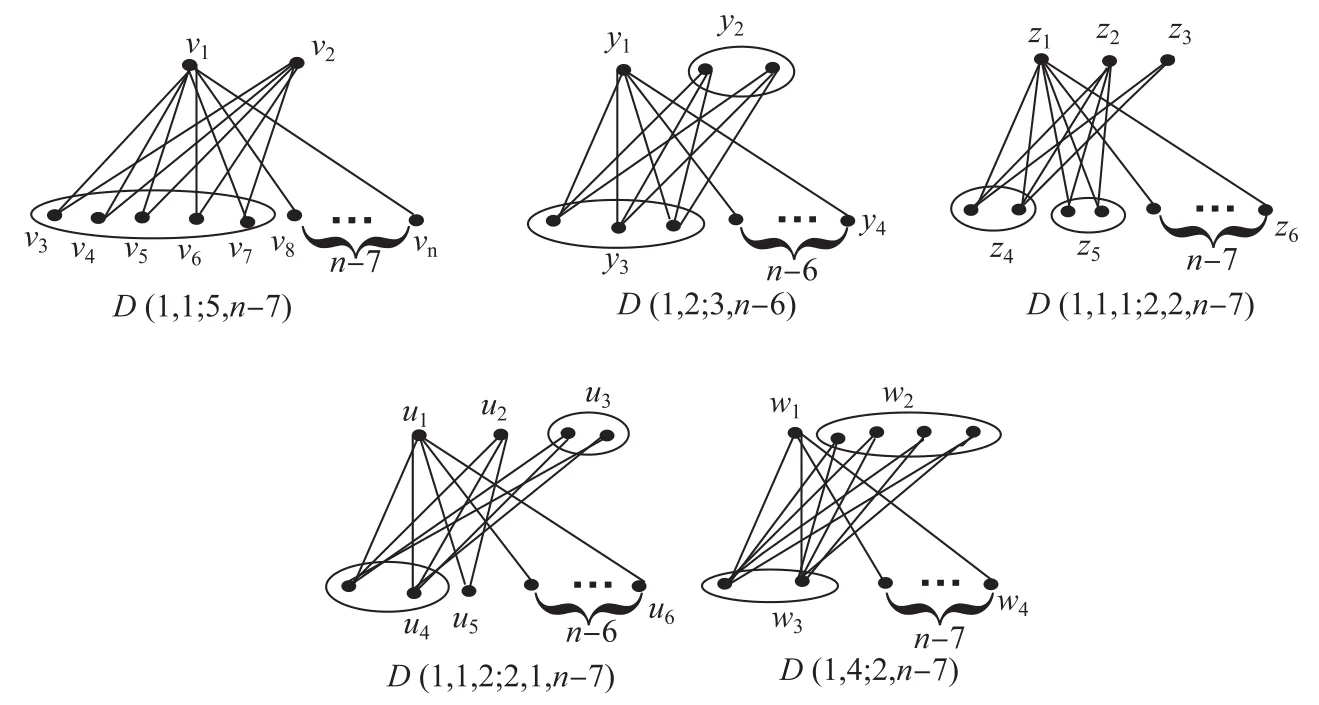
Fig.1 H i(i=0,1,2,3,4)
Set x to be the Perron Vector of H0.By symmetry,we can set x(v3)=···=x(v7)=x3and x(v8)=···=x(vn)=x4.Let x(v1)=x1and x(v2)=x2.Then


3 Extremal bipartite quasi-tree graphs
If there exists u0∈V(G)such that G-u0is a tree,then we call G quasi-tree graph as in[9].LetΨ(n,d0)={G|G is a bipartite graph of order n With G-u0is a tree and d(u0)=d0}. Clearly,Ψ(n,1)is the set of trees of order n,and Theorem 2.1 shows that Snattains the maximum spectral radius am ong all trees.
Theorem 3.1.Let 2≤d0≤n-2 and suppose that H∈Ψ(n,d0)attains the maximum spectral radius.Then HD(1,1;d0,n-d0-2).
P roof Let H=(X,Y).From Theorem 1.2 we can see that there is a partition,say X, such that for each v∈X,d(v)≥2.Thus,|X|=2 if u0∈X,and|X|=d0if u0∈Y.In this case,we can easily know that HD(1,1;d0,n-d0-2)or HD(1,d0-1;2,n-d0-2).
W hen d0=2,HD(1,1;2,n-4),and when d0=n-2,HD(2;n-2).
Next we assume that 3≤d0≤n-3.
Let H*=D(1,1;d0,n-d0-2)and e H=D(1,d0-1;2,n-d0-2)be shown in Fig.2.
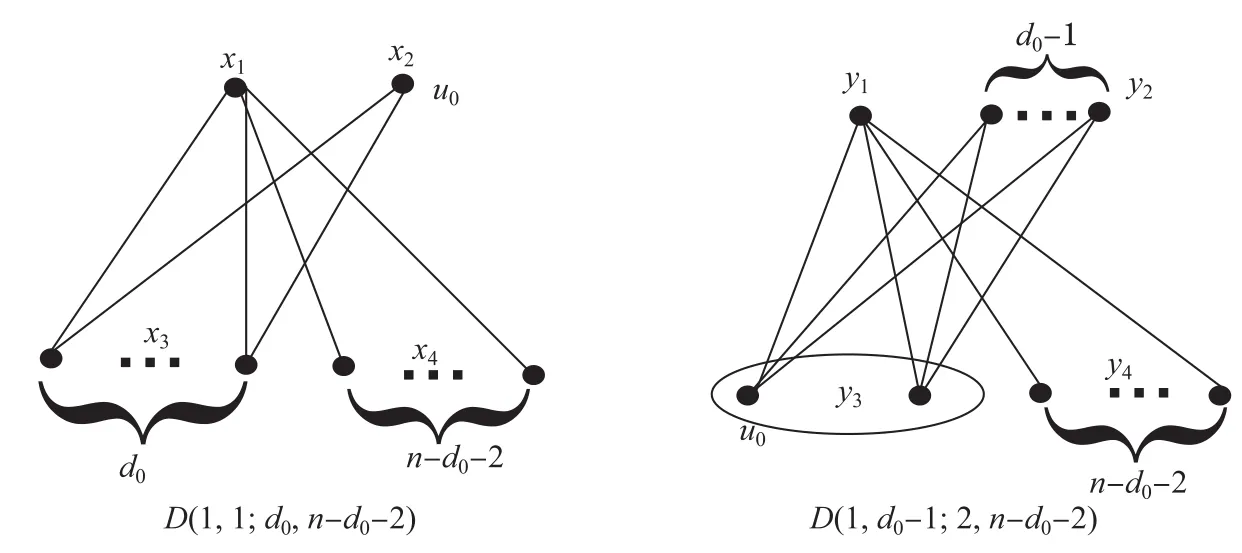
Fig.2 H*and

[1]BERMAN A, ZHANG X D. On the spectral radius of graph with cut vertices [J]. J Combin Theory Ser B, 2001,83: 233-240.
[2]BRUALDI R, SOLHEID E. On the spectral radius of connected graphs [J]. publ Inst Math (Beograd), 1986, 39(53): 45-53.
[3]HOU Y p, LI J S. Bounds on the largest eigenvalues of trees with a given size of matching [J]. Linear Algebra Appl, 2002, 342: 203-217.[4] LIU H Q,LU M,TIAN W F.On the spectral radius of graphs with cut edges[J].Linear Algebra Appl,2004, 389:139-145.
[5] ZHAI M Q,LIU R F,SHU J L.On the spectral radius of bipartite graphs with given diameter[J].Linear Algebra Appl,2009,430:1165-1170.
[6] NATH M,PAUL S.On the distance spectral radius of bipartite graphs[J].Linear Algebra Appl,2012,436: 1285-1296.
[7] ZHANG X L,ZHANG H P.The Laplacian spectral radius of some bipartite graphs[J].Linear Algebra Appl, 2008,428:1610-1619.
[8] LI J X,SHIU W C,CHAN W H.The Laplacian spectral radii of some graphs[J].Linear Algebra Appl,2009, 431:99-103.
[9] LI J X,SHIU W C,CHAN W H.On the Laplacian spectral radii of bipartite graphs[J].Linear Algebra Appl, 2011,435:2183-2192.
[10] WU B F,XIAO E L,HONG Y.The spectral radius of trees on k pendent vertices[J].Linear Algebra Appl, 2005,395:343-349.
[11] NEUMAIER A.The second largest eigenvalue of a tree[J].Linear Algebra Appl,1982,46:9-25.
[12] CVETKOVIC D M,DOOB M,SACHS H.Spectra of graphs:Theory and application[J].Math Hungar,1995, 6(2):191-195.
(责任编辑 李 艺)
具有最大谱半径的二部图的刻画
牛爱红1,王国平1,秦正新2,牟善志3
(1.新疆师范大学数学科学学院,乌鲁木齐830054; 2.新疆大学数学与系统科学学院,乌鲁木齐830046; 3.江苏理工学院数学系,江苏常州213001)
一个图G的邻接矩阵A(G)是n×n矩阵,如果vi和vj相邻,那么它的(i,j)位置为1,否则为0.图G的谱半径是邻接矩阵A(G)的最大特征值.本文确定了在所有的树和所有的二部单圈图、二部双圈图、二部三圈图、二部四圈图、二部五圈图以及二部拟树图中所对应的具有最大谱半径的图.
二部图;圈;谱半径
2015-01
国家自然科学基金(11461071)
牛爱红,女,硕士研究生,研究方向为图论.E-mail:949751277@qq.com.
王国平,男,教授,研究方向为图论.E-mail:x j.wgp@163.com.
O 157.5 Document code:A
10.3969/j.issn.1000-5641.2016.01.012
1000-5641(2016)01-0096-06
