概化理论G研究方差分量及其变异量估计影响因素*
2016-11-26黎光明
黎光明
(1.华南师范大学心理学院,心理应用研究中心,广州 510631;2.心理健康与认知科学广东省重点实验室,广州 510631)
概化理论G研究方差分量及其变异量估计影响因素*
黎光明1,2
(1.华南师范大学心理学院,心理应用研究中心,广州 510631;2.心理健康与认知科学广东省重点实验室,广州 510631)
概化理论是关于行为测量可靠性的统计理论。G研究是进行概化理论分析的关键步骤,其主要目的是进行方差分量及其变异量估计。总结了影响概化理论G研究方差分量及其变异量估计的多种因素,包括估计方法、数据分布、研究设计、样本容量、模型效应和数据形态等,并指出了相关研究存在的六方面不足,如缺乏估计方法的综合比较、较少考察非正态分布数据、较少考虑不平衡或缺失数据等。
概化理论;G研究;方差分量;方差分量变异量估计
1 概化理论
概化理论(Generalizability Theory,GT)是关于行为测量可靠性(dependability)的统计理论(Shavelson & Webb,1991,p.1)。Cronbach,Gleser,Nanda和Rajartnam(1972,p.15)构建了可靠性的概念:来自于一次测验或其它测量用作决策的分数,仅仅是许多分数中的一个,这些分数可能起着相同目的,决策者从来不对在特定刺激物、问题、测验者、测验时间等条件下产生的(这些)分数感兴趣,因为一些测验条件容易改变,而用于决策的理想分数是包含所有条件下获得的观察分数。根据Cronbach等人构建的可靠性概念,可靠性被定义为:将一次测量(如心理测验、行为观察、民意调查等)所得的观察分数概化到包含所有可能条件下平均分的精确度,这些可能的条件是测验者愿意接受的。可靠性概念的前提假设是人的知识、态度、技能等都处于稳定状态,仅仅是不同来源的误差造成了个体之间的分数差异。
概化理论可用于分析多侧面测量误差(multifaceted measurement error),将测量的情境关系(context of measurement situation)分为测量目标和测量侧面两部分(Shavelson & Webb,1991)。测量目标(object of measurement)是欲考察的实际特质,而测量侧面(facet of measurement)是影响测量目标的各种因素。根据测量的情境关系,在测量目标确定的条件下,测量侧面可以来自多方面,例如,学生评价教师教学水平,测量目标是教师教学水平,测量侧面可以是学生、班级、专业、课程、项目以及教学水平维度(如教学态度、教学内容、教学方法、教学效果等)(Meyer,Liu,& Mashburn,2014;Casabianca,Lockwood,& McCaffrey,2015)。针对某个测量目标,如果测量侧面仅一个,称之为单侧面设计,如p×i设计。对于p×i设计,如果i为随机侧面,可称为单侧面随机设计,相应地,如果i为固定侧面,可称为单侧面固定设计。如果测量侧面超过一个,称之为多侧面设计,设计类型可以是交叉、嵌套,也可以是混合。
概化理论也可以分析多个测量目标与测量侧面的情境关系,这就是多元概化理论(Multivariate Generalizability Theory,MGT)(Brennan,2001)。MGT是在单变量概化理论(Univariate Generalizability Theory,UGT)的基础上发展起来的。MGT是UGT的深化和发展。与UGT一样,MGT同时吸收了经典测量理论、实验设计和方差分析的思想。
2 概化理论G研究
2.1 概化理论G研究方差分量估计
进行GT分析主要包括G研究和D研究两个过程,G研究是概化研究,D研究是决策研究。G研究的主要任务是在观测全域(universe of admissible observations)上尽可能地“挖掘”出研究设计中各种潜在的测量误差来源,并估计这些误差来源的方差分量(variance component)。D研究的主要任务是在概化全域(universe of generalizability)上,为了某种特殊的决策需要,以G研究所得到的方差分量估计值为基础,通过调整测量过程中的各种关系(如调整各个侧面样本水平数、调整各个侧面之间的关系或权重等),来探索如何控制和调节测量误差。G研究是D研究的基础,D研究是G研究的深化。从G研究和D研究分析过程看,方差分量估计是进行概化理论分析的关键,这是因为,要得到D研究的相关统计量,如信噪比(S/N)、概化系数(Eρ2)、可靠性指数(φ)等都依赖于G研究所估出的方差分量。方差分量估计是概化理论的必用技术,是进行概化理论分析的关键。概化理论借用实验设计与方差分析技术,对心理与教育测量中产生的总变异进行分解。测量侧面在多大程度上影响了测量目标,即在总变异中,测量目标和测量侧面的方差分量各占多少,是概化理论分析关心的问题。因此,需要探测测量侧面在多大程度上影响到测量目标,并对其产生的误差进行有效控制。
结合测量的情境关系,概化理论对经典测量理论给出的笼统误差进行探查和分解,辨明误差的不同来源,并且在一定范围内变动测量的情境关系,以考察这种变动引起的误差的相对变化,从而达到对误差方差进行控制(Shavelson & Webb,1991)。因此,概化理论又称为方差分量模型(variance component model)(Brennan,2000)。
2.2 概化理论G研究方差分量变异量估计
与其它统计量一样,概化理论下估计出的方差分量受限于抽样,不同的抽样样本,所估计的方差分量可能不一样,这就要求进行方差分量估计时需要对其变异量进行探讨。一般地,仅根据一个样本的统计量来估计总体参数,可能存在偏差。在样本统计量研究中,仅用一个(次)样本平均数来估计总体均值,存在较大的风险,因为样本平均数容易受抽样的影响。探讨方差分量变异量具有重要意义,这是因为,报告这些变异量可以在一定程度上说明方差分量测量的可靠性。概化理论G研究方差分量变异量主要包括标准误和置信区间估计(Brennan,2001;Shin & Raudenbush,2012)。
3 概化理论G研究方差分量及其变异量估计影响因素
进行概化理论G研究方差分量及其变异量估计,需要考虑较多条件(影响因素),如估计方法、数据分布、研究设计、样本容量、模型效应及数据形态等。
3.1 估计方法
《教育与心理测试标准》(Standards for Educational and Psychological Testing,AERA,APA,& NCME,1999,p.27)和Brennan(2001,p.180)指出,为了获得准确的方差分量变异量,理想的做法是进行多次独立的重复测量。Brennan(2001,p.181)对9个ACT数学平行测验进行了方差分量及其标准误估计,结果如表1所示。
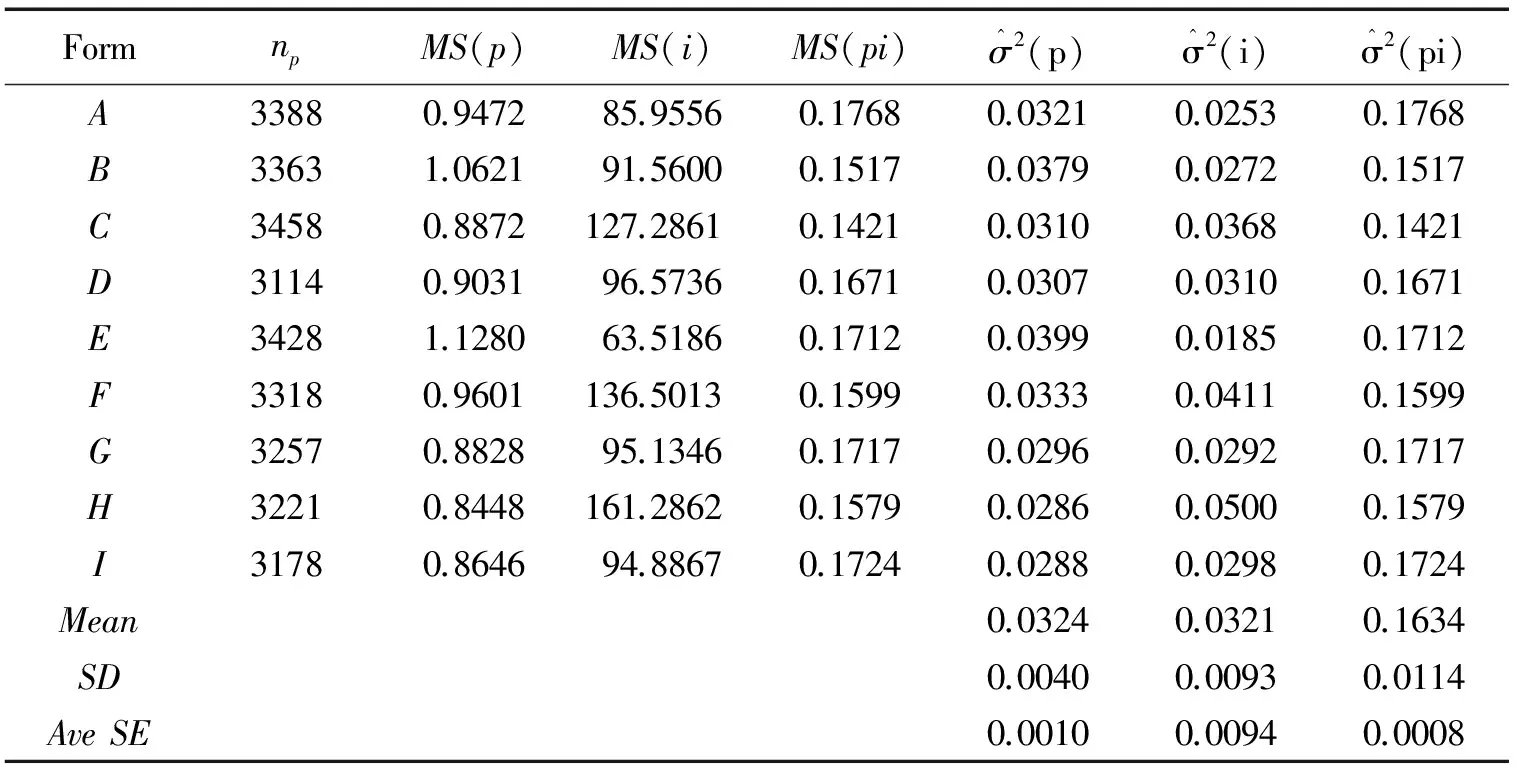
表1 九个ACT数学平行测验估计的方差分量及其标准误
3.2 数据分布
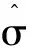
不同数据分布下不同方法对方差分量变异量估计可能产生不同的影响。特别地,当数据为非正态分布时,如二项分布、多项分布和偏态分布,适合于正态分布数据的方差分量变异量估计方法不一定适合于非正态分布数据。因此,也需要探讨和比较基于不同非正态分布数据下不同方差分量变异量估计方法的优劣。非正态分布数据在心理与教育测量实践中具有常见性。例如,一些考试中的选择题、是非题等,仅有两种分数(错和对):0和1,就是二项分布数据。又如,一些心理与教育测验中的等级评分,具有多个数据点,存在多种分数,如0~4分,则表示分数可取五个点,分别是0、1、2、3和4分,就是多项分布数据。而对于偏态分布数据,在实践中也具有常见性,这是因为随着社会的发展,心理与教育测量的应用领域发生了较大变化,被测群体的知识和能力等特质在一定程度上不再服从偏度为0的分布。
3.3 研究设计
常见的概化理论研究设计包括p×i、i:p、p×i×r、p×(i:r)、i:(p×r)、i:p:r等。其中对概化理论单侧面随机p×i设计研究最多,这种设计属于单变量概化理论的交叉设计,p为测量目标,i为测量侧面,p和i都随机,p和i具有交叉关系(Brennan,2001,p.5)。
但是,随着研究设计侧面数和复杂度的增加,G研究难度加大。Smith(1981)指出,概化理论G研究方差分量估计的稳定性受研究设计复杂度(侧面数)和研究设计构成(设计中嵌套的程度)影响。Smith认为使用多侧面(multiple)设计所得方差分量的方差更小,因为用来估计方差分量方差的均方在多侧面设计中比在单个复杂(singlecomprehensive)设计中要小。例如,学生(p)嵌套在学校(s)中,施测若干个项目(i),项目嵌套在测验(f)中,那么这个设计可表达成(p:s)×(i:f)。这个设计是多侧面复杂设计,来自于每个学校的学生都被施测每个测验的项目。对于(p:s)×(i:f),还有可供替代的单个复杂设计,如p:[s×(i:f)]和i:[f×(p:s)],前者表示每个学校不同组的学生被施测不同测验的每个项目(也就是说,对于每个学校的学生有“学生-项目”形式),后者表示对于每个学校每个测验的项目施测于一个学生样本(也就是说,对于每个测验的项目有“项目-学生”形式)。与(p:s)×(i:f)设计相比,p:[s×(i:f)]设计和i:[f×(p:s)]设计估计的方差分量均方更大,所以产生的误差也更大。虽然p:[s×(i:f)]和i:[f×(p:s)]设计也可以将所有的方差分量都估计出来,但Smith指出,多侧面设计与单个复杂设计相比,G研究估计的方差分量更为稳定,前者通常使用随机观察数,而后者通常使用固定观察数。
3.4 样本容量
样本容量对G研究方差分量及其变异量估计有影响。Cronbach,Gleser,Nanda和Rajaratnam(1972)认识到教育和社会背景中准确估计方差分量对决策的重要性,认为研究者利用小样本数据估计G研究方差分量,有时是站不住脚的,需要考察方差分量的变异量。Gao和Brennan(2001)认为,估计的方差分量因不同样本存在差别,特别是当样本较小时这种差异更加明显,准确估计方差分量对于解释评价结果至关重要,在其它条件相等的情况下,大样本有助于获得更为准确的估计结果,因为大样本所估计的标准误更小。
对于一个p×i设计,样本容量可以是30×5、30×20、600×5、600×20等,p和i因素可能存在“样本水平不一致性”(disproportionality),表示一个因素的样本容量与另一个因素的样本容量不相一致。“样本水平不一致性”在表现性评价中比较普遍,因为表现性评价经常是较多的人作答较少的题目,即人多题少(Othman,1995)。“样本水平不一致性”对G研究方差分量及其变异量估计有影响。Brennan,Harris和Hanson(1987)的研究表明,“样本水平不一致性”较大时,Satterthwaite方法估计G研究方差分量置信区间不理想。Leucht和Smith(1989)认为,“样本水平不一致性”存在时,使用水平数较大者作为Bootstrap再抽样策略,更为合理,如人的样本容量超过了题目的样本容量,那么再抽样人,采用boot-p策略,反之,采用boot-i策略。Othman(1995)研究发现,“样本水平不一致性”对Satterthwaite、TBGJL和Bootstrap方法估计正态分布数据和二项分布数据方差分量及其变异量有影响,“样本水平不一致性”越大,这种影响越大。
3.5 模型效应
概化理论模型可以分为随机效应模型、固定效应模型和混合效应模型三种(Brennan,2001;Chien,2008)。随机效应模型是最常见的一种,假定测量目标和测量侧面都是随机,即样本来自于一个较大容量总体,且是随机抽取出来的。例如,对于一个样本容量20×8的随机效应p×i设计,测量目标是学生(p),测量侧面是项目(i),p和i都随机,构成测量的情境关系。测量目标对应的总体是测量总体(populationofmeasurement),假定为无限,那么这20个人表示是从一个无限学生总体中随机抽样出来的。测量侧面对应的总体是测量全域(universeofmeasurement),假定为无限,那么这8个题目是从一个无限题目全域中随机抽样出来的。
判断概化理论模型属于随机效应模型,测量侧面必须满足下列三个条件(Shavelson&Webb,1991,p.11):一是当样本的大小比全域要小得多;二是样本被认为是随机抽取的;三是所抽取的样本与从同一全域抽出另外的样本是可以相互交换。如果这些条件难以满足,那么测量侧面是固定侧面,概化理论模型则属于固定效应模型。如果这些条件部分得到满足,既有随机侧面又有固定侧面,那么概化理论模型则属于混合效应模型。Brennan(2001,pp.86-94)对三种模型效应的G研究方差分量估计进行了介绍。不同的模型效应对G研究方差分量及其变异量估计有影响。Brennan,Harris和Hanson(1987)认为,G研究方差分量估计应该考虑总体是来自于有限总体还是无限总体,全域是来自于有限全域还是无限全域。Mislevy(2001)运用MCMC方法同时估计随机效应模型和固定效应模型G研究方差分量变异量,对所得结果进行比较,发现不同的模型效应对G研究方差分量变异量估计也有影响。
3.6 数据形态
这里,数据形态是指平衡与不平衡、有缺失与无缺失等形态。在概化理论中,缺失数据(sparsedata)属于不平衡数据(unbalanceddata)的一种特殊情况(Chiu&Wolfe,2002)。
概化理论平衡设计方差分量估计多采用ANOVA方法或T方法(Tterms),不平衡设计多采用类似ANOVA方法(AnalogousANOVA)或类似T方法(AnalogousTterms)。概化理论平衡与不平衡数据方差分量估计方法(Brennan,2001),如表2所示。

表2 概化理论平衡与不平衡数据方差分量估计方法
缺失数据是相对于完整(无缺失)数据而言的,缺失的原因可能是多方面的,如测评时的遗漏等。对于缺失数据G研究方差分量估计,Brennan(2001)提出了估计概化理论缺失数据方差分量的公式,针对单侧面交叉设计,在数据少量缺失的情况下可以得出方差分量的无偏估计。Chiu 和Wolfe(2002)认为,也可以采用MBIB方法(Modified Balanced Incomplete Block)估计概化理论缺失数据方差分量。
4 问题与展望
概化理论G研究,是进行概化理论分析关键的一步,G研究是D研究的基础,主要任务是进行方差分量及其变异量估计。G研究方差分量估计和方差分量变异量估计受到许多因素影响。当前,对于概化理论G研究方差分量及其变异量估计影响因素,一些研究进行过探讨,但存在以下不足:
第一,缺乏估计方法的综合比较。多数研究仅限于一种或两种估计方法,缺少将Traditional、Bootstrap、Jackknife和MCMC四种方法一同比较的研究,特别是有关MCMC方法估计概化理论方差分量及其变异量方面的研究较少,这就导致了所得结果仅是“片断”方法的研究结果,无法进行方法的综合比较,所得结果在不同数据分布下也缺乏进一步的推广性。
第二,较少考察非正态分布数据。一些研究所考虑的非正态分布数据也仅限于二项分布数据或多项分布数据,缺少对偏态分布数据进行探讨,虽然Othman(1995)已经考虑到数据分布具有(弱)偏态,但是并没有进行偏态分布数据方差分量及其变异量估计的研究,显得不足。
第三,对多侧面设计关注不足。关注单侧面设计的研究居多,对多侧面设计关注不足。测量目标可能受到多个因素影响,仅关注一个测量侧面,存在局限。关注多侧面设计是一种趋势,因为随着测量侧面数的增加,能够分解出更多的方差分量,有助于增强测量控制误差的能力。
第四,抽取的样本不具代表性。概化理论是随机抽样理论(漆书青,戴海崎,丁树良,2002),要求测量的数据具有代表性,样本过少,将导致估计的方差分量不稳定。另外,也有一些研究缺少考察“样本水平不一致性”,往往仅考察一种样本水平,如100×20,这将导致所得的结论难以拓广至其它样本情形。
第五,使用随机效应模型居多。特别地,对于G研究方差分量变异量估计,较少学者真正意义上探讨过固定效应模型和混合效应模型。根据Mislevy(2001)建议,可以使用MCMC方法估计固定效应模型和混合效应模型G研究的方差分量及其变异量。
第六,较少考虑不平衡或缺失数据。大多数研究设计仅考虑平衡设计,较少考虑不平衡设计,而这种设计在实践中经常存在。鲜有学者用MCMC方法估计过缺少数据的方差分量及其变异量,实际上MCMC方法通过运用Bayes先验分布,可以对“缺失”数据进行有效处理,避免了舍弃部分数据丢失大量信息的尴尬局面。
漆书青,戴海崎,丁树良.(2002).现代教育与心理测量学原理(pp.42-78).北京:高等教育出版社.
American Educational Research Association,American Psychological Association,National Council on Measurement in Education.(1999).Standardsforeducationalandpsychologicaltesting(Rev.ed.).Washington,DC:Author.
Brennan,R.L.,Harris,D.J.,& Hanson,B.A.(1987).Thebootstrapandotherproceduresforexaminingthevariabilityofestimatedvariancecomponentsintestingcontexts(ACT Research Report Series87-7).Iowa City,IA:American College Testing Program.
Brennan,R.L.(2000).(Mis)conceptions about generalizability theory.EducationalMeasurement:IssuesandPractice,19(1),5-10.
Brennan,R.L.(2001).Generalizabilitytheory.New York:Springer-Verlag.
Briggs,D.C.,& Wilson,M.(2007).Generalizability in item response modeling.JournalofEducationalMeasurement,44(2),131-155.
Casabianca,J.M.,Lockwood,J.R.,& McCaffrey,D.F.(2015).Trends in classroom observation scores.EducationalandPsychologicalMeasurement,75(2),311-337.
Chien,Y.M.(2008).Aninvestigationoftestlet-baseditemresponsemodelswitharandomfacetsdesigningeneralizabilitytheory.Unpublished doctoral dissertation.University of Iowa.
Chiu,C.W.T.,& Wolfe,E.W.(2002).A method for analyzing sparse data matrices in the generalizability theory framework.AppliedPsychologicalMeasurement,26(3),321-338.
Cronbach,L.J.,Gleser,G.C.,Nanda,H.,& Rajaratnam,N.(1972).Thedependabilityofbehavioralmeasurements:Theoryofgeneralizabilityforscoresandprofiles.New York:Wiley.
Feng,W.C.(2002).ApplicabilityofthejackknifeprocedureforestimatingstandarderrorsofvariancecomponentestimatesinselectedrandomeffectsGstudydesigns.Unpublished doctoral dissertation.University of Iowa.
Gao,X.H.,& Brennan,R.L.(2001).Variability of estimated variance components and related statistics in a performance assessment.AppliedMeasurementinEducation,14(2),191-203.
Leucht,R.M.,& Smith,P.L.(1989).Theeffectsofbootstrappingstrategiesontheestimationofvariancecomponents.Paper presented at the annual meeting of the American Educational Research Association,San Francisco,CA.
Li,F.F.(2009).Aninformationcorrectionmethodfortestlet-basedtestanalysis:Fromtheperspectivesofitemresponsetheoryandgeneralizabilitytheory.Unpublished doctoral dissertation.University of Maryland.
Mao,X.,Shin,D.,& Brennan,R.L.(2005).EstimatingthevariabilityofestimatedvariancecomponentsandrelatedstatisticsusingtheMCMCprocedure:Anexploratorystudy.Paper presented at the annual meeting of the National Council on Measurement in Education,Montreal.
Meyer,J.P.,Liu,X.,& Mashburn,A.J.(2014).A practical solution to optimizing the reliability of teaching observation measures under budget constraints.EducationalandPsychologicalMeasurement,74(2),280-291.
Mislevy,R.J.(2001).Generalizabilitytheory:AbriefintroductiontoBayesianinferenceing-theory.Available from http://www.education.umd.edu/EDMS
Othman,A.R.(1995).Examiningtasksamplingvariabilityinscienceperformanceassessments.Unpublished doctoral dissertation.University of California,Santa Barbara.
Shavelson,R.J.,& Webb,N.M.(1991).Generalizabilitytheory:Aprimer.Newbury Park,CA:Sage.
Shin,Y.,& Raudenbush,S.W.(2012).Confidence bounds and power for the reliability of observational measures on the quality of a social setting.Psychometrika,77(3),543-560.
Smith,P.L.(1981).Gaining accurancey in generalizability theory:Using mulitiple designs.JournalofEducationalMeasurement,18,147-154.
Tong,Y.,& Brennan,R.L.(2007).Bootstrap estimates of standard errors in generalizability theory.EducationalandPsychologicalMeasurement,67(5),804-817.
Influence Factors of Estimating of Variance Components and Their Variability for Generalizability Study in Generalizability Theory
Li Guangming1,2
(1.School of Psychology,Center for Studies of Psychological Application,South China Normal University,Guangzhou 510631;2.Key Lab of Mental Health and Cognitive Science of Guangdong Province,Guangzhou 510631)
Generalizability theory is a statistical theory about the dependability of behavioral measurements.Generalizability studies,which focus on estimating the variance components and the variability of estimated variance components,is a crucial step of performing the generalizability analyses for generalizability theory.Estimation of variance components and their variability for generalizability study was influenced by some factors such as estimation procedure,data distribution,research design,sample size,model effect and data mode and so on.There was some deficiency in some researches about the influence factors for generalizability study such as lack of synthetic research about estimation procedures,less researches about non-normal data distribution,little focus on multifaceted design,only using random effect model,relatively less researches of unbalanced and sparse data.
Generalizability theory;Generalizability study;Variance component;Estimating the variability of estimated variance components
2014年国家自然科学基金面上项目(31470050),广州市教育科学“十二五”规划2012年度面上一般课题(12AO19),广州市教育科学“十二五”规划2014年重大课题(1201411413),广东省2015年度高等教育改革项目(粤教高函[2015]173号),华南师范大学2014年度校级高等教育教学研究和改革项目(教学[2014]52号)。
黎光明,E-mail:Lgm2004100@sina.com。
B841.2
A
1003-5184(2016)05-0458-06
