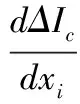收入不平等测度方法选择研究与基于中国数据的检验*
2016-11-26龚志民熊唯伊
龚志民,熊唯伊
(湘潭大学 商学院,湖南 湘潭 411105)
收入不平等测度方法选择研究与基于中国数据的检验*
龚志民,熊唯伊
(湘潭大学 商学院,湖南 湘潭 411105)
从规范和实证的角度,证明了赛尔第二测度是比基尼系数和赛尔测度等其他测度更优良的不平等测度。理论分析和模拟实验均表明,赛尔第二测度对贫困人口的收入变动有恰当的敏感性。相对于基尼系数等其他测度,赛尔第二测度能更准确地反映社会保障制度和扶贫政策在缓解贫困问题和社会不公平中的作用,能更好地评估不同群体、不同地区之间的收入差别及其变化趋势。结论表明赛尔第二测度是一个比较理想的收入不平等测度和政策评价指标。
不平等测度;基尼系数;赛尔测度;赛尔第二测度
1.引言
正如阿玛蒂亚森所指出的,不平等测度既是一个简单的问题,又是一个复杂的问题[1]VII,简单是因为它不假思索的直观性,复杂是因为任何不平等测度都包含某种价值判断。不平等测度的研究最早是从Gini(1912)[2]8的工作开始,该文提出了基尼系数的概念,此后,基尼系数在收入分配不平等问题的研究中得到广泛使用,文献十分丰富。收入不平等的研究主要关注两类问题:其一是考察收入不平等的程度;其二是研究相关因素对不平等的影响程度,比如城乡收入差距、地区收入差异对全国收入差距的贡献大小。第一类问题主要涉及到基尼系数的测算问题,第二类问题与基尼系数的分解有关。在特定的数据条件下,基尼系数的分解也可以应用于基尼系数的测算问题。有关基尼系数的计算和分解问题已有广泛而深入的研究,关于后者的文献尤其丰富,国内外学者的相关工作可见Chakravarty (1990)[3]53,Cowell(2000)[4]39,Atkinsen(1970a)[5]244-263,Shorrocks(1984)[6]1369-1386,李实(1999,2002)[7]3-17,[8]84-87,陈宗胜(2002)[9]81-83,87,程永宏(2006,2007,2008)[10]109-120,[11]45-60,[12]124-144,金成武(2007)[13]149-158,胡祖光(2004)[14]60-69,万广华(2004)[15]64-69,董静、李子奈(2004)[16]120-123,李虎(2005)[17]127-135,洪兴建(2008)[18]307-324,张进峰、俞培果(2006)[19]142-143等。
从以往的研究知道,基尼系数没有令人满意的分解性质,即不能按人群进行分解。换句话说,基尼系数不能完全分解为组内差距与组间差距之和,因为有交叉项的存在。需要说明的是,这里对组间收入差距的定义是“所有人口都得到所在组的平均收入时的整体基尼系数”,这是最简洁且直观的定义。“抹掉”每组内部的收入差距之后,得到的基尼系数自然就代表组间差距。组间差距还有其他的定义和解释,但往往与“福利”联系起来,即不是“纯收入”意义上的比较。缺乏合理的分解性,这影响了基尼系数在第二类问题中的应用。*目前已有一些富有启发性的工作,比如程永红(2006,2008)。
基尼系数的另一个不足之处是,它没有合理的收入转移敏感性。实际上,两个个体之间的收入转移对基尼系数的影响程度取决于收入介于两者之间的人数,而不是取决于两者收入水平的高低,*见[20]121页。这样,较高收入之间的转移对基尼系数可能有更大的影响,这违反了“在分配低端应具有较强的敏感性”这一直观且合理的要求。针对中国居民收入问题的研究表明,基尼系数对较富裕阶层的收入变化比较敏感(万广华,2004),本文的分析表明,其中的原因在于基尼系数对于收入转移缺乏“弱敏感性”和“相对敏感性”,后者是本文引入的概念。在这个意义上,基尼系数并不是理所当然的不平等测度指标。
尽管如此,基尼系数仍然有很多好的性质,除了直观性(它在0,1之间,并且有直观的几何解释),基尼系数满足对称性、齐次性(均值无关性)、人口倍增不变性和庇古—多尔顿条件,这四个公理通常被认为是相对不平等测度应该满足的基本要求。在比较常用的不平等测度中,变异系数也满足以上四个公理,但没有合理的转移敏感性,因为它在各种收入水平上有同样的敏感性。对数标准差满足对称、齐次、人口倍增不变性,并且在较低收入水平上有更大的敏感性,但却不满足庇古—多尔顿条件。[20]27
很自然,我们希望能找到其他不平等测度,除了满足以上四个公理以外,还能满足更多的规范性要求,比如说,恰当的收入转移敏感性和分解性。分解性对于研究地区之间与群体之间的收入差距,以及这种差距对整体收入差距的贡献是十分有用的,分解性的作用就是把不同群体下的不平等测度“粘合”起来,进行跨群体的比较。
通常用到的分解性是塞尔可分解性,*根据权重的不同,有赛尔可分解性和广义赛尔可分解性。已有的研究表明,同时满足对称性、齐次性和赛尔可分解性的不平等测度只有广义熵(赛尔类)测度,*这里假设不平等测度是连续的,直观上说就是,每个个体收入的微小改变不会引起不平等测度的大幅度变动。如果是狭义赛尔可分解,则满足条件的测度必为赛尔测度的正倍数;如果是广义赛尔可分解,则有三种赛尔类测度满足条件,包括赛尔测度作为特殊情形。基尼系数被排除在外。由于变异系数和对数标准差没有恰当的敏感性或不满足庇古—多尔顿条件,对于不平等测度的选择与比较,可以侧重于基尼系数与赛尔类测度的比较,以及赛尔类测度之间的比较。对于不平等测度的比较问题,田士超(2007)[21]68-72做过初步的研究,但并未给出明确的结论。本文将从规范和实证两个角度对基尼系数和赛尔类测度类进行比较,并通过模拟实验和实证研究说明它们各自的优点和缺陷。
本文证明了,三个赛尔类测度中,只有赛尔第二测度(又称L指数)具有合理的收入转移敏感性。如果再加上分解性质的要求,仅有赛尔第二测度满足对称性、齐次性、人口倍增不变性、庇古—多尔顿条件,并且具有恰当的分解性和合理的收入转移敏感性。
在以往的研究中,三个赛尔类测度之间,人们往往更加偏好赛尔测度(T指数)而忽略了第二测度(L指数),但没有文献说明为什么在赛尔类测度中选择赛尔测度而不是赛尔第二测度的理由。实际上,如果我们接受Atkinsen(1970b)[22]70的观点“给定的收入转移在低端应该有更大的影响”,那么赛尔测度的收入转移敏感性是不合理的,也不符合人们的直观要求。但据我们所知,没有文献讨论赛尔第二测度的收入转移敏感性问题。本文的研究表明,赛尔第二测度有合理、直观的收入转移敏感性。
因此,首先在规范的意义上,赛尔第二测度是唯一的选择,至少是比基尼系数和赛尔测度更好的选择,这是本文的一个基本结论。其次,本文的实证研究表明,塞尔第二测度从应用的角度来看也是不平等测度的一个理想指标。最后,本文的模拟实验表明,赛尔第二测度对贫困人口的收入变动有较大的敏感性,表达了对贫困人口应有的关注,体现了“和谐社会”和“以人文本”的理念。这是由赛尔第二测度良好的规范性决定的。
本文其余部分安排如下:第二部分从规范性的角度对赛尔第二测度与基尼系数等其他测度进行比较,说明赛尔第二测度的优良性质;第三部分是对城乡收入差距的实证研究;第四部分根据实证结果对赛尔第二测度与基尼系数和赛尔测度作进一步的比较,验证赛尔第二测度在实践中的表现;第五部分通过模拟分析说明赛尔第二测度、赛尔测度和基尼系数对低收入群体收入变动的敏感性,进而展示赛尔第二测度对社会保障制度在缓解贫困问题和减轻社会不平现象所起作用的恰如其分的反映。
2.收入不平等测度的规范分析与不平等测度的选择
2.1不平等测度的规范性质与赛尔类测度

按照规范化的思路,需要确定不平等测度满足的基本要求。这涉及到社会福利的价值判断,但这不是本文关注的焦点。一般来说,不平等测度应该满足以下性质:
1.庇古—多尔顿条件。如果收入从穷人向富人转移,不平等测度应当增加。换句话说,如果向量y由向量x通过累积转移*我们称y是由x通过累积转移而得到的,如果对某个i和j, (1) xi≤xj,(2)yj-xj=xi-yi>0, (3) yk=xk对所有k≠i,j成立。获得,那么I(y)>I(x)。
2.对称性。如果收入向量y由收入向量x通过置换获得,那么I(y)=I(x)。也就是说,当任何两个个体交换收入时不平等测度仍然保持不变。
3.齐次性。如果向量y由向量x通过同比例增加获得,则I(y)=I(x)。 换句话说,对任意k>0,I(x)=I(kx)。
Fields和Fei(1978)[24]303-316把上面的三个性质作为相对不平等测度的“基本公理”。正如J.E.Foster(1983)所指出的,以上每个性质都是对I(x,n)孤立的限制,而没有涉及到跨群体的比较。跨群体比较的一个特殊情形是,一个地区通过复制的方法成倍扩张时(一个地区的复制是指人口数量和个体收入都不变)基尼系数的比较,人口倍增不变性也常常作为一个基本公理。*设x是收入分配向量,人口倍增不变性要求任意有限个x构成的收入分配向量有不变的不平等测度,即I(x,…,x)=I(x)。参见[1]139页。但人口倍增不变性考虑的是特定人口划分情况下不平等测度的跨区域比较问题,在一般情形下,为了把不同群体的不平等测度“粘合”起来,我们需要不平等测度具有某种分解性,最直观的是塞尔可分解性。狭义的赛尔可分解性可以描述如下:
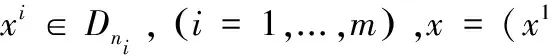
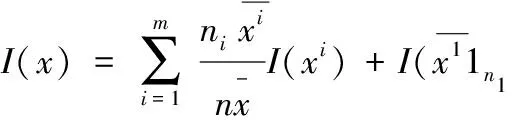
在这种情况下,我们称不平等测度I是收入“加权”可分(解)的。它的直观含义是整体的不平等可以分解为两个部分,即“组内”不平等的加权和与“组间”的不平等,这里的权重是收入份额。这里的“组间”不平等是指所有的个体均获得该组的平均收入时所对应的整体不平等测度,这在直观上是合理的,因为当每个组内部都消除了不平等时,整体不平等测度就是“组间”的不平等测度。
容易验证,狭义赛尔可分解性蕴含了人口倍增不变性。Bourguignon(1979)[25]901-920证明了,如果不计较一个常数倍数,塞尔测度是唯一的满足对称性、齐次性、二次可微性和狭义赛尔可分解性的不平等测度。*F Bourguignon的证明要求不平等测度二次可微,且非平凡。易知,赛尔测度满足庇古—多尔顿条件。Foster(1983)进一步去掉了在Bourguignon所加的二阶可微假设。*可微没有明确的经济含义,连续性假设似乎更合理。
但从价值观的角度,我们有理由对狭义赛尔可分解性提出批评,为什么组内不平等的加权和的权重是各组的收入份额?按照收入份额加权,意味着对富裕群体给予更多的关照。按照“公平”的原则,每个群体内部的不平等都应该平等对待,而不是“嫌贫爱富”,我们没有理由对较富裕群体内部的不平等给予更多的关注。
如果我们平等地对待每个组组内的不平等,那么组内不平等的加权和的权重应该由人口数量来决定。Shorrocks(1980)[26]613-626引入的广义可分性正是把人口作为权重决定的一个因素,具体说来,他考虑的广义可分的不平等测度是可以表示为“组内”不平等的加权和与“组间” 不平等之和的测度,其权重由每组人数与每组平均收入决定,不一定是“收入份额”。更精确地描述如下:


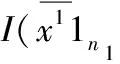
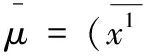
直观上看,一般赛尔分解式中的第二部分就是“组间”不平等测度,即假定每组的成员都获得该组的平均收入时的整体不平等测度,第一部分是各组不平等测度的加权和,它可以理解为各个组内的不平等对整体不平等的贡献。Shorrocks(1980)在不平等测度I满足可微性的前提下证明了*我们在另一论文中去掉了可微条件。,I(x;n)满足对称性、齐次性、人口倍增不变性和广义赛尔可分解性当且仅当它有如下形式*同时要求不平等测度对于完全平均分配取值为零,这是很自然的假设。:
其中A>0是常数。
以上测度统称为赛尔类测度,其中的第一个测度就是广义熵测度(Generalized entropy class of measure),第二个是塞尔测度(Theil measure),第三个称为塞尔“第二”测度(Theil’s second measure)[1]140。容易证明,当c→1时,广义熵测度变为赛尔测度,当c→0时,广义熵测度变为塞尔“第二”测度。
以上讨论表明,在规范的意义上,只需对赛尔类测度(共三类)进行比较,但从应用的角度,有必要将赛尔类测度与基尼系数进行比较。一方面,基尼系数应用的广泛性使其成为一个有用的参照,赛尔类测度与它的比较有助于我们对赛尔类测度的应用价值作出正确的评估;另一方面,如果仅仅因为不满足可分解性而排除基尼系数则缺乏足够的说服力。
2.2 赛尔类测度的敏感性分析
赛尔类测度之间的比较是基于它们对于收入转移的敏感性,具体地说,我们分别讨论广义熵测度、赛尔测度和赛尔第二测度的弱敏感性和相对敏感性。Atkinsen(1970b)认为,给定的收入转移在分配低端应有更大的影响,即不平等测度对低收入者之间的收入转移应该有更大的敏感性。弱敏感性的定义由Shorrocks等人(1987)[27]485-497给出,本文进一步引进了相对敏感性,并且我们将深入讨论赛尔类测度的弱敏感性和相对敏感性。*敏感性的精确表述是,积极的合成转移使不平等测度减少。积极的进步转移包含一个大小为a(a>0),从个人j到个人i的收入转移和一个大小为b(b>0),从个人k到个人l的收入转移,其中i、j、k、l的收入依次递增,并且转移前后总方差不变。不难证明,敏感性导致弱敏感性。但因为方差的定义有一定的随意性,故敏感性的直观性不强,而弱敏感性更合理更直观。相对于弱敏感性,敏感性的定义更复杂一些。
定义:称I满足弱转移敏感性,如果对任何满足xi
I(x)-I(x+(ui-uj)δ)>I(x)-I(x+(uk-ul)δ)>0
其中ui表示单位向量,第i个分量为1,其余的分量为0。*对不满足庇古—多尔顿条件的不平等测度讨论弱敏感性是没有意义的,所以要求积极的收入转移使不平等测度下降。
直观上说,收入绝对差距固定并且转移量相等时,低端收入者之间的收入转移使不平等测度的减小幅度更大。如果上述不等式反向成立,则称I具有逆向弱敏感性。比如说,收入2 000元的人向收入1 000元的人转移400元,或者收入10 000元的人向收入9 000元的人转移收入400元,其他人收入不变,弱敏感性意味着前者的不平等测度减少幅度更大。
我们现在引入相对敏感性,它与弱敏感性相互补充,能更全面地评判不平等测度的优良性,其定义如下:
定义:称I满足相对转移敏感性,如果对任何满足xi
I(x)-I(x+(ui-uj)δ)>I(x)-I(x+(uk-ul)δ)>0*对满足庇古—多尔顿条件的不平等测度讨论相对敏感性才有意义,所以要求高收入向低收入转移使不平等测度下降。
如果相反的不等式“<”恒成立,称I具有逆向相对敏感性。*相对敏感性与敏感性没有包含关系,相对敏感性与弱敏感性也没有包含关系。
相对敏感性有非常直观的意义。假设i和j的收入之比等于k和l的收入之比,i的收入低于k的收入,那么,相对敏感性要求i和j之间(充分小)的收入转移对不平等测度的影响程度大于k和l之间同等数量的收入转移对不平等测度的影响。即,收入相对差距相同并且转移量相等时,相对敏感性要求低端收入者之间的收入转移对不平等测度的影响更大。如果上述不等式反向成立,则称I具有逆向相对敏感性。这里,相对的含义是两对收入转移者之间的收入之比相等(弱敏感性考虑的情形是收入之差相等)。相对敏感性符合人们的直观判断。实际上,如果要求不平等测度是相对测度,即零次齐次的,同时满足广义赛尔可分解性,且组内不平等测度的系数由各组的人口数量来决定,这样的测度必定满足相对敏感性。*把i,j放在一组,称为第一组,k,l放在一组,称为第二组,其余人口放在一组(如果还有其余的人口),由于前两组不平等测度的系数相同,收入转移的影响取决于组内测度的变化。设收入转移量为δ,xk/xi=m>1,作为相对测度,可以把第二组收入都除以m,故收入转移对第二组来说仅相当于δ/m。所以第二组不平等测度的变化幅度更小。
比如说,考虑收入分配向量x0=(20,30,200,300),其中200/20=300/30=10,3号向1号转移收入10,收入分配向量变为x1=(30,30,190,300),4号向2号转移收入10,则收入分配向量变为x2=(20,40,200,290)。把1、2号放在一组,称为第一组,3、4号放在一组,称为第二组。如果要求不平等测度具有广义赛尔可分解性,则:
I(x1)=α·I(30,30)+β·I(190,300)+I(30,30;245,245)
I(x2)=α·I(20,40)+β·I(200,290)+I(30,30;245,245)
其中α、β由两组的人口数量和收入决定。若进一步要求α、β仅与各组人口数量有关,则α=β,作为相对测度(加上庇古—多尔顿条件),显然有:
I(200,290)>I(30,30)=0,I(20,40)=I(150,300)>I(190,300)
从而I(x2)>I(x1),这说明3号向1号的收入转移对不平等测度的减小幅度更大。也就是说,如果要求广义赛尔可分解性中每组不平等测度的系数完全由人口决定,则相对转移敏感性自动成立。因此,不平等测度具有相对敏感性是“以人为本”这一理念的必然要求。
本文的研究表明,赛尔类测度中,只有赛尔第二测度同时满足弱敏感性和相对敏感性。实际上,我们可得到如下结果。
命题:在广义熵测度、塞尔测度和塞尔第二测度中,只有塞尔第二测度同时满足弱敏感性和相对敏感性。更精确地说,赛尔类测度的弱敏感性和相对敏感性如下表所示:

表1 赛尔类测度的弱敏感性和相对敏感性
证明细节请参见附录2。
2.3不平等测度的比较与选择
2.3.1基于规范性的比较
在不平等问题的研究中,基尼系数是使用最广泛的不平等测度,国内研究尤其如此。虽然有时也用到其他测度,但都没有受到足够的关注,对不平等测度的选择缺少必要的论证。除了基尼系数,赛尔类测度也是近期研究中使用比较多的测度,但有关基尼系数与赛尔类测度的比较以及赛尔类测度之间的比较的研究很少,万广华(2004)的研究是很有启发性的,他从应用与测度分解的角度对较常用的不平等测度进行了比较,但在现有的文献中尚未发现基于规范性的比较,所以没有明确的结论。的确,要界定“最优不平等测度”是比较困难的,因为很难确定其客观标准。但我们认为基于规范性的比较是选择不平等测度的基础性工作。
从规范性的角度进行比较,我们的结论是很明确的,那就是,赛尔第二测度是比基尼系数更好的不平等测度,赛尔第二测度也是赛尔类测度(赛尔测度、赛尔第二测度和广义熵测度)中的最优测度。
前面的分析表明,赛尔类测度满足对称性、齐次性、人口倍增不变性。但赛尔类测度中满足庇古—多尔顿条件的只有赛尔测度、赛尔第二测度和c<1(c≠0)时的广义熵测度,也就是说c>1时的广义熵测度不满足庇古—多尔顿条件。*见 2.1或附录1。
由基尼系数的代数表达式知道基尼系数也满足对称性、齐次性、人口倍增不变性和庇古—多尔顿条件。*见加雷斯·D·迈尔斯著《公共经济学》,中国人民大学出版社,2001年1月,70—72页。所以,基于以上四个相对不平等测度的公理性质的比较,只能排除c>1时的广义熵测度。仅仅基于此难以看出赛尔第二测度与基尼系数之间的优劣,以及赛尔第二测度和赛尔测度之间的优劣。更进一步的比较是基于弱敏感性和相对敏感性。
本文第2部分(2.2)的研究表明赛尔类测度中同时满足收入转移弱敏感性和相对敏感性的只有赛尔第二测度I0。尽管赛尔测度满足弱敏感性,但不满足相对敏感性是赛尔测度的一个缺陷。事实上,赛尔测度具有逆向相对敏感性。直观上说,收入2 000元的人向收入1 000元的人转移400元的情形(其他人收入不变),与收入20 000元的人向收入10 000元的人转移收入400元的情形(其他人收入不变)比较,逆向相对敏感性意味着后者不平等测度减少幅度更大,这显然是不合理的。因此,从规范的角度来看,与赛尔测度比较,赛尔第二测度是更好的选择。
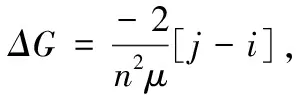
总之,从规范性的角度,赛尔第二测度是比赛尔测度和基尼系数更好的不平等测度。
2.3.2 基于实践性的比较
在实践中,基尼系数的使用非常广泛,国内有关收入差距的研究中基尼系数的使用是最多的,国外文献也有一些使用其他不平等指标的研究,但使用基尼系数的也更普遍一些。原因之一是它的直观性,另一个原因或许是因为锁定效应。同时,对于基尼系数的计算方法,已有十分广泛而深入的研究,相关文献可见胡祖光(2004)、程永宏(2006,2007)和李虎(2005)等。这些研究成果也进一步促进了基尼系数的应用。
与此形成对照的是,对赛尔第二测度构造的经济动因和计算缺乏深入的研究,这是它没有得到普遍运用的原因之一。如果能解决赛尔第二测度的计算问题,其良好的性质会使它得到更好的应用。幸运的是,以当今计算机的计算能力来说,基尼系数和赛尔类测度的计算并无难易之分,关键的问题是数据的可得性。比如说,利用国家统计局公布的城乡居民收入的分组数据,通过拟合分布函数的方法,很容易计算出基尼系数和赛尔类测度,包括赛尔第二测度。因此,从应用的角度,赛尔第二测度也是可行的选择,并不逊于基尼系数。
赛尔测度与赛尔第二测度比较,两者计算的难易程度没有区别,但文献中如果用到赛尔类测度,选择的往往是赛尔测度而不是赛尔第二测度,比如,田士超(2007)等文献使用了赛尔测度研究与地区收入差距有关的问题。如果在赛尔测度(熵指数)和基尼系数之间选择赛尔测度,其理由往往是赛尔测度良好的分解性质,但在赛尔测度和赛尔第二测度之间选择前者却缺少理由,很少有文献说明为什么选择赛尔测度而不是同样具有良好分解性质的赛尔第二测度。其中的一个原因或许是因为赛尔测度与信息经济学中“熵”的联系,但我们认为最根本的原因是由于对赛尔第二测度缺乏深入研究,实际上,据我们所知,有关赛尔测度和赛尔第二测度比较的研究很少,我们尚未见到从规范性的角度进行比较的研究。前面的分析已经表明,赛尔第二测度的规范性质更令人满意,因为它有一个赛尔测度没有的性质,这就是相对敏感性。
结论是,从计算和应用的角度,塞尔第二测度并不逊于赛尔测度,而且前者有更合理的收入转移敏感性。后面的模拟实验将进一步显示,赛尔第二测度的收入转移敏感性使其在实践中有良好的表现。*参见第5部分的讨论。
2.3.3基于价值观的分析
事实上,在2.3.1中,基于规范性的比较也有价值观的内涵,但从基尼系数和赛尔类测度的表达式,我们可以更好地理解其背后的价值观。
我们首先考察赛尔第二测度、赛尔测度和一般广义熵测度的分解公式。仍然假定给定群体的人口数量为自然数n≥2,划分为m个非空子组,人口数量分别为n1,…,nm,收入分配向量分别为x1,…,xm,则(可直接验证):
由以上分解公式知道,赛尔类测度都可以表示为组间不平等测度与各个组内不平等测度的加权和,其权重体现了某种价值判断。
赛尔第二测度中,权重是人口份额,赛尔测度中,权重是收入份额。背后的含义是,在进行群体比较时,赛尔测度关注群体的收入比重,赛尔第二测度关注人口份额,即强调人与人之间的平等,而广义熵测度是两者的“折衷”,当c从1变为0时,权重由收入份额变为人口份额,群体收入份额的作用越来越小,最后变为人口份额。也就是说,赛尔第二测度平等地对待高收入群体内部和低收入群体内部的不平等,体现了以人为本的精神。所以,在“人人平等”的价值观下,赛尔第二测度是赛尔类测度中最合适的选择。*只有当c=0或1时,组内不平等测度的权重之和才等于1,在其他情形,权重之和不等于1,这也说明广义赛尔类测度的分解并不令人满意。

综上所述,从表达式看,与基尼系数和赛尔测度相比较,赛尔第二测度更好地体现了“社会和谐”与“以人为本”的理念。
2.3.4 赛尔第二测度的直观性
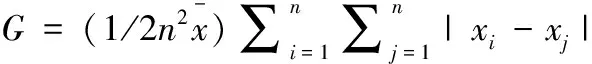
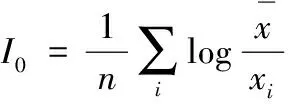
它可以看作是每个个体与平均收入的“差距”之和,也可看作每个个体的“相对不平等”负效用之和,是全社会的负效用。当某个体的收入大于平均收入时,相对不平等负效用为负;*高于平均收入的个体从不平等中得到的效用是一个负效用的反数。当收入小于平均收入时,相对不平等负效用为正;当收入等于平均收入时,相对不平等效用为零。另一方面,赛尔第二测度可以写成:
即赛尔第二测度是收入的算术平均数与几何平均数之比的对数。我们知道,若干个正数的几何平均值小于或等于算术平均值,当总量一定时,分配越平均,几何平均值越大,完全平均分配使得几何平均值最大(与算术平均值相等)。所以,算术平均值与几何平均值之比能刻画不平等的程度。

上面的分析表明,赛尔第二测度不仅有良好的规范性质,而且从价值观、实践性和直观性的角度,也是理想的不平等测度。在第三部分,我们将通过城乡收入差距的实证研究进一步考察赛尔第二测度的表现。
3.城乡收入不平等的实证分析
3.1赛尔第二测度、赛尔测度和基尼系数的连续型计算式
根据第二部分的分析,我们选取塞尔第二测度来实证研究我国2000年以后的城乡收入不平等的情况,并利用其他测度作为分析的参照。本文使用的数据均来自各年《中国统计年鉴》和中国统计局网站公布的居民收入分组数据,其中农村居民的收入数据为20组,城镇居民的收入数据为8组。*2008年(含2008年)之前,农村居民5 000元以上的分布缺少详细信息,从2009年开始,农村居民收入数据包含了20 000元以下的分布信息。
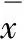
分析我国城乡收入差距时,m=2,全国居民收入差距可以分解为城镇居民内部收入差距、农村居民内部收入差距和城乡收入差距三部分。
使用分组数据计算I0时,由于没有微观数据,如果按照离散公式计算,只能视每组成员有相同的收入,这样会忽略组内的不平等。为了克服这个不足,我们使用连续形式的计算公式。由I0的离散表达式:
设F(x)是累计收入分布函数,则得到I0的连续表达式:
同理可以得到基尼系数、赛尔测度的连续型计算公式:


只要比较精确地拟合了收入分布函数F(x),由以上计算公式得到的几种不平等测度就具有较高的精确度。
3.2计算方法说明与计算结果
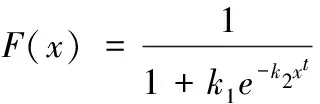
据此计算的基尼系数G、塞尔测度I1及赛尔第二测度I0的一些结果包含在表2—4中,关于广义熵测度Ic(c=0.5)的计算结果没有在表中列出。在计算中,利用了以下等式:
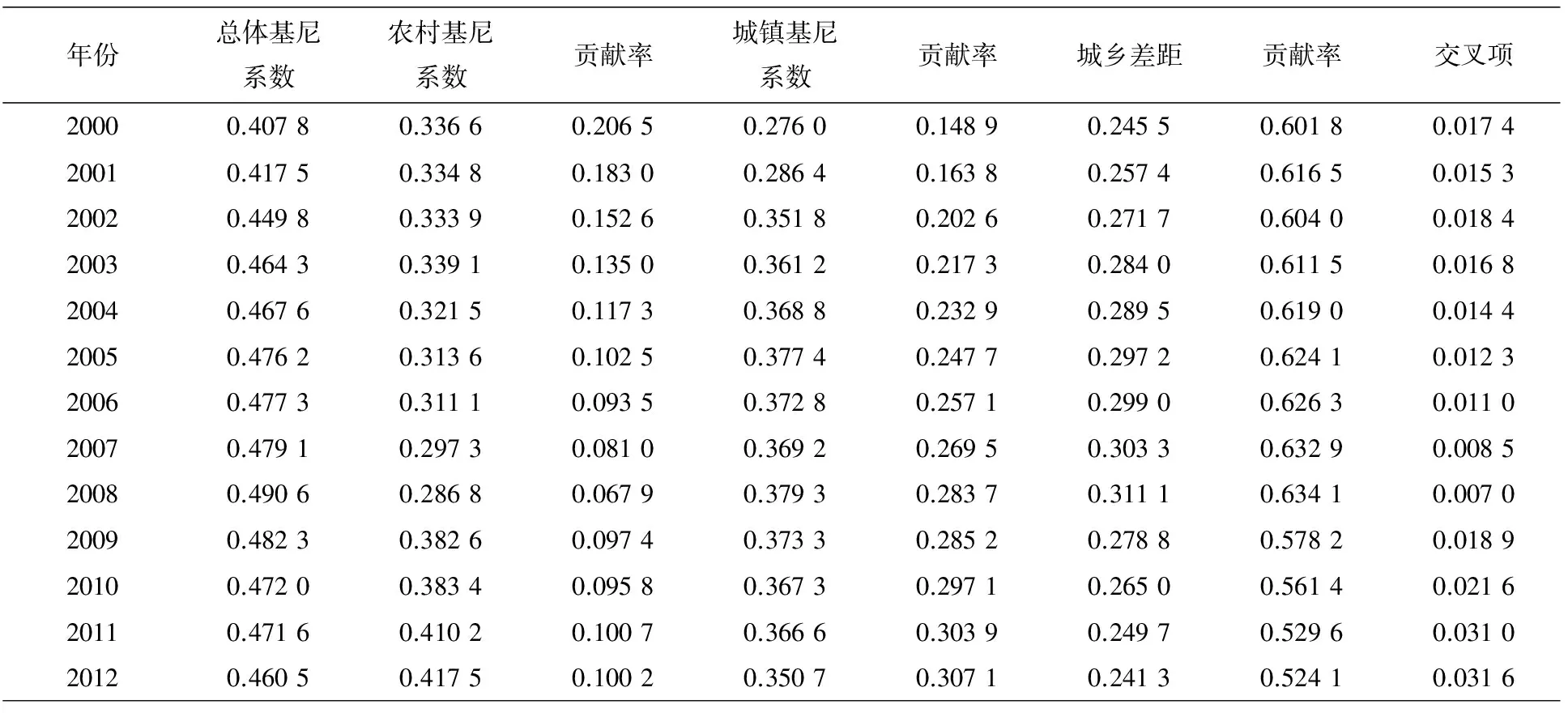
表2 基尼系数G的计算结果
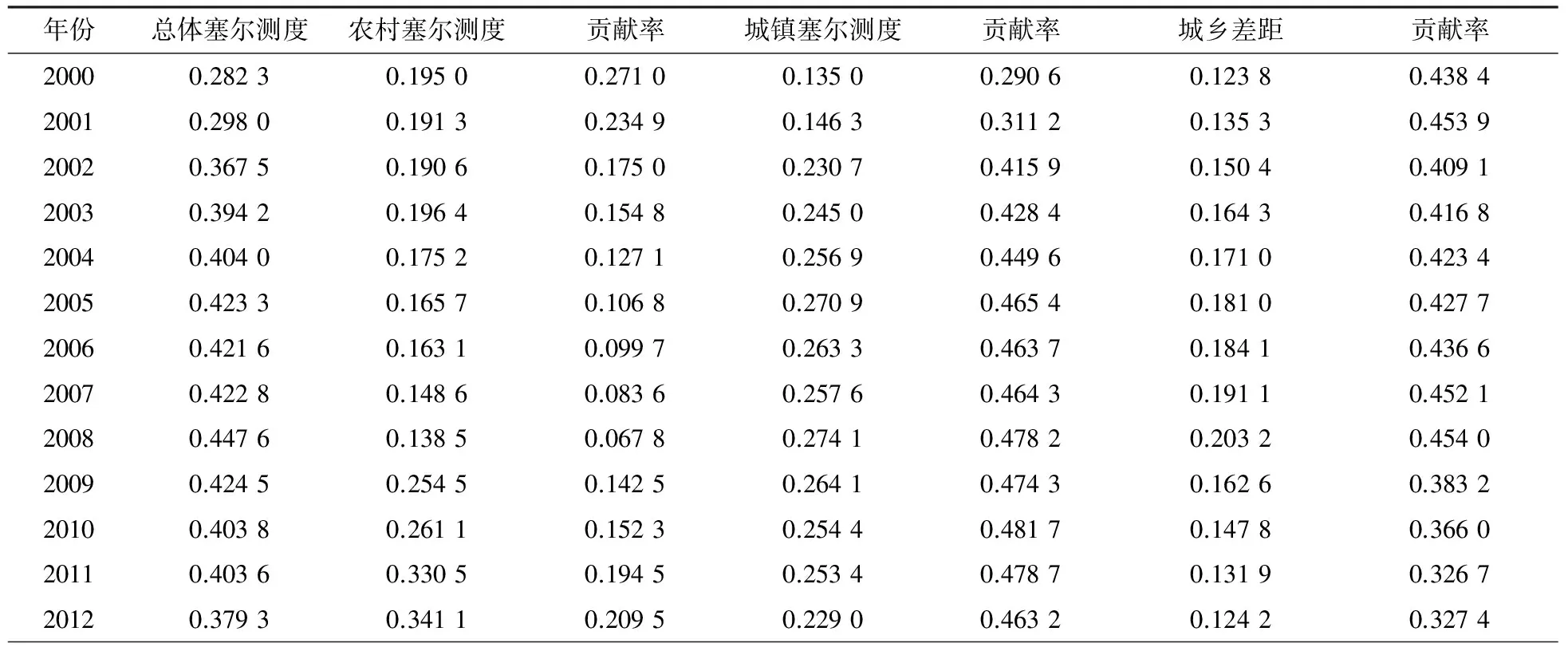
表3 塞尔测度I1的计算结果
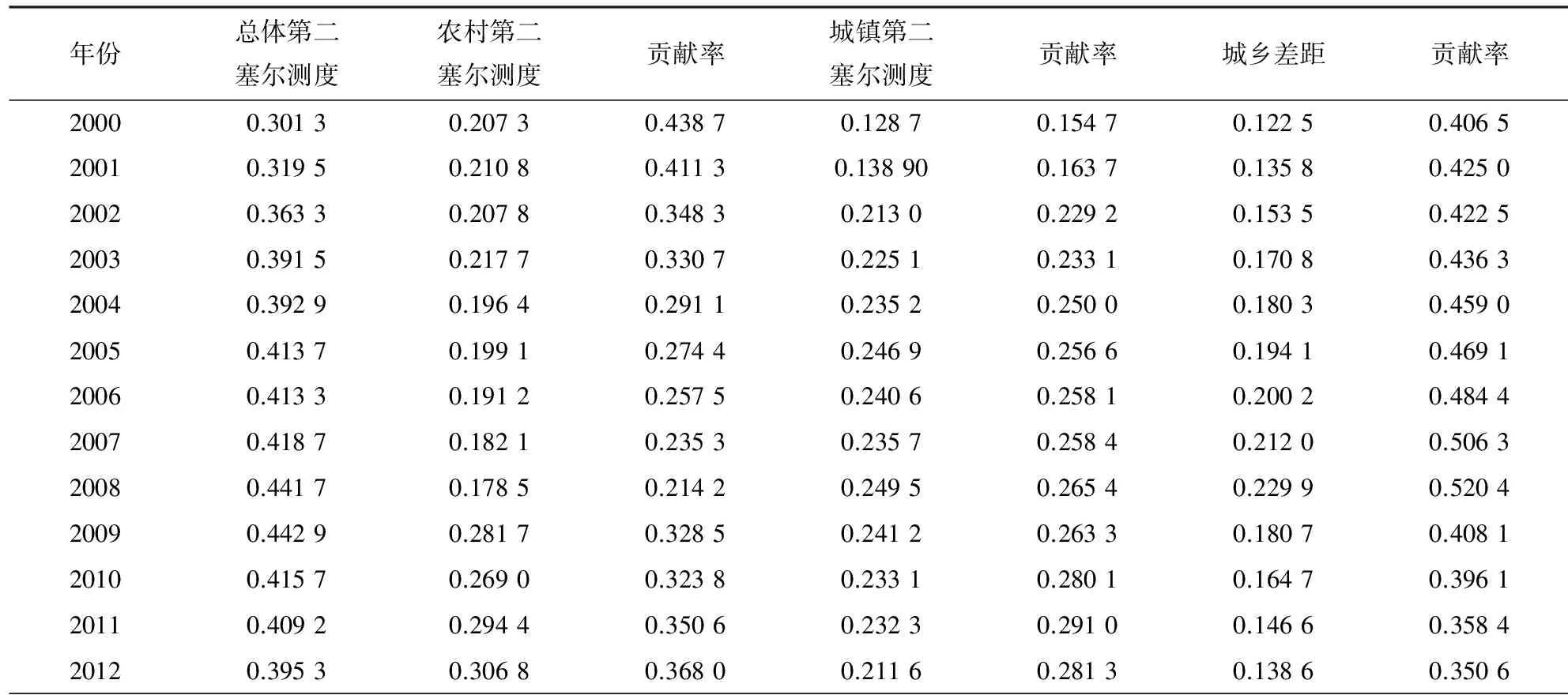
表4 塞尔第二测度I0的计算结果
4. 计算结果的解释与几个不平等测度的进一步比较
4.1 计算结果的解释
从2000年到2009年,全国的基尼系数、赛尔测度、赛尔第二测度和广义熵测度Ic(c=0.5)都是逐步增加的,2009年达到最高点(赛尔测度最高点是2008年)。从2009年到2012年,全国基尼系数和赛尔第二测度呈现下降趋势。另一方面,从2000年至2008年,所有的测度都显示农村内部收入差距是下降的,城镇内部收入差距和城乡收入差距是逐步上升的,从2008年到2012年变化趋势反转,即农村内部收入差距逐步上升,城镇内部收入差距和城乡收入差距逐步下降。这些变化特征表明政府的农村扶贫、减税政策取得了较好的成效;近几年城镇收入差距和城乡收入差距的缓慢下降表明行业收入差距、不同阶层收入差距扩大的趋势已被基本控制。
仅从变化趋势上来看,很难区分这几个不平等测度的表现。
首先,需要对城乡收入差距的定义作进一步的说明。从逻辑上看,收入差距是由农村内部收入差距、城镇内部收入差距和城乡收入差距构成的。消除农村和城镇的内部差距之后所计算的不平等测度就代表了城乡差距,换句话说,所有农村居民和城镇居民分别得到农村和城镇的平均收入后的整体不平等测度就是城乡差距。*群体之间的收入差距有其他的定义方式,但这不是本文关注的重点。
4.2 赛尔第二测度与基尼系数计算结果的比较
先看基尼系数的计算结果。代表城乡收入差距的基尼系数从2000年的0.245 5上升到2008年的0.311 1,在这期间的每一年,代表城乡差距的基尼系数都小于或接近农村和城镇的基尼系数,*2000年至2008年,城乡差距的基尼系数都小于城镇的基尼系数,2000年至2006,城乡差距的基尼系数也小于农村基尼系数,在2007和2008年,城乡差距的基尼系数略大于农村基尼系数。但城乡收入差距对全国收入差距的贡献却占到60%以上,且贡献率比较稳定。换句话说,尽管农村和城镇的基尼系数都比城乡收入差距基尼系数大,但对全国收入差距的贡献之和却小于40%。这与直观上的判断不吻合。其中的原因是农村内部和城镇内部收入差距的权重太小。由于交叉项很小,全国基尼系数主要是由城乡差距与一个加权和组成,也就是农村基尼系数和城镇基尼系数的加权和,其权重是收入比例与人口比例之积,如果将这一加权和解释为城乡内部收入差距,由于权重之和小于0.5,*由城乡人口比例和收入比例测算,数据来源于国泰安数据库。如果权重之和为1,则将其视为城乡内部差距是比较合理的。那么就意味着农村和城镇的基尼系数被赋予的权重太小。这是基尼系数固有的缺陷。
再看看农村和城镇收入差距对全国收入的贡献。农村收入差距的贡献率从2000年的20.7%递减至2008年的6.8%,城镇收入差距的贡献率从2000年的14.9%增加到2008年的28.4%,这两个贡献率都低于直观上的判断(因为城乡内部的收入差距均大于或接近城乡收入差距),这也是农村、城镇基尼系数权重太小所导致的结果。城乡收入差距对全国收入差距的影响确实比较大,但贡献率超过60%有夸大之嫌。实际上,以2007年为例,如果同比提高农村人口的收入使得城乡收入差距为0(使农村平均收入等于城镇平均收入),则此时的全国基尼系数描述的收入差距由农村内部和城镇内部的收入差距构成,而模拟计算表明此时全国基尼系数约为0.331 8,*提高比例为城镇居民平均收入与农村居民平均收入之比,约为3.776。同比提高农村居民收入后基尼系数的计算按第5部分的方法进行。但2007年的基尼系数为0.479 1,减去63.29%(城乡差距的贡献率)后为0.175 9,与0.331 8是不吻合的。就是说,如果消除城乡收入差距,但保持城镇和农村内部收入差距不变(农村居民收入同比例提高,城镇居民收入不变),则基尼系数应为0.175 9,而模拟计算的结果却是0.331 8。表面上,这是基尼系数不合理的分解性造成的,但根源却在于基尼系数对低收入群体赋予的权重太小,基尼系数的这一缺陷不会因为它存在其他分解方式而消失,是本质性的。
再看赛尔第二测度的计算结果。计算显示,2007年城乡收入差距的贡献率为50.63%,如果按上面的方法消除城乡差距,则赛尔第二测度应为0.418 7×(1-50.63%)=0.206 7,它与城乡内部的收入差距是吻合的,这是由赛尔第二测度的分解性质决定的。从2000年到2008年,城乡收入差距的贡献率从40.65%上升至52.04%,其增速比基尼系数所显示的大,这更符合我们的直观判断。实际上,在这一阶段,全国赛尔第二测度有近41%的上升幅度。注意到,在这一阶段农村收入差距略有下降,而城镇收入差距和城乡收入差距有相近的上升幅度,城乡收入差距的贡献率从40.65%上升至52.04%是比较合理的判断。但按基尼系数的计算结果,城乡收入差距的贡献率从60.18%上升至63.41%,贡献率的变化幅度与塞尔第二测度相比,明显偏小。
4.3 赛尔第二测度与赛尔测度的计算结果的比较
2000—2001年、2010—2011年,农村赛尔测度均超过了城镇赛尔测度,但以赛尔测度计算的农村收入差距的贡献率却低于城镇收入差距的贡献率,其中2010—2011年农村塞尔测度的贡献率远远低于城镇赛尔测度的贡献率。在这些年份中,农村人口的数量大于城镇人口的数量,赛尔测度显示的结果是明显不合理的。赛尔第二测度显示的结果正好相反,即农村收入差距的贡献率大于城镇收入差距的贡献率,且2000、2001年超过的幅度很大,这符合我们的直观认识,因为2000—2001年农村赛尔第二测度超过城镇赛尔第二测度的幅度达50%(赛尔测度也是如此)。就是说,赛尔第二测度的贡献率准确地反映了这些年农村不平等程度更严重的事实。
究其原因,是因为赛尔测度与基尼系数一样,对农村不平等没有给予应有的重视。赛尔测度的分解公式中,组内赛尔测度的权重是收入份额。正是因为把收入份额变成人口份额,塞尔第二测度在度量不平等程度时对贫困人口给予了应有的重视,体现了“以人为本”的理念。如果以赛尔第二测度作为政策参照,那么,降低收入差距的有效手段之一就是提高贫困人口的收入,这也符合一般的直观判断,符合“和谐社会”的价值观。
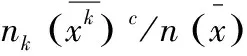
5.模拟分析
为了进一步比较基尼系数、赛尔测度和赛尔第二测度在实践中的表现和特性,我们通过对现实收入分配结构的模拟来检验三种测度对收入结构变动的敏感性,对社会救助和社会保障强度的敏感性,进而比较三种测度在测算中国居民收入不平等程度时的表现。
5.1 试验设计

根据该收入分配方案计算的全国基尼系数、赛尔测度和赛尔第二测度分别为g=0.478 9,s=0.420 8,s2=0.425 1,这与按分布函数计算的结果(0.479 1,0.422 8,0.418 7)非常接近。我们要测算的是收入结构变化所引起的三种不平等测度的变动幅度,由此可以分析三种不平等测度对收入结构变动的敏感性。
先说明一些基本数据。把农村和城镇人口混合起来,按收入从低到高的顺序排列,i=1是最低收入者,i=132 129是最高收入者,用y(i)表示i的收入,模拟计算表明y(5 000)=1 286.2,y(10 000)=1 837.7,y(15 000)=2 244.6,y(20 000)=2 589.3,平均收入为m=9 169.5。
5.2 试验结果分析与结论
1998年,城镇最低收入保障制度在全国推广,2007年开始建立农村的低保制度。低保制度为保障贫困居民基本生活需求,维护社会稳定发挥了重要作用,产生了良好的社会效益。因此测算基尼系数、赛尔测度和赛尔第二测度对低保制度的敏感性是很有意义的,也是对它们进行比较的重要依据。2009年3季度全国农村低保标准为年人均 1 179.2元(月人均98.1元),*数据来源:《2009年3季度全国民政事业统计数据》,民政部网站。最低的只有 600多元,最高的 2 000多元(公维才,2009)。[28]113-115低保政策对满足贫困人口最起码的生存需求是非常重要的,也是促进社会和谐的重要举措。我们考察以上三种不平等测度对它的反应。 把y(4 266)=1 179元作为最低收入标准,*根据收入分布函数推算,低于该标准的城镇人口仅有124万,而低于该标准的农村人口有4 142万。即把所有收入低于这个标准的人口的收入都提高到1 179,其他人的收入不变,则基尼系数、赛尔测度和赛尔第二测度分别由之前的0.478 9、0.420 8、0.425 1变为0.476 5、0.416 1、0.394 2,变化率分别为0.5%、1.12%、7.27%(与没有实施低保政策的原始分配方案相比较,下同)。
我们看到,赛尔第二测度对低保政策作出了比较明显的反应,但基尼系数和赛尔测度的反应比较迟钝。尽管1 179是一个较低的标准,但对于低收入人群来说,它解决了最贫困的占全国3.2%的人口的基本生存问题(平均补贴462元),其作用是不可或缺的。赛尔第二测度的反应是恰当的,而赛尔测度和基尼系数反应太弱。
2008年年底,我国宣布将扶贫标准从人均年收入786元提高至1 067元,2009年提高到1 196元。但按世界银行推荐的贫困标准(人均每天1.25美元),目前的低保标准仍然是偏低的,有待进一步提高。如果把最低收入提高到y(20 000)=2 589.2,则基尼系数、赛尔测度和赛尔第二测度分别为0.459 0、0.391 4、0.347 0,变化率分别为4.16%、7%、18.4%。*2 577.76仍是偏低的标准,因为它仅占平均收入(9 062.95)的28.2%。 但从中国的实际情况来看,要实现这个目标,尚需时日。倘若把最低收入标准提高到平均收入的一半(4 584.7元),不足者补齐差额,则低保制度覆盖5.22亿人口,相应的基尼系数、赛尔测度和赛尔第二测度分别下降为0.394 0、0.316 4和0.253 8,下降的幅度分别为19.8%、24.8%、40.3%。平均收入的一半是国际上通行的贫困标准,如果我国能把低保水平提高到这个标准,就较好地解决了贫困问题,*2007年农村居民的平均收入为4 140元。数据来源:《农民日报》,2008-01-25。这样的话,城乡人均收入之比将由低保前的3.77:1变为2.94:1,*城乡差距之基尼系数由0.303 2变为0.254 5,赛尔测度由0.191变为0.132 6,赛尔第二测度由0.211 8变为0.141 4。农村高低收入比由低保前的2.08变为1.18,这说明农村内部居民收入差距大幅度缩小,*计算两两收入比(高收入与低收入之比),再计算几何平均值。直观上,农村高低收入比就是在平均意义上较高收入与较低收入之比,这一测度在低保前后的变化说明低保政策使农村收入不平等的现状有了根本的改善,这对于缩小全国收入差距应该有很大的影响,因为农村人口占比为54%。并且城镇居民收入差距也略有下降。*城镇基尼系数从0.368 8变为低保后的0.361,赛尔测度从0.255 1变为0.245,赛尔第二测度从0.235 1变为0.213 9。在收入不平等的状况得到极大改善的情况下,唯有赛尔第二测度所显示的40.3%的下降幅度是比较恰当的反映。
由以上实验结果容易看出,赛尔第二测度对社会低保政策最敏感,或者说,赛尔第二测度恰当地反映了扶贫政策对缓解贫困问题和不平等现象的基本而重要的作用。因此,如果要选择不平等测度作为扶贫政策的依据,或者评估扶贫政策的效果,赛尔第二测度是一个恰当的测度。
基本结论与评述:以上的模拟实验表明赛尔第二测度在实践中表现出对贫困人口收入变动恰当的敏感性,对社会保障制度和扶贫政策在缓解不平等问题中的作用有恰如其分的反映。这是其弱敏感性和相对敏感性在实践中的体现。赛尔第二测度的以上特性以及它良好的规范性是我们判断“塞尔第二测度是比基尼系数、赛尔测度等其他测度更优良的不平等测度”的依据。重要的是,赛尔第二测度对贫困人口的关注所体现的是“人人平等”的理念,这正是“和谐社会”的一个基本要义。
有关基尼系数分解方式的研究很多,这些研究对于理解群体或地区之间的收入差距是很有帮助的,也有助于研究不平等的各种影响因素。但基尼系数“轻视”贫困人口的根本缺陷不可能通过某种分解而克服,因为它是基尼系数本身所固有的。所幸的是,赛尔第二测度是一个好的替代。随着研究和认识的深入,我们相信赛尔第二测度会得到更广泛的应用,在不平等问题的研究中发挥更重要作用。
[1] Amartya Sen. On economic inequality[M]. Oxford New York: Clarendon Press, 1973.
[2] Corrado Gini. Variabilita e Mutabilita[M]. Bologna: Tipografia di Paolo Cuppini, 1912.
[3] S R Chakravarty. Ethical Social Index Numbers[M]. New York: Springer Verlag, 1990.
[4]F A Cowell. Measuring Inequality[M].Oxford:Oxford University Press,2011.
[5]A B Atkinsen.On the measurement of inequality[J].Journal of Economic Theory,1970a(2).
[6] A F Shorrocks. Inequality Decomposition by Population Subgroups[J].Econometrica,1984(52).
[7]李实,赵人伟. 中国居民收入分配再研究[J]. 经济研究, 1999(4).
[8]李实. 对基尼系数估算与分解的进一步说明——对陈宗胜教授评论的再答复[J]. 经济研究,2002(5).
[9]陈宗胜. 关于总体基尼系数计算方法的一个建议——对李实研究员《答复》的再评论[J]. 经济研究,2002(5).
[10]程永宏.二元经济中城乡混合基尼系数的计算与分解[J].经济研究,2006(1).
[11]程永宏. 改革以来全国总体基尼系数的演变及其城乡分解[J]. 中国社会科学,2007(4).
[12]程永宏. 基尼系数组群分解新方法研究:从城乡二亚组到多亚组[J].经济研究,2008(8).
[13]金成武. 离散分布收入数据基尼系数的矩阵向量形式及相关问题[J]. 经济研究,2007(4).
[14]胡祖光. 基尼系数理论最佳值及其简易计算公式研究[J]. 经济研究,2004(9).
[15]万广华. 收入分配的度量与分解:一个对于研究方法的评介[J]. 世界经济文汇,2004(1).
[16]董静,李子奈. 修正城乡加权法及其应用——由农村和城镇基尼系数推算全国基尼系数[J].数量经济技术经济研究,2004(5).
[17]李虎. 关于基尼系数分解分析的讨论[J]. 数量经济与技术经济,2005(3).
[18]洪兴建. 一个新的基尼系数子群分解公式——兼论中国总体基尼系数的城乡分解[J]. 经济学季刊,2008(10).
[19]张进峰,俞培果. 按人群分组计算全国基尼系数:一种矩阵分解方法[J]. 统计与决策,2006(12).
[20]Amartya Sen. 论经济不平等,不平等之再考察[M]. 北京:社会科学文献出版社,2006.
[21]田士超. 上海市的收入差距:基于泰尔指数分解的分析[J]. 世界经济情况,2007(10).
[22]A B Atkinsen .Poverty in Britain and the Reform of Social Security[M].Cambridge:Cambridge University Press,1970b.
[23] Foster J E. An axiomatic characteristic of the Theil measure of income inequality[J]. Journal of Economic Theory, 1983(17).
[24]Fields G S, Fei J H. On equality comparisons[J]. Econometrica,1978(46).
[25]Bourguignon F. Decomposable Income Inequality[J]. Econometrica,1979(47).
[26]Shorrocks A F. The Class of Additively Decomposable Inequality Measure[J]. Econometrica,1980(48).
[27]Shorrocks A F,Foster J E. Transitive sensitive inequality measures[J]. Reviews of Economic Studies,1987(54).
[28]公维才. 健全我国农村最低生活保障制度的基本思路[J]. 改革与战略,2009(1).
责任编辑:廖文婷
以赛尔测度为例,其他相同。
不妨假设A=1。假设收入从较高的xj向xi转移且不改变相对贫富地位,即转移量δ满足xi+δ 附录2:2.2中命题的证明 证明:不妨假设A=1。前面已经指出(见2.1或附录1),当且仅当c1的赛尔类测度才满足庇古—多尔顿条件,因此敏感性和相对敏感性的讨论只需针对c1的赛尔类测度。 假设收入从较高的xj向xi转移且不改变相对贫富地位,即转移量δ满足xi+δ 先讨论弱敏感性。令xj-xi=t>0(常数)。 当c=1时, 当c=0时, 当c≠0,1时, 当c=1时, 这表明等量的收入转移在低端对I0的影响更大,从而赛尔第二测度I0具有相对敏感性。 当c≠0,1时, 总之,对于Ic而言,c≥1时逆向敏感性成立;0 以上讨论可以得到表1的结果,由此可知,同时满足弱敏感性和相对敏感性的赛尔类测度只有赛尔第二测度。命题得到证明。 The Study on Choice of Inequality Measures of Income and the Empirical Verification Based on the Data from China GONG Zhi-min,XIONG Wei-yi (Business School,Xiangtan University,Xiangtan,Hunan 411105,China) From normal and positive perspect, it is shown that Theil’s second measure is a better measure than Gini coefficient and Theil measure. The theoretical analysis and simulation experiment show that Theil’s second measure has appropriate sensitivity to the changes of income of the people with low income. Compared with Gini coefficient and other inequality, Theil’s second measure can reflect more precisely the effect of social security system and social assistance system in alleviating unfairness in the society, and by using it the income gap between different groups and between different areas can be estimated more precisely. The conclusion of this paper is that Theil’s second measure is a good inequality measure and policy evaluation index. inequality measure;Gini coefficient; Theil measure; Theil’s second measure 2016-01-14 龚志民(1962-),男,湖南常德人,理学博士,湘潭大学商学院教授、博士生导师。 熊唯伊(1984-),女,湖南株洲人,湘潭大学商学院博士研究生。 国家社科基金重点项目“我国收入分配体制改革动态跟踪和效果评估研究”(项目编号:08AJL008);湖南省社科重点项目“我国收入分配体制改革的理论基础和效果评估体系研究”(项目编号:13ZDB13)。 F224 A 1001-5981(2016)04-0064-13