DNA自组装计算模型求解二部图完美匹配问题

蓝雯飞 邢志宝 黄 俊 强小利

(中南民族大学计算机科学学院 武汉 430074) (lanwenfei1@163.com)



DNA自组装计算模型求解二部图完美匹配问题

蓝雯飞 邢志宝 黄 俊 强小利

(中南民族大学计算机科学学院 武汉 430074) (lanwenfei1@163.com)

针对二部图完美匹配问题，提出了一种基于DNA计算自组装模型的算法.首先，通过该算法求解了一个具有10个顶点的二部图完美匹配问题的实例,实例中给出DNA计算自组装模型算法所涉及到的DNA Tile的编码设计方案、自组装计算步骤及结果分析;然后，给出了任意二部图完美匹配问题的求解方案;最后，针对DNA计算自组装模型算法解决任意二部图完美匹配问题的时间和空间消耗进行了讨论.结果表明:对任意二部图只需14种Tile类型就能够得到完美匹配.

完美匹配；二部图；DNA计算；自组装；瓦片

在计算面临的三大类问题(即容易、困难和不可计算)中，对于容易问题，传统电子计算机可以轻松地处理，但是对于困难问题(一般指NP-完全问题)，计算时间将会随着计算规模的增大而呈指数增长.针对这个问题，很多科学家将目光转向对其他类型的计算机结构研究上，从而类似于神经网络计算机[1-2]、量子计算机[3-4]以及DNA计算机模型[5-11]等应运而生.DNA计算机模型，凭借其高度的并行计算能力和海量的存储能力在各种新型计算机中脱颖而出,在很多领域(比如生物、物理、数学及计算机科学)中都得到了广泛的应用，并成为解决NP难问题的一种潜在的方案.

早在20世纪60年代，Feynman[12]就已经提出了在分子水平上进行计算的概念，但是这种观念真正引起各个领域科学家的兴趣是在Adleman[13]提出利用DNA计算解决有向Hamilton路径问题之后.Aldeman不但解决了Hamilton路径问题，还成功地利用现代生物技术进行了实验.自此，DNA计算引起各领域科学家的极大兴趣以及社会各界的广泛的关注和支持.1998年，Winfree[14]提出了一种既具有Seeman的分支DNA结构又具有Wang Tiling理论的可以自组装的DNA结构.2009年张勋才[15]通过编码Tile粘性末端，将待运算的信息与Tile的结合域相结合，建立了基于DNA计算的减法和除法运算模型,其中除法模型中包含了比较、复制和减法3个子系统.作者利用DAN计算模型实现了这3个子系统并将其合并最终成为了一个完整的除法模型.此外，还利用自组装DNA计算模型解决了0-1规划问题和图着色问题.在解决0-1规划问题时，作者将0-1规划问题中的约束机制分成了“与”操作和“比较”操作2个基本操作，并利用DNA自组装模型实现了这2种操作.通过这2种操作的组合，可以自动判断任意可行解是否满足给定的约束条件.在图着色上，作者引入了非确定性算法，利用DNA自组装的高度并行的特性，验证所有可能的着色方案，在多项式时间内就可以解决图着色问题.2009年，陈智华[16]利用DNA自组装模型提出了一次一密密码系统.该系统由4个子系统组成：加密子系统、密码提取子系统、秘钥计算子系统和解密子系统，同时利用生物技术实现了秘钥的安全传输.另外，通过对DNA Tile的编码实现了破译Diffie-Hellman算法的DNA自组装模型.通过生物技术(PCR和凝胶电泳)读出素数原根的离散对数值，从而威胁Diffie-Hellman密钥交换安全.但是由于Tile的种类与输入位数呈线性关系，限制了该方案对大规模输入的应用.2008年，Brun[17]基于DNA自组装计算模型提出了2个系统，解决了NP-完全问题——k-SAT，并以3-SAT为例进行了说明.作者提出的第1个Tile系统用了Θ(n2)种不同的Tile表示布尔方程式中n个不同的变量;第2个Tile系统仅用64=Θ(1)种不同的Tile表示具有n个变量的布尔方程式，大大降低了自组装运算的空间消耗.运算时，根据Tile的编码及运算规则随机形成解空间，再通过解空间中的每个解对布尔方程中的每个变量进行扫描，确定解空间的正确性.同年，他又用49种不同的Tile，建立了用于求解子集和问题的DNA自组装计算模型[18].

二部图匹配问题是图论中的热点问题，在解决各个领域的问题中也得到了广泛的应用.在二部图匹配问题中,除了匈牙利算法之外,还有分层网络算法[19]、最大流算法以及基于量子协同的智能优化算法[20]等.在DNA计算产生之后，2002年高琳等人[21]提出了一种基于质粒DNA的计算模型,并将其用于求解二部图的匹配问题.同年Wang[22]提出了一种用于求解二部图最大匹配的DNA算法.2003年董亚非[23]利用肽核酸(PNA)提出粘贴模型的完美匹配问题的分子算法.该算法首先将问题映射到DNA存储链，利用PNA分子在无盐状态下比DNA分子更容易与DNA分子结合并稳定存在的特性，设计编码DNA存储链的补链(PNA粘贴链),以达到计算的目的.2011年，周旭等人[24]给出了一种最大匹配问题的DNA计算算法，该方法在保持多项式操作时间的条件下，将解空间从O(2m)减少到O(1.618m).

本文则是利用DNA自组装模型的高度并行性,结合二部图本身的特征,建立了一种用于求解二部图完美匹配的一种自组装计算模型,对任意二部图只需14种Tile类型就能够得到完美匹配.

1 DNA计算自组装模型

文献[14-16]中对自组装模型的定义及相关符号描述如下：

定义1. 一个DNA计算自组装系统S是一个3元组〈T,g,τ〉，其中T为DNA Tile集合，g为结合强度函数，τ为热力学温度.

DNA Tile是带有4个粘性末端的分子元件，它可以和带有与其互补的粘性末端的DNA Tile相结合，形成规模庞大的带有唯一结果的二维结构.一个Tile是一个四元组〈σN,σE,σS,σW〉∈Σ4,这里Σ是具有粘性末端集合.Σ是一个有限的字母(结合域)集合，包括空集null，如果没有特别指出，empty=〈null,null,null,null〉是一个特殊的Tile，表示不与任何Tile相结合的Tile.

结合强度函数g:Σ×Σ→，∀σ∈Σ,g(null,σ)=0,表示粘贴域强度为0.

对于方向集D={N,E,S,W}来讲，对于所有点的坐标(x,y)∈2,都有N(x,y)=(x,y+1),E(x,y)=(x+1,y),S(x,y)=(x,y-1),和W(x,y)=(x-1,y).如果∃d∈D，使d(x,y)=(x′,y′),那么就说位置(x,y)和位置(x′,y′)相邻.对于一个Tilet,d∈D,则用bdd(t)表示Tilet在边d上的结合域.

若T是一个包含emptyTile的一个集合，A:×→T是T的一个配置.A是有限的，即A(x,y)≠empty,(x,y)∈T.A(x,y)=t表示Tilet在位置(x,y)处与配置A结合.

定义2. 在一个Tile系统中，A是部分Tile集T⊆Σ4的一个配置，那么要使Tilet∈T能够在位置(x,y)上结合到A上，从而产生一个新的配置A′，必须满足4个条件：

1) (x,y)∈A;

2)Σd∈Dg(bdd(t),bdd-1(A(d(x,y))))>τ且d-1表示和d在方向上对应的边;

3) ∀(u,v)∈2,(u,v)≠(x,y)⟹A′(u,v)=A(u,v);

4)A(x,y)=t.

即要使一个Tile能够稳定结合到一个配置上，当且仅当它与相邻的Tile的结合域强度之和大于或等于热力学温度τ.对所有结合域σ,g(σ,σ)=1,τ=2，那么一个Tilet要想结合到某位置上，它至少要和2个Tile结合.

定义3. 在一个Tile系统S中,A是Tile集T′⊆Σ4的一个配置，那么一个Tilet∈T能在位置(x,y)上从配置A上分离下来并产生一个新的配置A′，当且仅当其满足4个条件:

1) (x,y)∈A;

2)Σd∈Dg(bdd(t),bdd-1(A(d(x,y))))<τ;

3) ∀(u,v)∈2,(u,v)≠(x,y)⟹A′(u,v)=A(u,v);

4) (x,y)∉A′.

即当一个Tile和与它相邻Tile的结合域强度之和小于热力学温度τ，它就能从所在配置上分离下来.例如，对所有的σ，g(σ,σ)=1并且τ=2，如果少于2个Tile在与Tilet相邻的位置与之结合，那么Tilet就会从其位置上分离下来.

经过连续不断的组装后得到的最后结果，称为最终配置.如果在所有操作下得到的最终配置相同，则称系统产生唯一的最终配置.

2 求解完美匹配问题的DNA自组装计算模型

2.1 完美匹配问题

在无向图G=(V,E)中，边集E的任意一个子集M⊆E，若M中的任意2条边都没有公共端点，则称M为图G的一个匹配.若匹配M中的所有与匹配边相关联的顶点称为关于M饱和点，否则称为M非饱和点[24].

M是二部图G中任意一个匹配，若G的任意一个互补点集V1和V2中的所有点都是M饱和点，则M就是一个完美匹配[24-26].如图1所示，G是一个具有10个顶点的二部图.其中M1={e1,e4,e8,e11,e12},M2={e1,e5,e7,e11,e12}都是图G的完美匹配.

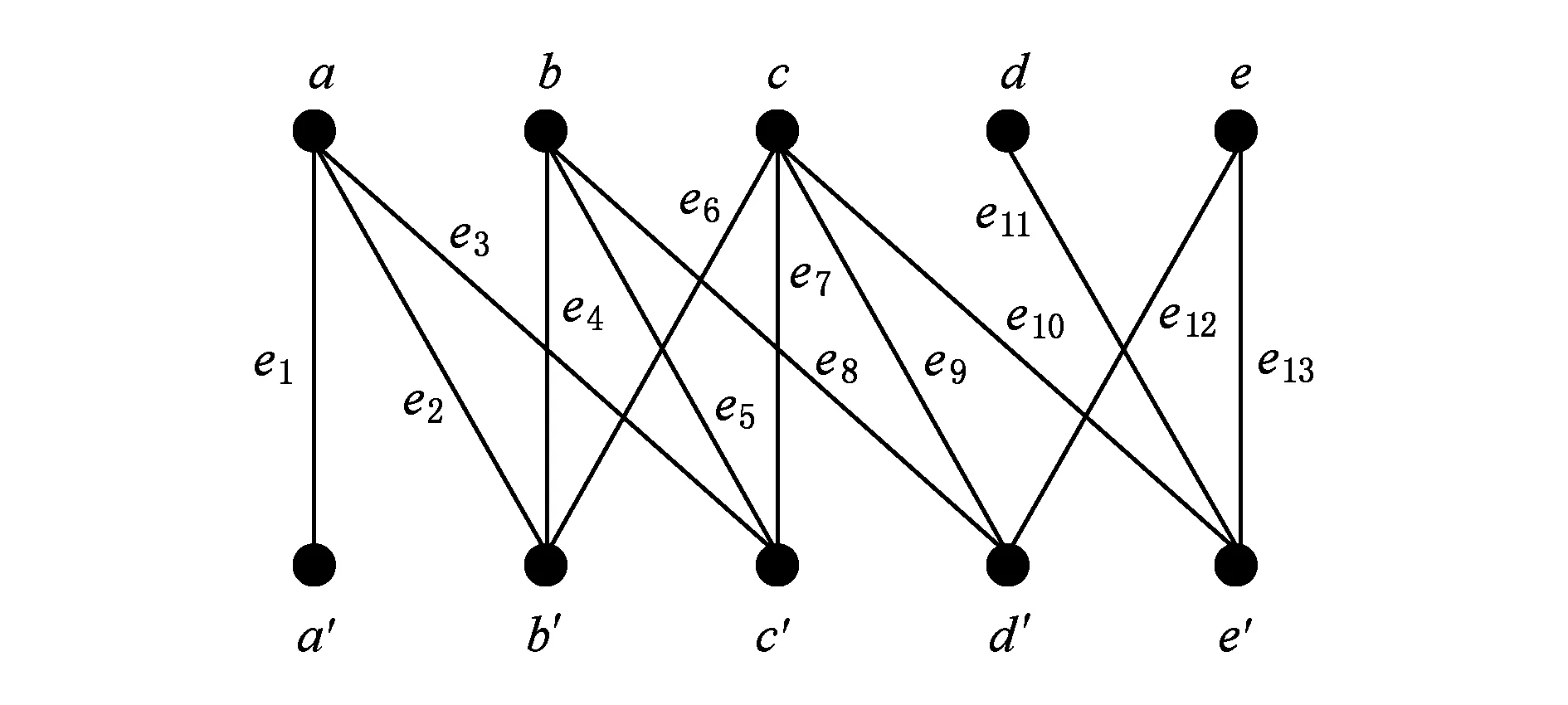
Fig. 1 Bipartite graph G.图1 二部图G

2.2 算法模型实例

本文结合完美匹配的概念及图中各顶点间的邻接关系，给出了一个基于DNA计算自组装模型的系统，并为该系统设计编码DNA Tile以及种子配置.在这个系统中，DAN Tile在一定的控制条件下执行自组装运算，整个运算过程从种子配置开始自右向左、自下向上进行，最终将会计算出一个组装体.若自组装得到的结果是完美匹配，将会在模块的左上角出现一个Success标志的DNA Tile，否则模块将会在下一步的升温过程中溶解掉.

本文将这个系统定义为完美匹配自组装系统Spm=〈Tpm,gpm,τpm〉,其中：Tpm为自组装模型获得完美匹配所使用的所有Tile的集合;gpm是Spm的结合函数，Spm的结合域为Σpm={null,χ,r,-,=,v}，χ={a,b,c,d,e,a′,b′,c′,d′,e′}.结合函数定义如下：

1) ∀σ∈Σpm,gpm(σ,null)=gpm(null,σ)=0;

2) ∀σ∈Σpm{null,=,v},gpm(σ,σ)=1;

3)gpm(v,v)=2;

4)gpm(=,=)=2;

5) ∀σ,σ′∈Σpm, ifσ≠σ′, thengpm(σ,σ′)=0.

任意结合域与null的结合强度为0.除结合域=,v外,其余结合域与其自身的结合强度都为1.=,v与其自身结合强度为2.任何结合域与非自身结合域的结合强度为0.设定系统温度τ=2，也就是说只有当一个Tile的结合域强度之和大于或等于2时，它才能稳定地结合到已有的集合上.

2.3 DNA Tile编码设计

根据上述算法及完美匹配概念，本文对完美匹配自组装系统中的DNA Tile的编码设计如图2所示：

Fig. 2 Compute Tile.图2 运算Tile

图2(a)～(g)所示为完美匹配自组装系统Spm的所有组装都必须用到边界Tile.

图2(a)中的StartTile是组装开始的标志，自组装计算从StartTile开始向左执行.由图2(a)可知Start=〈v,null,v,-〉，即只有满足bdS(t)=v,bdN(t)=v,或bdE(t)=-(其中-表示Tile的结合域)的Tile才能与之结合.图2(b)中的Tile记为EndTile是第1行组装完成的标志，它控制自组装计算的方向，使其只能向上增长.End=〈r,-,r,null〉，只有满足bdS(t)=r,bdN(t)=r,或bdW(t)=-的Tile才能与之结合.图2(c)和图2(d)中的Tile都是辅助Tile，都在种子配置第0行.前者位于最右端，其北边与StartTile结合，后者位于最左端，与EndTile相结合.图2(e)中的Tile记为SuccessTile,是自组装结束的标志，也是组装成功的标志.当自组装得到的是正确的完美匹配时，将会在组装体的左上角出现一个成功标志，即SuccessTile.由图2可知，Success=〈null,=,r,null〉,bdN(R)=null,bdE(R)==(第2个=表示结合域),bdS(R)=r,bdW(R)=null,其西边和北边的结合域均为null，因此它可使得自组装运算不能继续向上和向左执行，从而结束整个组装过程.

图2(f)中的Tile记为RTile,是自组装最后一步的开始标志，它只能在S向与Z′ Tile(图2(h))相结合.由于bdN(R)=null，所以RTile的北边不能与任何Tile相结合，从而控制整个组织运算过程不能继续向上执行.图2(g)中的Tile记为LTile,L=〈r,r,r,null〉，是标志每行自组装运算结束的Tile.由于bdW(L)=null，所以没有Tile能够在其西边与之结合，从而控制每行自组装运算使其不能继续向左执行.

本文对完美匹配自组装系统Spm中运算Tile的编码设计如图2(h)～(n)所示.其中，图2(h)中的Z′ Tile是控制每行自组装运算向左执行的右边界运算Tile，它的S和N可与其他Z′ Tile或RTile相结合构成种子配置的第0列.图2(i)中的Tile记为κ=〈κ,null,null,null〉,是按顶点度数大小从右向左排列形成种子系统第0行的Tile，它的N与图2(n)中满足条件的运算Tile的S相结合.图2(j)中的X′ Tile是上边界Tile，是标志每一列自组装运算终止的Tile，也是用于读取完美匹配结果的Tile.其中，X′ Tile体上的X′ 是指当前列的顶点信息.

图2(k)中Tile 〈X′,r,X′,r,〉的作用是传递信息.X′将当前列的顶点信息向上传递，r将前面已经出现OKTile(图2(m))的信息向左传递.图2(l)中的 Tile 〈Y′,X′,Y′,X′〉，当bdS(t)≠bdE(t)时，X′和Y′分别将当前行和当前列的顶点信息向左和向上传递.图2(m)中的TileOK=〈X′,X′,X′,r〉，当bdS(t)=bdE(t)时，西边的r将已有OKTile的信息向左传递，同时其北边X′ 将当前列的顶点信息向上传递.图2(n)所示Tileδ=〈δ,-,κ,-〉.对∀i∈1,2,…,n/2,κi,δi∈χ，其中，κi是种子系统第0行第i列的Tile信息，枚举了种子系统第0行中所有的Tile的信息(种子系统中所有Tile的N的结合域).δi枚举了所有能与κiTile相结合的Tile的信息.κ是由κi组成的集合，δ是由δi组成的集合.不同的δTile间可以在E和W相互结合.

2.4 运算Tile的设计算法

根据2.1节可知，二部图的完美匹配作为一种特殊的匹配方式，它具有3个基本要求：1)必须包含图中所有顶点; 2)完美匹配中的任意2条边都不能有公共顶点(任意2条边都不相邻); 3)完美匹配中每条边的2个端点必须分别属于二部图的2个互补点集.根据以上3点可知，若图中存在1度顶点，那么与这个1度顶点相关联的边有且只有这一条包含在完美匹配中.所以为了简化求解的复杂性，本文在编码设计DNA Tile前，首先找出所有子图中的1度顶点、1度顶点的邻接点及与它们相关联的边，并根据这种关系设计编码对应的顶点Tile.具体算法如BigraphToTile(G,E,V)所示，其中V和E是图G的顶点集和边集.

算法1.BigraphToTile(G).

S←正偶数集合；

（1）焊接主梁桁架的上弦杆（采用¢48钢管），上弦杆水平接头处内穿长800mm的无缝钢管，左右分别搭接400mm，上弦杆与无缝钢管焊接牢固。

G=(V,E)；

TILE←∅；

if |V|∈S

while (V′≠∅)

ifv∈V′

TILE←TILE∪{Tv,Tv-1}；

designTv和Tv-1使得bdN(v)=bdS(v-1)；

E←E-{Ev,Ev-1}；

end if

G=(V,E)；

BigraphToTile(G)；

end while

while (V′=∅且V(G)=∅)

ifv∈V且v≠∅

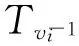
end if

end while

end if

returnTILE.

算法1中，G表示代求解的图，V和E分别为G的顶点集合和边集;V′ 表示图G中所有1度顶点构成的集合，v表示图G中的顶点，v-1为v相邻顶点;Tv表示所设计的关于顶点v的所有Tile构成的集合，Tv-1是关于顶点v-1所设计的所有Tile构成的集合,Ev表示与顶点v相关联的边集.TILE是所有1度顶点和非1度顶点的顶点Tile的集合.

如算法1所示，本文的DNA Tile编码设计步骤如下：首先找出原图G中1度顶点v构成的集合V′,若V′ 中存在1度顶点，那么设计DNA Tile使vTile只能与v-1Tile相结合;从原图删除顶点v和v-1，重置图G;重复上述操作，直到图G中顶点为0.若V′=∅，即图中没有1度顶点，则为G中的每对相邻的顶点设计顶点Tile，使G中每对相邻的顶点所对应Tile可以相互结合.

对于一个具有10个顶点的二部图(如图1所示)，其完美匹配自组装系统的种子配置如图3所示:

根据算法1，将5个顶点Tile按度数从小到大、从右向左排列，形成种子配置的第0行.剩下的5个顶点Tile构成自组装运算所需的Tile集T.同时将T中的所有Tile通过S和N的相互结合，由下至上排列形成种子系统第0列.

在τ=2的条件下，按照编码规则，在自组装的第1步结合上去的t∈T将会形成一个计算结果，本文将其称为结果序列.根据DNA自组装计算的高度并行性及海量的存储能力可知，若自组装运算数量足够大，最终一定能够得到完美匹配.但由于结合的随机性，结果序列中可能会出现重复的顶点Tile，很显然这种结果序列不是完美匹配.

为了将完美匹配从众多的结果序列中分离出来，本文同时在种子配置中设计了结果序列检测部分，检测结果序列中是否有重复的顶点Tile.若没有，说明结果序列是完美匹配，将在组装体左上角出现一个SuccessTile，从而分离出完美匹配；否则，组装体将在下一步升温过程中溶解.T中所有Tile的S和N相互结合，形成种子配置的第0列，即种子配置的结果序列检测部分.这里称结果序列检测部分的每个Tile叫检测Tile.

2.5 算法步骤

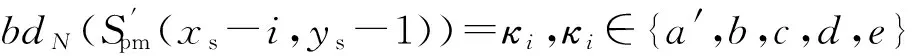
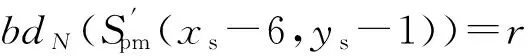
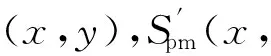
在τ=2的条件下，二部图G的完美匹配自组装过程如下：

Step1. ∀i=0,1,…,4，位置(xs-i,ys)∈Q1,bdW(S0(xs-i,ys))=-,bdN(S0(xs-i-1,ys-1))=κi.只有满足结合域为bdE(S0(xs-i,ys))=-,bdS(S0(xs-i,ys))=κi的Tilet,t∈U1,才能稳定地结合到S0上.在位置(xs-6,ys)∈Q1,bdW(S0(xs-5,ys))=-,bdN(S0(xs-6,ys-1))=r，U1中只有结合域bdS(t)=r,bdE(t)=r的EndTile满足条件.EndTile结合到配置上形成新的配置S1.Step1完成后，所产生的组装体如图4(a)所示.

Fig. 4 Perfect matching self-assembly model of the bipartite graph G shown in Fig.1.图4 图1二部图G的完美匹配自组装模型

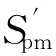
在此过程中，aTile一旦在结果序列中扫描到自身，将不会继续扫描，而是将信号r继续向左传递.在位置(xs-6,ys+1)上，因为bdW(S1(xs-5,ys+1))=r，bdN(S1(xs-6,ys))=r，故在t∈U2中，只有满足结合域为bdS(t)=r和bdE(t)=r的LTile才能稳定地结合到配置上，形成配置S2,如图4(b)所示.

Step3.重复Step2，分别对对应位置上b′ Tile，c′ Tile，d′ Tile和e′ Tile进行检测.检测结果如图4(c)～(f)所示.在检测完e′ Tile之后，形成配置S6，如图4(g)所示.

Step4. 完成自组装.由图4(g)可知，∀i=1,2,…,5，配置S6中的位置(xs-i,ys+6)∈Q7，暴露在外面的结合域为bdW(S6(xs-i+1,ys+6))==，bdN(S6(xs-i,ys+5))=κi.故在此步骤中，只有满足结合域bdS(t)=κi和bdE(t)==的Tile才能稳定地结合到配置上.当i=6时，即在位置(xs-6,ys+6)处，由于暴露在外面的结合域为bdW(S6(xs-5,ys+6))==，bdN(S6(xs-6,ys+5))=r，只有结合域为bdS(t)=r和bdE(t)==的SuccessTile才能稳定地结合到配置上，进而完成整个组装过程.如图4(h)所示.

记ti j∈Ui是能够在第i步中在位置(xs-j,ys-i)∈Qj处结合到配置Si上并能稳定存在的Tile，Δ=Σd∈Dg(bd(t),bdd-1(A(d(x,y))))≥τ是tTile能够稳定存在于配置上的条件.具体的自组装算法记为TileCompute(S0,n).

算法2.TileCompute(S0,n).

Sn←S0；

fori←0 ton

Sn←PerStep(Si-1,i)；

end for

ifSn(xs-n,ys+n)=Success

returnSn；

else

return failure；

end if

PerStep(Si-1,i)；

forj←0 tom

Si(xs-j,ys+i)=ti j；

end for

returnSi.

2.6 计算结果

本文提出的完美匹配自组装模型经2.5节的Step1自组装产生结果序列的过程中，对每个位置(x,y)∈Q1，U1中可能会有多个Tile能够结合到该位置上.而对于同一个Tilet,t∈U1，可能也能够结合到不同的位置(x,y)∈Q1上.也就是说位置(x,y)∈Q1和Tilet∈U1是多对一的关系.所以，在结果序列中可能会出现重复的顶点Tile，而这样的结果序列显然不是完美匹配.为了将完美匹配的结果序列与这些非完美匹配的结果序列分离开来，本文设计了结果序列检测部分.若结果序列是完美匹配，最终将在组装体的左上角出现一个标记Tile——SuccessTile；若不是完美匹配，组装体将在下一步升温过程中溶解，如图5(a)所示:

Fig. 5 Self-assembly model for perfect matching.图5 完美匹配自组装模型

图5(a)是种子配置经Step1自组装后形成的结果序列.由图5(a)可知，在结果序列中b′ Tile重复出现，而c′ Tile没有出现，显然这个结果序列不是完美匹配.图5(b)是种子配置的检测部分对结果序列进行检测的自组装模型.

由图5(b)可知，在对c′ Tile进行检测时，由于没有在结果序列中扫描到自身，故bdW(c′)=c将会一直向左传递.在位置(xs-6,ys+3)上，暴露在W和N的结合域bdW(S2(xs-5,ys+3))=c′，bdN(S2(xs-6,ys+2))=r，而U3中没有结合域为bdS(t)=r和bdE(t)=c′的Tile能够结合到该位置上，从而终止自组装运算.检测完成后，使τ=3.由结合函数的定义可知∀σ∈Σpm{null,=,v},gpm(σ,σ)=1.根据定义3可知，在τ=3的条件下，TileS2(xs-5,ys+3)会从组装体上分离下来.同样地，其他Tile最终也将分离下来，从而使整个组装体溶解掉.

3 算法分析

本文根据完美匹配概念及图中顶点间的邻接关系，编码完美匹配自组装系统用到的计算Tile.对于一个具有n个顶点的二部图来说，首先利用算法1根据图1中各顶点间的邻接关系，编码DNA Tile并形成种子系统.编码后的DNA Tile通过2.5节中的组装过程进行自组装.若组装成功，将在组装体左上角出现红色的SuccessTile；否则，组装体将在下一步升温过程中溶解.

定理1. 完美匹配自组装系统Spm=〈Tpm,gpm,τpm〉计算终止时返回的自组装结构是一个完美匹配.

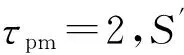
D0=〈X′,r,X′,r〉,

D1=〈Y′,X′,Y′,X′〉,

D2=〈X′,X′,X′,r〉,

D3=〈δ,-,κ,-〉,

D4=〈v,null,v,-〉,

D5=〈r,-,r,null〉,

D6=〈v,null,null,null〉,

D7=〈r,null,null,null〉,

D8=〈null,=,r,null〉,

D9=〈null,null,v,=〉,

D10=〈r,r,r,null〉,

D11=〈v,null,v,Z′〉,

D12=〈κ,null,null,null〉,

D13=〈null,=,X′,=〉.

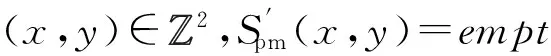
由2.4节可知：1)种子系统中第0行的D12与第0列的D11(或者D3Tile)是二部图中的顶点Tile，且两者交集为空;2)只有当D3Tile与D12Tile所代表的顶点相邻，D3Tile和D12Tile才能在自组装运算中稳定结合.由1)和2)和完美匹配的3个基本要求可知，若自组装计算2.5节的Step1完成后形成结果序列中没有重复的顶点Tile，则这个自组装结果就是一个完美匹配.在该系统中，除Step1之外，其余所有步骤都是在检测Step1产生的结果中没有重复序列.

接下来证明检测步骤中能够把不成功的计算结果检测出来而不被留在最终计算结果里.

对于任意含有重复Tile的S1,根据2.4节描述的检测过程中 ，∀i∈{1,2,…,k-1},i表示S1的横坐标，结合到位置(-i,d-1)上的S1是D1Tile.当i=k时，对于位置(-k,d-1)，只有E的结合域是Zd-1、S的结合域为r的Tilet才能稳定地结合上去，但Γ+中没有满足条件的Tilet.若假设在位置(-k+1,d-1)处的Tile为Tilet′，那么根据2.2节中gpm的定义，此时Tilet′的结合域强度和为2(E结合域强度为1，S结合域强度为1，N和W的结合域强度为0).在自组装运算过程中，系统温度τpm=2. Tilet′能够稳定结合在配置Sd上，但当系统温度升高到τpm=3时，根据定义3可知Tilet′将会从Sd上分离下来.

证毕.

定理2. 完美匹配自组装系统Spm=〈Tpm,gpm,τpm〉的组装时间是O(n)的.

∀w∈W0,S1(w)∈Uw，

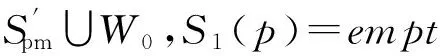
证毕.

定理3. 完美匹配自组装系统Spm=〈Tpm,gpm,τpm〉所需的Tile个数是Θ(n2).

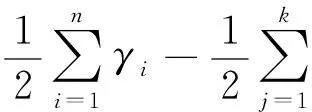
证毕.

4 结 论

本文针对二部图完美匹配问题提出了一种基于DNA计算自组装模型的算法.根据二部图完美匹配的概念及二部图中顶点间的邻接关系，设计编码DNA Tile及种子系统，并利用DNA计算自组装模型本身所具有的高度并行性、海量存储能力、低能耗和组装的自治性等特性，使运算DNA Tile在一定控制条件下执行自治的组装运算.

本文以一个具有10个顶点的二部图(如图1所示)为例,介绍了该算法的步骤：1) 给出DNA Tile的编码设计方案，该方案对所有子图中的 1度顶点t及与其相邻的顶点t-1进行编码，使tTile只能与t-1Tile相结合.由于这种处理方法避免了除t之外与t-1相邻的其他顶点的Tile的设计，故降低了DNA Tile的个数.同时，由于tTile是t-1Tile唯一能够结合的DNA Tile，所以在2.5节的Step1之后，生成的结果序列中没有其他DNA Tile与t-1Tile争夺与tTile结合的机会，从而提高了结果序列的准确率.另外，本文还设计了结果序列检测部分，通过对结果序列进行扫描，检测结果序列中是否存在重复的顶点Tile，从而判断结果序列是否是完美匹配.若不存在重复的顶点Tile，则说明结果序列是完美匹配，那么最终将会在组装体的左上角出现红色的SuccessTile，结果在组装体的最上面一行读取;否则，结果序列不是完美匹配.

在本系统中，在编码过程中的每一步都需要从子图G(V,E)中找出所有度数为1的顶点，并将1度顶点以及与1度顶点相邻的顶点和与它们相关联的边从图G中除去，并重置图G.

利用DNA自组装进行计算是一种新的计算理念，通过设计具有不同功能的DNA Tile，进而形成代表问题的解结构，从理论上展现了自组装模型应用于复杂问题的计算.

[1]Xu Jin, Bao Zheng. Neural networks and graph theory[J]. Scientia Sinica: Technologiea, 2001, 31(6): 533-555 (in Chinese)

(许进, 保铮. 神经网络与图论[J]. 中国科学: 技术科学, 2001, 31(6): 533-555)

[2]Azadeh A, Faiz Z S, Asadzadeh S M, et al. An integrated artificial neural network-computer simulation for optimization of complex tandem queue systems[J]. Mathematics and Computers in Simulation, 2011, 82(4): 666-678

[3]Liu Yang. Database processing in quantum computers[D]. Beijing: Tsinghua University, 2008 (in Chinese)

(刘洋. 量子计算机中的数据库处理[D]. 北京: 清华大学, 2008)

[4]Colnaghi T D, Ariano G M, Facchini S, et al. Quantum computation with programmable connections between gates[J]. Physics Letters A, 2012, 376(45): 2940-2943

[5]Rahman M O, Hussain A, Scavino E, et al. DNA computer based algorithm for recyclable waste paper segregation[J]. Applied Soft Computing, 2015, 31: 223-240

[6]Sun Y H, Chen M Y. A DNA-based solution to the graph isomorphism problem using Adleman-Lipton model with stickers[J]. Applied Mathematics and Computation, 2008, 197(2): 672-686

[7]Ouyang Q, Kaplan P D, Liu S, et al. DNA solution of the maximal clique problem[J]. Science, 1997, 278(17): 446-449

[8]Xu J, Qiang X, Yang Y, et al. An unenumerative DNA computing model for vertex coloring problem[J]. IEEE Trans on Nanobioscience, 2011, 10(2): 94-98

[9]Beneson Y, Tamar P, Adar R, et al. Programmable and autonomous computing machine made of biomolecules[J]. Nature, 2001, 414(22): 430-434

[10]Shi X, Chen C, Li X, et al. Size-controllable DNA nanoribbons assembled from three types of reusable brick single-strand DNA tiles[J]. Soft Matter, 2015, 11(43): 8484-8492

[11]Shi X, Lu W, Wang Z, et al. Programmable DNA tile self-assembly using a hierarchical sub-tile strategy[J]. Nanotechnology, 2014, 25(7): 075602

[12]Feynman R P. There’s plenty of room at the bottom[J]. Engineering and Science, 1960, 23(5): 22-36

[13]Adleman L. Molecular computation of solution to combinatorial problems[J]. Science, 1994, 266(5187): 1021-1024

[14]Winfree E. Algorithmic self-assembly of DNA[D]. Los Angeles: California Institute of Technology, 1998

[15]Zhang Xuncai. The research and applications of DNA computing by self-assembly[D]. Wuhan: Huazhong University of Science and Technology, 2009 (in Chinese)

(张勋才.自组装DNA计算模型的研究及应用[D]. 武汉: 华中科技大学, 2009)

[16]Chen Zhihua. Researches on several cryptological problems based on DNA computing by self-assembly[D]. Wuhan: Huazhong University of Science and Technology, 2009 (in Chinese)

(陈智华. 基于DNA计算自组装模型的若干密码问题研究[D]. 武汉: 华中科技大学, 2009)

[17]Brun Y. Solving satisfiability in the tile assembly model with a constant-size tiletset[J]. Journal of Algorithms, 2008, 63(4): 151-166

[18]Brun Y. Solving NP-complete problems in the tile assembly model[J]. Theoretical Computer Science, 2008, 395(1): 31-46

[19]Tang Min, Guan Jian, Deng Guoqiang, et al. A new algorithm and application of solving maximum matching problem of bipartite graph[J]. Computer Systems Applications, 2012, 21(3): 72-75 (in Chinese)

(唐敏, 关键, 邓国强, 等. 一种求解二部图最大匹配问题新算法及其应用[J]. 计算机系统应用, 2012, 21(3): 72-75)

[20]Ying Guisheng, Cui Xiaohui, Dong Hongbin, et al. Quantum-cooperative method for maximum weight perfect matching problem of bipartite graph[J]. Journal of Computer Research and Development, 2014, 51(11): 2573-2584 (in Chinese)

(印桂生, 崔晓晖, 董红斌, 等. 量子协同的二分图最大权完美匹配求解方法[J]. 计算机研究与发展, 2014, 51(11): 2573-2584)

[21]Gao Lin, Ma Runnian, Xu Jin. The molecular algorithm of the matching problem based on plasmid DNA[J]. Progress in Biochemistry and Biophysics, 2002, 29(5): 820-823 (in Chinese)

(高琳, 马润年, 许进. 基于质粒DNA匹配问题的分子算法[J]. 生物化学与生物物理进展, 2002, 29(5): 820-823)

[22]Wang Shiying. DNA computing of bipartite graphs for maximum matching[J]. Journal of Mathematical Chemistry, 2002, 31(3): 271-279

[23]Dong Yafei. The study of some DNA computing sticker models[D]. Wuhan: Huazhong University of Science and Technology, 2003 (in Chinese)

(董亚非. 若干DNA计算粘贴模型的研究[D]. 武汉: 华中科技大学, 2003)

[24]Zhou Xu, Li Kenli, Yue Guangxue, et al. A volume molecular solution for maximum matching problem on DNA-based computing[J]. Journal of Computer Research and Development, 2011, 48(11): 2147-2154 (in Chinese)

(周旭, 李肯利, 乐光学, 等. 一种最大匹配问题DNA计算算法[J]. 计算机研究与发展, 2011, 48(11): 2147-2154)

[25]Buckley F, Lewinter M. A Friendly Introduction to Graph Theory[M]. Upper Saddle River, NJ: Prentice Hall, 2005: 42-43

[26]Lü Zongwei, Lin Zhenghui, Zhang Lei. Boolean mapping algorithm based on perfect matching of bipartite graph[J]. Journal of Computer-Aide Design & Computer Graphics, 2001, 13(11): 961-965 (in Chinese)

(吕宗伟, 林争辉, 张镭. 基于二部图完美匹配的布尔匹配算法[J].计算机辅助设计与图形学学报, 2001, 13(11): 961-965)

Lan Wenfei, born in 1966. Master and professor. Her main research interests include databases, software technology.

Xing Zhibao, born in 1987. Master candidate. Her main research interests include DNA computing.

Huang Jun, born in 1991. Master candidate. His main research interests include DNA computing.

Qiang Xiaoli, born in 1979. PhD and associate professor. Her main research interests include molecular computing and bioinformatics.

The DNA Self-Assembly Computing Model for Solving Perfect Matching Problem of Bipartite Graph

Lan Wenfei, Xing Zhibao, Huang Jun, and Qiang Xiaoli

(CollegeofComputerScience,South-CentralUniversityforNationalities,Wuhan430074)

Biological systems are far more complex and robust than systems we can engineer today, and Because of its advantages of stability and specificity, DNA molecules have been used for the construction of nano-scale structures. With the development of DNA molecule self-assembly strategy, lots of programmable DNA tiles are constructed and used for solving NP problems. The tile assembly model, a formal model of crystal growth, is a highly distributed parallel model of nature’s self-assembly with the traits of highly distributed parallel, massive storage density and low power consumption. In the system, a function can be computed by deterministic assembly and identified two important quantities: the number of tile types and the assembly speed of the computation. Here a DNA self-assembly model for perfect matching problem of bipartite graph is demonstrated, and a 10-vertices bipartite graph is used as an example to illustrate this model. The computation is nondeterministic and each parallel assembly is executed in time linear in the input. The result shows that the successful solutions can be found among the many parallel assemblies, and it requires only a constant number of different tile types: 14.

perfect matching; bipartite graph; DNA computing; self-assembly; tile

2015-04-22；

2016-04-28

国家自然科学基金项目(61379059)；中央高校基本科研业务费专项基金项目(CZZ13003);2015年中南民族大学研究生优秀学位论文培育项目

强小利(qiangxl@mail.scuec.edu.cn)

TP301.6

This work was supported by the National Natural Science Foundation of China (61379059), the Fundamental Research Funds for the Central Universities (CZZ13003), and the Master Candidate Excellent Thesis Cultivation Project of South-Central University for Nationalities in 2015.