A Global Spectral Element Model for Poisson Equations and Advective Flow over a Sphere

Huan MEI,Faming WANG,Zhong ZENG,Zhouhua QIU,Linmao YIN,and Liang LI

1Institute of Oceanology,Chinese Academy of Sciences,Qingdao 266071

2Department of Engineering Mechanics,College of Aerospace Engineering,Chongqing University,Chongqing 400044

3Department of Chemical and Biological Engineering,Chalmers University of Technology,Gothenburg SE-412 96,Sweden

A Global Spectral Element Model for Poisson Equations and Advective Flow over a Sphere

Huan MEI∗1,Faming WANG1,Zhong ZENG2,Zhouhua QIU2,Linmao YIN2,and Liang LI3

1Institute of Oceanology,Chinese Academy of Sciences,Qingdao 266071

2Department of Engineering Mechanics,College of Aerospace Engineering,Chongqing University,Chongqing 400044

3Department of Chemical and Biological Engineering,Chalmers University of Technology,Gothenburg SE-412 96,Sweden

A global spherical Fourier–Legendre spectral element method is proposed to solve Poisson equations and advective flow over a sphere.In the meridional direction,Legendre polynomials are used and the region is divided into several elements.In order to avoid coordinate singularities at the north and south poles in the meridional direction,Legendre–Gauss–Radau points are chosen at the elements involving the two poles.Fourier polynomials are applied in the zonal direction for its periodicity, with only one element.Then,the partial differential equations are solved on the longitude–latitude meshes without coordinate transformation between sphericaland Cartesiancoordinates.Forverification of the proposed method,afew Poisson equations and advective flows are tested.Firstly,the method is found to be valid for test cases with smooth solution.The results of the Poisson equations demonstrate that the present method exhibits high accuracy and exponential convergence.Highprecision solutions are also obtained with near negligible numerical diffusion during the time evolution for advective flow with smooth shape.Secondly,the results of advective flow with non-smooth shape and deformational flow are also shown to be reasonable and effective.As a result,the present method is proved to be capable of solving flow through different types of elements,and thereby a desirable method with reliability and high accuracy for solving partial differential equations over a sphere.

spectral element method,spherical coordinates,Poisson equations,advective equation,Legendre–Gauss–Radau

1.Introduction

The global numerical model on a sphere is very important for its applications in geophysical areas,particularly the atmosphere.In computational fluid dynamics and geophysics, Poisson equations and advection are frequently applied,laying a foundation for solving time dependent incompressible fluid flow and describing the important transport processes that govern the important phenomena of atmosphere and ocean(Giraldo,1997;Qiu et al.,2012).For the fluid confined to a sphere,no boundary is adopted for the model. The key problems are mainly confined to the accuracy of the numerical method and coordinate singularities at the poles (Haidvogel et al.,1997).

Actually,coordinate singularities at the poles are due to the governing equations themselves being expressedin spherical coordinates.In polar coordinates,similar singularity occurs at the radius r=0 and has been widely studied for solving Poisson equations,e.g.,by spectral methods.In spectralmethods,two ways are usually adopted,i.e.,imposing pole conditions(Eisen et al.,1991;Huang and Sloan,1993;Matsushima and Marcus,1995;Shen,2000)and using Gaussian quadrature rules where the pole is not included in quadrature points(Chen et al.,2000).In spherical coordinates,some artificial pole conditions are also applied,and the governing equations are solved by various numerical methods(Lai and Wang,2002),e.g.,the finite difference method(Swarztrauber,1974)and finite volume method(Barros,1991).Obviously,pole singularities can be naturally avoided by solving the equations in Cartesian coordinates(Priestley,1992; Giraldo,1997,2000,2001).One frequently-used way of eliminating pole singularities is to adopt an icosahedral grid. Priestley(1992)employed the Taylor–Galerkin method on this type of grid;however,he executed an unnecessary step by mapping the 3D linear triangles to a 2D space,as reported by Giraldo(2001).Giraldo(1997,2000)solved the governing equations in a 3D space with linear triangular elements,where each triangle of the initial icosahedron is subdivided into several sub-triangles by a pth-order Lagrange polynomial.As a follow-up,Giraldo(2001)extended the previous work by replacing the linear triangular elements withhigh-order quadrilateral spectral elements,i.e.,comprising a spherical geodesic grids.Here,the initial triangle has to be mapped onto a gnomonic space,i.e.,coordinate transformation is required between Cartesian coordinates and spherical coordinates.Another common way of eliminating pole singularities is to apply rotation transformation where spherical geometries are tiled with rectangular elements or regions, which can be easily mapped from the sphere surface(from sphericalspacetognomonicspace).Ingeneral,thetilingprocess is accomplished by inscribing a polyhedron with rectangular faces inside the sphere and the polyhedron is always a cube.The governing equations are treated in Cartesian coordinates on the surfaces of such a cube.This approach has been employed by a number of researchers and combined with the spectral element method(SEM),either on structured grids(Haidvogel et al.,1997;Taylor et al.,1997;Fournier et al.,2004;Evansetal.,2010)orunstructuredgrids(Baeretal., 2006;Taylor and Fournier,2010).The same as icosahedral grids,an intermediate mapping has to be performed between the sphere and cube.In addition,the Yin–Yang grid is also an important mesh system,where most numerical algorithms based on longitude–latitude coordinates can be straightforwardly performed on this grid.However,inner boundaries exist in the Yin–Yang grid(Li et al.,2015).

©Institute of Atmospheric Physics/Chinese Academy of Sciences,and Science Press and Springer-Verlag Berlin Heidelberg 2016

For the global spherical model,spherical harmonics is the natural basic function and the spherical harmonics spectral method is mainly applied in climate models(Boer et al., 1992;Gates,1992).Inpreviouswork,Tayloretal.(1997)and Haidvogel et al.(1997)reported that the spherical harmonics spectral method showed high accuracy due to a completely isotropic representation of a scalar function on a sphere by the method.Although the global spectral method can achieve relatively high accuracy,the method is difficult to implement in parallel computation.Another challenge lies in local mesh refinement.For these reasons,the SEM can be a good alternative.The general advantage of the SEM is exponential convergence to the true solution,which occurs only for prefinement,and high accuracy can be achieved.The capabilities for problems in complex geometries and convenience of straightforward local mesh refinement enable the SEM to be appropriate for both atmospheric and oceanic problems. Also,the clustering points near poles can be avoided to relax the time step restriction(Taylor et al.,1997).Furthermore, the Message Passing Interface(MPI)parallel technique can be feasibly utilized for the SEM and parallel implementation is convenient for data exchange at the interface between two adjacent elements(Fournier et al.,2004;Giraldo and Rosmond,2004;Qiu et al.,2012).

Recently,Qiu et al.(2012)proposed a Fourier–Legendre spectral element method for solving Poisson equations and Navier–Stokes equations in polar coordinates.As a followup,Mei et al.(2013)introduced the method to simulations of the concentration homogenization process in hightemperature solution crystal growth with the accelerated crucible rotation technique.In the current paper,we extend the method to a spherical Fourier–Legendre spectral element methodforsolvingPoissonequationsandadvectiveflowover a sphere.Phillips(1957,1959)proposed a kind of composite grid to solve partial differential equations on a hemisphere,which is decomposed into two types of regions,and then used a Mercator map in low latitudes and a stereographic projection in high latitudes.In this paper,similar to Phillips’s method,the computational region is divided into two types of elements according to different latitudes:latitude bands in low latitudes and two polar caps in high latitudes.In the meridional direction,Legendre expansion is used.In order to avoid the coordinate singularities at the north and south poles,we adopt the Legendre–Gauss–Radau (LGR)quadrature points in the elements involving the two poles(polar caps)and Legendre–Gauss–Lobatto(LGL)in otherelements(latitudebands).Inthezonaldirection,Fourier expansion is employed due to its periodicity.As a result, a latitude–longitude mesh consisting of uniform and nonuniform spaced lines with respect to latitude and longitude is utilized,as shown in Fig.1a.Note that the two poles are included in the cap-elements without nodes;however,the integration of the partial differential equations has been performed over the poles.Herein,we place the emphasis on realizing such a SEM to solve Poisson equations and advective flow over a sphere.Since the LGR quadrature points are used for eliminating singularities,it is unnecessary to make a transformation between Cartesian coordinates and spherical coordinates.All unknown variables are solved in spherical coordinates based on the latitude–longitude grid,which is different from the SEM based on geodesic or cube–sphere meshes.In addition,the latitude–longitude grid can exploit its logically rectangular structure,orthogonality and symmetry to obtain all“eight properties”,as pointed out by Staniforth and Thuburn(2012).

The remainder of the paper is organized as follows:In section 2,the formulas of the Poisson equations and governing equations of advective flow are given.In section 3,the spherical Fourier–Legendre SEM is introduced and derived for solving the Poisson equations,as well as the corresponding SEM and temporal discretization for advective equations. Numerical results are discussed in section 4,followed by a short conclusion and further discussion in section 5.

2.Governing equations

2.1.Poisson equations

ThePoissonequationsonthesurfaceofaunitspherehave the form(Lai and Wang,2002)

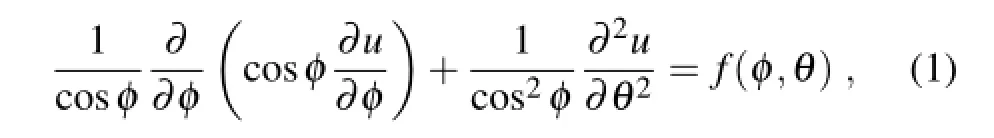
where the computational domain isφ∈[-π/2,π/2],θ∈[0,2π],φandθrepresent the latitude and longitude respectively,and f(φ,θ)must satisfy the compatibility condition to ensure the solution

2.2.Advective flow over a sphere

Advective flow within spherical geometries appears in many areas,such as geophysics,astrophysics and meteorology(Fornberg and Merrill,1997).Here,we consider a flow by solid body rotation over a sphere,where the velocity field is assumed to be constant.The governing equation of such flow is as follows(Williamson et al.,1992;Fornberg and Merrill,1997;Giraldo,1997):

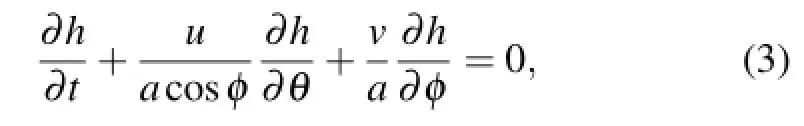
whereφandθrepresent the latitude and longitude respectively,a is the radius of the sphere,h is the height field,and (u,v)is the velocity field with respect to(θ,φ).

3.Numerical method

3.1.Spectral expansion

In this study,Fourier expansion and Legendre expansion are applied in the zonal and meridional directions,respectively.The Fourier and Legendre expansions of a 1D function can be written as

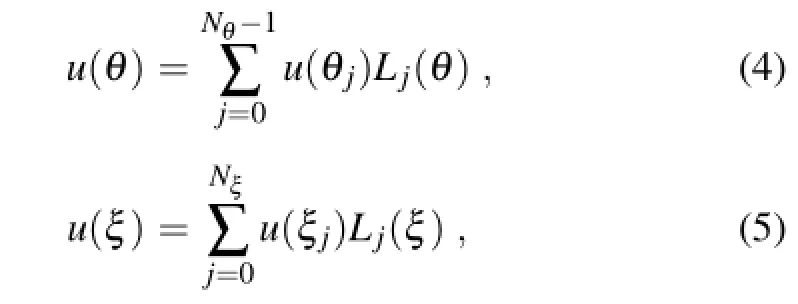
whereξj(j=0,...,Nξ)is the LGL or LGR quadrature point; θj=2πj/Nθ(j=0,...,Nθ-1);Nξand Nθare the degrees of Legendre and Fourier polynomials,respectively,with an even number Nθ;and Lj(ξ)and Lj(θ)are defined as the Lagrangian interpolation polynomials,with Lj(ξi)=δijand Lj(θi)=δij,whereδijis the Kronecker delta(Qiu et al., 2012).Accordingly,the matrix components of the collocation derivative are:

where QN(ξ)is the Legendre polynomial in the degree N,ωjis the quadrature weight function,andγk=(k+1/2)-1,k= 0,...,N.(Qiu et al.,2012).

3.2.Spherical Fourier-Legendre spectral element method for Poisson equations

To solve the partial differential equations using the SEM, the physical region Ω is divided into NE(i.e.the number of the elements)latitude bands and polar caps.As shown in Fig. 1b,the ith element Ωi:[φi,φi+1]×[0,2π]is displayed and mapped to the parent element[-1,1]×[0,2π]through the coordinate transformationξ=2(φ-φi)/(φi+1-φi)-1.All formulas and computations are derived from and performed on these normal elements.

A test function v is defined in the polynomial space VN. Multiplying Eq.(1)by the complex conjugate of v and integrating the equation by parts in the element Ωi,a Galerkin form is obtained for finding h∈H10(Ωi)(Iskandarani et al., 1995),

with differential formulas for the spherical element dΩ= cosφdφdθ.The functions u,v and f are discretized in Ωias the following forms:

Abbreviating ui(ξj,θk)to ujkand substituting Eq.(10) into Eq.(9),the resulting equation in the ith element Ωican be obtained from Eq.(9):

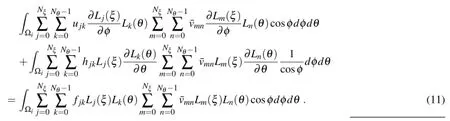
With the arbitrariness of{¯vmn},Eq.(11)becomes

In Eqs.(13)and(14),B[·,·]and f[·]represent the coefficients of the mass matrix and the right-hand side vector inΩi,respectively;Ajkmnand Bjkmnare:

Ajm,Bjm,Bjm,-1are defined and computed by the discrete quadrature as follows:

whereωjand Dpj,ξare the quadrature weight function and the matrix of the collocation derivative,respectively,depending on the LGR or LGL nodes.Here,the coordinate singularities arising in Eq.(19)for the elements at the poles are successfully avoided by using the LGR points.On the one hand, for the element including the north pole,the LGR quadrature pointsξj(j=0,...,N)are the zeroes of QN+1(ξ)-QN(ξ) withξ0andξN=1,where QN(ξ)is the Legendre polynomial in the degree N.On the other hand,the LGR quadrature pointsξj(j=0,...,N)are the zeroes of QN+1(ξ)+QN(ξ) withξ0=-1 andξNfor the element including the south pole. More detail can be found in Qiu et al.(2012)and Canuto et al.(1988).

Moreover,Aknand Bknare integrated directly as

As a result,the linear algebraic forms of Poisson equations for the ith element based on the spherical Fourier–Legendre SEM can be derived as

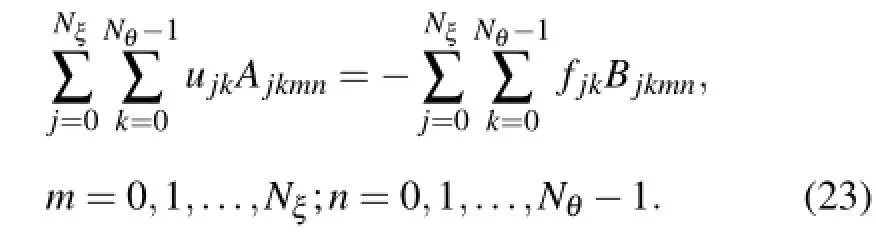
Subsequently,the global stiffness matrix is derived from the element stiffness matrices by referring to the finite element method(Wang,2003),and finally the values of variables for each node are obtained by solving the global linear equations. 3.3.Numerical method for advective flow

For the advective equation,the mesh and methodology are the same as for the Poisson equations.Multiplying Eq. (3)by a test function¯h defined in the polynomial space VNand integrating the equation in the element Ωi,we can obtain the integral form based on the differential formulas for the spherical element dΩ=cosφdφdθas follows:

where(u,v)is the known velocity field.Discretizing the functions h and¯h with the forms defined in Eq.(10),Eq. (24)becomes:

which is in a brief form with the arbitrariness of{¯hmn}as

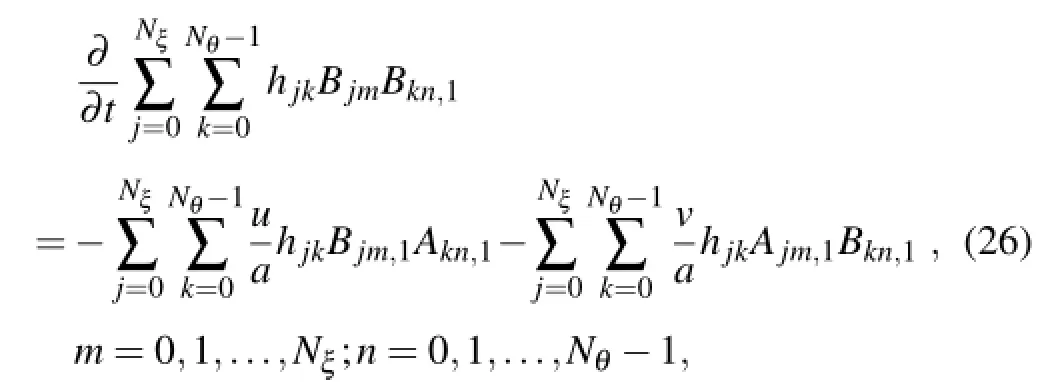
where Bjmis defined as in Eq.(18),and Ajm,1,Bjm,1,Akn,1and Bkn,1are defined and computed by discrete quadrature as follows:

where Dmj,ξis the matrix component of the collocation derivative with respect to the LGL or LGR quadrature points.

Thefourth-orderRunge–Kuttaexplicitschemeisselected for the temporal discretization.The detailed temporal discretization processes of the global form of Eq.(26)in Ω are described as follows:

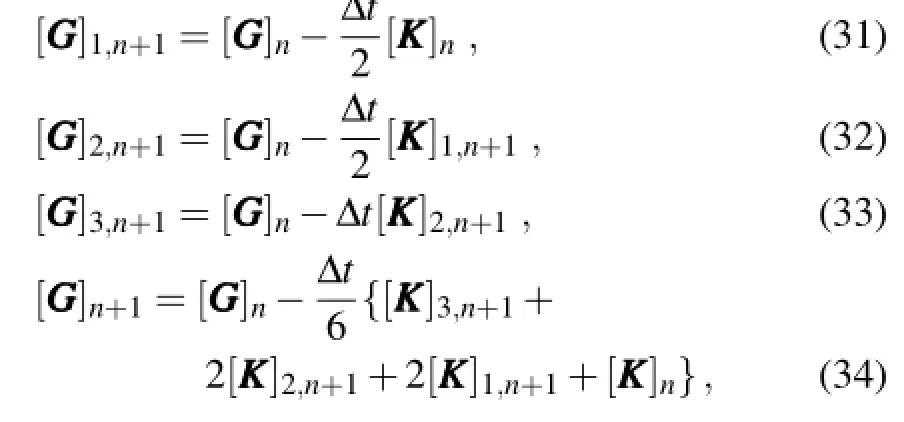
where Δt represents the time step;n refers to the time level t=nΔt;[ GGG]1,n+1,[ GGG]2,n+1,[ GGG]3,n+1(also for K)are the intermediate values;and the components of GGG and KKK are defined as

where NE represents the number of elements.As a result,the linear algebraic forms of Eqs.(31–34)on the global domainΩ can be derived based on the spherical Fourier–Legendre SEM at each intermediate step.Finally,the values of variables for each node are obtained by solving the linear equations.

4.Numerical experiments

4.1.Numerical error formulas

InthepresentSEM,thecomputationalareaisdividedinto NE elements in the meridional direction,while one single element exists in the zonal direction.Within each element the numbers of nodes are Nξ+1 and Nθin theφandθdirections,respectively.And the total number of nodes(ND)is ND=(NENξ+1)×Nθ.the absolute errors of The 2-norm (E2),the∞-norm(E∞),the average relative error(Erel,aver), the normalized e1,e2and e∞errors,emaxand eminerrors are adopted to evaluate the accuracy.The formulas of these errors are:

where hnumerand hexactrepresent the numerical and exact solutions of variable h,respectively;hi,numer(hi,exact)represents the value of hnumer(hexact)on the ith node;and Ω is the spherical surface.Δh0is the difference between the maximum and minimum values of the initial condition.

4.2.Results for Poisson equations

In this subsection,we firstly examine the numerical results of the Poisson equations,in comparison with the results of Lai and Wang(2002),where a class of FFT-based fast direct solvers are employed based on the finite difference discretization.We start with a Poisson equation with the exact solution u=cosφcosθ,where the right-hand side term is f=-2cosφcosθ,derived from Eq.(1).The meridional interval[-π/2,π/2]is divided into four sub-intervals for four elements:[-π/2,-π/4],[-π/4,0],[0,π/4]and[π/4,π/2]. The number of nodes is defined as Nθ=NE×Nξ,where NE is the number of elements in the meridional direction.In Table 1,the maximum errors and the corresponding meshes are obtained for the two methods.The accuracy of the present solution is improved by an increasing number of nodes.When Nξincreases up to 12(i.e.,49×48 meshes),the solution reaches the highest accuracy in the order of O(10-12).However,the accuracy gets slightly worse after the polynomial degree exceeds 12,which is probably caused by the accumulation of numerical errors(Qiu et al.,2012).The maximum errors obtained by Lai and Wang(2002)are O(10-5) and O(10-9)corresponding to the 2nd-and 4th-order methods upon 128×256 meshes,respectively.Thus,it can be remarked that the present SEM is capable of achieving high accuracy for Poisson equations with trigonometric polynomials.In order to better interpret that the highest accuracy is obtained at Nξ=12,we compute the order of convergence as an average convergence rate computed over all the grid refinements,where at each grid refinement,Nξ,the convergence rate is defined as Giraldo and Warburton(2005)

where e2,Nξrepresents the normalized e2error,while the order of the polynomial is Nξ.The convergence rates at different Nξare listed in Table 2,and the results show that bydoubling the grid the error is decreased by a factor of increasing convergence rate in the early stage(Nξ=1,2,4,8).Then, the convergence rate drops with Nξbetween 8 and 11;however,the accuracy of the numerical solution continues to increase as the rate is positive.The negative convergence rate meanstheaccuracyofthesolutionturnstodecrease.Through Eq.(45)it can be noted that the highest accuracy is obtained at Nξ=12,due to the positive rate at Nξ=11.Moreover,Nξis further increased up to 60,i.e.,241×240 mesh,and it is found that the rates are always negative(result not shown).

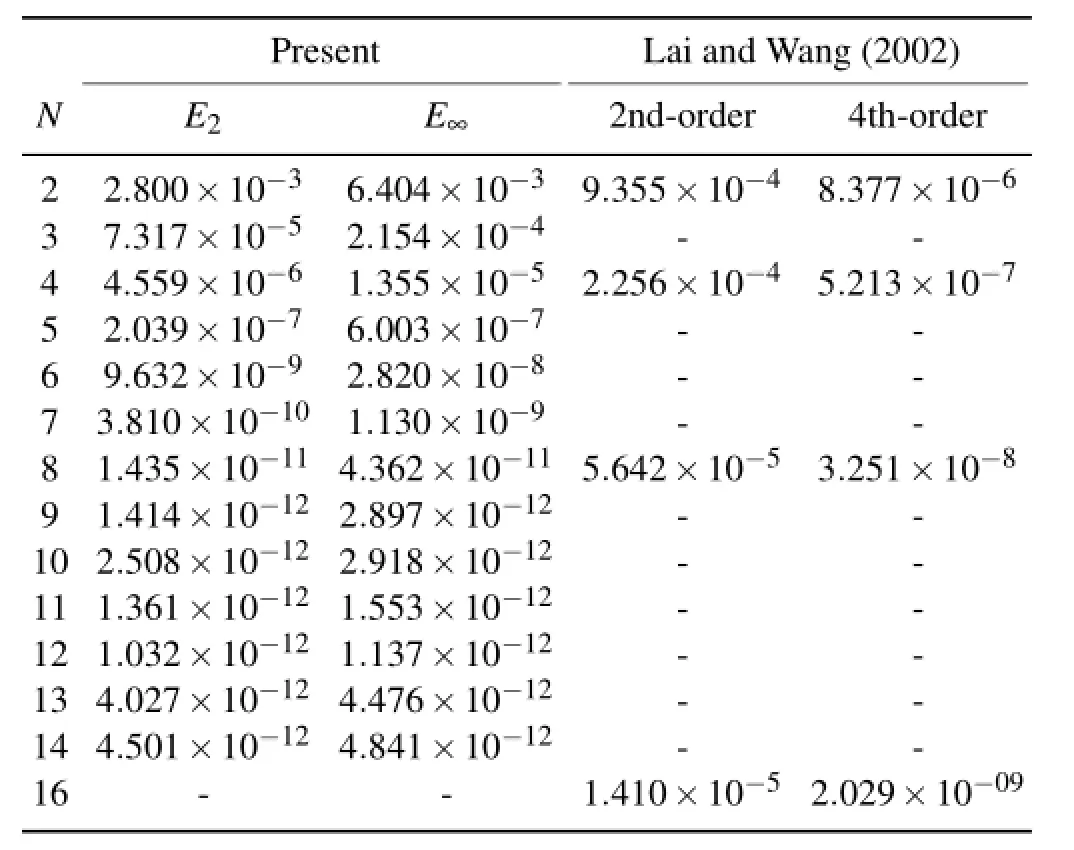
Table 1.Numerical errors for Poisson equations subjected to the exact solution u=cosφcosθwith N=Nξ.The number of grid points adopted in Lai and Wang(2002)is 8N×16N.The 2nd-order or 4th-order represents the order of the difference scheme,where the maximum error is listed below.

Table 2.The convergence rates at different Nξ.

We then consider two more complicated Poisson equations with the exact solutions u=cos4φ(0.5sin2θ-sinθcosθ)andu=sinφcos2φcos(2θ-3),respectively.Thecorresponding right-hand side terms can be derived from Eq.(1). The division of the meridional interval is similar as above. The number of nodes is Nθ=NENξ.The numerical errors for different pairs of(Nξ,Nθ)are computed and the smallest E2and E∞are determined.Table 3 lists the numerical errors for these two equations in comparison with the results of Lai and Wang(2002).It is shown that the present method gives higher accuracy.

Besides,two Helmholtz equations,Δu-u=f,with the exact solutions u=exp(sinφ)and u=exp(cosφcosθ), are computed.Relative to the Poisson equations,Helmholtz equations contain an extra term.So,the weak form of Helmholtz equations,as well as the resulting linear algebraic equations,is somewhat different from that of Poisson equations,though the detailed derivation process is similar to that for Poisson equations(Qiu et al.,2012).The element intervals are the same as those for the Poisson equations and the number of nodes is defined as Nθ=NENξ=NEN.As a result,we plot E2and E∞as a function of N in Fig.2.On the one hand,the solutions are obtained with an error magnitude in the order of O(10-12).The numerical solutions converge when N reaches 9 or 10.Similar to the Poisson equations, the accuracy again turns worse with an increasing polynomial degree.On the other hand,convergence of the SEM solution to the exact solution for fixed elements is achieved by increasing the polynomial degree.The error approaches zero exponentially fast with the polynomial degree for sufficiently smooth solutions,i.e.,exponential convergence.This exponential convergence occurs for p-refinement,which is contrary to the finite element h-refinement methods with algebraic convergence(increasing number of elements with polynomial degree fixed)(Fischer et al.,1988).

4.3.Results of advective flow with smooth shape

The following velocity field for the advection with smooth shape is considered:

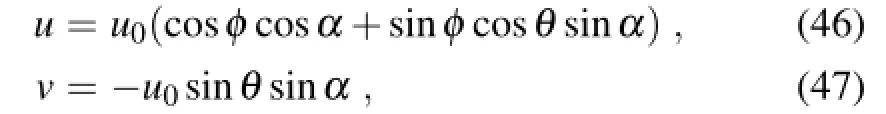
where u0=2πa/12days≈40 m s-1means that a full rotation takes about 12 days,andαis the angle between the rotational and the zonal directions.α=0 is adopted in this test.

Different from in the literature(Williamson et al.,1992; Fornberg and Merrill,1997;Giraldo,1997),a continuous initial condition is adopted,where h0=1000 m.At the moment t,the analytic solution has the form

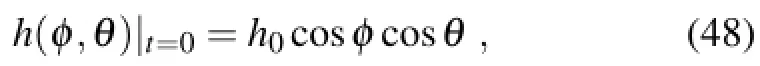
Table 3.Numerical errors for solutions of different Poisson equations with N=Nξ.The number of grid points adopted in Lai and Wang (2002)is 8N×16N.The 2nd-order or 4th-order represents the order of the difference scheme,where the maximum error is listed below.

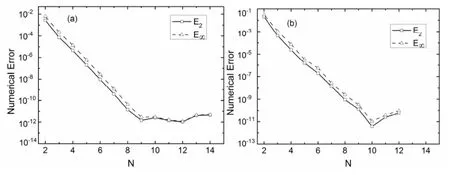
Fig.2.The plots of E2and E∞errors as a function of N for the Helmholtz equations with the exact solutions(a) u=exp(sinφ)and(b)u=exp(cosφcosθ).

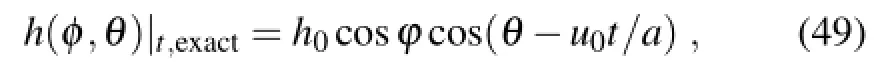
subjected to the solid body rotation,where a=6.37122×106m is the mean radius of the earth.

The 41×40 mesh with NE=4,Nξ=10,Nθ=40 is adopted for calculation(the mesh has converged;not shown). The meridional interval[-π/2,π/2]is divided into four sub-intervals for four elements,[-π/2,-π/4],[-π/4,0], [0,π/4]and[π/4,π/2].Prior to examining the results,the influence of the time step is estimated to minimize the temporal errors.Table 4 lists the average relative error of numerical solutions compared to exact solutions for different time steps after one full revolution.The results indicate that the numerical error decreases from 1.82×10-14to 1.75×10-14when the time step increases from 10 s to 100 s;however,the error increaseswhenfurtherincreasingthetimestep.Thetimestep of 100 s can thus be determined to be the optimal time step, which almost corresponds to the machine accuracy.Such a time step is also adopted for the following calculations,unless otherwise stated.

Figure 3 illustrates the numerical solution over time during one full revolution,where the vertical coordinate represents the value of variable h.In fact,h changes continuouslywith time,and each figure represents a phase position similar tothetrigonometricfunction,asshowninFig.3.InFig.3,the wave peak and wave trough change alternately with closely equal amplitude,and three days are nearly equivalent to a π/4 phase position in the trigonometric function.As stated by Fornberg and Merrill(1997),where the“cosine bell”was chosen as the initial condition,the numerical errors are distinct for the two finite difference methods due to numerical diffusion,compared with pseudo spectral methods.In order to confirm the underlying numerical accuracy,E2and E∞errors at different times are listed in Table 5 and the errors are in the order of O(10-11)-O(10-12).Furthermore,the errors almost remain stable during the time evolution,which demonstrates that the SEM is stable with little numerical diffusion for smooth problems.In addition,the e2norm of errors,which was used for accuracy evaluation in the work of Fornberg and Merrill(1997)and Giraldo,1997 for solving the advective equation,is also tested after one full revolution. The corresponding error norm even approaches the order of O(10-15)(not listed)–almost the machine accuracy.The results reveal that the present SEM is reliable for solving problems with smooth solutions.

Table 4.The average relative errors after one full revolution with different time steps for advective flow with smooth shape.

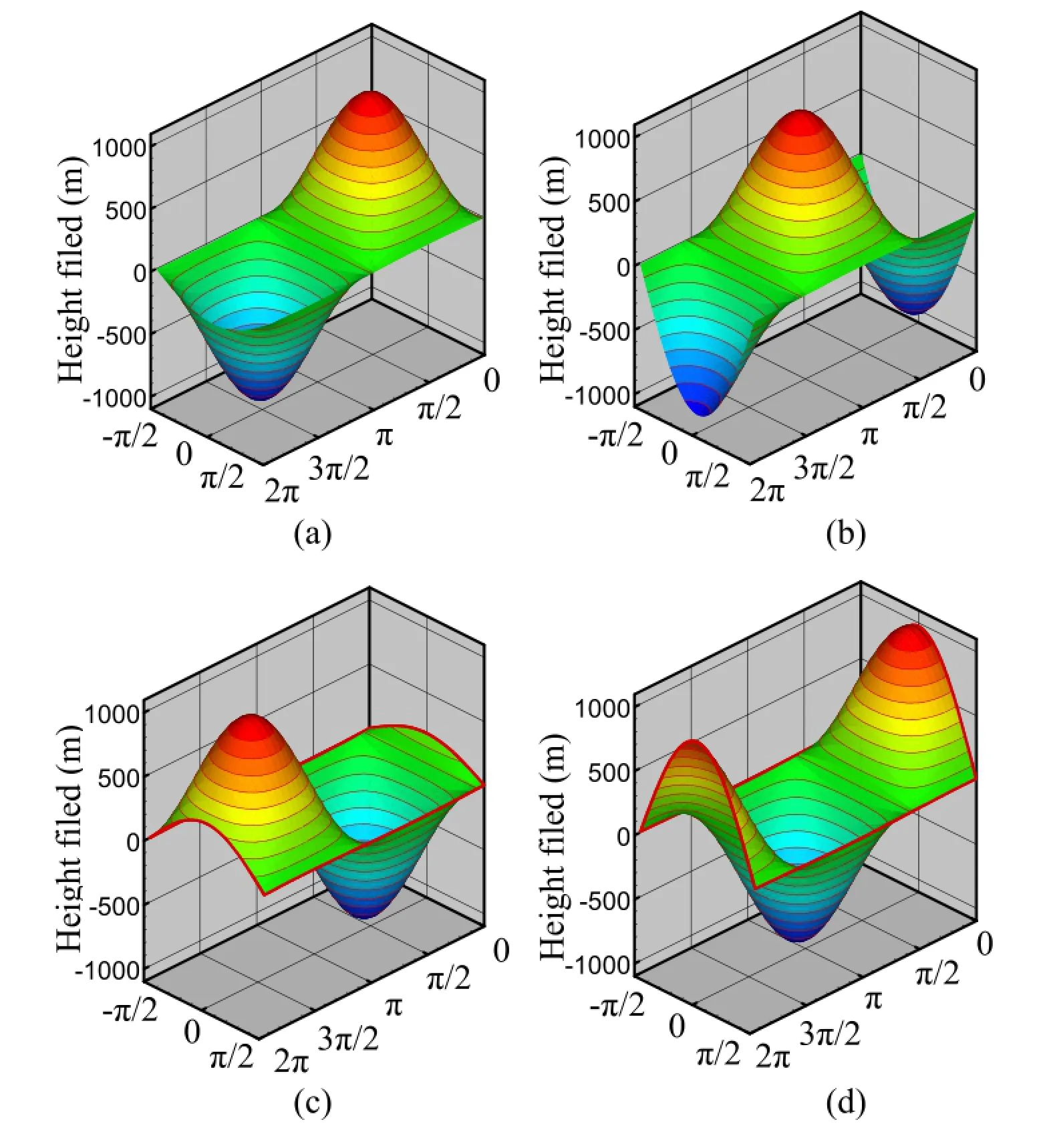
Fig.3.Numerical solutions(height field)of advective flow with smooth shape at different times within one full revolution:(a)3 days;(b)6 days;(c)9 days;(d)12 days.The vertical coordinate represents the value of variable h,and the horizontal coordinates represent the longitude and latitude,respectively.

Additionally,different variable values within one revolution and periodical variation at one point for a number of revolutions are exhibited and analyzed.Figure 4 shows the distributions of h along the large circleφ=0(θ∈[0,2π)) for different times in one revolution.We can see that all of the curves obey a cosine function with a phase difference of aboutπ/4 between the two adjacent times,as defined in Eq.(48).The wave peaks of h for four curves are nearlyunchanged in magnitude.This coincides with the physical meaning of the advective problem.In order to evaluate the error of the method for a longer computing time and further realize the periodical variation,an attempt is made to calculate the advective flow with smooth shape for more than one revolution.We can track h varying with time at the position (φ,θ)=(0,0),so that the numerical error can be evaluated for a long physical time.The total time is about 1200 days, which contains about 100 full revolutions.As shown in Fig. 5,the periodicity of the curve is distinct and homogeneous with little fluctuation in the wave peaks and wave troughs over all revolutions.Quantitatively,the magnitude of e2errors varies from 10-15to 10-13,which is likely caused by the accumulation of numerical errors due to the temporal iteration.However,this magnitude is still small and acceptable. In other words,for the spatially periodic problems,Fourier expansion can be utilized to ensure the periodicity and rationality.

Table 5.Numerical errors at different times with respect to Fig.3.

Fig.4.The distributions of h along the circleφ=0 andθ∈[0,2π)at different times for advective flow with smooth shape.

4.4.Results of advective flow with non-smooth shape

In this subsection,an advection test case described by Williamson et al.(1992)is adopted for validating the ability of the method handling non-smooth shape problems(i.e., advection of a cosine bell).The initial condition is given by

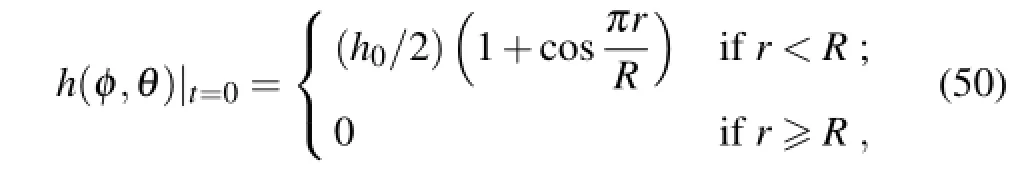
where h0=1000 m,R=a/3,and r is the great circle distance between(φ,θ)and the center.The initial position of the distribution center is located at(φc,θc)=(0,3π/2)(Williamson et al.,1992;Giraldo,1997):

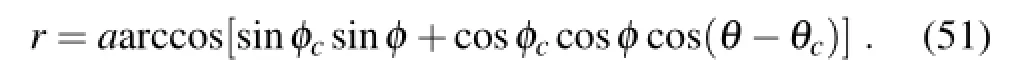
Firstly,the analytical velocity field is taken from Eqs.(46) and(47)forα=0.As with the advective flow with smooth shape,the 41×40 grid points with NE=4,Nξ=10,Nθ=40are adopted for calculation.As expected,the height field returns to its initial position while the solid rotation undergoes integral periods.

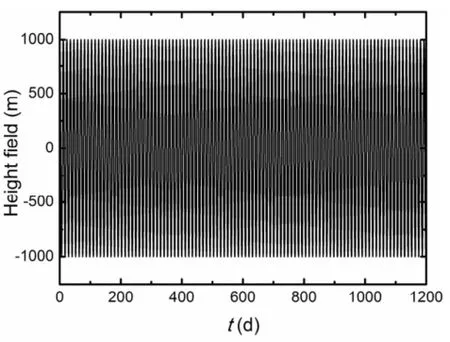
Fig.5.The value of h at（ the pos（ition(φ,θ)=(0,0),varying with time,for advective flow with smooth shape,where the total computation time is about 1200 days,which contains about 100 full revolutions.

The advection equation is solved for the height field for one full rotation(about 12 days).As for error analysis,the plots of contour lines on orthographic projection centered over the cosine bell and the normalized e1,e2and e∞are provided for qualitative and quantitative comparisons of the true solutions and numerical solutions,respectively.Figure 6 shows the contour lines on orthographic projection centered over the cosine bell of the true solutions(Fig.6a)and the spectral element solutions(Fig.6b)after one revolution from the viewpoint(φ,θ)=(0,3π/2)in spherical coordinates. The contour interval used in Fig.6 is 100 m without and with zero contours,respectively.Qualitatively,the numerical solutions coincide well with the analytic solutions.The normalized e1,e2and e∞are plotted as a function of time(days)in Fig.7.It is observed that the numerical errors oscillate near a small value with magnitudes of approximately 0.002 for e2and e∞,and 0.004 for e1.Although the oscillation amplitudes seem visible,the error ranges are comparable in magnitude to those observed in Taylor et al.(1997).In order to better understand the results,the slices of the contour plots along the longitudinal direction(keeping the latitude constant atφ=0) and the latitudinal direction(keeping the longitude constant atθ=3π/2)are given in Fig.8,with the curves passing through the center of the cosine bell(Giraldo,1997).Quantitatively,themaximumvaluesofsolutionsalongthetwoslices are both 1000,and the minimum values are-0.029 and 0,respectively.As a result,the spectral element solutions remain symmetric and are free from oscillation,consistent with the Lagrange–Galerkin solution obtained by Giraldo(1997).It is thus proved that the present method succeeds in solving such an advection with non-smooth shape.

Secondly,in order to verify the capability of the current method for solving flow through different types of elements, the advective equation withα=π/6 is also solved.In the calculation,it is found that the numerical results,especially the gradient of variables in the meridional direction when v/=0,greatly depend on the distribution of elements due to the non-smooth cosine bell.For the simulation of a problem with abrupt change in shape,the technique of domain decomposition is adopted to divide the region with a large variable gradient into several sub-regions,so as to alleviate the difficulty of the current method in simulation(Peyret, 2002).Here,the meridional region is divided into 26 elements(NE=26),and then the cosine bell covers at least two elements in the meridional direction.The 131×100 gird points(Nξ=5 and Nθ=100)and the time step Δt=50s are used in the simulation.The results ofα=0 andα=π/6 for one full rotation are compared quantitatively in Table 6.It can be seen from the e2errors that the accuracy of numerical results forα=0 is about one order of magnitude lower than that forα=π/6,as well as the minimum values of variable h.It is due to the fact that the large variable gradient of h and v/=0 induce relatively large numerical error in the meridional direction compared with the zonal direction.In spite of this,the refined distribution of elements based on the technique of domain decomposition gives an acceptable accuracy of numerical results forα=π/6.Fig.7.The normalized e1,e2and e∞errors of advective flow with non-smooth shape∞,shown as a function of time(day)for α=0.

Table 6.The results of non-smooth advection forα=0 andα= π/6.

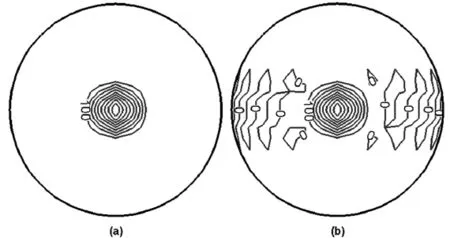
Fig.6.The contour lines on orthographic projection centered over the cosine bell of(a)true solutions and(b)spectral element solutions,after one revolution from the viewpoint(φ,θ)=(0,3π/2)for advective flow with non-smooth shape andα=0 in spherical coordinates,where the contour interval is 100 m without and with zero contours,respectively.

4.5.Results of deformational advective flow

A class of deformational flow tests on the sphere proposed by Nair and Lauritzen(2010)is resolved by the present method in this subsection.The magnitude of time dependent velocity vector monotonically decreases and reaches zero at half-time(T/2,where T is the duration of integration)and then increases with a sign change,resulting in a reversal of the flow field.Under this type of flow field,the extreme deformation of the initial height field occurs at t=T/2.Then, the height field goes back to its initial form at t=T.In this paper,we resolve the deformational flow adopting the advective form of Eq.(3),i.e.,Eq.(4)in Nair and Lauritzen(2010). For simplification,we assume that the radius a of the sphere is one.

Two symmetrically located cosine bells with zero background values(similar to the form of the single cosine bell in subsection 4.4)are used as initial height fields and defined as follows:

where i=1,2,hmax=1,r′=1/2,ri=ri(φ,θ)is the great circle distance between(φ,θ)and a specified center(φi,θi) of the cosine bell,which is given by

where the initial distributions(φi,θi)are chosen as(1) (φ1,θ1)=(0,5π/6)and(φ2,θ2)=(0,7π/6);and(2) (φ1,θ1)=(0,3π/4)and(φ2,θ2)=(0,5π/4)[Case-2 and Case-3 in Nair and Lauritzen(2010),respectively].

The wind fields of Case-2 and Case-3,which are nondivergent and divergent respectively,are defined as follows: Case-2:

Case-3:

Here,the parametersλ2=2 andλ3=1 govern the amplitude of the flow fields;and the duration of integration is T=5 non-dimensional units.

For the two cases above,we adopt a dense mesh for calculation(adopting polynomials of high degrees in both directions),where NE=4,Nξ=50,Nθ=200,i.e.,a 201×200 mesh.Both cases are run for 5000 time-steps(Δt=0.0001). As the height field returns to its initial form at the full integral time(T),the standard error norms for the SEM are given and compared with those of Nair and Lauritzen(2010), where the discontinuous Galerkin(DG)scheme and conservative semi-Lagrangian scheme(CSLAM)are used respectively,as shown in Table 7.It can be seen that the numerical errors for the two cases are acceptable and the present method achieves a slightly higher accuracy than the two methods in the reference for these two tests.Figures 9 and 10 show the initial conditions and the SEM numerical solutions for Case-2 and-3,respectively.The upper panels in Figs.9 and 10exhibit the initial wind fields and the initial h distributions, while the lower panels exhibit the SEM solutions at the half time(t=T/2)and the final time(t=T).Notably,the height field returns to its initial form after one full revolution.

Fig.8.The slices of the contour plots along the(a)longitudinal[keeping the latitude constant atφ=0, θ∈[0,2π)]and(b)latitudinal[keeping the longitude constant atθ=3π/2,φ∈[-π/2,π/2]]directions for advective flow with non-smooth shape andα=0,where the curves pass through the center of the cosine bell.

Table 7.Numerical errors for h for the deformational tests,Case-2 and Case-3,compared with those of Nair and Lauritzen(2010).

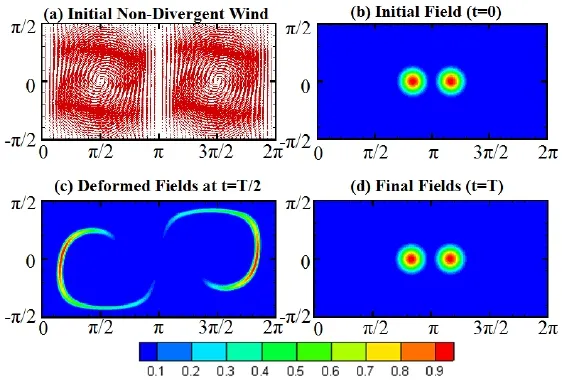
Fig.9.The non-divergent deformational flow test(Case-2).(a)Initial wind field.(b)Initial scalar field h(t=0)[two symmetrically located cosine bells with centers at d(0,5π/6)and(0,7π/6),respectively]. (c)Numerical solution for h at time t=T/2 units computed with the SEM.(d)Numerical solution for h at time t=T when the cosine bell patterns return back to their initial positions.

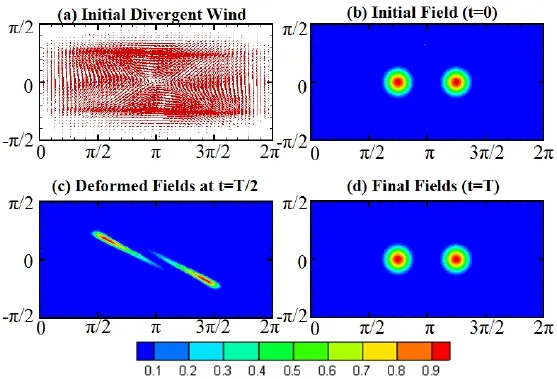
Fig.10.As in Fig.9 but for the divergent deformational flow field(Case-3)with two symmetrically located cosine bells with centers at(0,3π/4)and(0,5π/4),respectively.

5.Conclusion and discussion

In this study,the global spherical Fourier–Legendre SEM was described for solving Poisson equations and advective flow over a sphere.The coordinate singularities were eliminated efficiently by using the LGR points for the elements involving the poles.The longitude–latitude mesh was adopted and governing equations were solved in spherical coordinates.The transformation between Cartesian and spherical coordinates was omitted and it simplified the computational procedures.

Specifically,a few Poisson-type equations and advective equations were solved.The numerical results of the Poisson equations showed that the present SEM can achieve satisfactorily high accuracy,with error in the order of O(10-12). Exponential convergence was observed in the plots of the numerical errors.For time dependent problems,several advective flows with both smooth and non-smooth shapes and two deformational flows were investigated.The results obtained for smooth shape further verified the accuracy of the method for a continuous problem.It was found that the unknown variables vary periodically and the periodical curve is homogeneous through time revolutions,due to solid body rotation of the sphere.Furthermore,the results obtained for the nonsmooth shape were reasonable.For the deformational flow, the present method was also proved to be capable of solving this type of flow through different types of elements.In summary,the reliability and accuracy of the present SEM have been proved to be appropriate for the given partial differential equations over a sphere.

In order to enhance the applicability of the method in full dynamic problems,particularly those arising in the atmosphere,future work is suggested with the aim to extend the present method to full dynamical equations over a sphere, such as shallow water equations and the quasi-geostrophic equation.In addition,as summarized by Staniforth and Thuburn(2012),a global atmospheric model is determined by the combination of the grid and numerical method.For the choice of grid,which is essential,a quasi-uniform orthogonal quadrilateral grid is desirable.In this paper,the orthogonal quadrilateral grid is fulfilled for the spectral element grid. However,the spectral element method determines that the quadrature points are non-uniformly spaced.In spite of that, the high accuracy of the spectral element method may alleviate the method’s shortages to a certain extent,and dispersion analysis for the method would still be valuable in some special issues,as suggested by Staniforth and Thuburn(2012).

Acknowledgements.We wish to thank the two anonymous reviewers for their constructive comments and helpful suggestions. This work was supported by the Shandong Post-Doctoral Innovation Fund(Grant No.201303064),the Qingdao Post-Doctoral Application Research Project,the National Basic Research(973)Program of China(Grant No.2012CB417402 and 2010CB950402), and the National Natural Science Foundation of China(Grant No. 41176017).

REFERENCES

Baer,F.,H.J.Wang,J.J.Tribbia,and A.Fournier,2006:Climate modeling with spectral elements.Mon.Wea.Rev.,134,3610–3624.

Barros,S.R.M.,1991:Multigrid methods for two-and threedimensional Poisson-type equations on the sphere.J.Comput. Phys.,92,313–348.

Boer,G.J.,and Coauthors,1992:Some results from an intercomparison of the climates simulated by 14 atmospheric general circulation models.J.Geophys.Res.,97,12 771–12 786.

Canuto,C.,M.Y.Hussaini,A.Quarteroni,and T.A.Zang,1988: SpectralMethodsinFluidDynamics.1sted.,Springer Verlag, 32–70.

Chen,H.,Y.H.Su,and B.D.Shizgal,2000:A direct spectral collocation Poisson solver in polar and cylindrical coordinates. J.Comput.Phys.,160,453–469.

Eisen,H.,W.Heinrichs,and K.Witsch,1991:Spectral collocation methods and polar coordinate singularities.J.Comput.Phys., 96,241–257.

Evans,K.J.,M.A.Taylor,and J.B.Drake,2010:Accuracy analysis of a spectral element atmospheric model using a fully implicit solution framework.Mon.Wea.Rev.,138,3333–3341.

Fischer,P.,E.M.Ronquist,D.Dewey,and A.T.Patera,1988: Spectral element methods:Algorithms and architectures. Proc.1st Int.Conf.on Domain Decomposition Methods for Partial Differential Equations,Philadelphia,SIAM,173–197.

Fornberg,B.,and D.Merrill,1997:Comparison of finite difference-and pseudospectral methods for convective flow over a sphere.Geophys.Res.Lett.,24,3245–3248.

Fournier,A.,M.A.Taylor,and J.J.Tribbia,2004:The spectral element atmosphere model(SEAM):High-resolution parallel computation and localized resolution of regional dynamics. Mon.Wea.Rev.,132,726–748.

Gates,W.L.,1992:AMIP:The atmospheric model intercomparison project.Bull.Amer.Meteor.Soc.,73,1962–1970.

Giraldo,F.X.,1997:Lagrange-Galerkin methods on spherical geodesic grids.J.Comput.Phys.,136,197–213.

Giraldo,F.X.,2000:Lagrange-Galerkin methods on spherical geodesic grids:The shallow water equations.J.Comput. Phys.,160,336–368.

Giraldo,F.X.,2001:A spectral element shallow water model on spherical geodesic grids.International Journal for Numerical Methods in Fluids,35,869–901.

Giraldo,F.X.,and T.E.Rosmond,2004:A scalable spectral element Eulerian atmospheric model(SEE-AM)for NWP:Dynamical core tests.Mon.Wea.Rev.,132,133–153.

Giraldo,F.X.,and T.Warburton,2005:A nodal triangle-based spectral element method for the shallow water equations on the sphere.J.Comput.Phys.,207,129–150.

Haidvogel,D.B.,E.Curchitser,M.Iskandarani,R.Hughes,and M.Taylor,1997:Global modelling of the ocean and atmosphere using the spectral element method.Atmosphere-Ocean,35,505–531.

Huang,W.Z.,and D.M.Sloan,1993:Pole condition for singu-lar problems:The pseudospectral approximation.J.Comput. Phys.,107,254–261.

Iskandarani,M.,D.B.Haidvogel,and J.P.Boyd,1995:A staggered spectral element model with application to the oceanic shallow water equations.International Journal for Numerical Methods in Fluids,20,393–414.

Lai,M.C.,and W.C.Wang,2002:Fast direct solvers for Poisson equation on 2D polar and spherical geometries.Numerical Methods for Partial Differential Equations,18,56–68.

Li,X.H.,X.D.Peng,and X.L.Li,2015:An improved dynamic core for a non-hydrostatic model system on the Yin-Yang grid.Adv.Atmos.Sci.,32(5),648–658,doi:10.1007/s00376-014-4120-5.

Matsushima,T.,and P.S.Marcus,1995:A spectral method for polar coordinates.J.Comput.Phys.,120,365–374.

Mei,H.,Z.Zeng,Z.H.Qiu,L.Li,L.P.Yao,H.Mizuseki,and Y.Kawazoe,2013:Numerical simulation of crucible rotation in high-temperature solution growth method using a Fourier-Legendre spectral element method.International Journal of Heat and Mass Transfer,64,882–891.

Nair,R.D.,and P.H.Lauritzen,2010:A class of deformational flow test cases for linear transport problems on the sphere.J. Comput.Phys.,229,8868–8887.

Peyret,R.,2002:Spectral Methods for Incompressible Viscous Flow.Springer,New York,297–338.

Phillips,N.A.,1957:A map projection system suitable for largescale numerical weather prediction.J.Meteor.Soc.Japan, 75th Anniversary Volume,262–267.

Phillips,N.A.,1959:Numerical integration of the primitive equations on the hemisphere.Mon.Wea.Rev.,87,333–345.

Priestley,A.,1992:The Taylor-Galerkin method for the shallowwater equations on the sphere.Mon.Wea.Rev.,120,3003–3015.

Qiu,Z.H.,Z.Zeng,H.Mei,L.Li.,L.P.Yao,and L.Q.Zhang, 2012:A Fourier-Legendre spectral element method in polar coordinates.J.Comput.Phys.,231,666–675.

Shen,J.,2000:A new fast Chebyshev-Fourier algorithm for Poisson-type equations in polar geometries.Applied Numerical Mathematics,33,183–190.

Staniforth,A.,and J.Thuburn,2012:Horizontal grids for global weather and climate prediction models:A review.Quart.J. Roy.Meteor.Soc.,138,1–26.

Swarztrauber,P.N.,1974:The direct solution of the discrete Poisson equation on the surface of a sphere.J.Comput.Phys.,15, 46–54.

Taylor,M.A.,and A.Fournier,2010:A compatible and conservative spectral element method on unstructured grids.J.Comput.Phys.,229,5879–5895.

Taylor,M.,J.Tribbia,and M.Iskandarani,1997:The spectral element method for the shallow water equations on the sphere. J.Comput.Phys.,130,92–108.

Wang,X.C.,2003:Finite Element Method.Tsinghua University Press,73–74.(in Chinese)

Williamson,D.L.,J.B.Drake,J.J.Hack,R.Jakob,and P.N. Swarztrauber,1992:A standard test set for numerical approximationstotheshallowwaterequationsinsphericalgeometry. J.Comput.Phys.,102,211–224.

Mei,H.,F.M.Wang,Z.Zeng,Z.H.Qiu,L.M.Yin,and L.Li,2016:A global spectral element model for Poisson equations and advective flow over a sphere.Adv.Atmos.Sci.,33(3),377–390,

10.1007/s00376-015-5001-2.

8 January 2015;revised 13 July 2015;accepted 21 August 2015)

∗Huan MEI

Email:meihuan@qdio.ac.cn