触发器可靠度计算的F-PTM方法

欧阳城添,江建慧 ,王 曦

(1.同济大学软件学院,上海 201804; 2.江西理工大学信息工程学院,江西赣州 341000)



触发器可靠度计算的F-PTM方法

欧阳城添1,2,江建慧1,王 曦2

(1.同济大学软件学院,上海 201804; 2.江西理工大学信息工程学院,江西赣州 341000)

传统的概率转移矩阵(PTM)方法是一种用于估计软错误对组合电路可靠度影响的有效方法,但传统PTM方法只适用于组合逻辑电路的可靠度评估.触发器是时序逻辑电路的重要组成部分,其可靠度评估对时序电路的可靠度分析研究至关重要.为此,本文提出了基于PTM的触发器可靠度计算的F-PTM方法及电路PTM的判定定理.F-PTM方法首先建立触发器电路的特征方程,再用电路PTM的判定定理生成触发器的PTM,最后,根据输入信号的概率分布函数计算出电路的可靠度.与传统PTM方法相比较,F-PTM方法既能计算组合电路的PTM,又能计算触发器电路的PTM,其通用性强.对典型的触发器电路和74X系列电路中的触发器电路的实验结果表明,F-PTM方法合理可行.与多阶段方法和Monte Carlo方法的实验结果相比较,F-PTM方法得到的结果更精确.

软错误;触发器;可靠度评估;概率转移矩阵;半张量积

1 引言

随着深亚微米、纳米工艺在超大规模集成电路中的应用,高层次电路的可靠性评估日益成为人们关注的焦点[1～5].近年来提出的时序电路高层可靠性评估方法,主要分为两类:①评估时序电路的软错误率:基于符号模型的时序电路可靠性分析方法用于估计时序电路的软错误率[6,7];时序电路差错传播概率分析方法(Sequential Error Propagation Probability analysis,S-EPP)用于评估电路受粒子撞击时时序电路的差错锁存概率[8];②时序逻辑电路的可靠度计算:多阶段(Multiple-Pass,MP)可靠性评估方法通过电路的迭代方式评估时序逻辑电路的可靠性[9],是组合电路的单阶段(Single Pass,SP)可靠性评估方法[10,11]的扩展;基于贝叶斯网络(Bayesian Networks,BN)的时序电路可靠性分析方法通过贝叶斯网络分析工具计算电路的平均差错概率[12,13].

触发器的可靠性评估对时序电路可靠性分析至关重要.但上述时序电路可靠性评估方法对触发器的可靠性分析不够深入：①在BN方法中,假设时序电路中的触发器是理想电路[12,13],不会发生软错误.因此,该假设会影响可靠性评估结果的精度;②MP方法在分析触发器内部的反馈信号对电路的可靠度影响时,假设反馈信号对触发器电路的影响为一个梯度因子gr (gradient factor).但文献[9]中没有给出gr的取值依据,而是人为设定,这种取值方法会影响触发器电路可靠性评估结果的精度.

传统的基于概率转移矩阵(Probabilistic Transfer Matrix,PTM)的可靠性分析方法[14]首先建立门电路的PTM,然后根据电路结构和矩阵运算规则计算整个组合电路的PTM,再从电路的PTM中获得电路的可靠度信息.但传统的PTM方法是根据电路的串联和并联结构来计算组合电路的PTM.然而,触发器电路内部存在反馈,它不能表示为串尝联结构,所以传统PTM方法不适于触发器电路.为此,文献[15]提出了触发器的可靠度计算的初步想法,但还不完善与深入.

鉴于此,本文提出基于概率转移矩阵的触发器可靠度计算方法(Reliability Estimation of Flip-Flops Based on Probabilistic Transfer Matrix,F-PTM)和电路PTM的判定定理.F-PTM方法首先建立触发器电路的特征方程,再用电路PTM的判定定理推理计算触发器电路的PTM,最后,根据输入信号的概率分布函数计算出电路的可靠度.通过理论证明和实验验证了所提出评估方法的正确性与可行性.与传统的PTM方法相比较,本文提出的F-PTM方法既能计算组合电路的PTM,也能计算触发器电路的PTM,其通用性强,与已有的评估方法相比较,采用F-PTM方法得到的可靠性评估结果更精确.

2 触发器PTM的计算

2.1R-S锁存器PTM的计算

设构成R-S与非门锁存器的两个与非门为a和b,它们的PTM分别为Pnanda,Pnandb.如式(1)所示,其中,pax1x2表示给定输入i=x1x2时,与非门a输出错误结果的概率；1-pax1x2表示给定输入i=x1x2时,与非门a输出正确结果的概率.

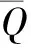
同样地,可以推算出RQS在其他状态时,Q输出0或1的概率,如表1所示.

表1 输入为RQS时,输出为Q的条件概率

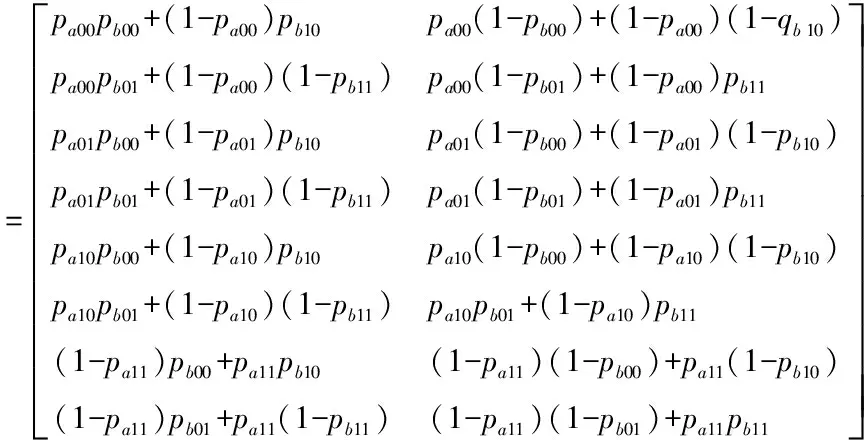
=(Pnanda⊗I2)*Pnandb

Prs-latch= (F2⊗F2⊗F2)*(I2⊗W2⊗I2)

其中I2表示一条连接线的ITM,F2表示2输出扇出的ITM,W2表示两条交叉连接线的ITM.

同理,推导出钟控R-S锁存器和D锁存器的PTM:

Prs-latch-c=(Inot⊗I2⊗Inot)*Prs-latch

Prs-latch= (F2⊗I2)*(I2⊗W2)*(I2⊗F2⊗Pnot)

*Prs-latch-c

2.2 电路PTM的判定定理

从上一节的研究可知,锁存器的PTM可以由PTM的半张量积运算得到.但推导过程繁琐,为此,提出定理1和定理2,称两个定理为电路PTM的判定定理.

定理1 设逻辑门g实现函数f(x1,x2,…,xk,…,xm);当输入向量为i=(x1x2…xk…xm)时,门g的输出概率分布向量为Og,i.那么,对于任意一个输入向量i=(x1x2…xk…xm),Pg是逻辑门g的PTM当且仅当等式(2)成立.

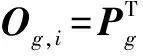
(2)

其中,Xm=[1-xmxm]T为逻辑变量xm的矩阵表示形式.

充分性证明

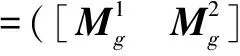
(3)

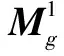
必要性证明

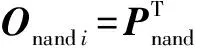
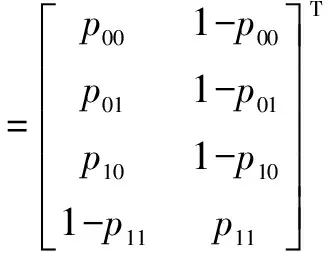
定理2 设电路C实现函数F(x1,x2,…,xk,…,xm);电路C的输出概率分布向量为Oc,i.那么,对于任意一个输入向量i=(x1x2…xk…xm),PF是电路C的PTM当且仅当等式(4)成立.

(4)

其中,Xm=[1-xmxm]T为逻辑变量xm的矩阵表示形式,

充分性证明

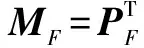
(5)

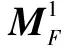
必要性证明

电路PTM计算的基本步骤归纳为:①电路用逻辑函数表示;②从电路的逻辑函数触发,根据定理1或定理2得到输入向量i=(x1x2…xk…xm)时,电路的输出概率分布向量为Oc,i的表达式;③推理和化简Oc,i表达式,把它化简成形如式(5)的规范型;④最后根据定理2可以判断PF为电路的PTM.

为了说明新的PTM方法计算电路PTM的计算过程,下面给出几个例子.

例2 设逻辑电路C是由两个串联的子电路C1和C2组成,如图2所示.子电路C1和C2的逻辑函数分别为Y=F1(x1,x2,…,xm)和Z=F2(y1,y2,…,yn).子电路C1和C2的PTM分别为P1和P2.

因为子电路C1的输出连接到子电路C2的输入,把等式Y=F1(x1,x2,…,xm)带入等式Z=F2(y1,y2,…,yn),并得到等式Z=F2(F1(x1,x2,…,xm)).那么,根据定理2可以得到：

因此,根据定理2可以判断：由两个串联的子电路C1和C2组成的逻辑电路C的PTM为Pc=P1*P2.从而证明传统PTM方法中两个串联电路计算PTM的公式.

例3 设逻辑电路C是由两个并联的子电路C1和C2组成,如图3所示.子电路C1和C2的逻辑函数分别为Y=F1(x1,x2,…,xm)和Z=F2(p1,p2,…,ps).子电路C1和C2的PTM分别为P1和P2.那么,根据定理2可以得到：

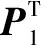
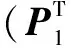
因此,根据定理2可以判断：由两个并联的子电路C1和C2组成的电路C的PTM为Pc=P2⊗P1.从而证明传统PTM方法中两个并联电路计算PTM的公式.

例4 基本R-S与非门锁存器电路如图1所示.设与非门的PTM是Pnand,基本R-S与非门锁存器的特征方程为Qn=(R↑Q)↑S.那么,根据定理1得到:

从上述例子可以表明,使用新PTM方法既可以计算组合电路的PTM,也可以计算触发器的PTM.其通用性更强.

2.3 触发器的PTM计算

根据定理1,2,可得边沿J-K触发器的PTM:

同理,可以推导出正边沿R-S触发器,正边沿D触发器,主从R-S触发器,主从J-K触发器和主从D触发器的PTM,分别为:

Prs-FF-e=(Inot⊗I2⊗Inot)*Prs-latch

PD-FF-e=(F2⊗I2)*(I2⊗W2)*(I2⊗F2⊗Pnot)*Prs-FF-e

PRS-FF-ms=(F2⊗I2)*(I2⊗W2)*(I2⊗F2⊗Pnot)*Prs-latch-c

PD-FF-ms=(I2⊗F2)*(PD-latch,Q⊗I2)*PD-latch

3 触发器可靠度的计算方法

3.1 触发器PTM的迭代计算

触发器电路可在时间上展开成一个重复的组合逻辑阵列,阵列中的每个组合电路对应一个时序帧,前一个时序帧的输出反馈给当前时序帧的输入.第2节中分析了触发器电路第1个时序帧的PTM的计算方法,为了计算第n个时序帧的PTM,采用新PTM方法进行触发器PTM的迭代计算.图5给出了边沿R-S触发器时序展开的一个实例.

对应于第k个时序帧的边沿R-S触发器的特征方程为Qk=(R↑Qk-1)↑S；第k+1个时序帧的特征方程为Qk+1=(R↑Qk)↑S=(R↑(R↑Qk-1)↑S)↑S.根据定理1和定理2,当输入向量为i=(x1x2…xm)时,边沿R-S触发器的输出概率分布向量为：

因此,边沿R-S触发器在第k+1个时序帧的PTM:

=(F2⊗I2⊗F2)*(I2⊗Prs-FF-e,k⊗I2)*Prs-FF-e

因此,就得到了如下计算PTM的迭代方程:

Prs-FF-e,k+1= (F2⊗I2⊗F2)*(I2⊗Prs-FF-e,k⊗I2)

*Prs-FF-e

其中,Prs-FF-e,Prs-FF-e,k和Prs-FF-e,k+1分别是边沿R-S触发器在第1个时序帧、第k个时序帧和第k+1个时序帧的PTM.用这个迭代方程就可以计算边沿R-S触发器在第n个时序帧的PTM.类似地,可以得到其他类型触发器PTM计算的迭代方程.

3.2 触发器可靠度计算

在触发器PTM计算方法的分析基础上,提出基于PTM的触发器可靠度计算方法:F-PTM方法首先从触发器电路的特征方程出发,再用电路PTM的判定定理推理计算触发器的PTM,并用迭代方式计算出电路在第k个时间帧的PTM,最后,根据输入信号的概率分布函数和式(6)计算出电路的可靠度[14].

(4)

其中,R为电路的可可靠度,P为电路的PTM,它的理想概率转移矩阵为I,输入概率分布为V.

以基本R-S锁存器为例加以说明.基本R-S锁存器的PTM为Prs-latch,无故障时其ITM为Irs-latch,R=S=0为限制输入,其他输入可以认为是均匀分布,即输入概率分布向量Vrs-latch=[0,1/6,0,1/6,1/6,1/6,1/6,1/6]T.基本R-S锁存器的可靠度为:Rrs-latch=‖(Vrs-latch* Prs-latch∘ Prs-latch)‖.

4 实验与分析

实验电路分成三类:①D锁存器,正边沿D触发器,和正沿触发双D型触发器74HC74;②正边沿J-K触发器,主从J-K触发器,和边沿触发双J-K触发器74HC112;③基本R-S与非门锁存器,正边沿R-S触发器,主从R-S触发器,和四个基本R-S锁存器74LS279.假设实验电路中各个逻辑门的差错概率p与当前CMOS技术的水平相适应[9].

4.1 实验数据分析

表2为锁存器和触发器可靠度评估实验数据,其中迭代次数为电路可靠度经过迭代计算后,可靠度收敛时的迭代次数.图6显示了三种触发器电路迭代计算时,可靠度的变化情况.

表2 锁存器和触发器可靠度评估实验数据

进一步分析实验数据可得:①电路的可靠度随着p的增加而减小,这是因为差错概率越大,电路出错的概率就越大,电路可靠度就会变小.②多数电路可靠度随着迭代计算次数的增加而减小.这是因为电路的反馈作用会影响电路的可靠度,例如,图7中R-S触发器和J-K触发器的可靠度随着迭代计算次数的增加而减小.

③电路的可靠度经过迭代计算会收敛于某一确定的值.因为触发器电路本身存在固有的屏蔽作用.例如基本R-S与非门锁存器经过135次迭代后收敛.④所有D锁存器和D触发器的可靠度不会随着迭代次数的增加而减小,如表2和图7所示.这是由于D触发器有其固有的逻辑屏蔽作用强,内部的反馈作用不会影响电路的可靠度.从D触发器的特征方程Qn+1=D也可知道,它的当前状态n不会影响下一状态Qn+1的输出.

4.2 不同方法的比较

MonteCarlo仿真的精确度高,验证实验结果准确性通常与MonteCarlo仿真的实验结果进行了比较[9].F-PTM方法、MP方法的实验结果与也MonteCarlo仿真的实验结果进行了比较.实验中采用MonteCarlo方法时每个电路采样的样本数为50000个,采用F-PTM方法和MP方法实验时可靠度收敛时,评估实验结束.p取三个不同值(1e-6、1e-4、1e-2)的实验结果的相对误差如表3所示.

表3 不同可靠度评估方法的实验结果比较

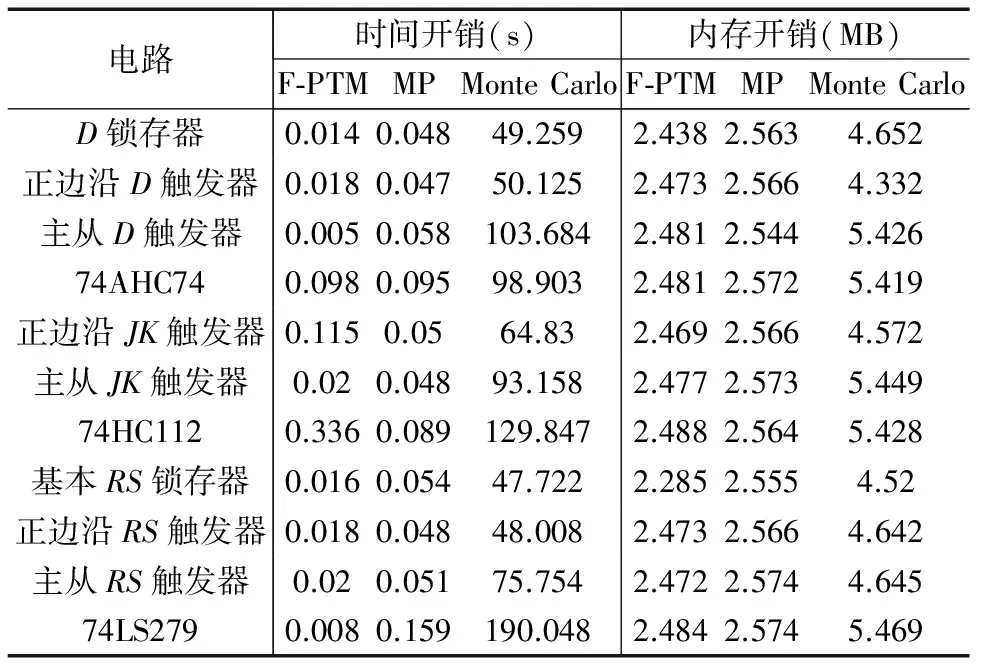
表4 可靠度评估方法的时间开销和内存开销的比较

比较F-PTM方法和MP方法相对Monte Carlo方法的相对误差发现:MP方法实验结果相对误差γMP比F-PTM方法的相对误差γF-PTM更大.因此,实验表明F-PTM方法评估得到的结果更精确.这是因为F-PTM方法是通过计算整个触发器电路的PTM,然后再计算出电路的可靠度,而电路的PTM考虑了所有输入组合的差错概率,并且所有输入组合可以同时计算,不涉及输入向量的采样就可以精确地计算出差错概率.而MP方法用梯度因子方法计算反馈信号对电路可靠度的影响,梯度因子人为设置gr=0.5[9],从而影响评估结果的精度.

表4给出了F-PTM、MP和Monte Carlo等方法实验的时间开销和内存开销.数据表明,F-PTM方法和MP方法的内存开销差别不大,因为触发器可靠度评估实验电路的规模较小.但F-PTM方法的时间开销比Monte Carlo方法小很多.

5 结束语

本文提出了F-PTM方法,用于计算触发器电路可靠度.F-PTM方法从触发器电路的特征方程出发,用电路PTM的判定定理推理计算触发器电路的PTM,并用迭代方式计算电路在第k个时间帧的PTM,最后考虑输入向量的概率分布计算出触发器的可靠度.本文对F-PTM方法的电路PTM判定定理给出了理论证明.与传统的PTM方法相比较,F-PTM方法既能计算组合电路的PTM,也计算触发器电路的PTM,其通用性强.与已有的评估方法相比较,F-PTM方法的实验结果比MP方法的实验结果更为接近Monte Carlo方法的仿真试验结果,表明F-PTM方法评估得到的实验结果更精确.F-PTM方法的后续研究工作在文献[17]中论述.

[1]王真,江建慧.基于概率转移矩阵的串行电路可靠度计算方法[J].电子学报,2009,37(2):241-247.

Wang Z，Jiang J H.A serial method of circuit reliability calculation based on probabilistic transfer matrix[J].Acta Electronica Sinica,2009,37(2):241-247.(in Chinese)

[2]E Taylor,J Han，J Fortes.Towards accurate and efficient reliability modeling of nanoelectronic circuits[A].Proceedings ofSixth IEEE Conference on Nanotechnology[C].Ohio,USA:IEEE Computer Society,2006.395-398.

[3]J Han,E Taylor,J Gao,et al.Reliability modeling of nanoelectronic circuits[A].Proceedings of 5th IEEE Conference on Nanotechnology,2005[C].Nagoya,Japan:IEEE Computer Society,2005.104-107.

[4]G Norman,D Parker,M Kwiatkowska,et al.Evaluating the reliability of NAND multiplexing with PRISM[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2005,24(10):1629-1637.

[5]肖杰,江建慧,等.一个面向缺陷分析的电路成品率与可靠性的关系模型[J].电子学报,2014,(04):747-755.

XIAO Jie;JIANG Jian-hui,et al.A defect analysis-oriented relation model of circuit yield and reliability[J].Acta Electronica Sinica,2005,24(10):1629-1637.(in Chinese)

[6]N Miskov-Zivanov,D Marculescu.Soft error rate analysis for sequential circuits[A].Proceedings of Design,Automation & Test in Europe Conference & Exhibition[C].Nice,France:IEEE Computer Society,2007.1-6.

[7]N Miskov-Zivanov,D Marculescu.Modeling and optimization for soft-error reliability of sequential circuits[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems,2008,27(5):803-816.

[8]H Asadi,et al.Soft error modeling and protection for sequential elements[A].Proceedings of the 20th IEEE International Symposium on Defect and Fault Tolerance in VLSI Systems[C].Monterey,USA:IEEE Computer Society,2005.463-471.

[9]S J S Mahdavi,K Mohammadi.SCRAP:Sequential circuits reliability analysis program[J].Microelectronics Reliability,2009,49(7):924-933.

[10]M R Choudhury,K Mohanram.Accurate and scalable reliability analysis of logic circuits[A].Proceedings of IEEE/ACM Conference on Design,Automation & Test in Europe Conference & Exhibition,2007[C].Nice Acropolis,France：IEEE Computer Society，2007.1-6.

[11]M R Choudhury，K Mohanram.Reliability analysis of logic circuits[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2009,28(3):392-405.

[12]K Lingasubramanian，S Bhanja.Probabilistic error modeling for sequential logic[A].Proceedings of the 7th IEEE Conference on Nanotechnology[C].Hong Kong:IEEE Computer Society,2007.616-620.

[13]K Lingasubramanian,S Bhanja.An error model to study the behavior of transient errors in sequential circuits[A].Proceedings of the 22nd International Conference on VLSI Design[C].New Delhi,India:IEEE Computer Society,2009.485-490.

[14]S Krishnaswamy,G F Viamontes,I L Markov,et al.Accurate reliability evaluation and enhancement via probabilistic transfer matrices[A].Proceedings of the IEEE/ACM Conference on Design,Automation and Test in Europe[C].Orlando,USA:IEEE Computer Society,2005.282-287.

[15]C Ouyang,j Jiang,j Xiao.Reliability evaluation of flip-flops based on probabilistic transfer matrices[A].Proceedings of the 16th IEEE Pacific Rim International Symposium on Dependable Computing(PRDC)[C].Tokyo:IEEE Computer Society,2010.239-240.

[16]D Cheng.Semi-tensor product of matrices and its application to Morgen’s problem[J].Science in China Series F:Information Sciences,2001,44(3):195-212.

[17]欧阳城添,江建慧.基于概率转移矩阵的时序电路可靠度计算方法[J].电子学报,2013,41(1):171-177.

Ouyang C,Jiang J.Reliability estimation of sequential circuit based on probabilistic transfer matrices[J].Acta Electronica Sinica,2013,41(1):171-177.(in Chinese)

欧阳城添(通讯作者) 男,1975年生,江西安远人,博士,主要研究领域为计算机系统结构、容错计算、高层电路可靠性评估.

E-mail:2010oyct@tongji.edu.cn

江建慧 男,1964年生,浙江淳安人,博士,教授,博士生导师,主要研究领域为可信系统与网络、软件可靠性工程、VLSI/SoC测试与容错.

E-mail:jhjiang@tongji.edu.cn

王 曦 女，1974年生，湖南双峰人,博士，主要研究领域为形式化方法、模型检测、高可信系统的安全性分析与评估.

The F-PTM method of Reliability Estimation for Flip-Flops

OUYANG Cheng-tian1,2,JIANG Jian-hui1,WANG Xi2

(1.SchoolofSoftwareEngineering,TongjiUniversity,Shanghai201804,China;2.FacultyofInformationEngineering,JiangxiUniversityofScienceandTechnology,Ganzhou,Jiangxi341000,China)

The traditional method based on probabilistic transfer matrices (PTM) enables accurate evaluation of reliability for moderately large combinational circuits,but it can only be applied to combinational circuits.Flip-flop is an important component of sequential circuits,and its reliability estimation is essential for reliability analysis of sequential circuits.Therefore,a general computational framework for reliability estimation of flip-flops based on PTM (F-PTM) and a decision theorem of circuit’s PTM are proposed.Firstly,a logical function of the flip-flop circuit is expressed;and then its PTM is calculated by deduction employing the proposed decision theorem;finally,the circuit’s reliability is estimated by probability distribution of its inputs.Compared with the traditional PTM method,the F-PTM method can calculate PTMs for both combinational circuits and flip-flop circuits.Experimental results of the classical flip-flop circuits and 74X series circuits show that the F-PTM method is efficient and feasible.The comparison of our method with multiple-pass method and Monte Carlo simulation also demonstrate that the reliability results estimated by the F-PTM method is more accurate.

soft error;flip-flop;reliability estimation;probabilistic transfer matrix;semi-tensor product

2014-08-14;

2015-10-10;责任编辑：梅志强

国家自然科学基金(No.61561024，No.61432017，No.61462034);江西省教育厅项目(No.GJJ14429);江西省自然科学项目(No.20151BAB207035)

TP302.8

A

0372-2112 (2016)09-2219-08

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.09.029