CSAMT全区视电阻率的定义
2016-11-25龚育龄郑燕青
彭 亚,龚育龄,余 安,郑燕青
(东华理工大学 放射性地质与勘探技术国防重点学科实验室,江西 抚州 344000)
CSAMT全区视电阻率的定义
彭 亚,龚育龄,余 安,郑燕青
(东华理工大学 放射性地质与勘探技术国防重点学科实验室,江西 抚州 344000)
为了能够更好地利用过渡区的数据,寻求一种新的全区电阻率定义方法,在CSAMT的基本理论上,通过迭代求解方式计算求解得到全区视电阻率定义公式。使用CSAMT1D程序进行了不同层状模型水平电偶源激发的电磁场的计算,模型成图,分析,以此为基础计算Ex和Ex/Hy全区视电阻率。分析和比较6种模型改变不同参数得出的卡尼亚视电阻率和全区视电阻率对比,分析了不同参数下迭代效果,得出全区视电阻率能够充分利用过渡带数据和近场数据,具有更好的分层特性和实际应用价值。
可控源音频大地电磁法;全区视电阻率; 卡尼亚电阻率; 视电阻率
1 引 言
CSAMT根据波数与收发距的乘积的不同,将测量区域分为远区、近区和中间区,卡尼亚视电阻率是采用由均匀大地导出的远区的视电阻率。利用大地电磁测深的理论,在远区卡尼亚视电阻率能够客观地反映地电断面的垂向变化。但是在中间区和近区的视电阻率会发生严重的畸变,并不能准确地反映地电断面[7]。在地球物理的野外勘探中,大多数人都是在波区进行测量,但是在现实中往往受工作条件和发射功率等的限制,特别是在高阻的测量地区,常常不得不在中间区甚至近区进行测量。但是在近区的话,电磁场是不具有频率测深的条件,所以只能进行几何测深;在中间区的话,往往也会抛弃这些数据,但是电磁场在中间区域仍然有大量的可利用信息,而很多野外数据也正是在中间区观测的,如果放弃这些数据不用,将会造成一些必要的不准确的解释。针对这种情况,许多学者提出不少的中间区校正的方法,但是都存在某些不足。汤井田、何继善采用迭代的方法求得全区视电阻率,全区视电阻率在所有区域都能正确反映地电断面垂向变化[5]。CSAMT的反演解释一般是先把近区和中间区视电阻率校正到相当于远区的视电阻率,然后采用MT的反演理论进行反演[1]。但是由于目前近区和中间区校正存在的问题,由近区和中间区校正得到的数据精度不高,导致反演的结果不够理想。针对以上情况,很多学者想采用全区视电阻率进行反演,这是因为全区视电阻率是由多次迭代得到的。本文正是介绍用多次迭代得到全区视电阻率,使得地质资料解释更加准确和全面。
2 CSAMT全区域视电阻率的定义
2.1 电场Ex全区视电阻率的定义由均匀半空间模型CSAMT电磁场Ex分量的计算公式可知,可提取电阻率表达式[1,2]为:
(1)
该公式ρ为电阻率,Ω·m;Ex为电场,单位V/m;k为波数,r为半径单位m;PE=I·dl;I为电流,单位Ω;l为收发距,单位m;φ为角频率。左边为大地电阻率,右边波数k也含有大地电阻率。因此该公式的定义为隐式表达,需要通过迭代求解方法求取。
2.2 电场Ex和磁场Hy的全区视电阻率的定义在CSAMT测量过程中,当满足波区条件时,视电阻率可采用卡尼亚来定义的方式来求取[4],即:
(2)
其中角频率ω=2πf,μ=4π10-7,在标准模型中,PE=I·dl=1,根据水平方向的电场Ex和与之垂直方向的磁场Hy的值,就可求出水平层状的卡尼亚电阻率。
(3)

(4)
其中I0,I1,K0,K1为以kr/2为变量的贝塞尔函数。
2.3 CSAMT全区视电阻率正演迭代拟合
迭代思想:根据解非线性方程求解定义全区视电阻率。
在测试条件一定的条件下,各电磁场分量为地下介质电阻率、介电常数及磁导率的复杂函数。可采用非线性方程求解方法求解出电阻率、介电常数及磁导率。同直流电阻率法,这样定义的参数可称为视参数,即视电阻率、视磁导率、视介电常数。
迭代步骤:
①给出全区视电阻率初值ρ(0)。此初值是任意的,可选取为相应的波区视电阻率;
②将ρ(0)代入公式,进而求得第一次迭代视电阻率值ρ(1);

第一种迭代公式:
由公式(1)可知:推出迭代公式
(5)

第二种迭代公式:
由公式(4)可知:推出迭代公式
(6)
其中I0,I1,K0,K1为以kr/2变量的虚棕量贝塞尔函数。给定视电阻率初值ρ(0),将k中的电阻率设定为ρ(0),将ρ(0)代入公式(6),进而求得第一次迭代视电阻率值ρ(1);再根据迭代步骤得出视电阻率。
3 CSAMT全区视电阻率的响应特征
3.1 均匀半空间
参数的选择
在层状介质中,在设定标准模型中,任意取16种不同的频率下的标准模型,这频率f选择(0.01,0.1,0.2,0.5,0.8,1,2,5,8,10,20,50,80,100,200,500),收发距r=2 000 m。
设定模型电阻率为ρ1=100 Ω·m,可以对均匀半空间表面水平偶极源产生的电磁场进行视电阻率计算以及迭代,得出视电阻率,见图1。
由图1可以看出在均匀半空间中,全区视电阻率在远区和过渡区就等于卡尼亚电阻率,由电场强度拟合后的全区视电阻率在近区经过改正以后,比较直观地反映了地下电性的垂向变化特征,与已知地质资料比较相符合。
3.2 二层介质
3.2.1 D型模型
设定模型电阻率为ρ1=100Ω·m,ρ2=1 Ω·m,可以对均匀半空间表面水平偶极源产生的电磁场进行视电阻率计算以及迭代得出的视电阻率,见图2。
由图2可以看出,卡尼亚电阻率和全区视电阻率曲线形态大致相同。全区视电阻率在远区和过渡区就等于卡尼亚电阻率,在过渡区和远区时,曲线大致呈45°上升。由电场强度拟合后的全区视电阻率在近区经过改正以后,符合设定的模型。
3.2.2 G型模型
设定模型电阻率为ρ1=1 Ω·m,ρ2=100 Ω·m,可以对均匀半空间表面水平偶极源产生的电磁场进行视电阻率计算以及迭代得出的视电阻率,见图3所示。

图1 均匀半空间电阻率曲线 Fig.1 Resistivity curve in homogeneous half space
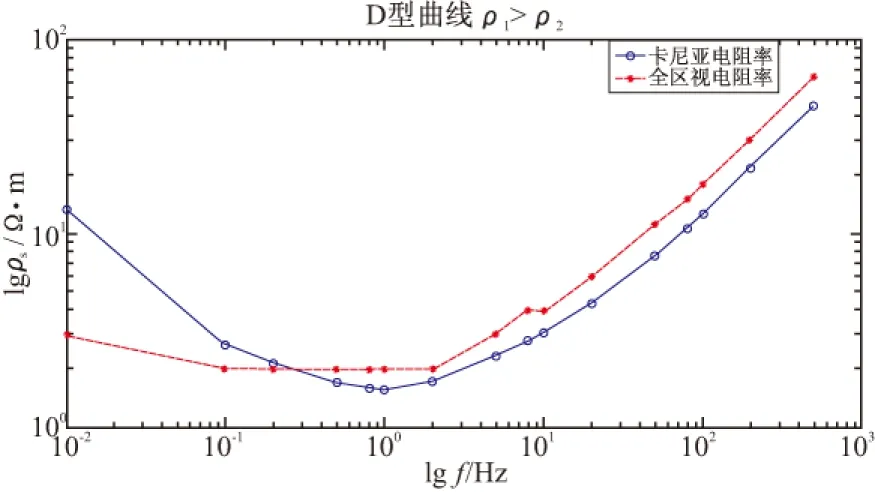
图2 D型电阻率曲线 Fig.2 D-type resistivity curves
由图3可以看出,在二层介质模型中,卡尼亚电阻率和全区视电阻率曲线形态大致相同。在低于1 Hz时卡尼亚电阻率发生严重的畸变,全区视电阻率在低频时偏差也较小,说明全区视电阻率定义视电阻率效果较好。
3.3 三层介质
3.3.1 A型模型
设定模型电阻率为ρ1=1 Ω·m,ρ2=10 Ω·m,ρ3=100 Ω·m,可以对均匀半空间表面水平偶极源产生的电磁场进行视电阻率计算以及迭代得出的视电阻率,如图4所示。
由图4可以看出,在三层介质模型中,在低于1 Hz时卡尼亚电阻率发生严重的畸变,在中间区,曲线形态大致相同,在远区,曲线形态大致相似。全区视电阻率在低频时偏差也较小,说明全区视电阻率定义视电阻率效果较好。
3.3.2 Q型模型
设定模型电阻率为ρ1=100 Ω·m,ρ2=10 Ω·m,ρ3=1 Ω·m,可以对均匀半空间表面水平偶极源产生的电磁场进行视电阻率计算以及迭代得出的视电阻率,见图5。
由图5可以看出,在三层介质模型中,在低于1 Hz时卡尼亚电阻率发生严重的畸变,在中间区,曲线形态大致相同,在远区,曲线形态大致相似。全区视电阻率在低频时偏差也较小,说明全区视电阻率定义视电阻率效果较好。
3.3.3 H型模型
设定模型电阻率为ρ1=10 Ω·m,ρ2=1 Ω·m,ρ3=100 Ω·m,可以对均匀半空间表面水平偶极源产生的电磁场进行视电阻率计算以及迭代得出的视电阻率,见图6所示。
由图6可以看出,在三层介质模型中,在低于0.1 Hz时卡尼亚电阻率发生严重的畸变,在中间区,曲线形态大致相同,在远区,曲线形态大致相似。全区视电阻率在低频时偏差也较小,在远区时,曲线大致呈45°上升。说明全区视电阻率定义视电阻率相对于卡尼亚电阻率效果较好。
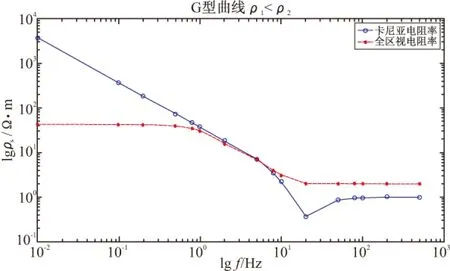
图3 G型电阻率曲线 Fig.3 G-type resistivity curves

图4 A型电阻率曲线 Fig.4 A-type resistivity curves
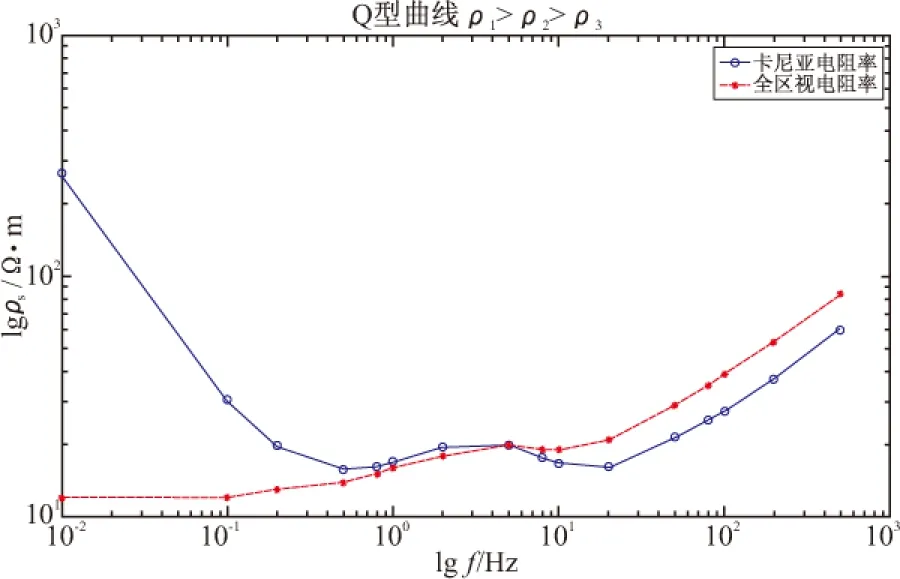
图5 Q型电阻率曲线 Fig.5 Q-type resistivity curves

图6 H型电阻率曲线 Fig.6 H-type resistivity curves
3.3.4 K型模型
设定模型电阻率为ρ1=10 Ω·m,ρ2=100 Ω·m,ρ3=1 Ω·m,可以对均匀半空间表面水平偶极源产生的电磁场进行视电阻率计算以及迭代得出的视电阻率,见图7。
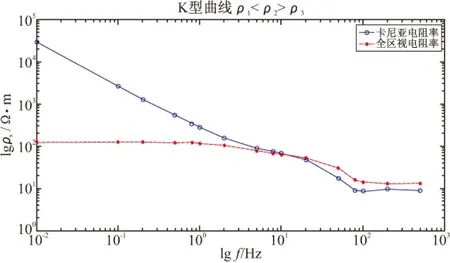
图7 K型电阻率曲线Fig.7 K-type resistivity curves
由图7可以看出,在三层介质模型中,在低于1 Hz时卡尼亚电阻率发生严重的畸变,在中间区,曲线形态大致相同,在远区,曲线形态大致相似。全区视电阻率在低频时偏差也较小,说明全区视电阻率定义视电阻率效果较好。而且相对来说,卡尼亚电阻率在近区的数据起伏较大,不准确,但是全区视电阻率很好地克服了这一困难。
4 结 论
1)用电场强度拟合电阻率在远区就等于卡尼亚电阻率,在近区经过改正以后,能够比较直观地反映地下电性的垂向变化特征。
2)通过CSAMT电场分量与之垂直的磁场分量的之比得到的阻抗来定义全区域视电阻率,具有局限性、唯一性。
3)拟合差越小,反演效果越好。频点选取越多,迭代效果越好。
4)成果效果图与模型设定的频率有关,尤其是在高频段比较明显。
5)成果效果图与模型的收发距也有一定的关系,所以在设定参数时需考虑参数的合理性和准确性。
[1]朴化荣.电磁测深法原理[M].北京:地质出版社,1990.
[2]何继善.可控源音频大地电磁法[M].长沙:中南大学出版社,1990.
[3]周茂军,周玉冰.可控源音频大地电磁法(CSAMT)的近场效应和近场校正[J].辽宁地质,1993,9(3):271-281.
[4]殷哲琦,张志勇,黄临平,等.基于二次场算法的CSEM二维有限单元法正演[J].东华理工大学学报(自然科学版),2015,38(2):194-199.
[5]石昆法.可控源音频大地电磁法理论与应用[M].北京:科学出版社,1999.
[6]詹少全,钱美平,冯戋戋.CSAMT 全区视电阻率电场正演迭代拟合近场校正方法[J].物探与化探,2011,35(5):663-665.
[7]田继枫.可控源音频大地电磁法视电阻率参数计算方法研究[D].北京:中国地质大学,2011.
[8]邝广.可控源音频大地电磁法的场区校正[J].中国煤炭地质,1996,8(3):74-77.
[9]夏媛媛,赵明,藏歌,等.正演模拟技术在解释反演中的应用[J].工程地球物理学报,2014,11(6):842-846.
[10]马为.CSAMT在镜泊湖玄武岩覆盖区深部地热勘查中的应用[J].工程地球物理学报,2015,12(4):450-454.
[11]曾国.大地电磁二维有限元正演数值模拟[D].长沙:中南大学,2008.
The Definition of the All-time Apparent Resistivity CSAMT
Peng Ya,Gong Yuling,Yu An, Zheng Yanqing
(FundamentalScienceonRadioactiveGeologyandExplorationTechnologyLaboratory,EastChinaInstituteofTechnology,FuzhouJiangxi344000,China)
In order to be able to make more and better use of the transition zone data, a new definition of the all-time apparent resistivity method should be sought. Through iteration calculation, the all-time apparent resistivity defining formula can be gotten on the basis of CSAMT basic theory. CSAMT1D procedures can be used to calculate, map and analyze horizontal electric dipole source excitation in different layered model in electromagnetic field, based on which theExandEx/Hyall-time apparent resistivity has been calculated. Different parameters of Cagniard resistivity changed by six models are analyzed and compared with the all-time apparent resistivity, and the next iteration effect of different parameters is also analyzed. The exploration finds that the apparent resistivity region can make full use of the transition zone and near-field data, which have hierarchical nature and practical value.
CSAMT; all-time apparent resistivity; Cagniard resistivity; apparent resistivity
1672—7940(2016)02—0161—05
10.3969/j.issn.1672-7940.2016.02.004
国家自然科学基金(青年)项目(编号: 41104074)
彭 亚(1990-),男,硕士研究生,主要从事电磁法勘探的学习与研究。E-mail:15970439080@163.com
龚育龄(1960-),男,教授,主要从事勘查地球物理专业的教学和科研工作。E-mali:ylgong@ecit.com
P631.3
A
2015-10-18
