煤田积水采空区井地电位法三维有限差分正演模拟

邱卫忠，张 辉，唐新功，严良俊，张雷洁

(1.山西省煤田地质115勘察院，山西 大同 037039;2.长江大学 地球物理与石油资源学院，湖北 武汉 430100)



煤田积水采空区井地电位法三维有限差分正演模拟

邱卫忠1，张 辉2，唐新功2，严良俊2，张雷洁1

(1.山西省煤田地质115勘察院，山西 大同 037039;2.长江大学 地球物理与石油资源学院，湖北 武汉 430100)

煤田积水采空区是威胁矿井安全的主要因素之一。针对井地电位法特定的边值问题，推导出了相应的有限差分格式，结合煤田积水采空区的电性特征及分布特点，设计了多个地电模型，分别利用有限差分法对其进行了正演模拟。正演结果表明，井地电位法对单个积水采空区及横向上分布的多个积水采空区识别能力较好，而对垂向分布的多个积水采空区识别能力较弱。研究结果对于煤田积水采空区的探测研究具有一定的参考价值。

煤田积水采空区；井地电位法；有限差分法；三维正演

1 引 言

矿井的水害事故是煤田生产中重要的灾害之一，是仅次于瓦斯事故的第二大煤矿事故，其中采空区积水在水害事故占有相当大的比重[1]。同时，采空区积水具有突发性强，突水量大，破坏性强等特点，是威胁矿井安全的主要因素之一[2]。因此，做好煤田积水采空区的探测工作，对矿井水害事故的防治具有积极的意义。

作为无损探测的电磁探测方法，由于其对含水体敏感、分辨能力较高，因此在煤田水文地质勘探中获得了广泛的应用。但在地下结构复杂，目的层埋深又较深的情况下，地面物探方法会由于探测深度不够、信号不强、干扰太大等原因，无法采集到高质量的物探数据，给后期的资料处理与解释造成很大的困难，不能得出精确的结果。

为克服常规地面物探方法的缺陷，地—井物探方法开始逐渐兴起，井地电位法便是其中的代表之一。它是近几年发展起来的一种电磁勘探新方法和新技术。井地电位法是通过套管井向地下供入大功率电流，在地表观测由于地下介质的电性变化引起的电位异常，据此来分析地下导电体的电性分布情况。相比于传统的电阻率法，井地电位法具有勘探深度大、探测范围广、分辨率高等特点[3]。

从20世纪70年代开始，一直到本世纪初，井地电位法在圈定煤层、油气边界以及确定深部矿藏等领域不断取得成果[4]。这一阶段对井地电位法的研究，还集中在定性解释和物理模拟[11，12]上，数值模拟研究较少。此后，徐凯军等[13]、刘地渊等[14]、苏朱刘等[15]、王志刚等[16]、屈有恒等[17]、柯敢攀等[18]先后分别使用多种数值方法，对油田井地电位法的三维正反演问题展开了研究。近年来，戴前伟等[19]、李芸芸[3]还开展了复杂地形条件下的井地电位法三维数值模拟研究，取得了一定的效果。

随着井地电位法在煤田积水采空区探测中的进一步应用，结合煤田积水采空区的特点，继续深入开展煤田井地电位法的三维数值模拟是非常必要的。有限差分法作为应用最早、最经典的数值模拟方法，依靠其相对简单的理论基础及简便的计算过程，在地球物理工作中应用非常广泛[20-22]。本文利用有限差分算法，结合井地电位方法在煤田积水采空区中的应用，进行三维正演模拟研究，探讨地井电位法对不同位置积水采空区的探测效果。

2 井地电位法的边值问题

井地电位法的工作原理如图1所示，在地表向被测井A施加一个大功率电流，同时在无穷远处选择另一口井B作回流电极。两个供电电极的金属套管，全部用水泥封固。由于水泥胶结致密，因此电流主要通过地表及地下目的层流向地层，造成地层中的电流密度分布不均匀，但是电流几乎垂直于套管壁流出。同时，由于套管直径与套管长度相比可以忽略，因此在井地电位法的正演模拟、反演成像以及后期的数据处理过程中，一般都将套管当作线电流源来处理。

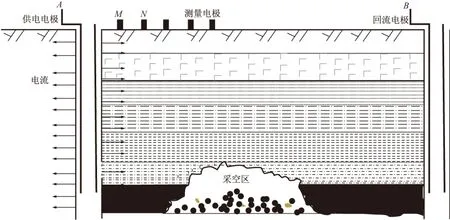
图1 井地电位法工作原理示意图Fig.1 Schematic map of borehole-surface potential method

在非均匀各向同性的三维介质中，点电流源产生的电位U可以用如下的边值问题来描述[3]：

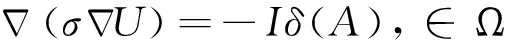
(1-1)

(1-2)

(1-3)

式(1)中，I为供电电流大小，σ为电阻率ρ的倒数，δ(A)为δ函数，Γs和Γ∞分别是研究区域Ω的地表边界和地下边界，n为地下边界的外法线方向，r为点电流源A到边界点的距离，cos(r,n)为n与r之间夹角的余弦值。

线电流源的本质，其实可以看成是无数个点电流源的叠加。而根据叠加原理，几个点电源在空间中某处电位的大小，等于各个点电源单独存在时在该点产生的电位大小的代数和。因此，在井地电位法对线电流源的正演模拟中，可以将线电流源剖分成多个点电流源，分别对点电流源产生的电位U做正演模拟，再将得到的结果进行叠加处理，便得到线电流源的响应。

3 有限差分法的格式推导

对三维求解区域进行网格离散化处理，采用直角坐标系，如图2所示。

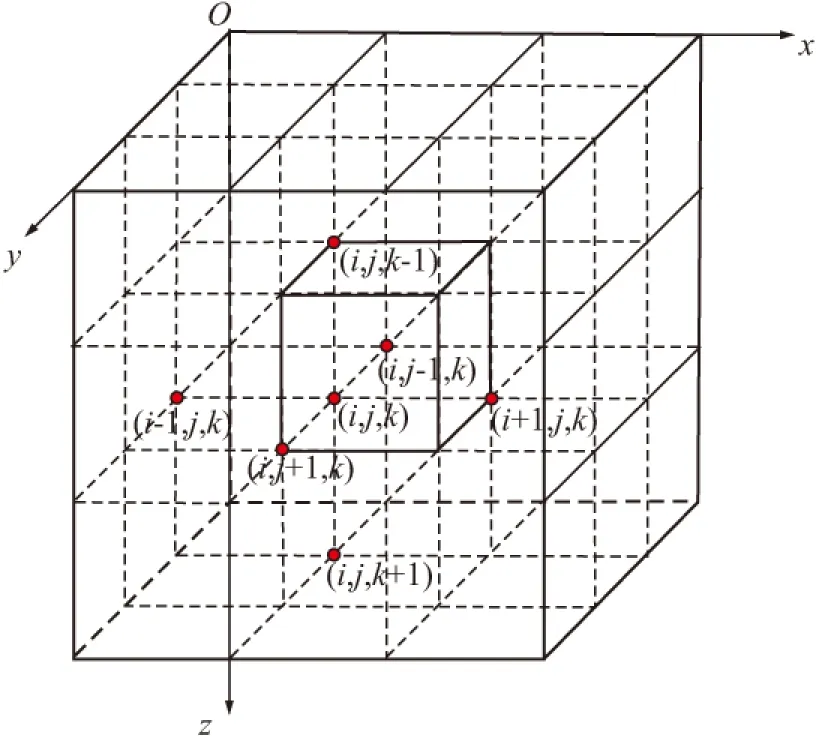
图2 求解区域网格离散示意图Fig.2 Schematic map of mesh grid discretization

利用有限差分法的原理：用差商来代替导数，可以写出任意网格节点(i,j,k)处电位U的一阶差商和二阶差商分别为：

(2-1)

(2-2)

(2-3)

(3-1)

(3-2)

(3-3)

因此，对于线电流源L的任一线元dL，电流大小设为dI，式(1)可以写为：

=-dIδ(i,j,k),∈Ω

(4-1)

(4-2)

(4-3)

利用边界条件，在每一个网格节点处得到一个方程，联立方程组，数值求解即可得到区域内任意节点处的电位U。叠加所有线元dL正演得到的U，便可得到线电流源L在空间各处产生的电位大小。

4 三维模型的正演计算

利用上述的三维有限差分算法，计算均匀半空间条件下线电流源在地表产生的电位，与解析解之间的误差大小如图3所示。此检验模型的网格步长为1 m，网格区域大小为15 m×15 m×30 m，线源L位于地表中心处，长度为10 m。

从图3中可以看出，除源点附近电位值有所畸变外，区域内的其他测点误差大小都在可以接受的范围内。因此可以认为，本文采用的三维有限差分算法是正确的。

由于煤田的积水采空区往往不止一层，所以开展三维空间中多个异常体的异常响应的研究是很有必要的。考虑到积水区范围有限，结合采空区积水的电性特征，设计了如下3个地质模型：①单个低阻异常体，代表单个积水采空区；②垂向的两个低阻异常体，代表不同深度的两个积水采空区；③横向的两个低阻异常体，代表埋深相同、但横向不同位置的2个积水采空区模型。分别研究在井中激发、地表接收时的视电阻率值，以此分析井地电位法对地下不同位置煤田积水采空区的识别能力。

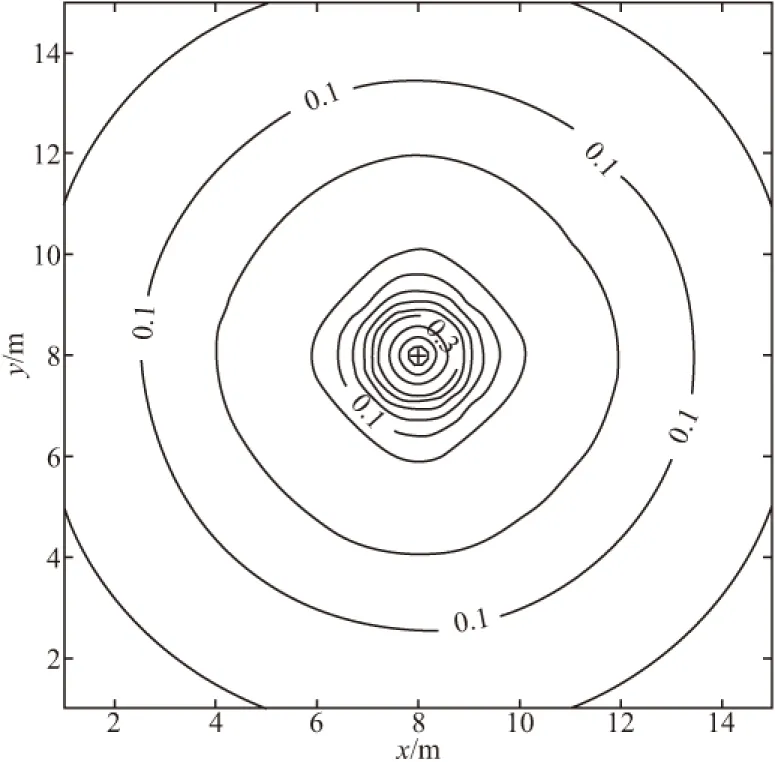
图3 数值解与解析解的误差Fig.3 The rms error of numerical solution and analytical solution

在本文所有的模型中，背景电阻率均取为100 Ω·m，异常体电阻率为1 Ω·m，线源长度L为10 m，有限差分网格步长为1 m。模型①、②的异常体大小为5 m×5 m×1 m，网格区域大小为60 m×15 m×30 m，测距MN=1.414 m，指向为平行于y=x的方向。模型③的异常体大小为5 m×5 m×5 m，网格区域大小为60 m×15 m×30 m，测距MN=1 m，指向为平行于y=0的方向。

4.1 单个低阻异常体

图4为均匀半空间中单个异常体模型的示意图，图中实线小长方体为异常体，垂直实线L代表放置于井中的垂直线源。图5(a)、(b)分别为图4中异常体埋深为3 m、5 m时的视电阻率等值线图，图5中黑色十字与方框分别代表垂直线源和异常体在地面上的投影位置。从图5中可以看到对应于视电阻率明显偏低的区域与低阻异常体位置吻合较好，而随着埋深的增加，异常响应会有所减小。在低阻异常区域的两端，出现了一个不太明显的高阻假象，这可以利用视电阻率的微分形式来解释[23]。同时由于源的奇异性，在源附近视电阻率值不准确。

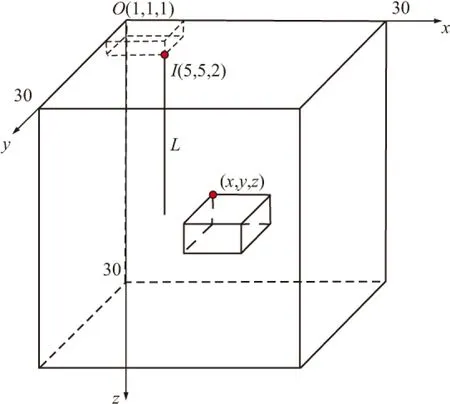
图4 单个异常体模型示意图Fig.4 Schematic map of one anomaly body model

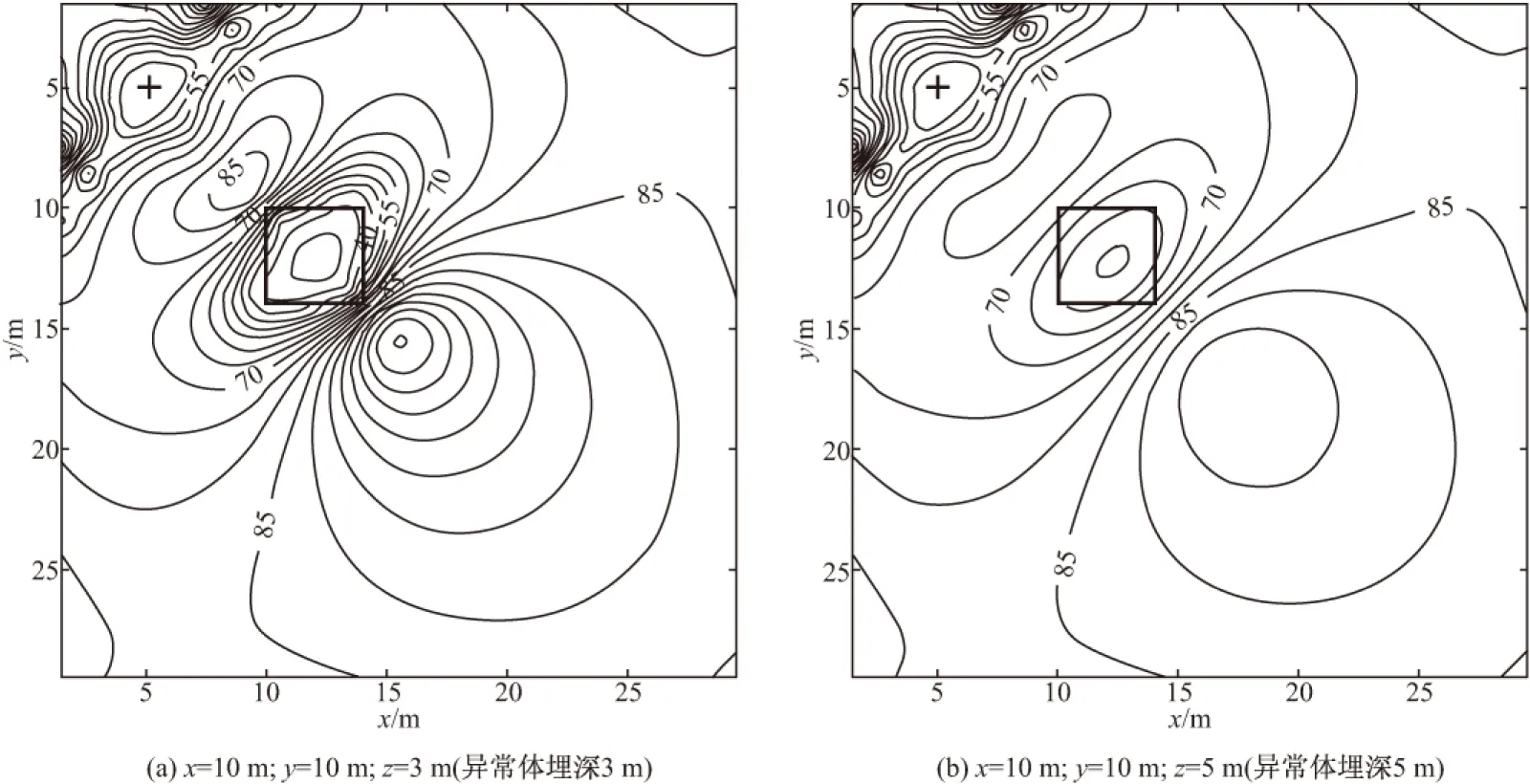
图5 模型①视电阻率的等值线Fig.5 The apparent resistivity contour map of the first model

4.2 垂向的两个低阻异常体

图6为垂向上两个异常体模型的分布示意图，来模拟地下三维空间中不同深度上的多个积水采空区情况。两个异常体的埋深分别为5 m和10 m，水平方向顶点坐标均为(10,10)。相应的视电阻率等值线图如图7所示。从图7可以看到，与图5相同，在低阻体相应位置有一个低阻异常区域，同时与只有一个埋深为5 m的异常体(图5b)相比，低阻异常数值上略微增加，这是由于叠加了10 m的低阻异常体的响应的原因。但仅从地表观测的电位上，很难直接分辨埋深为5 m与10 m的两个异常体。这说明，对于煤田中深度不同的多个积水采空区，井地电位法的分辨能力并不理想。

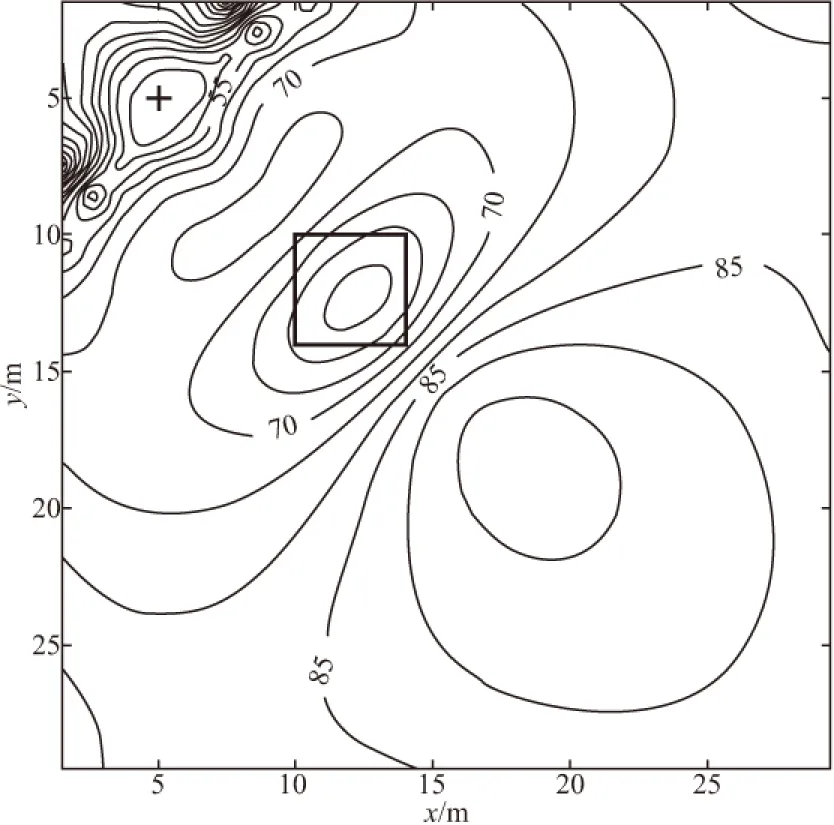
图7 模型②视电阻率等值线Fig.7 The apparent resistivity contour map of the second model

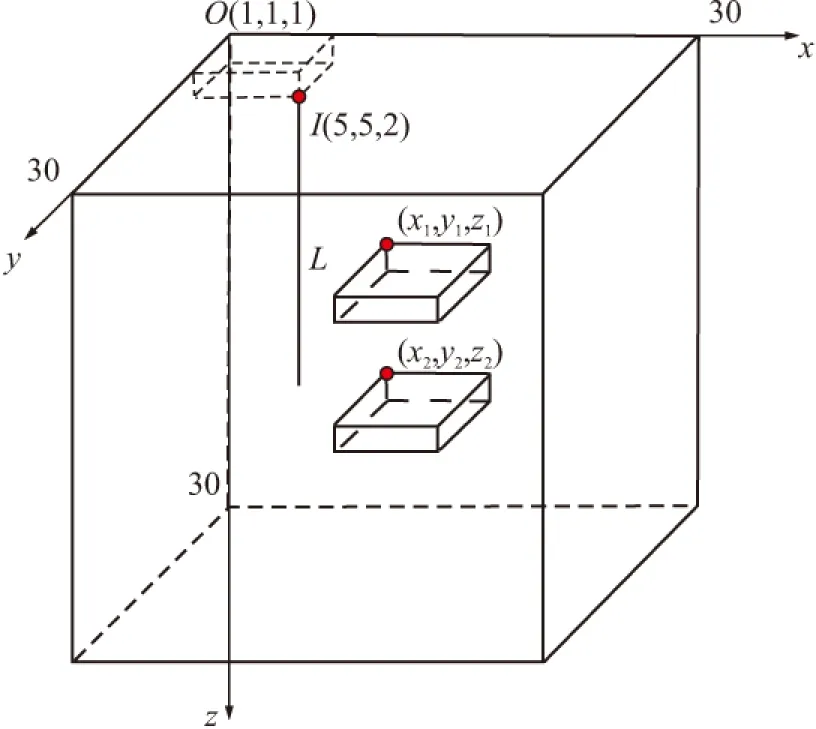
图6 垂向两个异常体模型示意图Fig.6 Schematic model of two anomaly bodies distributed vertically

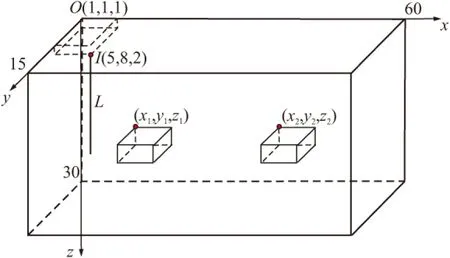
图8 横向两个异常体模型示意图Fig.8 Schematic model of two anomaly bodies distributed transversely

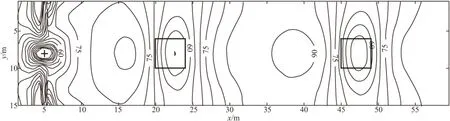
图9 模型③视电阻率等值线Fig.9 The apparent resistivity contour map of the third model

4.3 横向的两个低阻异常体

图8为横向两个异常体模型的示意图，以此来模拟地下空间中水平位置不同的积水采空区。两个异常体的埋深均为5 m，水平方向顶点坐标分别为(20,6)和(45,6)。其相应的视电阻率等值线图如图9所示。从图9可以看到，在两个低阻体的对应位置都有一个明显的低阻异常区域，并且数值大小也非常接近。这一模型的正演结果表明，井地电位法对水平位置不同的多个积水采空区有较好的识别效果。

5 结 论

针对广泛应用于煤田积水采空区探测的井地电位法，本文利用有限差分法做了三维正演模拟研究，研究表明：井地电位法对一定深度范围内的积水采空区有良好的识别能力，但对垂向分布的多个积水采空区的分辨能力较弱，而对水平位置不同的多个积水采空区分辨能力较好。

[1]董书宁,虎维岳.中国煤矿水害基本特征及其主要影响因素[J].煤田地质与勘探,2007,35(5):34-38.

[2]宋东日,谭湘龙,李杰.煤矿矿井水害的分析和防治方法[J].科技和产业,2009,9(4):65-66.

[3]李芸芸.起伏地形井地电位三维有限元数值模拟[D].长沙:中南大学,2014.

[4]Daniels J. Three-dimensional resistivity and induced-polarization modeling using buried electrodes[J]. Geophysics, 1977, 42(5):1 006-1 019.

[5]Sill W R, Ward S H. Electrical Energizing of Well Casings[M]. Utah: University of Utah, Department of Geology and Geophysics, 1978.

[6]Rocroi J P, Koulikov A V. The use of vertical line sources in electrical prospecting for hydrocarbon[J]. Geophysical Prospecting, 1985, 33(1): 138-152.

[7]张金成.电位法井间监测技术[J].地震地质,2001,23(2):292-300.

[8]凌明友,郝新武,程同军，等.井—地电位成像技术研究剩余油分布[J].断块油气田,2003,10(4):55-58.

[9]谭河清,沈金松,周超，等.井—地电位成像技术及其在孤东八区剩余油分布研究中的应用[J].石油大学学报(自然科学版),2004,28(2):31-37.

[10]何展翔,刘雪军,裘尉庭，等.大功率井—地电法油藏边界预测技术及效果[J].石油勘探与开发,2004,31(5):74-76.

[11]王志刚,何展翔,魏文博，等.井地电法三维物理模型试验[J].石油地球物理勘探,2005,40(5):594-597.

[12]刘昱,王志刚,何展翔.井地电法供电电场分布模拟研究[J].工程地球物理学报,2006,3(5):331-336.

[13]徐凯军,李桐林.垂直有限线源三维地电场有限差分正演研究[J].吉林大学学报(地球科学版),2006,36(1):137-141.

[14]刘地渊,徐凯军,赵广茂，等.任意形状线电流源三维地电场研究[J].地球物理学进展,2006,21(2):395-399.

[15]苏朱刘,杨志冬,李宏，等.电位法在油储动态监测中的应用[J].石油天然气学报(江汉石油学院学报),2006,28(2):56-59.

[16]王志刚,何展翔,魏文博，等.井地电法的准解析近似三维反演研究[J].石油地球物理勘探,2007,42(2):220-225.

[17]屈有恒,张贵宾,晋风明.倾斜线源的三维电场数值模拟研究[J].物探化探计算技术,2007,29(5):431-435.

[18]柯敢攀,黄清华.井地电法的三维正反演研究[J].北京大学学报(自然科学版),2009,45(2):264-272.

[19]戴前伟,陈德鹏,刘海飞，等.复杂管网线源井地电位三维有限元模拟[J].石油地球物理勘探,2012,47(6):998-1 005.

[20]李双喜,曾昭发,李静，等.探地雷达极化探测时域有限差分法模拟效果分析[J].工程地球物理学报,2014,11(4):513-521.

[21]郑冰,李柳德.高密度电法不同装置的探测效果对比[J].工程地球物理学报,2015,12(1):33-39.

[22]徐正玉,杨海燕,邓居智，等.回线源三维地—井瞬变电磁法FDTD数值模拟[J].工程地球物理学报,2015,12(3):327-332.

[23]李金铭.地电场与电法勘探[M].北京:地质出版社,2005.

Three-dimensional Finite Difference Forward Modeling of Borehole-Surface Potential Method in Water Accumulating Gob in Coalfield

Qiu Weizhong1，Zhang Hui2,Tang Xingong2,Yan Liangjun2,Zhang Leijie1

(1.115CoalfieldGeologicalSurveyInstituteofShanxiProvince,DatongShanxi037039,China;2.SchoolofGeophysicsandOilResources,YangtzeUniversity,WuhanHubei430100,China)

Water accumulating gob in coalfield is one of the factors threatening mining safety. According to the special boundary value problem of borehole-surface potential method, the corresponding finite difference scheme is derived in this paper. Combining with the electrical characteristics and the distribution features of water-accumulating gob, a series of geo-electric models are designed to calculate their electric responses by using 3D finite difference approach. The forward modeling results show that the detection ability of borehole-surface potential method for a single water accumulating gob and multiple gobs which distributed transversely is good, while the detection ability for multiple gobs distributed vertically is relatively weak. The result has reference value for the detection of water accumulating gobs in coalfield.

Water accumulating gob; Borehole-surface potential method; Finite difference method; Three-dimensional forward modeling

1672—7940(2016)02—0149—06

10.3969/j.issn.1672-7940.2016.02.002

国家自然科学基金项目(编号：41274115，41274082，41404087，41504096)；973计划项目(编号：2013CB228605)

邱卫忠(1963-)，男，硕士，高级工程师，主要从事电磁法勘探与研究。E-mail：115qwz@sina.com

唐新功(1968-)，男，博士，教授，博士生导师，主要从事电磁法勘探，重磁勘探和岩石物理学的教学与研究。

E-mail：tangxingong@163.com

P631.3

A

2015-11-10