随机需求环境下零售商联合采购与合并运输联盟的稳定性分析

肖 旦，刘 芳，史欣向，秦陇一

（广州大学 工商管理学院，广东 广州 510006）

随机需求环境下零售商联合采购与合并运输联盟的稳定性分析

肖 旦，刘 芳，史欣向，秦陇一

（广州大学 工商管理学院，广东 广州 510006）

在随机需求环境下，企业为了降低运作成本，会进行联合采购与合并运输的战略合作，但是，为了维持所形成合作联盟的稳定性，必须公平合理地分摊联盟的总运作成本.文章采用合作博弈论中的核概念，对随机需求环境下零售商联合采购与合并运输联盟的稳定性展开了分析.①http：//news.cnnb.com.cn/system/2012/09/21/007467919.shtml在需求随机到达的情形下，得到了零售商联合采购与合并运输联盟的最优订货策略；②http：//news.dichan.sina.com.cn/2015/11/01/1132694.html指出零售商进行联合采购与合并运输的战略并不一定总能降低联盟的总期望运作成本，由此提出了零售商合作能降低总期望运作成本的条件；③在可降低总期望运作成本的条件下，提出了按边际成本进行分摊的规则可使大联盟保持稳定，并通过一个具体的实例对成本分摊方案进行了说明.

随机需求；合并运输；订货量；稳定性

采购是企业运作中非常重要的一个环节，据中国物流与采购联合会公布的2012年采购调查数据显示，企业的采购成本占总销售收入的55%①http：//news.cnnb.com.cn/system/2012/09/21/007467919.shtml.因此，如何降低企业的采购成本，一直是学术界和企业经理人所关心的热点问题.近年来，不少企业为了降低产品的采购价格，节省采购的运作费用，结成联合采购合作战略联盟，例如，2015年7月，位于深圳宝能科技园的远见总裁联盟成员中的6家企业共同签订300万元的原材料联合采购协议.此外，还有一些第三方公司也搭建了联合采购的平台，汇集各方的需求，进行统一联合采购，例如，2015年11月，中国房地产采购平台“优采”的建立，实现了恒大地产、华远地产等多家房地产企业针对“铝合金电缆”的联合采购②http：//news.dichan.sina.com.cn/2015/11/01/1132694.html.

虽然联合采购受到了企业经理人的重视，但是，对此开展的研究还主要集中于采用实证与定性的方法，分析联合采购活动将如何降低运作成本或增强企业的谈判能力［1-4］，仅有较少的一些学者对此展开了理论上的分析.例如，MECA等在经典的EOQ和EPQ框架下对此问题进行了一系列的分析，他们在EOQ的框架下，考虑n个零售商协调订货周期，进行联合采购的合作，分别建立了库存成本博弈和持有成本博弈，并在此基础上考虑了价格折扣对于联合采购联盟的影响［5-7］.此外，肖旦等则建立了制造商与零售商的库存合作联盟［8］；肖旦等在产品中含有次品情形下，探讨了多个零售商从同一供应商处订货且进行统一检测的联合采购模型［9］.冯海荣等在不同联合采购情形下讨论了易腐品联合采购费用的分摊问题［10-11］.

然而，在以上研究中，并没有讨论零售商产品合并运输的情况.在实际运作中，为了节省费用，联合采购的产品往往都是由供应商或者第三方物流公司统一配送的.例如，2011年，广州地区的23所高校后勤部门以及餐饮中心负责人一起到广州江南果菜批发市场，进行原材料的集中采购，并将采购到的产品统一配送至各高校①http：//news.cnwest.com/content/2011-03/17/content_4288350.htm.关于多个零售商进行联合采购与合并运输的合作模式，吸引了一些研究人员的关注.目前，FIESTRAS-JANEIRO等在经典的EOQ框架下，讨论了多个零售商联合运输时的成本分摊问题［12］，曾银莲等分别讨论了基于时间的合并运输策略和基于数量的合并运输策略下承运人运输合作的费用分配问题，建立了相应的合作博弈模型，设计了属于核的费用分配方案［13］.但是，他们并未考虑随机需求环境下对零售商联合采购与合并运输联盟订货决策和稳定性的影响.

本文在上述研究的基础上，考虑随机环境下零售商联合采购与合并运输联盟的订货策略、成本分摊规则及其稳定性.得到了随机环境下，零售商联合采购与合并运输联盟的最优订货策略；随后指出随机环境下零售商联合采购与合并运输的合作战略，并不一定能降低总的期望成本，由此给出了合作可以降低总期望成本的条件（即满足次可加性的条件）；并在合作博弈满足次可加性的条件下，根据边际成本给出了可行的成本分摊规则，并证明了在此分摊规则下，可以保持大联盟的稳定.

1 随机环境下零售商联合采购与合并运输联盟的订货量决策

本文在随机需求环境下，考虑n个零售商进行联合采购与基于时间策略的合并运输战略②时间策略的合并运输是指基于时间进行订单合并，即预设一个时间周期，每隔一个周期进行一次合并运输.，其具体背景如下：①每一个零售商面临的订单是随机到达的，令表示零售商i的第J笔订单到达的时间，表示零售商i的第J笔订单和第J+1笔订单到达的间隔时间，即，可假设之间是相互独立并且服从参数为λi的指数分布，因此，在（0，t）时间段内到达零售商i的订单数量Ni（t）服从参数为λit的泊松分布，即E［ Ni（t）］＝λit.②假设零售商i的第J笔订单的需求量相互独立并且服从参数为μ的泊松分布，即E，则零售商i在（0，t）时间段内总的需求量为内，零售商们进行一次各种信息完全共享的联合采购与合并运输，供应商的补货能力无限大，可随时补货并且及时到货，其中，a表示每个零售商每次进行采购的启动费用；c表示零售商采购单位产品的采购成本；Cdi表示从供应商到零售商i（i＝1，2，…n）的运输成本，与供应商到零售商之间的距离成正比，设零售商均位于一条直线上，如果多个零售商形成联合采购与运输联盟S，则联盟S的运输成本为联盟中与供应商距离最远零售商的运输成本，即CdS＝max｛Cdi|i∈S｝.此外，hi表示零售商i（i＝1，2，…n）单位时间内单位产品的持有成本.由于泊松分布之和仍然是泊松分布，因此，对于任意的零售商集合SN，当他们进行联合采购与合并运输时，其总订单到达率满足参数为的泊松分布.

根据随机过程中的更新理论可得出随机环境下，零售商联合采购与合并运输联盟单位时间内的总期望成本为

从而，随机需求环境下，零售商联合采购与合并运输联盟单位时间的最小总期望成本为

2 随机环境下零售商联合采购与合并运输联盟的次可加性

随机环境下，零售商之间会形成不同的联合采购与合并运输联盟，它们将产生不同的运作成本，联盟的成本可以用特征函数c（S）刻画，定义为：一个给定的随机环境下零售商联合采购与合并运输的合作博弈模型为（N，c），其中N表示零售商的集合，c为合作联盟的成本.

下面的定理1将说明在一般情形下，合作博弈（N，c）并不满足次可加性，这与曾银莲等［13］在随机需求环境下零担货物运输合作研究中所得到的结论是不同的.这是因为，在文献［13］中曾银莲等讨论的基于时间策略下的合作运输博弈问题，仅仅考虑了多个零售商将订单通过统一订货周期合并在一起采购产品的情形，并没有考虑产品运输到零售商处的运输成本对于联盟的影响.然而，在实际中不少零售商不仅进行联合采购，而且还进行合并运输，此外，产品送至每个零售商处的运输成本存在差别.因此，本文考虑到运输成本对于零售商结盟的影响，例如，当2个零售商合作时，如果一个零售商的运输成本较高，而另一个零售商的运输成本较低，他们形成联合采购与合并运输联盟所采用的最优订货周期，将可能会使某一个零售商在一个订货周期内的订货量较多，从而使系统产生比分开时还高的成本，即不满足次可加性.

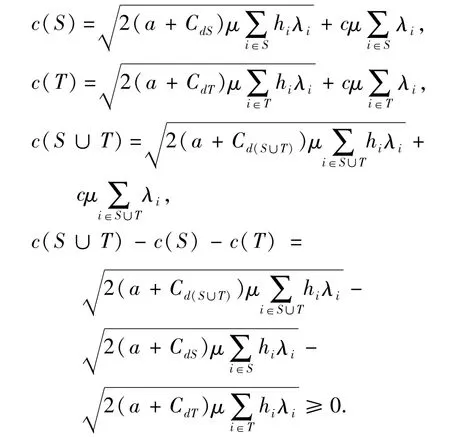
即c（S∪T）≤c（S）+c（T）等价于

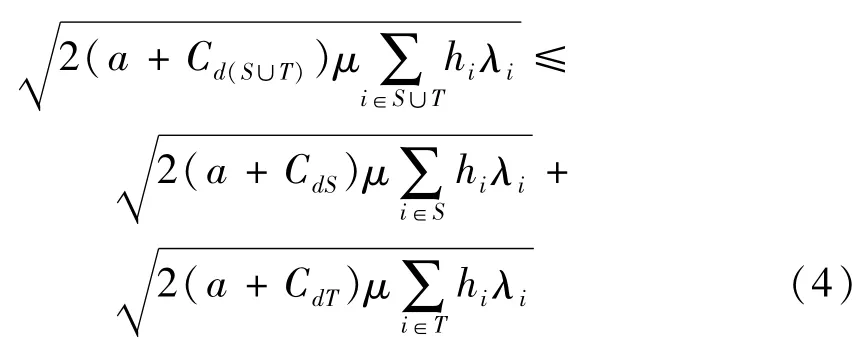
将式（4）两边同时平方后考虑如下2个式子，

3 随机环境下零售商联合采购与合并运输联盟的稳定性

定义2 满足如下条件的集合称为合作博弈（N，c）的核：

定义5 令π（N）是N的所有置换σ：N→N的集合，集合Pσ（i）：＝｛r∈N|σ-1（r）＜σ-1（i）｝含有关于置换σ的所有i的前继.

关于置换σ和合作博弈（N，v）的边际贡献向量mσ（N，v）∈Rn，定义为对所有i∈N，mσ（N，v）的第i个分量为

随机环境下，如果零售商联合采购与合并运输合作博弈（N，c）满足次可加性，则将零售商按照其与供应商之间的距离由远及近降序排列的全体记为π（N，A），从而，联合采购与合并运输大联盟N的运作成本可按如下的规则进行分摊：

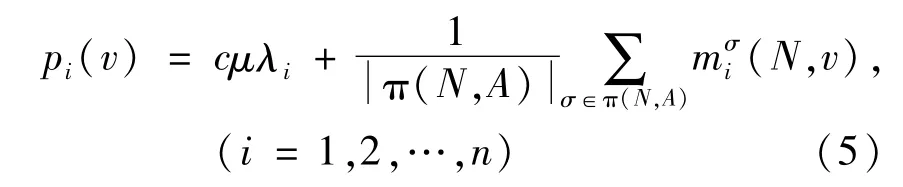
定理2 成本分摊规则p（v）＝（p1（v），p2（v），…，pn（v））是随机环境下零售商联合采购与合并运输合作博弈的一个核配置.

证明

（1）对于

（2）a.如果联合运输与采购联盟S中含有距供应商最远的零售商σ-1（1），则有，

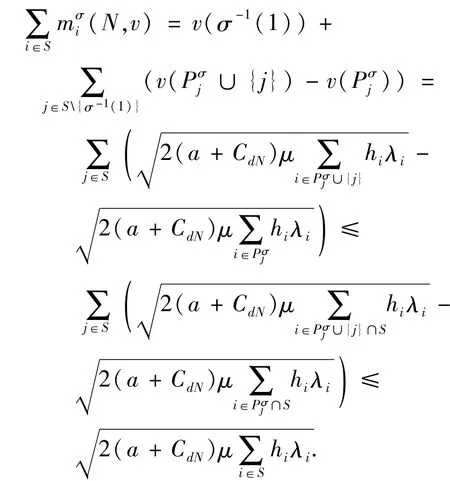
b.如果联合采购与运输联盟S中不包含距供应商最远的零售商σ-1（1）.则令（1）｝，可知，由合作博弈（N，v）的次可加性，有成立.因此，），从而则有也成立.

4 数值例子

本小节将通过一个实际案例，对本文所提出的成本分摊规则进行说明.假设所考虑的随机需求环境下联合采购与合并运输供应链中仅有3个零售商，分别为“全家”在广州大学城的3个超市，分别编号为1，2，3，据调研可知，他们每天会联合采购“怡宝”矿泉水并进行合并运输.设每家“全家”超市每天内的单数量为λi（i＝1，2，3），每一笔订单的平均需求量为μ，配送中心到超市的运输成本为Cdi（i＝1，2，3），而每一家超市的持有成本为hi（i＝1，2，3），统一的进货成本为c，3家超市的具体参数见表1.

表1 3个零售商的参数Table 1 Parameters of three retailers

通过表2可知，在表1所给出的参数下，随机需求环境下零售商联合采购与合并运输合作博弈满足次可加性，从而零售商之间进行合作是可以获益的.因此，表3则给出了零售商间形成不同合作联盟时的运作成本.

表2 联合采购与合并运输合作博弈的次可加性Table 2 Subadditivity of collaborative procurement and shipment consolidation game

表3 联合采购与合并运输联盟的运作成本Table 3 Operational cost of collaborative procurement and shipment consolidation coalitions

由系统给定的参数可知，π（N，A）＝｛（3，2，1）｝，根据pi（v）的计算公式可知，按分配规则p（v）所给出的成本分摊方案为：（60 898.4，37 740.4，31 959.6），该分配方案在联合采购与合并运输合作博弈的核中.

5 结 论

文章建立了随机需求环境下，零售商联合采购与合并运输联盟的合作博弈模型.首先，在随机到达的需求下得到了零售商进行联合采购与合并运输联盟的最优订货策略；随后，指出在随机环境下零售商的联合采购与合并运输战略并不一定能降低各自的成本，并给出了合作可以降低各自成本的条件（即满足次可加性的条件）；根据边际成本给出了可行的成本分摊规则，并证明了在此分摊规则下，可以保持大联盟的稳定，最后通过一个具体的实例对成本分摊方案进行了说明.

［1］ ESSIG M.Purchasing consortia as symbiotic relationships：Developing the concept of“consortium sourcing”［J］.Eur J Purch Supply Manag，2000，6（1）：13-22.

［2］ TELLA E，VIROLAINEN V M.Motives behind purchasing consortia［J］.Int J Prod Econ，2005，93：161-168.

［3］ HEIJBOER G.Mathematical and statistical analysis of initial purchasing decisions［D］.Enschede：University of Twente，2003.

［4］ DANA J.Buyer groups as strategic commitments［R］.Evanston：Kellogg School of Business Working Paper，Northwestern University，2004.

［5］ MECA A，TIMMER J，GARCÍA-JURADO I，et al.Inventory games［J］.Eur J Oper Res，2004：127-139.

［6］ MECA A，GARCÍA-JURADO I，BORM P.Cooperation and competition in inventory games［J］.Math Meth Oper Res，2003，57（3）：481-493.

［7］ MECA A，GUARDIOLA L A，TOLEDO A.P-Additive games：A class of totally balanced games arising from inventory situations with temporary discounts［J］.TOP，2007，15：322-340.

［8］ 肖旦，周永务.数量折扣契约下制造商与零售商库存合作联盟的稳定性［J］.运筹与管理，2013，22（2）：20-26，43.XIAO D，ZHOU Y W.Stability of the inventory coalitions of manufacturer and retailers under quantity discount contract［J］.Oper Res Manag Sci，2013，22（2）：20-26，43.

［9］ 肖旦，周永务，汤勤深.考虑次品率的零售商库存联盟订货量与稳定性分析［J］.工业工程，2013，16（3）：32-37.XIAO D，ZHOU Y W，TANG Q S.On stability of retailers′coalition for items with imperfect quality［J］.Ind Eng J，2013，16（3）：32-37.

［10］冯海荣，李军，曾银莲.易腐品供应链企业联合采购决策与费用分配研究［J］.系统科学与数学，2011，31（11）：1454-1466.FENG H R，LI J，ZENG Y L.Study on collaborative purchasing and cost allocation problem in supply chains with perishable products［J］.J Syst Sci Math Sci，2011，31（11）：1454-1466.

［11］冯海荣，李军，曾银莲.延期支付下的易腐品联合采购费用分配［J］.系统工程理论与实践，2013，33（6）：1411-1423.FENG H R，LI J，ZENG Y L.Cost allocation for collaborative procurement on perishable products under permissible delay in payments［J］.Syst Eng Theory Pract，2013，33（6）：1411-1423.

［12］FIESTRAS-JANEIRO M，GARCÍA-JURADO I，MECA A，et al.Cost allocation in inventory transportation systems［J］.TOP，2012，20（2）：397-410.

［13］曾银莲，李军，冯海荣.随机需求环境下零担货物运输合作［J］.管理科学学报，2015，18（7）：48-58.ZENG Y L，L J，FENG H R.Collaboration in less-than-truckload transportation with stochastic demand［J］.J Manag Sci China，2015，18（7）：48-58.

Stability of retailers’coalition w ith collaborative procurement and shipment consolidation under stochastic demand

XIAO Dan，LIU Fang，SHI Xin-xiang，Q IN Long-yi
（School of Business Administration，Guangzhou University，Guangzhou 510006，China）

In order to reduce operating cost，companies will form coalitions which adopt strategies of collaborative procurement and shipment consolidation under stochastic demand.However，they have to allocate the operational cost fairly and rationally to keep the stability of coalition.This paper uses cooperative game to analyze the stability of retailers'coalition with collaborative procurement and shipment consolidation under stochastic demand.First of all，we get the optimal order quantities of the coalition.Then，we show that the cooperation of purchasement and shipment will not always reduce the total operating costs，we give the conditions under which the cooperation will be better for all members.Lastly，we provide that a cost allocation rule for the case that follows from each retailer's marginal cost will keep the grand coalition stability.

stochastic demand；shipment consolidation；order quantity；stability

F 275

A

1671-4229（2016）01-0090-06

【责任编辑：孙向荣】

2015-11-02；

2015-12-02

广东省自然科学基金博士启动资助项目（2014A030310443，2015A030310192）；教育部人文社科项目一般资助项目（15YJC630138，15YJC630072）

肖旦（1986-），男，讲师.E-mail：danx2003＠hotmail.com.