凸显数学思想方法提升中职数学课品质——以“直线的倾斜角与斜率”为例
2016-11-25浙江省宁波市北仑职业高级中学乐志刚
☉浙江省宁波市北仑职业高级中学 乐志刚
凸显数学思想方法提升中职数学课品质——以“直线的倾斜角与斜率”为例
☉浙江省宁波市北仑职业高级中学乐志刚
数学思想方法教学一直被认为是改变数学教师观念、提高教师素质的主要途径.传授数学知识、演化数学思想、传承数学文化是数学教育的重要内容,从这个意义而言,掌握了数学方法就是掌握了课堂的要义,掌握了数学的精髓,从而也为学生的发展指明了一条光明的道路.在教学过程,教师如果能够注意渗透常见的数学思想方法,注意一些数学思想挖掘、提炼和渗透,这对中职学生的学习数学、培养能力、开发智力及提高学生的素质都是至关重要的.本文以高等教育出版社出版的中职《数学》基础模块下册中第八章第二节“直线的倾斜角与斜率”为例,浅议数学思想方法在教学中的渗透.
一、渗透建模思想,增强学生分析问题、理论联系实际的能力
教师应重视数学思想方法的教学,指导学生建立合适的数学模型进行数学分析.在解决实际问题时,对基础知识的具体应用,是指学生遇到数学问题,采取何种应对策略进行解决,该做什么及怎么做,这些都属于数学方法的范畴,至于做的好与坏,则可以归为数学思想的范畴了.
为了调动中职学生学习数学的情感与兴趣、启发学生的思维,帮助学生积极和主动地参与到数学课堂的活动中,我们往往采用“情景教学”.本节首要的任务是学习直线倾斜角的概念,如图1所示.在教学中,我们通过高射炮的图示导入,以地面所在直线为x轴、垂直地面所在直线为y轴、炮管中心轴为所在直线,为了确定直线对x轴的倾斜程度,引入直线倾斜角的概念.这就是通过生活中的实例图像向数学中的基本图形转变,从而使抽象的数学概念实物化,架起数学知识和实际问题之间的桥梁,灵活运用建模思想.
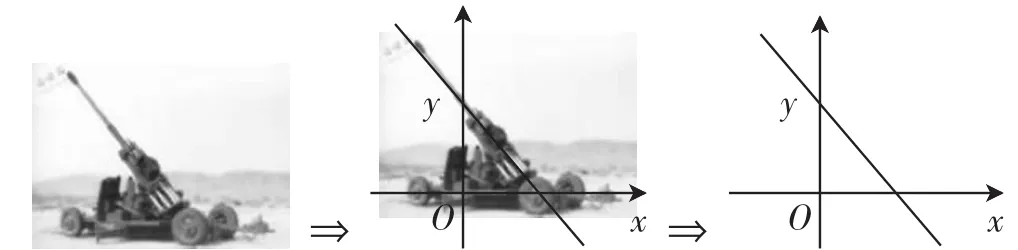
图1
二、渗透数形结合的思想方法,提高学生的数形转化能力和迁移能力
数形结合思想是学生形成数学意识的纽带,它很好地把几何内容和代数知识结合起来,是培养学生数学观念的载体.作为一种隐性的知识,数学结合思想具有隐喻性的特点,它隐于知识内部,又高于书本的知识.数形结合作为一种常见的数学思想方法在日常的教学中是非常实用和常见的,图形性质与数量关系之间形成互换是它的常见形态.
在实际情况下,高射炮的炮管是可以调节的,所以它的倾斜角是在变化.而在本节内容中,我们引导学生通过直线旋转,来寻找直线倾斜角的取值范围,观察倾斜角a与直线方程(一次函数y=kx+b的形式)中x的系数k之间的关系,这就是最简单数形结合思想的体现.结合直线旋转过程中产生的几种图形能有效地帮助学生找到直线倾斜角的取值范围并且形成直线斜率的概念.例如,在教学中,为了便于学生更好地理解直线斜率的概念,我们借助几何画板设计:(1)α变化→直线的变化→y= kx+b中x的系数k变化(同时观察tanα的变化);(2)y=kx+b中x的系数k变化→直线的变化→α变化(同时观察tanα的变化).通过动态演绎,数与形就结合起来了,这样,能够帮助学生更好地理解斜率这一数学概念,如图2所示.
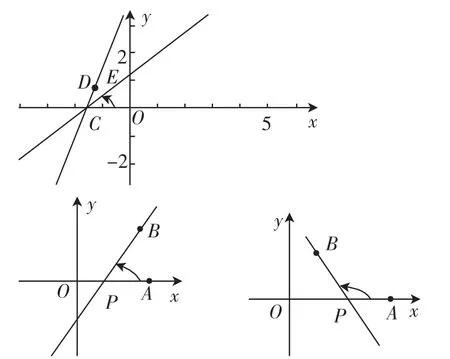
图2
三、渗透分类讨论思想,培养学生全面观察事物,灵活处理问题的能力
职高数学教学担负着培养学生理性思维的责任,数学教师一定要不断探索有效的教学方式,激发学生学习数学的兴趣.数学思想方法的培养可以将抽象的数量关系具体化,把无形的解题思路形象化,这样有利于培养学生解题的灵活性、多样性和变通性,对于发展学生的思维能力起着积极推动作用.
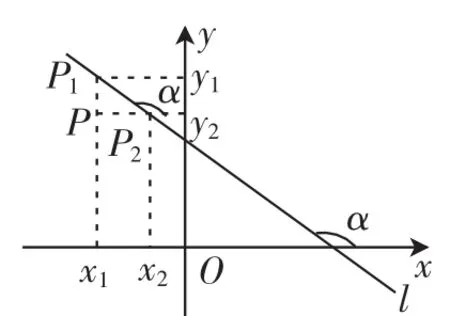
图3
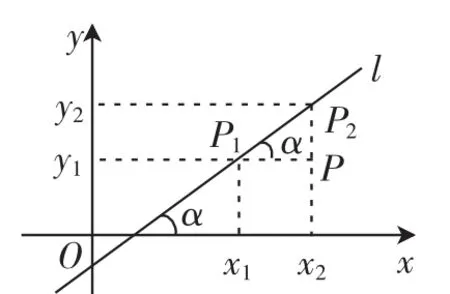
图4
例如,当我们研究如何根据直线上的任意两个点的坐标来确定倾角大小的时候,我们就要分两类情况来讨论:当α≠90°时,x1≠x2,tanα=(如图3、4);当α=90°时,x1=x2,tanα的值不存在,此时直线l与x轴垂直(如图5).前面通过学习,我们发现倾角α(α≠90°)的正切值叫作直线l的斜率,用小写字母k表示,即k=tanα.为了更加准确地理解斜率k和倾斜角α的关系,我们将k分为四种情况来确定倾斜角α的取值:当k<0时,90°<α<180°;当k=0时,α=0°;当k>0时,0°< α<90°;当k不存在时,α=90°.
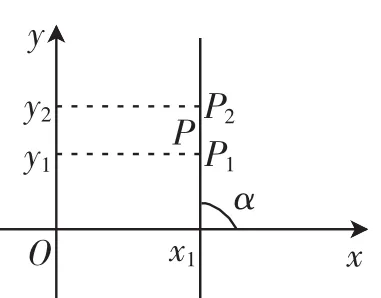
图5
四、渗透方程与函数的思想,巩固学生的计算能力

α 0° 30° 45° 60° 120° 135° 150° k
引导学生通过建立方程,形成模型思想,这是最基本、最常用的数学方法.在教学中,只有加强数学意识的教学,才能使学生得心应手,从容应答,从而突破思维的桎梏,达到理想的状态.
按照教学大纲要求,本节课需要中职学生掌握直线的倾斜角和斜率的计算方法.根据直线斜率和倾斜角的计算公式k=tanα(α≠90°),我们把倾斜角α看作自变量,斜率k看作α的函数,通过对应法则求相对应的值.同时,我们根据中职学生的特点,结合后面直线方程的知识点,我们将所有特殊角列出,结合方程的思想,要求学生求出相对应的斜率值,如下表:
五、渗透化归思想,提高学生解决问题的能力
化归是一种常见的数学思想方法,简单的说,如果一个难题直接解决存在一定的困难,我们就可以通过等价类比进行转化,通过转化成我们能够解决的问题或者形式来给予解决的方法,这是思想方法较高的层次,可以说化归思想在数学新教材中是贯穿始终的.
以本节内容为例,课后习题2:设点P(-3,1)、Q(-5,3),则直线PQ的斜率为_______,倾角为_______.这道题目就是直线的倾斜角、斜率及坐标之间的转换,相关计算方法tanα(α≠90°)=k=的综合.为了培养学生的化归思想,深化直线倾斜角和斜率的概念,提高部分学生继续探究的能力,我们提出习题:已知直线l1平行于直线l2,l1上任意两点A(-2,2)、B(3,-1),l2上任意两点C(4,2)、D(x,x+2),求点D坐标.引导学生从问题出发,在已知条件中寻找突破点,搭建解决问题的桥梁.接下来就是求出D点的坐标,然后依次求解出直线l2的斜率.根据初中所学的知识“两直线平行,同位角相等”,我们通过两直线平行的条件,了解到倾斜角是相同的,因此斜率也相同.借助于直线l1的两点坐标求出直线l1的斜率,最终解决点D的坐标.这就是化归思想在本节教学中的运用.
总之,数学中渗透着基本数学思想,它们是基础知识的灵魂和脊髓,是数学问题的本质反映,追求的是“授人以渔”,让学生掌握学习数学的“金钥匙”,是数学发展的杠杆.可以说,数学思想较之于数学基础知识及常用数学方法又处于更高层次,它来源于数学基础知识及常用的数学方法,在运用数学基础知识及方法处理数学问题时,具有指导性的地位.在日常教学中,教师应当把握数学知识的来龙去脉,把数学教学上升到思想方法的层次,才能有效激发学生学习数学的兴趣,展示数学发展的过程.
1.陈克胜.基于数学文化的数学课程再思考[J].数学教育学报,2009(1).
2.徐明华.从一节随堂课看数学文化教育的实施[J].中学数学教学参考(中),2010(7).
3.张德勤.数学思想方法的意义、分类与教学价值[J].教学研究与评论,2013(8).F
