基于稀疏表示的轴承早期故障特征提取
2016-11-25余发军周凤星严保康
余发军, 周凤星, 严保康
(1.武汉科技大学 信息科学与工程学院,湖北,武汉 430081;2.中原工学院 信息商务学院,河南,郑州 451191)
基于稀疏表示的轴承早期故障特征提取
余发军1,2, 周凤星1, 严保康1
(1.武汉科技大学 信息科学与工程学院,湖北,武汉 430081;2.中原工学院 信息商务学院,河南,郑州 451191)
低速重载机械设备中的滚动轴承由于承受巨大载荷,极易出现内外环故障. 在故障早期阶段,反映故障特征的冲击成分很微弱,极易被噪声覆盖而难以识别. 为准确诊断轴承早期故障,提出基于稀疏表示的故障特征提取方法. 该方法利用K-SVD字典训练算法构造出能准确匹配冲击成分的字典,克服了参数化字典缺乏自适应性的问题;稀疏编码过程中,采用批处理正交匹配追踪算法(batch orthogonal matching pursuit,Batch-OMP)对振动信号进行分解,以逼近信号的峭度值最大原则作为分解结束条件,自适应确定出分解次数;最后,通过对重构的特征成分进行包络谱分析得出故障类型. 对仿真信号和轴承振动信号进行故障特征提取,结果表明所提方法能准确提取出冲击成分,验证了其有效性和实用性.
稀疏表示;K-SVD;Batch-OMP;峭度值;冲击成分;轴承故障诊断
低速重载机械设备中,滚动轴承承受巨大的载荷,是整个设备中极易发生故障的部件,常以内环、外环和滚动体等故障类型为主. 正常工作状态下的轴承,将转轴与轴座之间滑动摩擦转化为滚动摩擦,转轴旋转均匀;出现早期故障时,转轴的旋转将会抖动和不均匀,如果此时不能识别并更换轴承,故障点将迅速加深和扩大,使整个设备陷入瘫痪状态,甚至造成巨大灾害[1]. 因此,进行轴承早期故障监测和诊断对保障整个低速重载机械设备的正常运行至关重要. 测取振动信号并进行故障特征提取是轴承故障诊断的常用方法[2],然而,设备在运转过程中,转速和工况经常发生变化,因此测取的振动信号具有非平稳性;另一方面早期故障的特征成分很微弱,极易被噪声覆盖,因此很难直接从时域或频域判断故障的类型[3]. 近年来,小波分析和EEMD方法等被多次应用到机械故障特征提取中,取得了一定效果,但小波分析受小波基和分解尺度影响较大,而EEMD的抗混效果受白噪声幅值系数和总体平均次数等参数影响较大[4].
稀疏表示方法利用稀疏分解算法将信号表示成少量原子的线性组合[5],是分析非平稳信号的有力工具,在一定程度上克服了小波变换和EEMD的缺陷,已在信号去噪、图像压缩编码、数学建模等领域得到了广泛的应用. 目前,已有多个文献将信号稀疏表示应用到机械故障诊断领域. 这些文献可以归为两大类:一类直接利用稀疏分解思想(如基追踪、匹配追踪等算法)进行故障特征提取,另一类利用稀疏理论的延伸方法(如形态稀疏、稀疏盲分离等方法)进行故障特征分离. 直接利用稀疏分解思想如:严保康等[6-7]先构造预定义的冗余字典,再利用某种优化算法对滚动轴承的故障特征成分进行匹配追踪(MP)或分段正交匹配追踪(StOMP). 利用稀疏理论的延伸方法如:陈向民等[8]通过构造形态不同的冗余字典对齿轮箱复合故障进行形态分离;李豫川等[9]通过形态滤波和稀疏分量分析原理对滚动轴承故障盲分离. 尽管这两大类方法在各自应用中都能提取出故障特征成分,但由于事先预定义的字典缺乏对故障特征的自适应能力,因此应用在复杂工况下低速重载机械故障识别时难以奏效.
为了准确提取低速重载机械中轴承的早期故障特征,采用基于字典学习的稀疏表示方法对故障进行特征提取. 字典学习,是以样本信号集为模板利用机器学习算法对其进行训练的一种字典构造方法. 最优方向法[10](method of optimal directions, MOD)、K均值奇异值分解法[11](K-SVD)是两种常用的字典学习算法. 其中K-SVD具有理论成熟、匹配精度高等优点,已被成功应用到多个领域,本文拟采用K-SVD字典学习算法构造自适应字典以提高匹配精度. 另一方面,特征稀疏提取过程中,分解结束条件是个难点问题. 若待分解信号只包含故障特征成分和白噪声,则通常将信号分解的残差与某个阈值进行比较,小于阈值则分解结束,这就要求阈值设置尽可能接近噪声功率. 但实际应用中,噪声功率难以估计,因此,本文在稀疏分解过程中引入峭度值最大原则,每次分解后计算逼近信号的峭度值,当峭度达到最大时,分解结束. 通过仿真测试和轴承实验验证,所提方法能自适应的构造匹配字典,与参数化的字典相比,提取的冲击成分更准确,为低速重载机械中的轴承早期故障诊断提供了一种有效方法.
1 特征提取模型
假设采集的振动信号为y,其中包含故障特征成分x和高斯白噪声v
(1)
式中x,y,v∈RN.
根据稀疏表示理论,y可以在过完备字典
上表示为
(2)
式中:ε为信号的残差;〈,〉表示内积运算. 信号在稀疏分解过程中,由于故障特征成分x具有一定的结构特征,所以与原子库具有较强的相关性,投影系数较大,仅由少量原子线性组合即可较好逼近;而高斯白噪声v是随机分布的,不具有一定的结构特征,所以与原子库表现弱相关性,投影系数较小,需要较多原子才能较好逼近[12]. 由以上分析可知,当将振动信号y在一个过完备字典上用匹配追踪算法进行稀疏分解时,其中的故障特征成分x首先得到分解,而噪声v最后才得到分解. 如果能找到判别分解x和v的分界点依据,并以此作为稀疏分解迭代的终止条件,那么就可有效将特征成分x从测量信号y中提取出来.
峭度作为一种时域统计量,是描述波形尖峰程度的参数[13],其定义为
(3)
式中:E( )表示求均值;σ和μ分别为信号x的标准差和均值. 由文献[13]可知,正常轴承振动信号服从正态分布,其峭度值约为3;发生故障时,其振动信号中的瞬态冲击成分对峭度值影响非常显著,使其值明显大于3,谐波成分的峭度值明显小于3. 将机械系统振动信号经过稀疏分解后,得到各迭代次数的逼近信号,根据它们的峭度值判断该次分解是否含有噪声成分,可以给故障诊断带来帮助. 将其引入到稀疏分解迭代终止条件中,可以表示成
(4)
式中:K( )表示求峭度;λ为惩罚因子;Γ为稀疏度. 由式(4)可以看出,在稀疏分解过程中需要计算每次迭代后逼近信号的峭度值,直到峭度达到最大时,迭代结束.
2 稀疏特征提取的步骤
2.1 自适应字典的构造
当构造的字典包含了信号的结构特征时,才能获得信号的稀疏表示. 采用参数化的字典或多个原子库的级联构造字典时,原子的数量较大,稀疏表示运算量会很大,而且当被分解信号改变时,需构造相应更多的原子,缺乏自适应信号的能力. 为了得到包含信号结构特征的自适应字典,本文采用K-SVD字典学习算法,以原始测量振动信号作为学习样本,利用稀疏表示-字典更新两步法循环迭代实现自适应字典的构造. 假设原始测量振动信号y的长度为N,将其按一定的重叠率分割成m个样本,每个样本的长度都为n(n< Y=[y1y2… ym]∈Rn×m. 利用K-SVD算法训练字典,使目标函数为 (5) 式中W=[w1w2…wm]为yi的稀疏表示系数. 式(5)的优化问题,用以下几个步骤解决: ① 利用随机数初始化字典D,使其每个原子具有单位2-范数; ② 采用正交匹配追踪稀疏分解算法,求得样本Y的系数矩阵W; ③ 固定系数矩阵W,利用奇异值分解逐个更新每个原子,使逼近误差最小; ④ 重复步骤②③,直到达到预定的迭代次数结束. 2.2 稀疏系数的求取 (6) 2.3 特征成分的提取 (7) 式(7)是二次项优化问题,可以转化成 (8) 总结所提方法提取轴承早期故障特征成分的步骤: ① 将轴承振动信号按一定规则重叠分割成m个样本,用K-SVD字典训练算法构造自适应字典D; 仿真信号包含周期冲击成分和噪声成分. 其中:每个周期内冲击函数为exp(-100t)×cos(300πt),重复的频率为10 Hz;叠加不同强度的高斯白噪声,分别得到信噪比为-1,0,1,3和6 dB的混合信号. 采样频率为1 000 Hz,采样点为1 000. 分别用基于Gabor字典MP(使用遗传算法进行优化)方法(简称Gabor-MP方法)和本文方法对相同信噪比的仿真信号进行提取,比较两者效果. 实施本文方法时:在字典学习阶段,将仿真信号按步长为2和3交替重叠方式分成400个样本,每个样本的长度为8,字典的大小为256,训练次数为20;在稀疏表示阶段,将仿真信号重叠分割成8个批,批的长度为258,再将每个批按步长为2重叠抽样成块矩阵,使块矩阵的大小为8×126. 实施Gabor-MP方法和本文方法后,提取的特征成分的噪声水平和峭度值分别如图1(a)、1(b)所示. 由图1可以看出,在不同的信噪比下,尤其在故障早期的-1 dB和0 dB的低信噪比下,本文方法比Gabor-MP方法能更好地提取出周期冲击成分,使其所含的噪声水平更低,峭度值也具有更明显的优势. 图2显示了仿真信号的信噪比为0 dB时两种方法的处理结果,从图2(b)可以看出,图2(a)中周期冲击成分被噪声覆盖,难以识别,经两种方法处理后(如图2(c)和图2(d)所示),周期的冲击成分都显现了出来,但本文方法提取的冲击成分的波形更接近于原始波形,失真更小. 为了验证峭度在Batch-OMP稀疏分解过程的有效性,考察第一个批的稀疏逼近信号峭度随迭代次数的关系,随着迭代次数的增加,逼近信号的峭度先增加后减小;在第3次迭代时峭度达到了最大15.64. 计算迭代次数为2,3,4时逼近信号与原始冲击成分(前258点)的均方差,三者分别为0.027 45,0.018 96和0.030 12,由此可以看出,用峭度最大原则作为稀疏分解迭代终止条件是有效的. 为进一步验证所提方法的有效性,用旋转机械振动故障试验平台模拟低速重载机械中轴承早期故障. 该试验平台主要由调速电机、传动轴、轴承支架、模拟负载和数据采集等部分组成,其中数据采集部分由压电加速度传感器和信号采集器完成. 实验中,轴承的型号为N205EM(外径为52 mm,内径为25 mm,滚动体数为12,滚动体直径为7.5 mm,接触角为0°),分别在轴承的内外环上用激光切割一个微小凹点故障以模拟故障早期特征,电机运行转速设置较低速的300 r/min,加载较大负载以模拟低速重载工况,数据采集频率为20 kHz. 根据故障特征频率计算公式可以计算出内环故障特征频率fi=35.7 Hz,外环故障特征频率fo=24.3 Hz. 分别用Gabor-MP方法和本文方法对两种故障类型的振动数据进行特征提取. 图3(a)内环故障类型的振动信号波形中,由于振动源(内环)与传感器安装位置(采集点)有一定传播距离,所以冲击成分幅值较小且不明显,几乎淹没在噪声里,直接难以识别故障的类型. 两种方法处理后(如图3(b)和3(c)所示),冲击成分显现了出来. 由于压电式加速度传感器安装位置的原因,当内环的故障点转动到安装点附近时,表现出相应的位置处脉冲幅值较大,而当故障点偏离安装点一定距离时,脉冲幅值有所减小,所以冲击成分的幅值表现出受到转频调制的现象,这一现象当轴承处于低速重载运行状态时表现的更加突出. 虽然两种方法都能提取出冲击成分,但本文方法效果更加明显,对本文方法提取的冲击成分进行包络谱分析(如图4所示),转频5 Hz及其倍频、故障特征频率36.0 Hz及其与转频的上下差频非常突出,其中的36.0 Hz特征频率与理论计算的内环故障特征频率35.7 Hz非常接近,由此可以判断该轴承存在内环故障,与实际加工的故障情况相符. 图5(a)显示了轴承外环故障的振动数据的波形,由于振动源(外环)与传感器安装位置(采集点)的传播距离较近,所以冲击成分的幅值较大,但波形中仍然含有一定强度的噪声. 用两种方法对其进行特征提取(如图5(b)和5(c)所示),冲击成分更加突出显著,且其幅值大小几乎相等,说明没有受到转频的调制,这主要由于轴承外环固定,故障点相对于压电式加速度传感器安装点的距离是固定的,不管转动到一圈中的什么位置,振动源与采集点传播距离是固定的,所以冲击成分是等幅的. 对本文方法提取的特征成分进行包络谱分析(如图6所示),24.2 Hz及其倍频非常明显,与理论计算的外环故障特征频率24.3 Hz非常接近,由此可以判断该轴承存在外环故障,与实际加工的故障情况相符. ① 提出了一种基于字典学习的轴承早期故障稀疏特征提取方法,该方法利用K-SVD字典学习算法构造能准确匹配特征成分的字典,在稀疏分解过程中,通过计算每次迭代后逼近信号的峭度值,利用峭度是否达到最大作为迭代终止条件,能自适应的确定出特征成分与噪声成分的稀疏表示分解点. 通过与参数化的字典相比,基于字典学习的稀疏特征提取方法能使提取的冲击波形更接近其本来的波形,失真更小. ② 通过模拟低速重载工况的轴承内外环故障实验发现:内环故障时,由于振动源与传感器采集点较远,其故障特征成分幅值很微弱. 在强噪声背景下,本文方法能准确识别冲击出现的位置和幅度的变化情况,基于参数化的Gabor-MP方法提取的冲击成分难以准确显示出幅度变化情况,而内环故障识别的重要依据就是冲击出现间隔和幅度调制情况,所以本文方法相对于参数化的Gabor-MP方法有较明显的优势;外环故障时,两种方法都能准确识别冲击出现的位置,但本文方法提取的结果所含噪声更小,其幅值情况也更接近相等,这点与外环故障特征的等幅特性相一致,因此,所提方法可以为低转速下的重载机械轴承早期故障诊断提供依据. [1] 陈向民.基于形态分量分析和线调频小波路径追踪的机械故障诊断方法研究[D].长沙:湖南大学,2013. Chen Xiangmin. Research on fault diagnosis methods for machinery based on morphological component analysis and chirplet path pursuit [D]. Changsha: Hunan University, 2013.(in Chinese) [2] 李兆飞.振动故障分形特征提取及诊断方法研究[D].重庆:重庆大学,2013 . Li Zhaofei. Study on vibration signal based fractal feature extraction methods for fault diagnosis[D]. Chongqing: Chongqing University, 2013. (in Chinese) [3] 王宏超,陈进,董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报,2013,49(1):88-94. Wang Hongchao, Chen Jin, Dong Guangming. Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition[J]. Journal of Mechanical Engineer, 2013,49(1):88-94.(in Chinese) [4] 陈仁祥,汤宝平,杨黎霞,等.自适应参数优化EEMD机械故障特征提取方法[J].振动,测试与诊断,2014,34(6):1065-1071. Chen Renxiang, Tang Baoping, Yang Lixia, et al. An EEMD feature extraction method of mechanical fault based on adaptive parameter optimum[J]. Journal of Vibration, Measurement & Diagnosis, 2014,34(6):1065-1071. (in Chinese) [5] Mallat S G, Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993,41(12):3397-3415. [6] 严保康,周凤星.基于相干累积量正交匹配追踪算法的轴承早期故障稀疏特征提取[J].机械工程学报,2014,50(13):88-94. Yan Baokang, Zhou Fengxing. Initial fault identification of bearing based on coherent cumulant stagewise orthogonal matching pursuit[J]. Journal of Mechanical Engineer, 2014,50(13):88-94. (in Chinese) [7] Cui Lingli, Wang Jing, Lee Seungchul. Matching pursuit of an adaptive impulse dictionary for bearing fault diagnosis[J]. Journal of Sound and Vibration, 2014(333):2840-2862. [8] 陈向民,于德介,李蓉.齿轮箱复合故障振动信号的形态分量分析[J].机械工程学报,2014,50(3):108-114. Chen Xiangmin, Yu Dejie, Li Rong. Analysis of gearbox compound fault vibration signal using morphological component analysis[J]. Journal of Mechanical Engineer, 2014,50(3):108-114. (in Chinese)[9] 李豫川,伍星,迟毅林,等.基于形态滤波和稀疏分量分析的滚动轴承故障盲分离[J].振动与冲击,2011,30(12):170-174. Li Yuchuan, Wu Xing, Chi Yilin, et al. Blind separation for rolling bearing faults based on morphological filtering and sparse component analysis[J]. Journal of Vibration and Shock, 2011,30(12):170-174. (in Chinese) [10] Engan K, Aase S O, Hakon Husoy J. Method of optimal directions for frame design[C]∥Proceedings ICASSP’ 99-IEEE International Conference on Acoustics, Speech, and Signal Processing. [S.l.]: IEEE, 1999:2443-2446. [11] Aharon M, Elad M, Bruckstein A M. The K-SVD: an algorithm for designing of over-complete dictionaries for sparse representation[J]. IEEE Transaction on Signal Processing, 2006,54(11):4311-4322. [12] 王国栋,阳建宏,黎敏,等.基于自适应稀疏表示的宽带噪声去除算法[J].仪器仪表学报,2011,32(8):1818-1823. Wang Guodong, Yang Jianhong, Li Min, et al. Wideband noise removing algorithm based on adaptive sparse representation[J]. Chinese Journal of Scientific Instrument, 2011,32(8):1818-1823. (in Chinese) [13] 丁康,黄志东,林慧斌.一种谱峭度和Morlet小波的滚动轴承微弱故障诊断方法[J].振动工程学报,2014,27(1):128-134. Ding Kang,Huang Zhidong, Lin Huibin. A weak fault diagnosis method for rolling element bearings based on Morlet wavelet and spectral kurtosis[J]. Journal of Vibration Engineering, 2014,27(1):128-134. (in Chinese) [14] Rubinstein R, Zibulevsky M, Elad M. Efficient implementation of the K-SVD Algorithm using batch orthogonal matching pursuit[J]. CS Technion, 2008,40(8):1-15. (责任编辑:李兵) Initial Fault Feature Extraction of Bearing Based on Sparse Representation YU Fa-jun1,2, ZHOU Feng-xing1, YAN Bao-kang1 (1.College of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan,Hubei 430081, China; 2.College of Information and Business, Zhongyuan University of Technology,Zhengzhou, He’nan 451191, China) Rolling bearings of low-speed and heavy-duty machinery work under huge load, therefore they are easily gotten inner or outer race faults. In initial fault stage, the impulse component, reflecting the fault feature in vibration signal, is difficult to extract for it is relatively weak and easily corrupted by strong background noise. A fault feature extraction method based on sparse representation was proposed to accurately diagnose the initial fault of bearing. The method utilized K-SVD dictionary training algorithm for constructing an accurate dictionary to match the impulse component and overcome the problem of parameter dictionary lack of adaptability. In sparse coding, batch orthogonal matching pursuit (Batch-OMP) algorithm was employed to sparse-decompose the vibration signal, and the kurtosis maximum principle of approximation signal was the end condition of decomposition, which determined the decomposition times adaptively. Finally, the feature component was reconstructed and its envelope spectrum was analyzed to diagnose the fault type. The fault feature was extracted by the proposed method from simulate and bearing vibration signals. The results show that the method can extract the impulse components accurately, which demonstrates its effectiveness and practicability. sparse representation; K-SVD; Batch-OMP; kurtosis value; impulse component; bearing fault diagnosis 2014-12-24 国家自然科学基金资助项目(61174106) 余发军(1981—),男,博士生,E-mail:524663102@qq.com. 周凤星(1952—),男,教授,博士生导师,E-mail:blackghostpeter@163.com. TN 911; TH 17 A 1001-0645(2016)04-0376-07 10.15918/j.tbit1001-0645.2016.04.008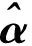
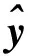
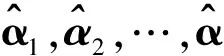
3 仿真测试
4 实验测试
5 结 论
